南海北部次表层叶绿素最大值年际变化特征分析*

王仁政, 单正垛, 孟思雨, 宫响

1. 青岛科技大学数理学院, 山东 青岛 266061;

2. 中国海洋大学环境科学与工程学院, 山东 青岛 266100

次表层叶绿素最大值(subsurface chlorophyll maxima, SCMs)是全球海洋生物剖面的显著共性之一,是层化水体中叶绿素浓度最大值发生在次表层的一种现象。在热带、亚热带海域SCMs 所贡献的初级生产力约占水体总初级生产力的30%～70%(Takahashi et al, 1984), 并且对海洋新生产力也有很大贡献。Hodges 等(2004)研究发现在SCMs 发生条件下新生产力的f比(新生产力在总初级生产力中的比例)增大了一倍, Hanson 等(2007)在澳大利亚附近寡营养海域发现这一最大值层中f比约为7%～32%。而海洋新生产力反映了海洋真光层对大气中CO2的净吸收能力。因此研究SCMs 现象, 特别是其年际变化对深入理解海洋生态系统在气候调节中的作用具有重要意义。

中国南海北部海域拥有十分复杂的环流体系、生态系统和水文特征(乐凤凤 等, 2006), 导致南海北部海域次表层叶绿素时空分布特征的多样性。众多学者开展了南海北部叶绿素垂直分布的研究, 如,张钒 等(2000)基于观测数据分析了1997 年8 月台湾海峡南部SCMs 特征因子的周日变化; 柯志新等(2013)研究了2008 年8、9 月份南海北部SCMs 的空间分布特征及其影响因素; Lu 等(2010)模拟研究了南海北部夏季SCMs 深度、强度与上升流、生物平衡的关系; Gong 等(2014)基于数值模拟研究了南海北部海盆区SCMs 的季节变化。

尽管对南海北部海域SCMs 现象已有一定认识,但由于现场观测数据不足且SCMs 发生在遥感可探测深度以外, 目前对SCMs 年际变化的研究较少。数值模拟是研究SCMs 的重要工具。本文采用一维物理—生态耦合模型模拟南海北部海盆区1994—2019 年海温、盐度、叶绿素等要素, 并基于模型结果, 采用3 种统计方法(创新趋势分析、经验模态分解和Mann-Kendall 突变检验)分别给出总体趋势、不同时间尺度变化过程及突变节点, 探讨了海水温度与SCMs 特征因子的关系及影响机制, 最后利用时间序列模型对2020 年3—11 月SCMs 特征因子的变化趋势进行预测。

1 数据和方法

1.1 数值模拟模型

本文采用的数值模型为一维物理-生态耦合模型(Modular Ecosystem Model-1D, MEM-1D)(Ricci et al, 2000)。生态模式采用的是欧洲区域性海洋生态系统模型(European Regional Sea Ecosystem Model,ERSEM), 详细过程见图1; 该模型已被成功应用于我国黄海与南海北部海洋生态系统的研究中(张冲等, 2011; Gong et al, 2014; Butenschön et al, 2016;Pan et al, 2017)。

图1 European Regional Sea Ecosystem Model 食物网结构Fig. 1 Schematic of the trophic structure of European Regional Sea Ecosystem Model

物理模式采用的是一维普林斯顿海洋模型(Princeton Ocean Model, POM), 其中湍混合模型采用传统的 2 阶 Mellor 和 Yamada 湍流闭合模型(Mellor et al, 1982), 并采用夏洁等(2006)研究中关于POM 模式的垂直涡动动量Kh和热混合系数Km的改进方案, 见公式1、2。

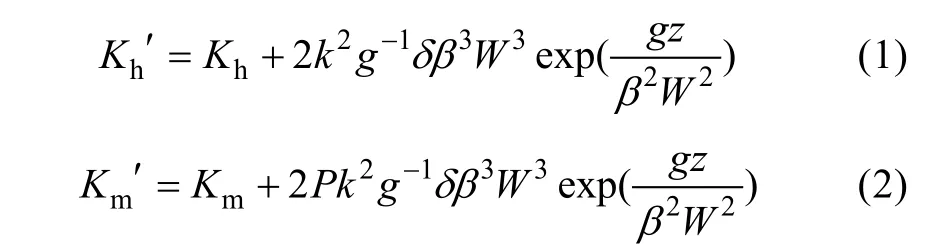
式中:W为风速;k为卡曼常数, 取0.4;δ为波陡, 取0.1;β为波龄, 取1.0; 重力加速度g取9.8m·s-2;P为与Richardson 数有关的无量纲系数, 取0.1;Z为水深;Kh′、Km′为考虑海浪作用后的垂直混合系数。

模拟区域为南海北部海盆区(南海18°N 以北且水深大于1000m 的区域)。模型水深取南海的平均深度1200m, 垂直方向上划分为上密下疏的40 层。时间步长为216s。模型模拟时间为1990—2019 年(其中1990—1993 年为模型spin-up 时间)。模型采用南海北部SEATS(South East Asian Time-series Study)站(18°N, 116°E)的温度、盐度、营养盐浓度和叶绿素浓度多年平均观测数据作为初始条件, 外强迫主要考虑风与太阳辐射, 均采用 SEATS 站附近1990—2019 年数据, 其中海表风速、净长波辐射通量与净短波辐射通量来自NCEP 再分析数据集, 潜热通量与显热通量通过COARE 算法(Fairall et al,1996)计算得到。本文模型参数主要来自ERSEM 中的常用参数, 部分选自南海及邻近海域的研究结果,具体参数见表1—4。

表1 ERSEM 模型基本参数的取值Tab. 1 Values of basic parameters of ERSEM model

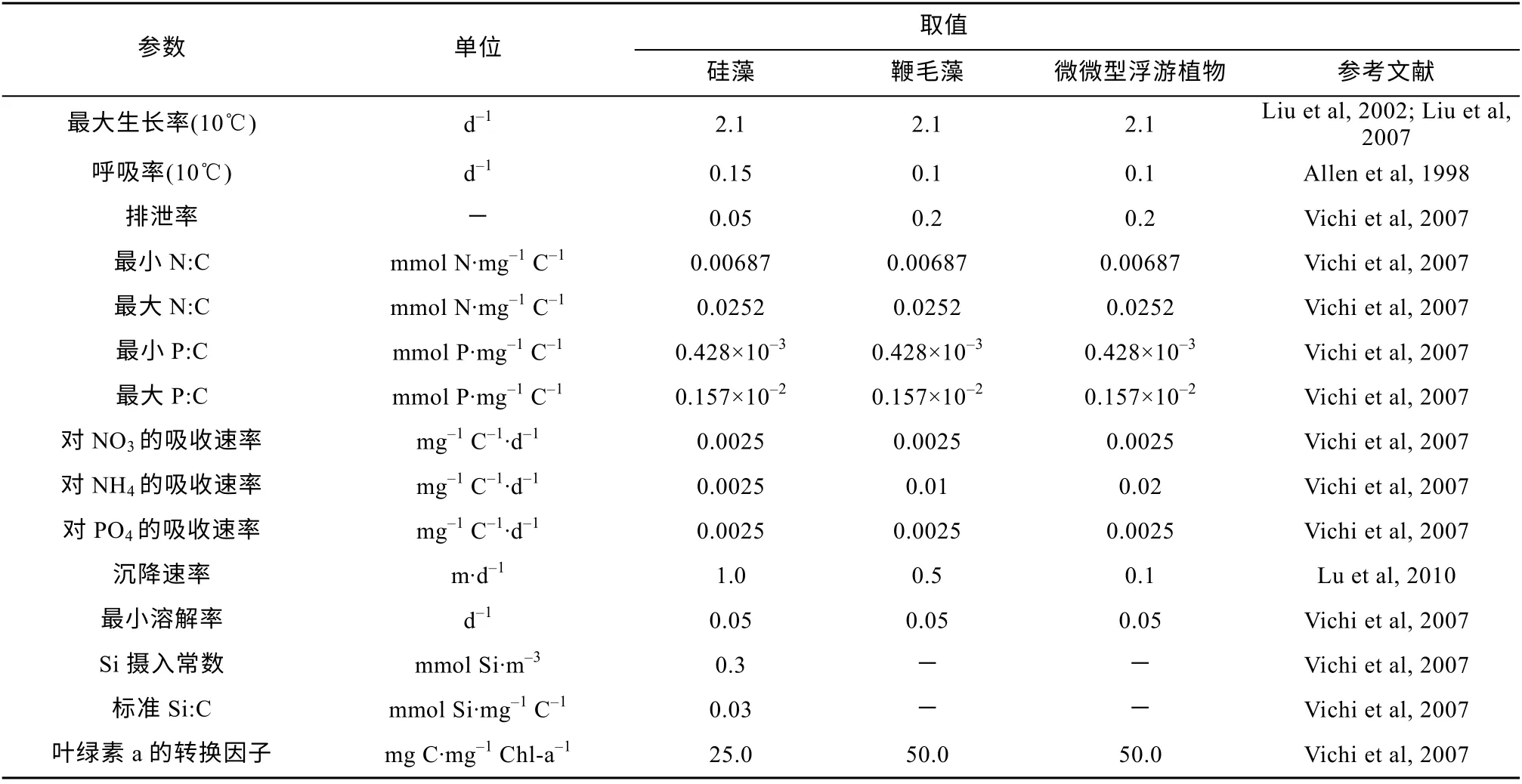
表2 浮游植物参数的取值Tab. 2 Values of phytoplankton parameters

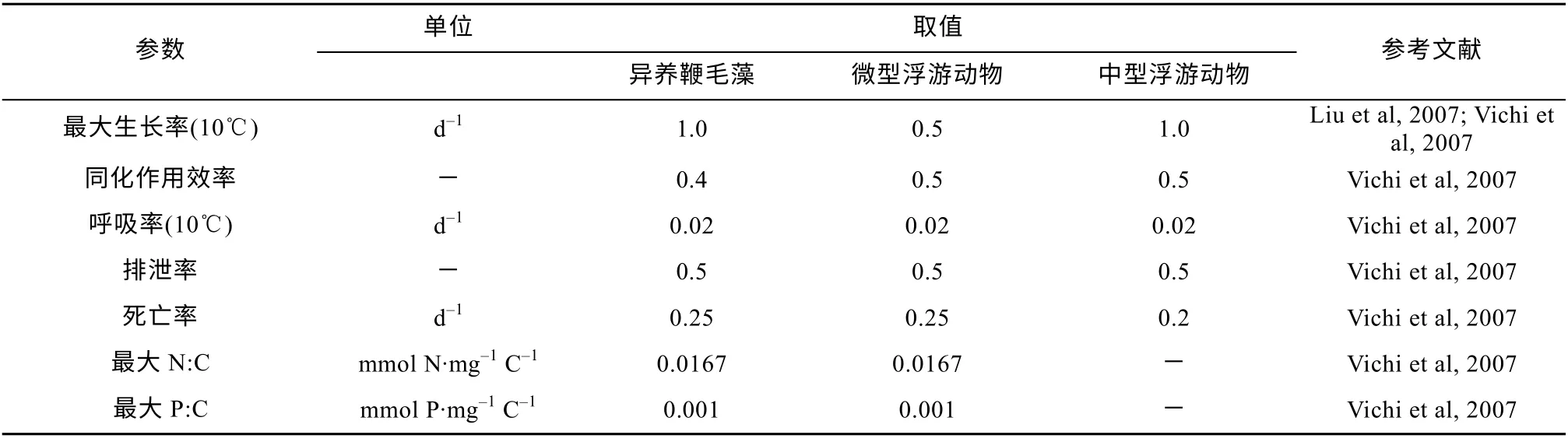
表3 浮游动物参数的取值Tab. 3 Values of zooplankton parameters

表4 细菌和碎屑参数的取值Tab. 4 Values of bacteria and debris parameters

1.2 统计方法

本文采用多种统计方法, 从不同角度分析SCMs 特征因子的年际变化特征。

1) 创新趋势分析(innovative trend analysis, ITA)是Şen(2012)提出的一种新型趋势检验方法。该方法的步骤为: 将一个时间序列等分为第一、第二两个子序列(若序列长度为奇数, 等分时不考虑第一项),将各子序列按照升序排列后将其分别放置于笛卡尔坐标系x,y轴, 通过观察数据点在1∶1 线附近的分布来判断数据趋势。趋势斜率nx可用于判断变化趋势, ITA 指数D(Wu et al, 2017)可用于判断趋势变化幅度(计算如式3)。

2) 经验模态分解(empirical mode decomposition,EMD)由Huang 等(1998)提出, 被广泛应用于趋势项提取、海洋数据分析(姜浩 等, 2018)、降雨量时间序列分析(陈国鼎 等, 2018)等问题。该方法的实质是不断地从数据中分解出高频分量, 并把剩下的低频分量作为新数据继续分解的过程。被分解出的高频分量被称作本征模态函数(intrinsic mode function,IMF), 其包含了原数据在不同时间尺度上的局部特征, 而最后无法继续分解的数据被称为残差(residual, RES), 通常情况下代表原始时间序列数据的趋势项。原始时间序列数据x(n) 可以表示为:

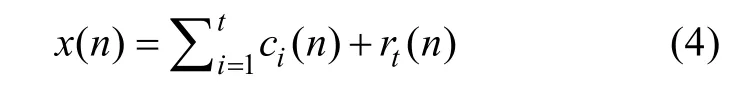
式中ci(n)为数据在第i时间尺度上的本征模态函数(IMF),rt(n) 为数据分解后的残差(RES)。

对于各不同时间尺度的本征模态函数, 其变化周期T可通过计算 IMF 平均频率ω(式 5)求得(Flandrin et al, 2004)。

式中:N为IMF 分量与x轴交点个数,L为第一交点与最后交点之间的距离。T为ω的倒数。

3) Mann-Kendall(M-K)突变检验是世界气象组织推荐并已被广泛使用的时间序列分析方法, 可以用于判断气候序列中是否存在气候突变, 如果存在,可确定出突变发生的时间。Mann-Kendall 检验法也经常用于气候变化影响下的降水、干旱频次趋势检测。该方法最初由H. B. Mann 和M. G. Kendall 提出(Mann, 1945; Kendall, 1975), 其原理为: 对于时间序列数据xn, 构造一个秩序列ri(i=2,3,…,n-1), 定义ri为: 针对xi所有满足j≤i且xj＜xi的数据xj的个数, 由此定义统计量Sk:

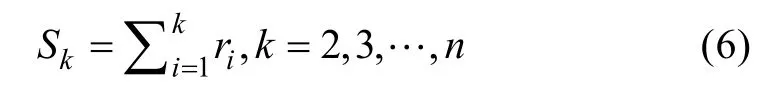
在满足时间序列独立且随机的前提下定义统计量(式7), 再将原序列数据逆序重新排列, 重复上述步骤构建新统计量。当时间序列为正序时, 统计量用UFk表示; 逆序时用UBk表示。根据UFk和UBk绘图曲线来判断数据趋势变化与突变点

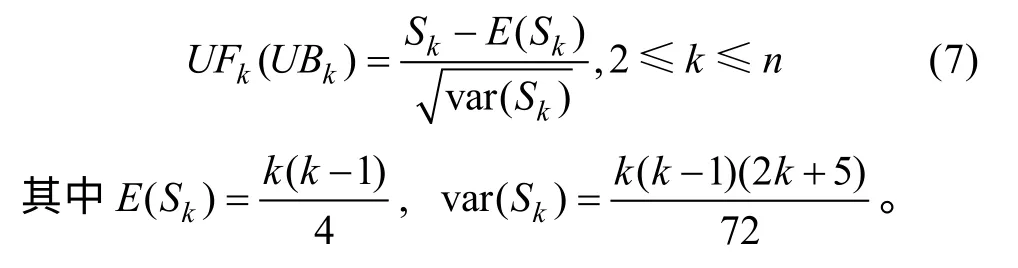
1.3 时间序列模型

差分整合移动平均自回归(auto regressive integrated moving average, ARIMA)模型是由Box 等(1970)提出的一种随机时间序列预测分析方法。该方法利用外推机制描述时间序列的变化, 是最小方差意义下一种精度较高的时序短期预测方法。为了处理具有周期性或季节性时间序列数据, 在ARIMA 模型的基础上拓展出了季节性差分自回归滑动平均(seasonal autoregressive integrated moving average, SARIMA)模型(Box 等, 1970)。SARIMA 模型是在假定季节相关和普通相关的交互作用下建立的乘法模型, 可以表示为SARIMA(p,d,q)×(P,D,Q)s。 模型一般形式如下式:

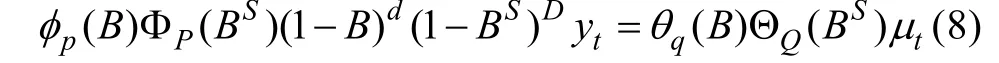
式中yt为时间序列,μt为随机项;φp(B)、ΦP(BS)分别为非季节与季节的自回归部分; (1-B)d、(1-Bs)D分别为非季节与季节的差分部分;θq(B)、ΘQ(BS)分别为非季节与季节的移动平均部分。

1.4 SCMs 特征因子定义

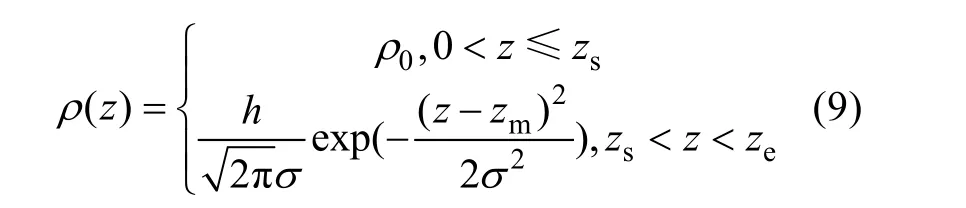
Lewis 等(1983)最早提出了通过高斯函数拟合将海洋中叶绿素浓度垂直分布数据参数化的方法,这为SCMs 的解析计算奠定了理论基础。由于上混合层内叶绿素垂直分布较为均匀, 而SCMs 多发生在上混合层以深, 本文采用分段函数拟合真光层中叶绿素浓度ρ的垂直分布(Gong et al, 2014):式中h是叶绿素浓度在区间[zs,ze]的垂直积分值,z代表水深(非负值),zs与0ρ均为常数, 分别为叶绿素浓度均匀分布处的最大水深和叶绿素浓度,σ为高斯分布的标准差,ze为真光层深度。SCMs 深度定义为叶绿素浓度最大值所处水深(zm)。SCMs 强度为次表层叶绿素浓度最大值(h/σ)。SCMs 厚度为SCMs 上下边界(满足 ∂2ρ(z)/∂z2= 0条件处)之间的水深(一般情况下为2σ, 当上混合层深度低于上边界时, 计算时需减去两者之间的差值)。

1.5 数据来源

2 结果与讨论

2.1 模型验证

为了验证MEM-1D 模型, 将模拟结果与南海SEATS 站观测数据进行比较(如图2—4)。基于南海北部海域冬季SCMs 现象不明显, 本文不分析南海北部12 月、1 月和2 月的SCMs 情况。

由图2、3 可知, 温度和盐度的模拟数据整体与观测数据较为吻合, 偏差主要集中在表层盐度, 这可能与所用模式没有考虑海表输入有关。MEM-1D模式较好地再现了南海北部海盆区的SCMs 现象(图4), 反映了SCMs 的季节变化和不同年份间差异, 特别是SCMs 深度与实际基本一致, 主要位于60～80m范围内。但模式对SCMs 强度的模拟存在一定偏差,如2000 年7 月和10 月SCMs 强度较实际偏小约0.15mg·m-3, 而 2004 年春季则略偏大, 这可能与SCMs 在不同站位的差异有关。本文所采用的分段函数能有效拟合上混合层以深的叶绿素垂直分布(图4), 得到SCMs 特征值。

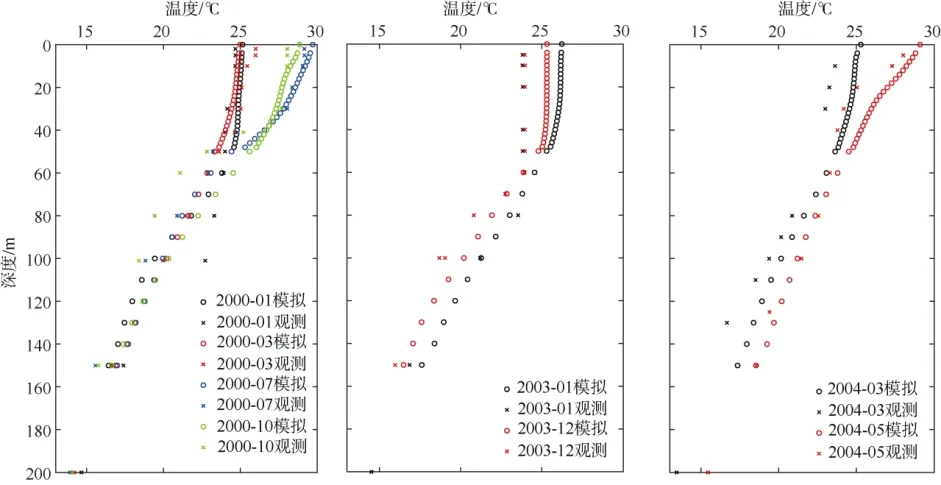
图2 海温模拟观测数据对比Fig. 2 Comparison of simulated and observed ocean temperature

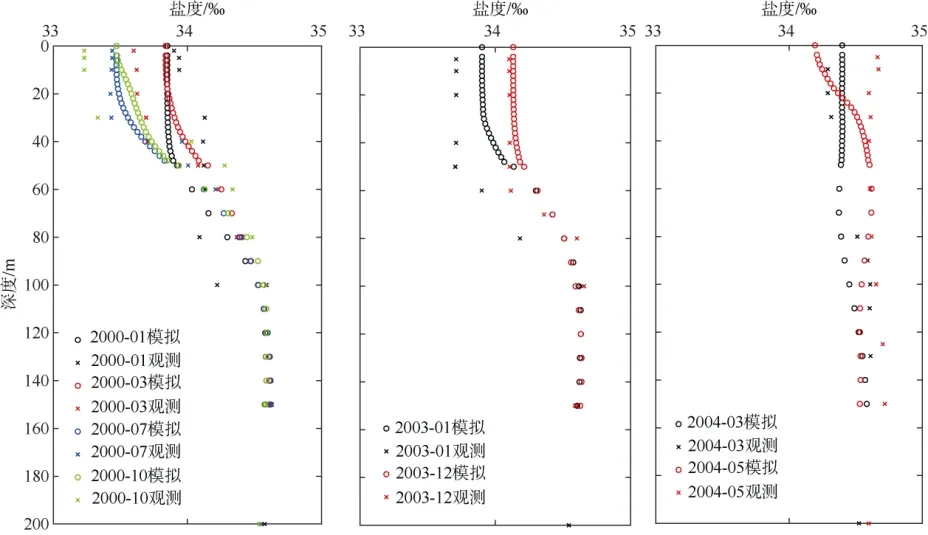
图3 盐度模拟观测数据对比Fig. 3 Comparison of simulated and observed ocean salinity

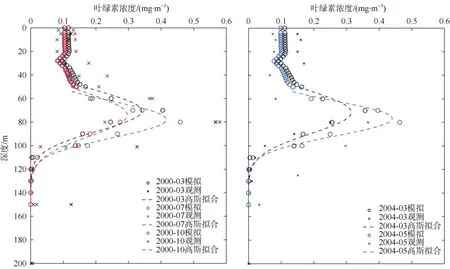
图4 叶绿素浓度模拟观测数据对比Fig. 4 Comparison of simulated and observed chlorophyll concentrations

2.2 SCMs 特征因子年际变化的统计分析

2.2.1 创新趋势分析

对1994—2019 年SCMs 特征因子数据进行创新趋势分析(ITA), 结果如图5。

由图5 可知, 1994—2019 年期间SCMs 的深度和厚度均呈上升趋势, 而强度的散点在y=x直线上下分布为6∶7, 呈较弱的减小趋势; 值得注意的是图中厚度的低值区表现出十分明显的上升趋势(高低区域以横坐标平均线为界, 以垂直虚线表示)。特征因子的总趋势与趋势斜率(强度斜率为-9.5×10-5、深度斜率为3.5×10-3、厚度斜率为1.8×10-3)相吻合。SCMs 强度、深度和厚度的ITA 指数分别为0.03、0.05 和0.07, 故在1994—2019 年SCMs 厚度变化幅度最大, 深度次之, 强度最小。

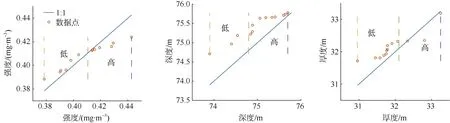
图5 SCMs 特征因子趋势的创新趋势分析Fig. 5 Trend of SCM characteristics by innovative trend analysis

2.2.2 经验模态分解分析

据国家旅游部门统计，2016年我国出境游人数达到1.22亿人次，旅游消费1098亿美元，出境游客人次连续13年以两位数的速度增长，这两项指标连续四年位居全球第一，对全球旅游收入的贡献年均超过13%。与之相伴，中国留学大军也遍布五大洲，2015年总人数首次突破50万，2016达到54.45万人。中国也因此摘得世界第一大留学生输出国的桂冠。

对1994—2019 年SCMs 特征因子数据进行经验模态分解分析, 结果如图6—8。

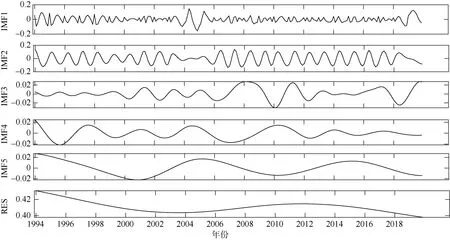
图6 SCMs 强度变化的经验模态分解Fig. 6 Variation of SCM intensity by empirical mode decomposition

由式5 计算可得, 强度IMF 分量的时间尺度分别为2、5、10、18、44 个月。图6 中IMF3 近似体现了强度年际变化过程: 在1994—2006 年趋势变化较为平缓, 2006—2011 年趋势变化较大,2011—2018 年趋势变化再次减缓。IMF5 近似体现了强度以9 年为周期的年代际变化过程。由RES部分可知, SCMs 强度在1994—2004 年有一定幅度的下降, 在 2004—2012 年趋势逐渐上升, 在2012—2019 年趋势再次下降。

由式5 计算可得, SCMs 深度的4 个IMF 分量时间尺度分别为4、11、16、48 个月。图7 中IMF2近似体现了深度年际变化过程: 在1994—2004 和2009—2015 年呈波动变化, 在2004—2009 和2015—2019 年趋势较为平缓。IMF4 近似体现了深度年代际变化过程: 在1994—2005 年不断变深, 在2005—2019 年呈现周期波动。由RES 部分可知: SCMs深度先变深(1994—2011 年), 后变浅(2011—2019年)。

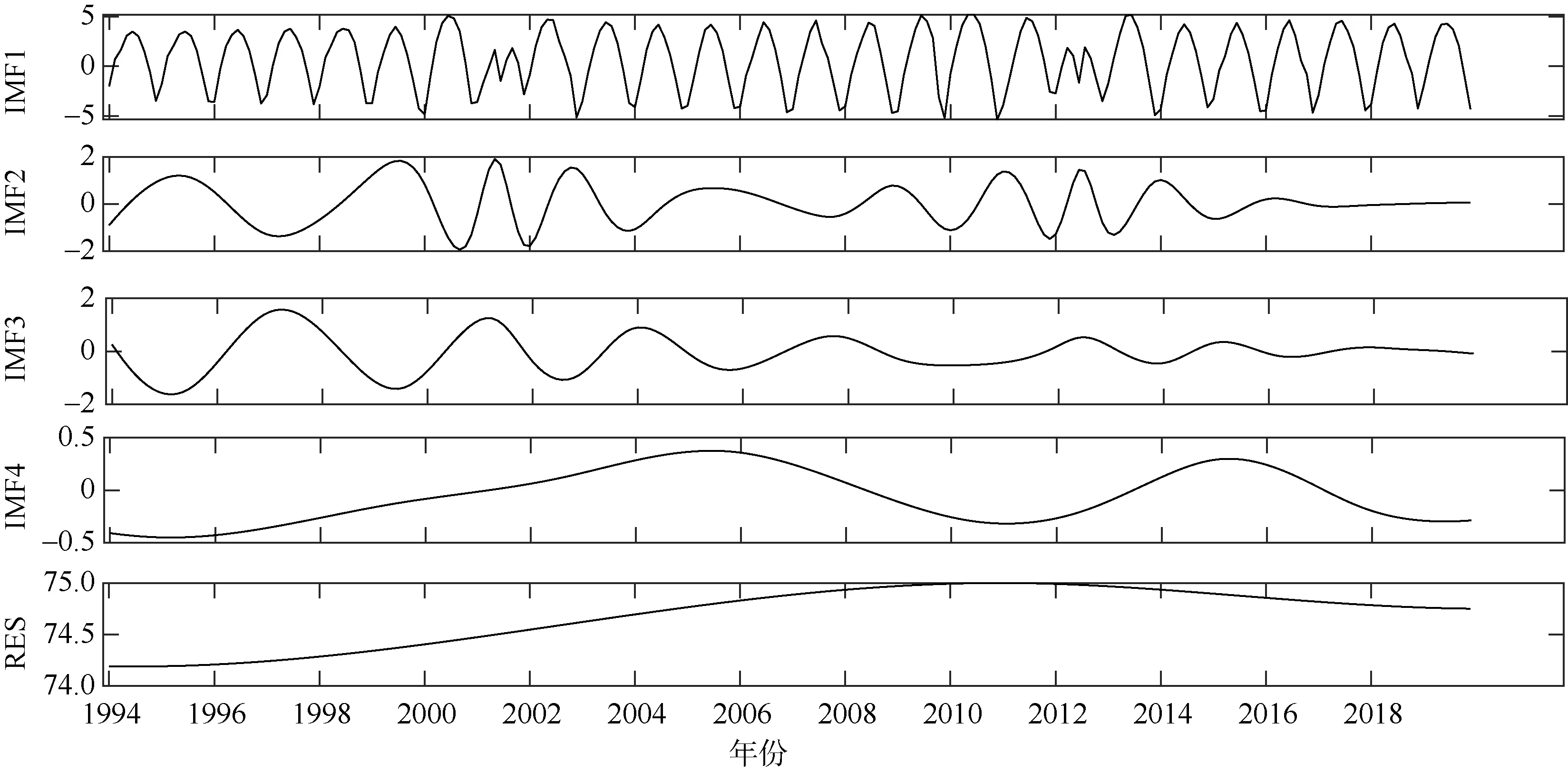
图7 SCMs 深度变化的经验模态分解Fig. 7 Variation of SCM depth by empirical mode decomposition

由式5 计算可得, 厚度IMF 分量的时间尺度分别约为2、4、10、25、43、115 个月。图8 中IMF3 近似表现了厚度的年际变化过程: 1994—2009、2011—2019 年呈现较稳定的周期波动, 但在2009—2011 年维持在较低水平。IMF5 近似表现了厚度年代际变化过程: 1994—2002 年不断变大, 2002—2008 年逐渐变小, 2008—2019 年维持平稳。由RES 部分可知, 1994—2019 年SCMs 厚度呈增大趋势。

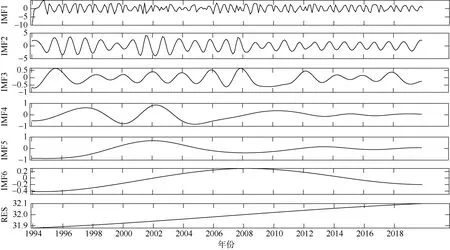
图8 SCMs 厚度变化的经验模态分解Fig. 8 Variation of SCM thickness by empirical mode decomposition

2.2.3 M-K 突变检验分析

对 1994—2019 年 SCMs 特征因子数据进行Mann-Kendall 突变检验, 结果如图9。

图9 SCMs 特征因子变化趋势的M-K 法分析Fig. 9 Trend of SCM characteristics by M-K mutation test

由图9 可知, 厚度在1996 年产生突变(突变点位于95%置信区间内), 整体呈上升趋势(UF＞0), 且于1997 年起上升趋势显著(通过显著水平α=0.05 的检验); 强度于1994 年起点处存在交点, 经改变时间尺度(1994— 2003 年)后做M-K 突变检验发现, 该交点不成为突变点, 1994—2019 年SCMs 强度呈下降趋势(UF＜0), 且1999—2004 年明显减小; SCMs 深度变化不存在突变点, 整体呈上升趋势(UF＞0),1994—1997 年上升趋势不明显, 之后呈显著上升趋势。

综合上述结果可以看出, 在 1994—2019 年SCMs 深度、厚度整体均为上升趋势, 而强度下降趋势不明显; SCMs 强度在2006—2011 年有相对较大的减小趋势, 深度在1994—2004 和2009—2015 年变化相对较大, 厚度在2009—2011 年维持在较低水平; 厚度在1996 年产生突变并于1997 年变为显著上升趋势。

2.3 SCMs 特征因子与海温关系

为理解气候变化相关因素对SCMs的影响, 本文讨论海水温度(表面与深层海温)与SCMs 特征因子的关系。年际变化上, 相关分析结果显示, 海表面温度SST 与 SCMs 三个特征因子均不存在相关关系(P＞0.05)。由SST 与SCMs 三个特征因子标准化后的年际变化序列(图10)可见, 在厄尔尼诺影响下, 1998年和2016 年南海北部海盆区SST 显著升高, 但SCMs三个特征因子变化较小。这表明气候变化导致的海表面升温可能对次表层浮游植物的生长影响不大。

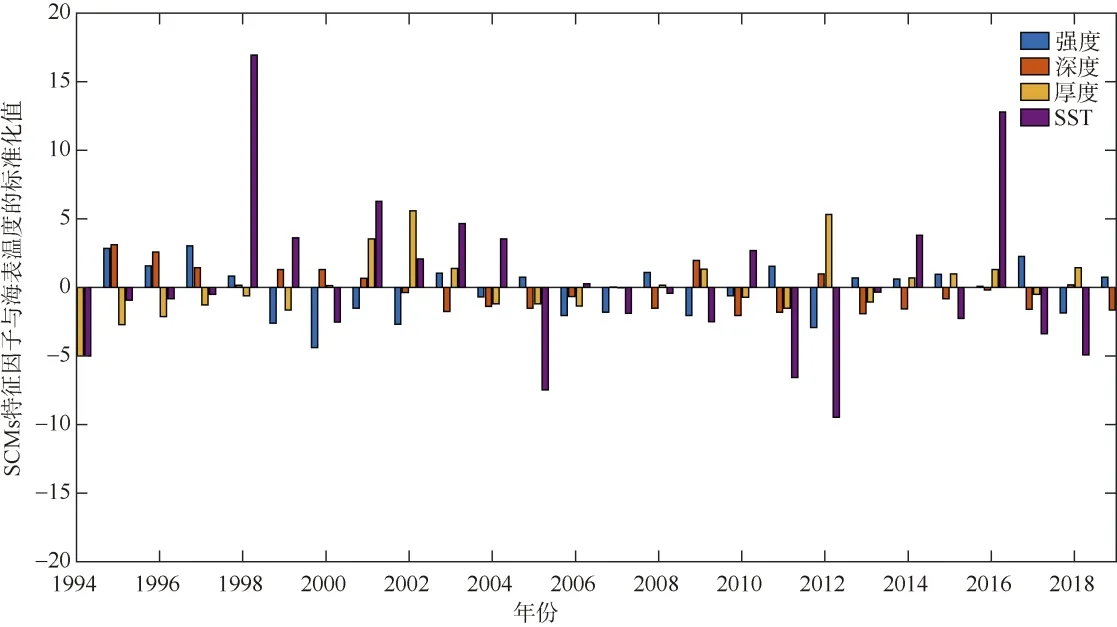
图10 SCMs 特征因子与海表温度标准化值的年际变化Fig. 10 Interannual variation of standardized value of SCM characteristics and SST

月份变化上, SCMs 深度、强度均与海表面温度SST 呈显著的正相关关系(r分别为 0.79、0.49,P＜0.001, 图11), 而SCMs 厚度与SST 不存在相关关系(P＞0.05)。特别是春季和秋季, 随 SST 增加,SCMs 深度显著变深(r分别为0.86、0.81,P＜0.001,表1), SCMs 强度也显著变大(r分别为0.51, 0.69,P＜0.001, 表5)。这可能是由于海表温度上升, 次表层海水密度变小(Midhun shah et al, 2020), 更多表层浮游植物沉降到次表层(Fennel et al, 2003), 导致SCMs 强度变大, 深度变深; 同时由于海表升温使得密度分层得到加强, 上混合层深度变浅, 营养盐垂直向上混合层的输送减少, 表层浮游植物生长受到限制(Lewandowska et al, 2014; Meng et al, 2021),这使得次表层水体中光合有效辐射增强, 因此SCMs 深度和强度随之增加。夏季SCMs 强度和深度与SST 不存在显著相关性或相关性较小, 这可能是由于夏季南海北部海盆区温度较高, 当温度超过一定范围时, 对浮游植物生长的影响较小, 同时由于夏季光辐射较强, 从而导致光抑制作用。而SCMs厚度主要受浮游植物种群结构、生物特性及次表层水体湍混合强度等因素影响(Beckmann et al, 2007;Gong et al, 2015), 与SST 不存在相关性(Midhun shah et al, 2020)。

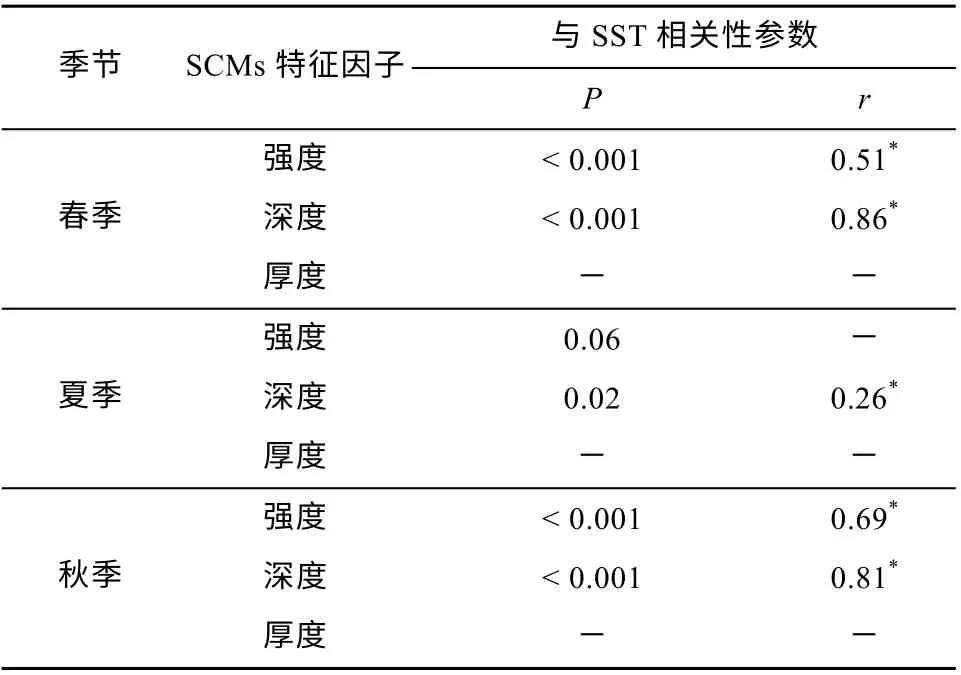
表5 SST 与SCMs 特征因子的相关性Tab. 5 Correlations between SST and SCM characteristics

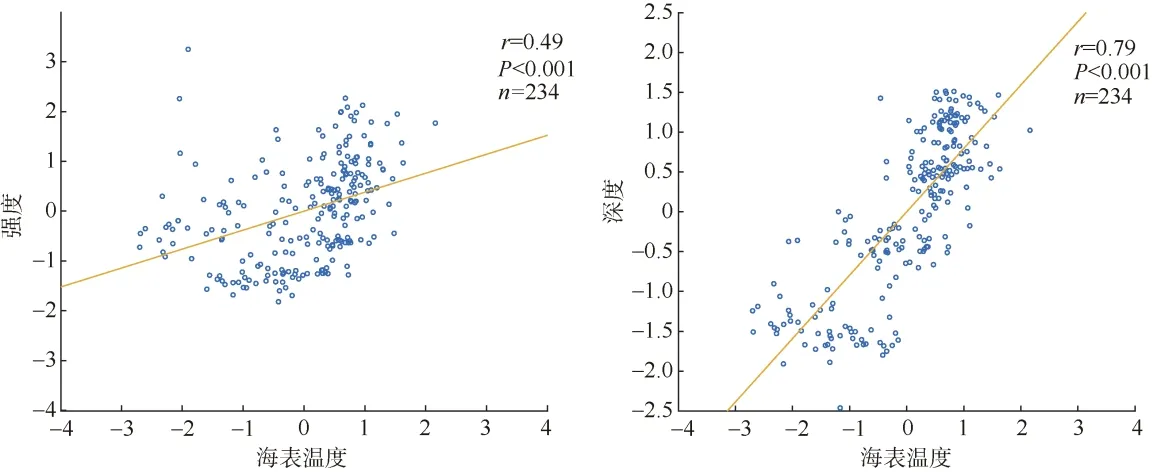
图11 海表面温度与SCMs 强度、深度的线性相关关系Fig. 11 Linear correlations of SST with the intensity and depth of SCMs

为了进一步探讨海水温度与SCMs 特征因子的相关关系, 选取深层海温(SCMs 上边界处、深度处和下边界处海水温度, 各处水深取历年平均值为59、75和91m)与特征因子进行相关性分析, 结果见表6。

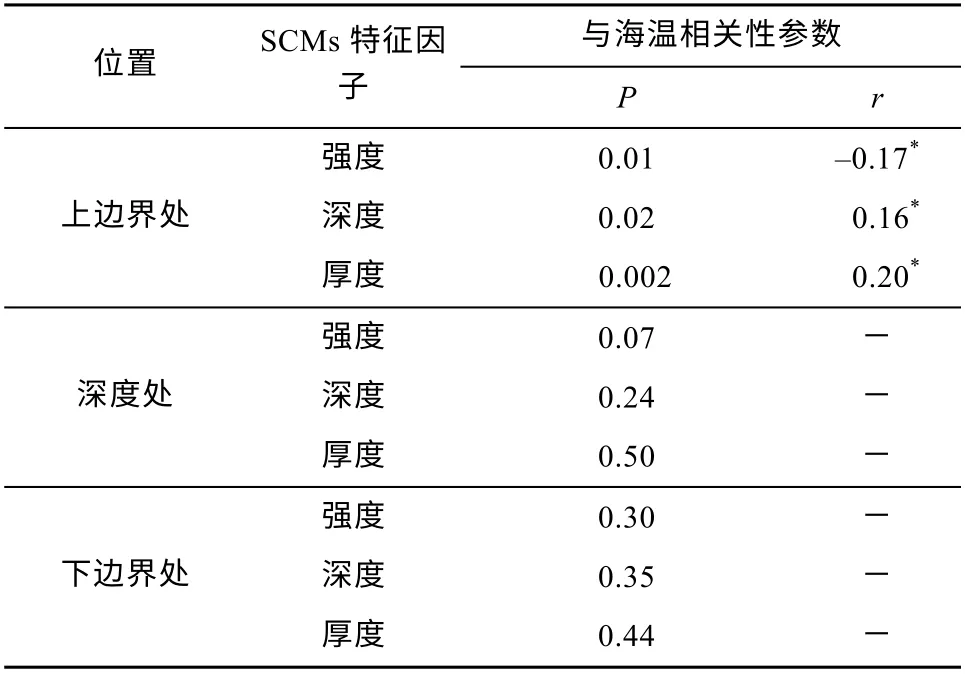
表6 深层海温与SCMs 特征因子的相关性Tab. 6 Correlations between deep-sea temperature and SCM characteristics

由表6 可知, SCMs 特征因子仅与SCMs 上边界处海水温度存在显著相关性(P＜0.05), 但相关系数较小, 强度与其呈负相关, 深度和厚度与其呈正相关, 这表明混合层以深的水温对SCMs 影响不大。南海北部海盆区混合层深度除冬季外均较浅, 约20～40m(Tseng et al, 2005), 而叶绿素峰值多发生60～80m, SCMs 厚度约30m, 其上边界多位于混合层以深15m 处, 上边界处海温增加, 意味着上混合层对营养盐的向上卷挟较多, 次表层浮游植物可在更大范围内快速生长, SCMs 厚度变大, 峰值减小(Beckman et al, 2007)。

2.4 时间序列模型预测

本文首先利用1994－2018 年SCMs 特征因子的月平均值, 根据贝叶斯信息准则(Bayesian information criterion, BIC)得到SCMs 特征因子的最优SARIMA模型, 结果显示: SCMs 强度 SARIMA 模型为

(0,0,1)×(0,1,1)9、深度SARIMA 模型为(0,0,1)×(0,1,1)9、厚度为SARIMA(0,0,0)×(0,1,1)9。

利用所得的SARIMA 模型预测2019 年SCMs特征因子变化趋势, 并采用平均绝对百分比误差(mean absolute percentage error, MAPE)这一指标来评估模型结果(式 10), 可得 SCMs 特征因子的MAPE 分别为5.33%(强度)、0.62%(深度)、2.49%(厚度), 表明SARIMA 模型可用于SCMs 特征因子的预测分析。

式中:T为预测时间,为t时刻的预测值,ty为t时刻的实际值。

为预测2020 年3—11 月SCMs 特征因子的变化情况, 本文利用1994—2019 年SCMs 特征因子的月平均值, 再次根据贝叶斯信息准则确定三个特征因子的最优SARIMA 模型(与1994—2018 年模型相同)。预测结果如图12。如图12 所示, 2020 年3—11月SCMs 强度、深度和厚度的预测值与历史值相差不大, 其极大值与极小值发生的时间基本与历史同期, 表明SARIMA 模型可用于对SCMs 特征因子的预测。

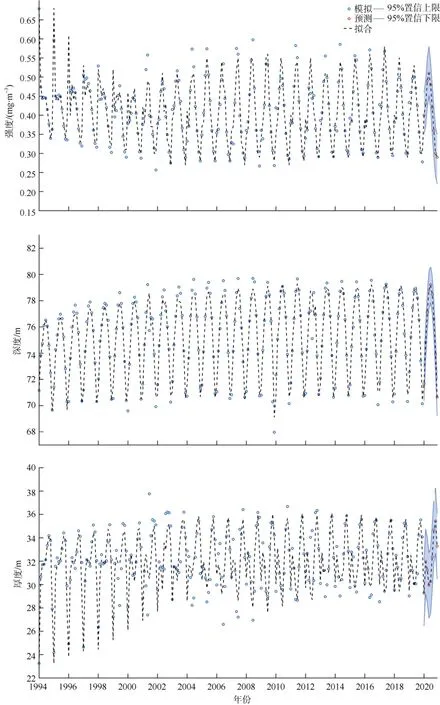
图12 1994－2020 年SCMs 强度、深度与厚度的回归拟合及预测Fig. 12 Regression fitting and prediction of the intensity, depth and thickness of SCMs from 1994 to 2020

3 结论

本文利用MEM-1D 模型模拟了1994—2019 年南海北部海盆区SCMs 现象, 并对模拟结果进行了统计分析, 得到了SCMs 特征因子的年际变化特征,并探讨了SCMs 特征因子变化与海水温度的关系。

在1994—2019 年, 深度、厚度整体均为上升趋势而强度为下降趋势, 厚度在1996 年开始突变并于1997 年变为显著上升趋势。具体表现为, SCMs 强度在1994—2004 年逐渐变小, 2004—2012 年不断增加,而在2012—2019 年强度再次减小; 深度在1994—2011 年不断变深, 在2011—2019 年略微变浅; SCMs厚度在1994—2019 年呈持续上升趋势。年际变化上,海表面温度与SCMs 特征因子间不存在相关性, 表明在南海北部海盆区, 气候变化导致的海表面升温对SCM 层的浮游植物生长影响不大。但在月份变化上, SCMs 强度和深度与海表温度之间均为显著正相关关系, 特别在春季和秋季, 当海表温度上升时SCMs 强度增加、深度变深。深层海温与SCMs 特征因子基本不具有相关性。最后采用SARIMA 模型对2020 年3—11 月的SCMs 特征因子变化做出了预测, 模型评估误差小于10%且预测值与历史同期相近, 表明SARIMA 模型可用于预测SCMs 特征因子变化趋势。