浅谈“灰色关联”在船舶行业内建造生产管理风险的应用

郑尚，伊士超

（1.江苏科技大学计算机学院，江苏镇江 212003；江苏科技大学理学院，江苏镇江 212003）

灰色系统理论是一门具有良好的理论研究与应用价值的学科[1]，灰色系统理论的重要组成部分之一灰色关联分析更是在理论和应用研究中具有很高的地位与作用。灰色关联分析是一种通过灰色关联度的计算来分析和确定系统诸因素间的影响程度或因素对系统主行为的关联程度的方法。灰色关联度的计算方法是灰色关联分析的基础和重要工具。因此，灰色关联度模型的建立与改进更是灰色关联分析的重要讨论课题。

现在灰色关联度理论受到国内外学者的关注和研究，是灰色系统研究领域未来发展和研究的重要分支。实践证明，灰色关联系统在图像识别、天气预报、地质地震、交通运输、医疗诊断、信息控制、人工智能等诸多领域的应用也已初见成效[2-4]。从该学科的发展趋势来看，它具有极其强大的生命力和渗透力，目前在各个领域的应用十分广泛。

1 灰色关联理论

利用灰色关联分析进行综合评价的步骤如下。

建立m个评价方案的n个评价因素：R=（rij）m×n。对评价矩阵进行标准化：

风险灰关联系数矩阵：

2 根据本项目的改进

灰关联分析的最终结果是灰关联度，该指标可以反映所有评价对风险最高评价指标的相互关联程度，但是并不能量化各风险因素在风险评价结果中的综合权重等级。在本项目风险评价应用过程中，在获得风险评价灰关联度后，针对灰关联度最高的前1/3 评价计算评语的平均值，进而分析出综合风险等级。从而可以得到更为直观的应用结果。

3 利用灰色关联理论对建造生产管理风险的评价分析

根据专家评分法利用熵权法获得各风险指标的熵权分配向量W：

指标集和权重分布如图1 所示。

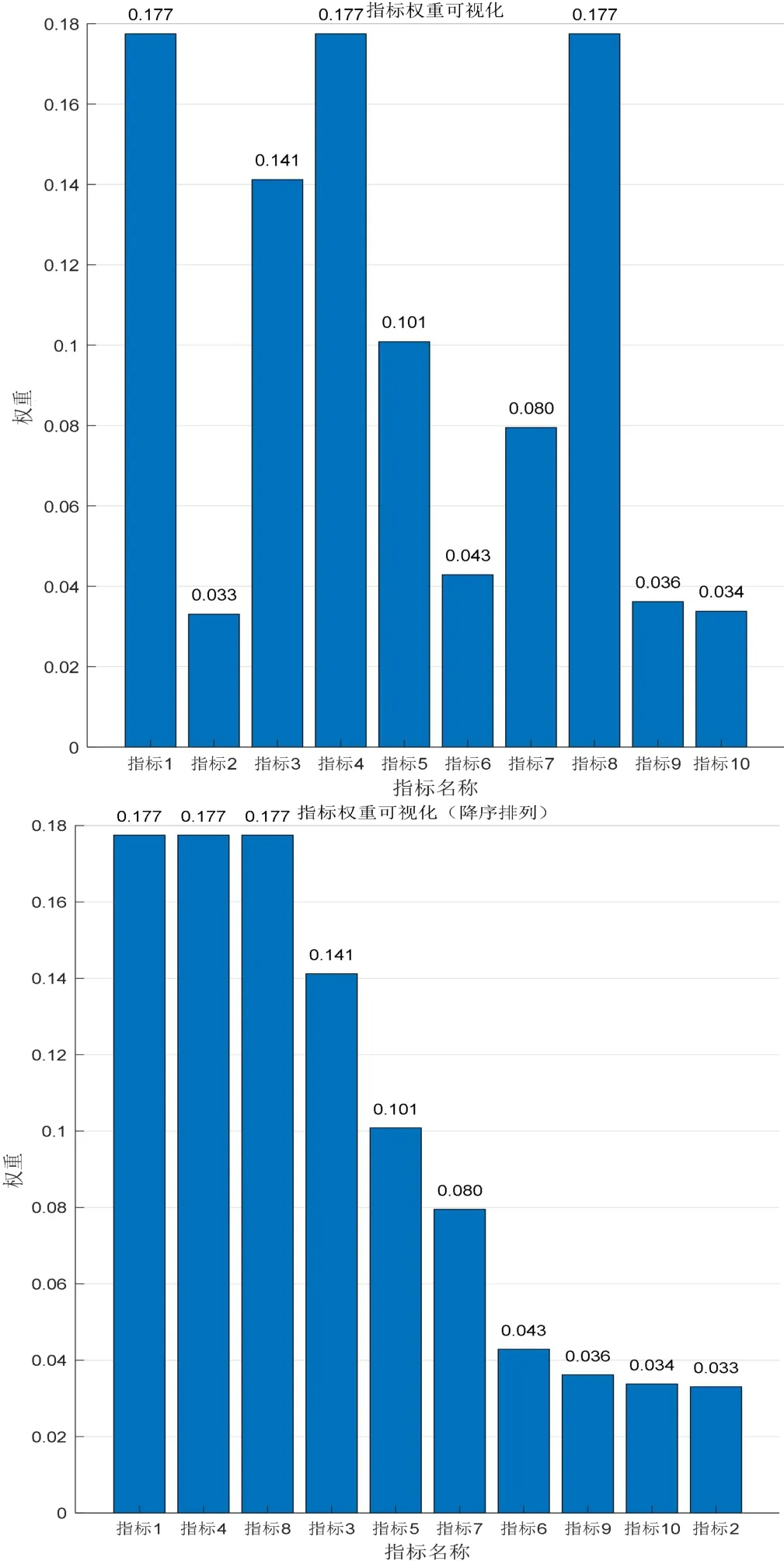
图1 指标集和权重分布

风险的灰关联系数矩阵：

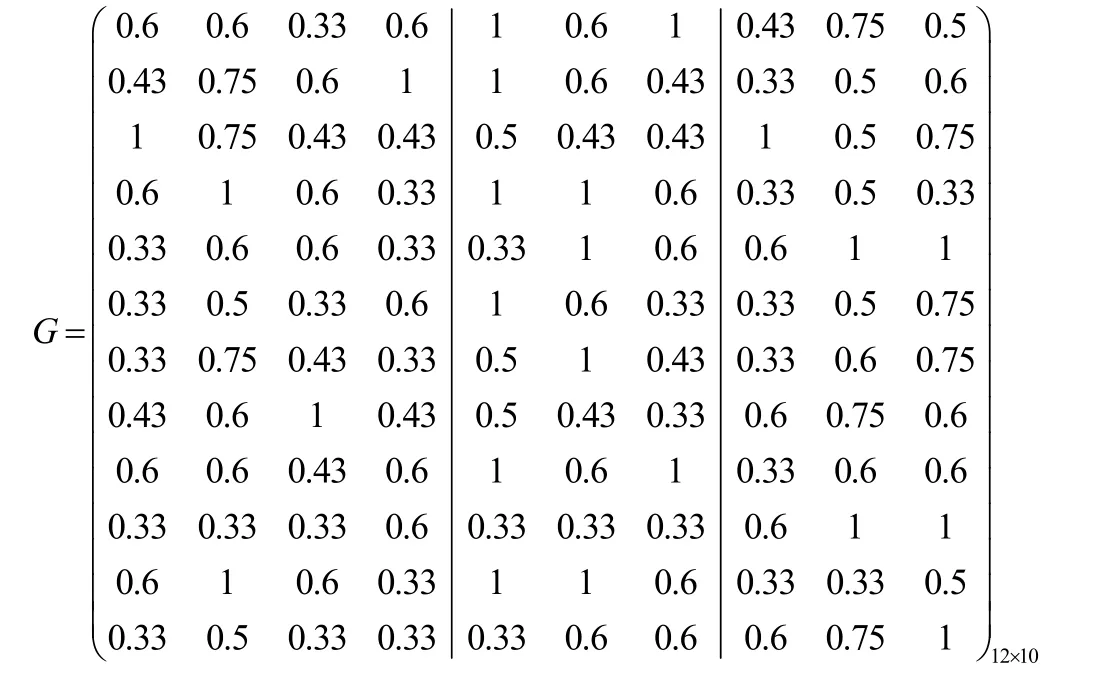
计算灰关联度。灰色评价法对各种方案的灰关联度如表1 所示。样本序号的关联度分析如图2 所示。

表1 灰色评价法对各种方案的灰关联度

图2 样本序号的关联度分析

最高风险关联度前1/3 的4 个评价分别为评价5，10，12，3。对应的评价矩阵为：

各风险因素灰关联度综合评价：73 65 73 73 78 80 78 88 85 93。

在此过程中，获得了灰色评价法对各风险源的评价结论，如表2 所示。

表2 灰色评价法对各风险源的评价

总之，灰色系统理论以模糊数学为理论依据，以风险数据作为数据支撑，利用现行的行业内灰色系统理论设计指标体系，采用模糊矩阵评分法减小人为的主观性，以模糊计分消除两极分值，使量化评价结果更加客观。