宽板弯曲过程中板厚变化规律的数值模拟研究＊

2021-12-04胡一博刘能锋陈如香戴坤添

科技与创新 2021年22期

胡一博，刘能锋，陈如香，戴坤添

（哈尔滨工业大学（深圳）实验与创新实践教育中心，广东深圳 518000）

钣金件有着强度好、稳定性高、加工性能好等特点[1]。弯曲工艺是钣金件最常见的加工方法之一，被广泛应用于汽车行业、航空航天产业、船舶制造业、家电制造业等领域。长期的实践发现，钣金件弯曲过程中板材厚度会发生不同程度的减薄。在冲压行业中，工程人员计算钣金弯曲件板厚的变化往往依靠的是经验表格，缺乏一定的理论支撑。本文通过Deform 有限元分析软件对宽板弯曲工艺进行有限元仿真分析，基于Matlab 软件对有限元数据进行计算分析，绘制板厚变薄系数随着相对弯曲半径而变化的曲线，并对结果进行数值分析求出宽板弯曲中变薄系数和相对弯曲半径关系的数值解。

1 实验前准备

1.1 有限元软件选择

钣金件的弯曲工艺是钣金行业最常见的加工工艺，属于塑性加工工艺的一种。国内外许多CAE 公司为都为塑性成形工艺开发过不同的有限元软件，但是不同软件之间有着明显的差别。有限元分析中最常用的通用有限元软件有Ansys、Abaqus 等，它们虽然适用性广、兼容性高，但是这些软件在前处理的设置（如约束、加载、接触、摩擦条件等）过程中过于烦琐，在对塑性成形过程仿真的使用上有诸多不便。与上述软件相比，针对塑性成形的特点而开发的专业软件在使用过程中更为便捷，此类软件有Deform、Autoform 和Dynaform 等。本文以Deform 软件作为有限元分析软件，进行数值模拟实验。

1.2 宽板弯曲有限元模型简化

宽板弯曲问题在历史上有诸多的研究[2]，普遍认为，宽板在进行弯曲工艺下发生塑性变形的时候，当钣金弯曲件宽度方向上的尺寸远大于其厚度方向的尺寸，板材宽度方向上的变形量可以忽略不计[3]。在这个时候，宽板弯曲问题可以简化为平面应变问题来处理。Defrom 软件中有针对于二维模型开发的Deform-2D 模块，用于分析金属成形及相关材料的各种成形工艺，被广泛应用于平面塑性问题的有限元实验。本文通过应用平面应变模型对宽板弯曲过程中板厚的变化进行研究，用Defrom-2D 软件来模拟平面应变条件下宽板的弯曲过程，追踪变形过程中板厚的变化，对所得数据进行分析，得出结论。

2 宽板弯曲数值模拟实验

2.1 材料选择

钣金弯曲件材料选用10 号冷轧钢板，10 号钢在常温状态下有着良好的塑性和韧性，具有很好的弯曲性能。选择10 号钢作为实验材料有两点考虑：①10 号钢在工程领域应用极为广泛，10 号钢的大部分力学指标在工程上已经被检测出来，可以作为基础数据直接使用[4]；②10 号钢取材方便，为后续的实物实验提供极大的便利。

在Deform 材料库中选择AISI-1010，材料的部分力学参数如表1 所示。

表1 10 号钢的部分力学参数

2.2 有限元实验参数设定

宽板弯曲工艺的二维模型比较简单，由凸模、凹模和钣金件三部分组成。将模型导入Deform-2D 软件中后，将凸模和凹模定义为刚体，二维模型如图1 所示。

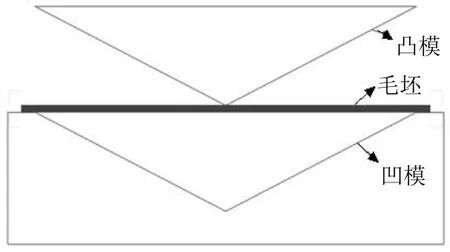
图1 Deform-2D 中的二维模型

为了确保实验的准确度，模拟实验中模具尺寸的选择参考了模具设计手册里面的推荐值。其他实验参数（如摩擦、模具间隙、下压速度等）的选择比较“保守”，目的是确保成形性能良好，尽量减少由于参数选择问题而产生的误差。模具与坯料间摩擦边界条件按常剪切因子摩擦模型施加。具体弯曲工艺参数如表2 所示。

表2 弯曲工艺参数设定

在有限元分析过程中，正确地划分网格会大大提高求解的精度和速率，从而减少数值模拟的时间。本次实验选用四节点网格中的矩形单元来进行网格划分。把宽板划分的四边形网格进行分层，由内层到外层依次为第1 层到第15 层，如图2 所示。

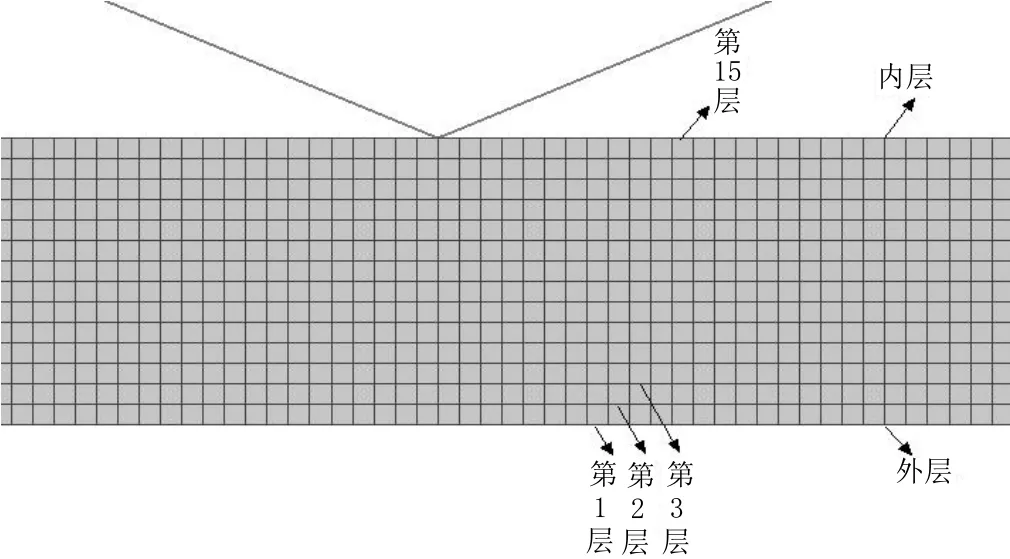
图2 宽板网格划分示意图

本次实验采用10 号钢作为实验用材，部分力学性能上文已经详细阐述。Deform 软件允许用户通过两种方法来建立材料模型，一种是用户自定义材料模型，一种是通过现有的材料库选取材料模型。10 号钢作为常见的实验用材，Deform-2D 的材料库中对其有所收录，参考10 号钢已知的力学性能，对其材料库中10 号钢的性能稍加修改，使其材料模型更贴近实际情况。在本次数值模拟实验中，板材弯曲过程中不存在剧烈的变形情况，因此不考虑微观变形机制，忽略宽板弯曲变形过程中温度的变化[5]，直接讨论宏观参数（摩擦、初始板厚）对流动应力和应变的影响，流动应力-应变模型为[6]：

2.3 其他参数设定

为了使数值模拟结果更加趋近于实际情况，根据现有资料分析整合并对模拟参数进行详细调整，力求达到较为精确的数值模拟结果。具体如下：①板材厚度2 mm。②选用不同的摩擦系数（0.04、0.08、0.12）来对结果进行分析。③选择Newton-Raphson 式的迭代计算方法。④毛坯类型设置为塑性体，且考虑后期的加工硬化现象。模具类型设置为刚体。⑤凸模采用等速给进的方式，为了使模拟结果更加符合实际情况，凸模给进速度设置为1 mm/s。⑥模拟过程中仅使用变形模块，因为过程中保持室温恒温，所以模拟过程中不使用热传导模块。⑦给进的步数根据弯曲程度而定，细化弯曲成形末期的步数，以便更准确地分析结果。⑧储存间隔步数设置为1 步。

3 实验数据分析

3.1 追踪板厚变化

在宽板弯曲过程中，随着弯曲程度的增加，宽板的厚度会产生一些变化。如图3 所示，宽板长度方向的中心，最内层和最外层节点编号分别为N7890 和N7876，分别对应的坐标为（x1，y1）和（x2，y2），由于弯曲变形的对称性，宽板长度中心内外层节点坐标的距离即是板厚，所以板厚为：

图3 板厚计算示意图

在弯曲过程中，只需要追踪每一步下，宽板长度中心上最内层与最外层节点坐标的变化，就能准确地追踪板厚的变化。

3.2 变薄系数与相对弯曲半径的关系

读取每一步下的数据。表3 是初始板厚为2 mm 时（99步之后，步数进行细化，每一步下压量有所减小），不同步数下，相对弯曲半径与板厚和应变中性层位移系数的数据，由于数据总量较多，该表仅列出部分数据。

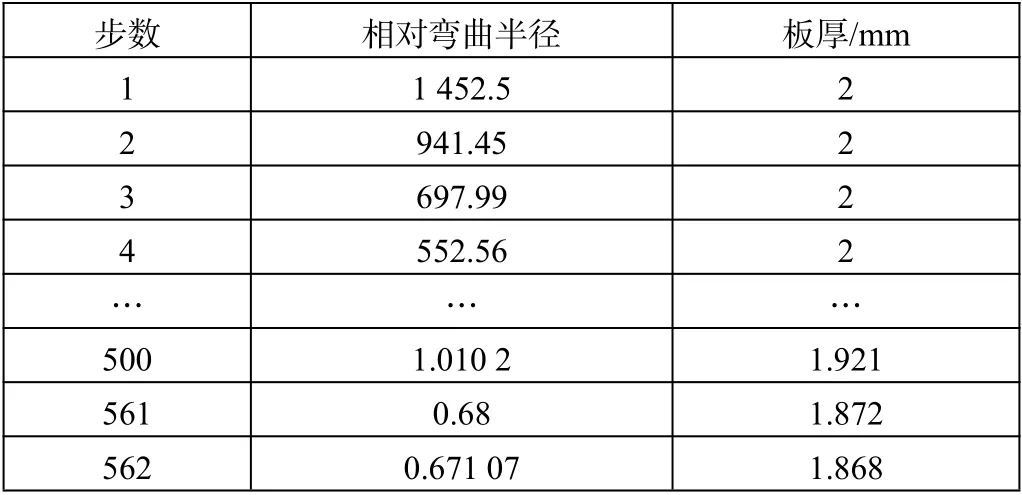
表3 板厚与相对弯曲半径变化数据

根据表3 数据可画出图4 所示曲线，其中横坐标为相对弯曲半径，纵坐标对应的是板厚，由图可以看出，在相对弯曲半径r/t>8 的时候，板厚t基本维持不变。当相对弯曲半径r/t<8 的时候，板厚t开始发生显著的变化。所以，我们把研究重点放在相对弯曲半径r/t<8 的阶段。

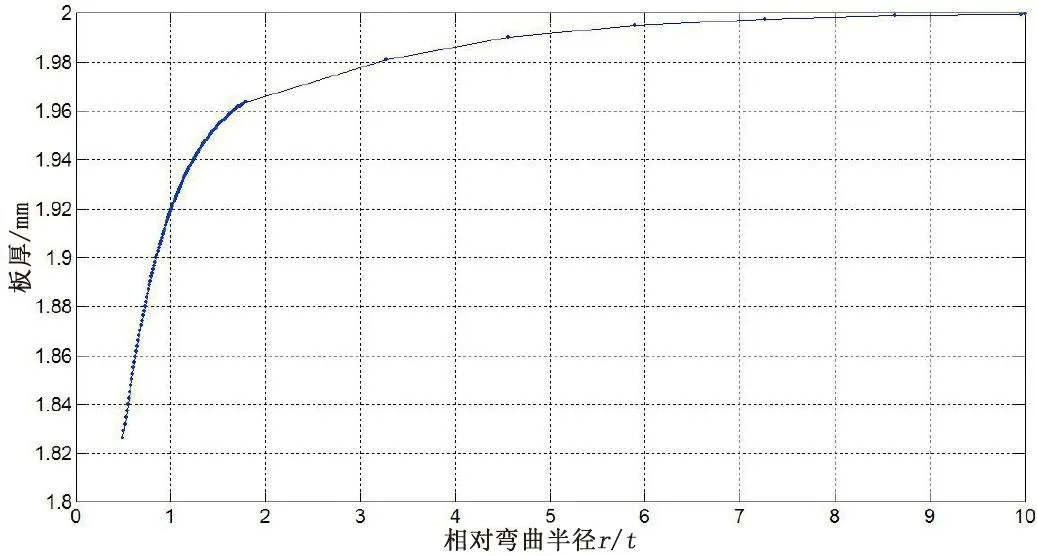
图4 板厚与相对弯曲半径的关系

将板厚随着弯曲进行的变化数据经过处理，可以得出变薄系数和相对弯曲半径的关系，如图5 所示。从图中可以看出，随着弯曲过程的进行，相对弯曲半径r/t逐渐减小，变薄系数η也逐渐减小，即弯曲程度越来越大，宽板的变薄程度也越来越大。从弯曲初期到相对弯曲半径r/t=3 时，变薄系数η接近1，说明此段过程变薄的程度极小。当相对弯曲半径r/t<3 时，随着相对弯曲半径r/t的减小，变薄系数η也急剧减小。即宽板弯曲变形过程中，板厚的减薄阶段主要发生在相对弯曲半径r/t<3 的时候。

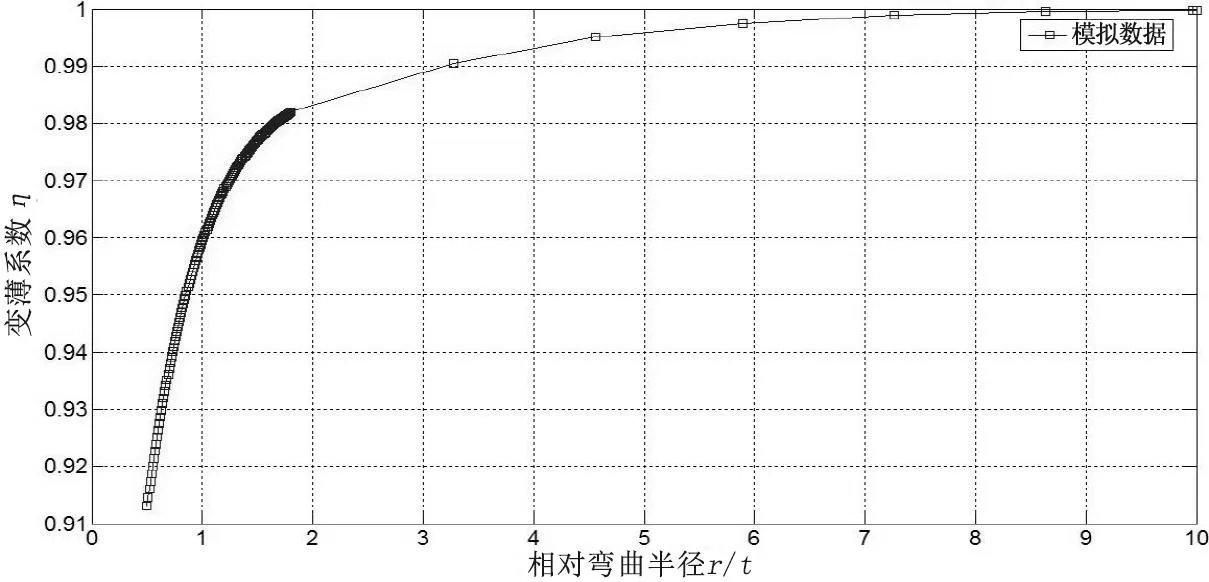
图5 变薄系数与相对弯曲半径的关系

3.3 数据分析求得数值解

变薄系数与相对弯曲半径曲线整体呈现厚度减薄的趋势，弯曲过程前期减薄程度较为微弱，前半段斜率较小，弯曲过程后期减薄程度较为明显，后半段斜率较大。因此，采用指数模型对区域内数据进行拟合：y=aebx+cedx。其中x表示相对弯曲半径r/t，y表示变薄系数η。用Matlab 拟合工具进行拟合处理。拟合结果如下：

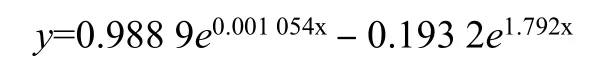
为了探讨摩擦力对变薄系数η的影响，在不改变其他参数的情况下，仅仅改变摩擦系数μ，分别做两组平行实验，来探讨不同的摩擦系数μ对变薄系数的影响。模拟结果如表4 所示。

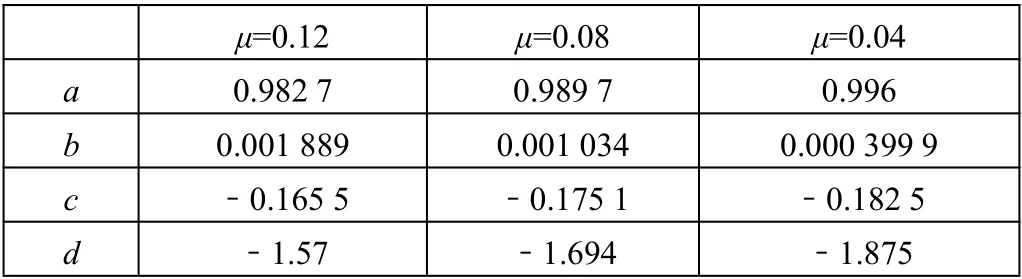
表4 不同摩擦系数μ下变薄系数的拟合结果

图6 是不同摩擦因子下，模拟结果的对比图，从图中可以看出，当弯曲程度较大的时候（相对弯曲半径r/t>9），不同摩擦系数μ下的变薄程度很小，基本相同，变薄系数η接近于1，说明弯曲程度较大时，不同摩擦系数μ下板料的厚度减小程度很小，接近原始板厚t0。随着弯曲过程的进行，弯曲程度越来越大（相对弯曲半径r/t<9），变薄系数η随着相对弯曲半径r/t的减小而减小，但是不同摩擦系数μ下的板料的厚度变化出现了差异，在相对弯曲半径r/t相同的情况下，摩擦系数μ越小，变薄系数η越大，说明随着弯曲程度的增大，板料的厚度开始发生明显的减薄现象，并且摩擦系数μ越小，板厚减薄程度也越小，板厚减薄的速度也越慢，摩擦系数μ越大，板厚减薄程度越大，减薄速度也越快。