变角度铺丝构件内嵌缺陷精确定位算法

钱金源 赵筱彤 王小平 张乐恩

（1 南京航空航天大学机电学院，南京 210016）

（2 南京航空航天大学电子信息工程学院，南京 210016）

文 摘 采用自动纤维铺放技术生产变角度铺丝构件时，在通过平移参考路径方法获得完整铺层过程中剪丝操作将导致构件中产生间隙、重叠形式的内嵌缺陷。将参考路径设计为更具通用性和设计自由度的B样条曲线。针对开边柱面铺丝构件，通过延长参考路径、丝束等距、丝带平移、丝束剪断、缺陷定位步骤，提出了不同剪断策略下的内嵌缺陷精确定位算法，该算法适用于任意覆盖参数。最后开发了相应Matlab程序验证算法的有效性，并可视化铺丝构件中内嵌缺陷的分布情况。结果表明算法可以精确确定不同覆盖参数下内嵌缺陷的位置，可为后续有限元精细模型建立提供理论依据。

0 引言

先进复合材料由于其固有轻质优势，在航空航天、汽车、风电等领域的应用愈发广泛，采用高占比轻质复合材料的飞机可以实现整体减重20%～30%，节能可达18%，获得高成本效益［1-2］。近年来，自动纤维铺放（AFP）技术相较于其他传统铺放技术在复合材料构件生产方面已稳步取得优势地位［3］。自动纤维铺放技术允许层合板内纤维以曲线形式铺放使之具有变刚度特性，称为变刚度或变角度层合板（VSL）［4］，但是在变角度层合板生产中，采用丝束平移方法会导致相邻丝束间产生局部内嵌缺陷，通常表现为间隙（gap）或重叠（overlap），使用AFP 系统中的丝束剪断与重送功能可以减少缺陷面积，但无法避免缺陷生成，最终在单层中产生一系列楔形的缺陷［5-6］。

国内外对于内嵌缺陷已经开展了一定研究，其研究手段包括力学实验与有限元仿真。CROFT［7］通过实验说明铺层内部间隙和重叠缺陷会致使层压板的抗压强度降低5%～27%。李韦清［8］通过实验探讨含缺陷定角度层合板成型方式对拉伸性能的影响。丰亮宽［9］则在定角度试件中通过设置不同的内嵌缺陷角度分析缺陷角度对试件力学性能的影响。FAYAZBAKHSH［10］和NIK［11］借助有限元仿真模拟间隙和重叠的影响，仿真结果说明重叠会一定程度上提高面内刚度与屈曲载荷，而缺陷通常会降低二者。MAROUENE［12］则结合实验与有限元仿真探究间隙与重叠缺陷对变刚度层合板屈曲特性的影响。

对变角度构件开展有限元分析时，通常以不考虑内嵌缺陷的理想铺层简化建模［13-14］。若考虑内嵌缺陷的实际影响，则内嵌缺陷的精确定位算法及几何仿真是后续有限元仿真十分关键且不可获取的前处理过程。BLOM［5］和FAYAZBAKHSH［10］给出了采用等曲率路径作为参考路径的层合板的内嵌缺陷定位算法，该设定下相邻丝束关系便于确定。Mishra［6］则采用均质化方法，显著提高了前处理计算效率。安鲁陵［15］提出了一种丝束裁剪求取算法对丝束重叠程度进行控制，基于此宋桂林［16］给出了规则回转体丝束增减方法及内嵌缺陷面积的近似估算方法。

目前关于内嵌缺陷几何定位算法的研究较为局限，大都以层合板为实验或仿真对象［4-13］，且为便于缺陷定位自动纤维铺放的参考路径大都采用等曲率路径方式铺放［5-6，10-12］，此外，仅针对覆盖参数取为0%或100%［6］两种特殊情况［5，10，12］给出定位方法。本文将层合板构件拓宽至变角度开边柱面铺丝构件，将铺放的参考路径设为更具通用性与设计自由度的B样条曲线，并给出内嵌缺陷在任意覆盖参数下的精确定位算法，最终开发Matlab 程序验证算法并可视化内嵌缺陷的真实分布情况。

1 开边柱面铺丝构件参考路径

开边柱面铺丝构件作为直纹面的一种特例，其参数形式可表达为式（1），如图1所示。

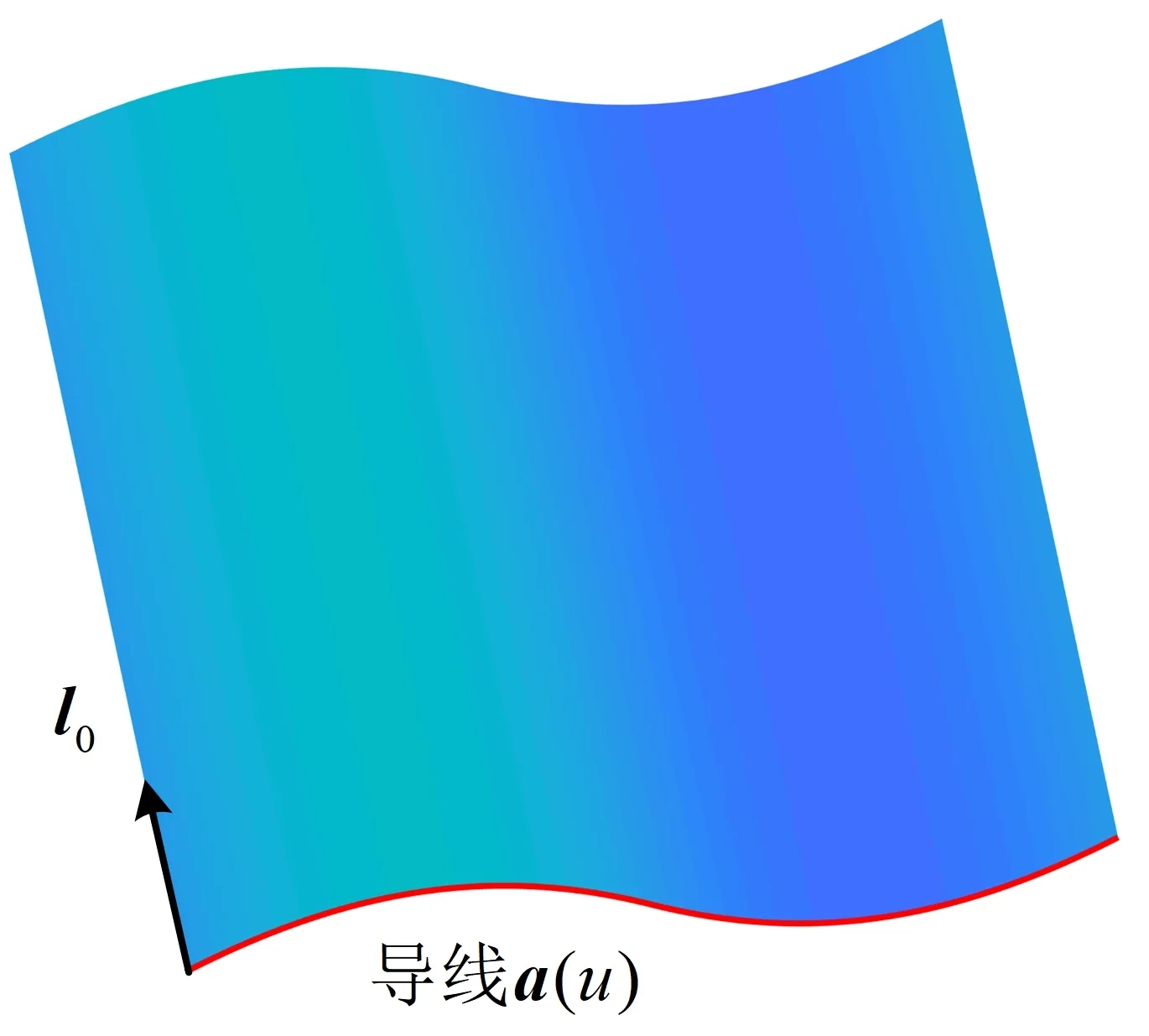
图1 开边柱面构件Fig.1 Open-contoured cylinder component

式中，a（u）为导线，l0为直母线单位向量。

开边柱面可以与平面之间建立保长对应和保角对应，设平面为P（u͂，v͂）且构成正交坐标网，则柱面S（u，v）展为该平面的参数变换关系由式（2）给出，其逆过程由式（3）给出。

式中，b（u）为按变换b（u）=a（u）+λ（u）·l0得到的导线，且满足b′（u）·l0=0，|b′（u）|≠0。

在铺丝构件上铺放纤维丝束时，首先需设计参考路径，然后将参考路径偏移给定的距离，重复该步骤以铺满整个单层。由于开边柱面与平面间具有保长变换关系，可以先在平面内设计参考路径，再通过式（3）变换至对应柱面上。为获得纤维角度连续变化的铺层，参考路径采用二次B 样条曲线进行设计，其优点在于路径的首末端点就是控制多边形的首末顶点且路径与控制多边形在端点处相切。若给定初始角度θ1、终止角度θ2、形状参数μ、路径投影长度pro及控制顶点中任意一点，则控制多边形其余顶点可按式（4）求解。可得式（5）的B 样条曲线，如图2所示。

图2 二次B样条曲线Fig.2 Quadratic B-spline curve

式中,V0、V1、V2为控制顶点；lr为平面内参考路径纤维角度的参考方向。

求得控制顶点后，可以根据德布尔算法［17］求得参考路径任意点的切矢p′（t），纤维铺放角度按式（6）求解，式（6）与θ1、θ2、μ隐式相关，形状参数μ过大或过小都将使路径表现得更直，如图3所示。

图3 形状参数μ对参考路径的影响Fig.3 Influence of shape parameter μ on reference path

由于B 样条曲线具有局部性质，通过增加新的控制顶点延长参考路径并不会影响已经设计好的路径，设计更为自由且各部分彼此独立，若参考路径包含m个部分，则控制顶点可按式（7）计算，重复顶点不重复计入，共计2m+1 个，新的节点矢量按弦长参数化方法［17］确定，参考路径如式（8）所示。为了获得路径的G1连续性，新的控制多边形需要与原控制多边形在公共点彼此相切。因此，基于二次B 样条曲线参考路径生成的单层铺层可表示为＜θ1，1（μ1）θ1，2（μ2）θ2，2···（μn）θn，2＞，若参考路径只含有两部分且两部分中心对称，则可简化表示为＜θ1，2（μ2）θ2，2＞。通过平移法可得到不考虑内嵌缺陷的理想铺层，变换至开边柱面铺丝构件的对称理想铺层如图4所示。

图4 ±＜10（0.6）50）＞理想铺层Fig.4 ±＜10（0.6）50）＞Ideal ply-up

式中，N为按弦长参数化方法得到的节点矢量。

2 内嵌缺陷定位算法

在纤维自动铺放过程中，每次在铺丝构件上铺放的纤维复合材料包含若干根单根丝束（tow），这些单根丝束组成一丝带（course），如图5所示。

图5 丝带平移Fig.5 Shifting of courses

丝带内丝束数（tow number）及丝束宽度（tow width）为生产参数，二者乘积为丝带宽度（course width），若不考虑丝束褶皱，则丝带宽度在铺放过程中被认为是定值。从图5 中发现丝束平移法实际为丝带的整体平移而不仅是参考路径的平移，因而存在未能覆盖的区域，同时相邻丝带之间出现较大面积的重叠，借助自动铺丝技术中的剪丝与重送功能可使缺陷的最大宽度减小为单根丝束的宽度，这将最终导致单层中内嵌缺陷的产生。

内嵌缺陷的精确定位算法流程图如图6所示，对于每个单层，主要思路是首先延长参考路径使丝带内所有丝束均能够抵达构件边界，其次通过等距方法求取丝带内所有丝束的轨迹，然后对丝带进行平移以铺满整个铺丝构件，之后采取不同策略对丝束进行剪断并计算相应剪断点，最终实现内嵌缺陷的精确定位。

图6 内嵌缺陷定位算法流程图Fig.6 Flow chart of location algorithm of embedded defects

2.1 参考路径延长

所设计的B 样条参考路径具有局部性质，其延长部分仍可按式（7）计算而不影响延长前的路径，参考路径需要延长直至相应丝带最外侧丝束抵达构件边界，需满足条件（9），该条件下延长部分的终止角度小于初始角度，因而不会超过先前路径的纤维角度范围。延长后参考路径的节点矢量仍按弦长参数化确定。

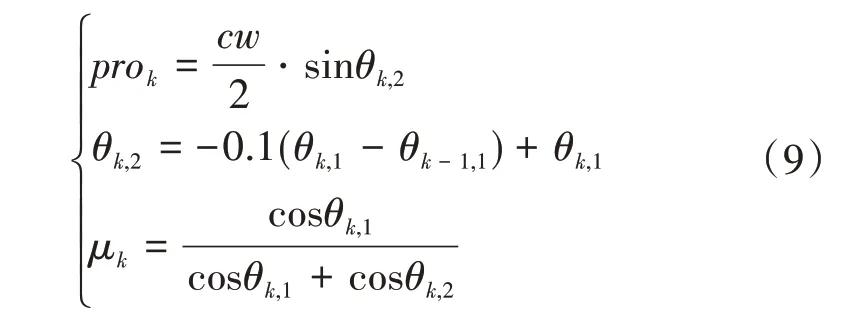
式中，cw为丝带宽度，等于单根丝束宽度与丝带内丝束数的乘积。

2.2 丝束等距及丝带平移

由于相邻丝束之间的距离为单根丝束宽度，铺放过程中是保持不变的，因而将问题转化为求解平面曲线的等距偏移曲线问题，对于任意的参数t0需满足式（10）。

式中，Ok（t）为偏移后曲线，p（t）为参考路径，k∈[-tn∕2，tn∕2]且为整数，tn为丝带内丝束数，tw为丝束宽度，N（t0）为参考路径的单位法向量。

为了高效获得丝带内所有丝束边界的B 样条参数表达形式，不能简单将按式（10）求得的一系列点拟合为B 样条曲线。由于参考路径的曲率半径远小于偏移距离，因而偏移后曲线不会产生尖点或环，采用偏移控制多边形同时不断插入节点的方法求解偏移曲线。偏移得到的样条曲线Ak（t）与真实偏移Ok（t）之间的误差可按式（11）判定，采样点的个数按文献［18］设置。参考路径偏移后的结果已展示在图5中。

为使丝束铺满整个铺丝构件且产生的重叠尽可能少，丝带平移的距离d应为丝带在平移方向上的宽度的最小值，如式（12）所示。平移得到丝带集合记为C。

式中，φmin为沿参考路径纤维铺放角的最小值。

2.3 丝束剪断策略

丝带平移之后，相邻丝带间会出现重叠现象，如图5所示，使用剪丝与重送功能时丝束将沿纤维角度的法向方向被剪断，剪断位置与采用的覆盖参数（coverage parameter）有关。图7 展示了不同覆盖参数对剪断位置的影响，其中边界曲线为相邻丝带的边界线，覆盖参数选为0%情况下，当丝束某一边界抵达边界曲线时立即剪断丝束，这将产生没有纤维的间隙区域，称为完全间隙情况；若覆盖参数选为100%，则当丝束两边界均抵达边界曲线时才剪断丝束，因而产生重叠区域，称为完全重叠情况。覆盖参数选为其他中间值时，间隙与重叠将同时存在。丝束剪断过后而在铺层内最终形成的楔形缺陷即称为内嵌缺陷。

图7 不同覆盖参数下丝束剪断Fig.7 Tow drop under different coverage parameter

为描述方便，将i、j分别定义为丝带编号和丝束编号，将平移法得到丝带集合C中沿平移反方向第i个丝带记为Ci，该丝带内沿平移反方向第j个丝束边界曲线记为tbi，j，由丝束边界曲线tbi，j及tbi，j+1定义的丝束记为ti，j，i、j的含义以下适用。

为求得剪断点，先计算丝带内丝束与边界曲线之间的交点，边界曲线记为Bi（t），依次取为Ci中的tbi，tn+1，tbi+1，j与边界曲线的第k个交点记为ipi+1，j，k，构成集合Ipi+1，j。一条边界曲线与相邻丝带的交点结果如图8所示。边界曲线与丝束边界曲线的交点一般有两个交点。求得的交点结果为空间坐标值，还需通过点反演的方式变换为所属丝束边界曲线的参数值，参数坐标命名为相应空间坐标名称追加p。

图8 边界曲线与丝带交点Fig.8 Intersection points of boundary curves and course

下面给出完全间隙情况与完全重叠情况下的丝束剪断策略（完全间隙策略及完全重叠策略）下的剪断点求解方法，丝束ti，j的剪断点集合记为Tpi，j，相应第k个剪断点记为tpi，j，k，k至多为2。完全间隙策略下，当丝束任一边界抵达边界曲线Bi（t）时立刻剪断丝束，剪断点集合Tpi，j就是Ipi，j。完全重叠策略下，丝束的全部边界都抵达边界曲线Bi（t）时才进行剪断，剪断点集合Tpi，j为Ipi，j+1。

当覆盖参数取为其他值时，将会出现重叠与间隙同时存在的情况，剪断点将不再是边界曲线与丝带的交点，记第i个丝带的参考路径为Ri（u），相应的单位法矢向量为Ni（u），则当覆盖参数cp取为β时，求解式（13）即可求得剪断点，剪断点通常有两个解，分布在丝带的两侧，若丝束ti+1，j两丝束边界曲线与边界曲线Bi（t）均无交点，则方程（13）无解，当β取为0或1时，方程退化为计算丝带内丝束与边界曲线之间的交点问题。一种剪断情况如图9所示。

图9 任意覆盖参数剪断点求解Fig.9 Points for arbitrary cp solution of tow drop

将剪断点tpi+1，j，k变换为所属丝束边界曲线的参数值记为tppi+1，j，k，属于集合Tppi+1，j。

除了以相邻丝带的底端丝束边界曲线tbi，tn+1作为边界，还需要考虑铺丝构件的外形边界对丝束的限制，只需将外形边界作为新的边界曲线计算与丝带的交点，并采用完全重叠策略求得剪断点。至此我们可以获得任意覆盖参数下的丝束剪断位置。

2.4 内嵌缺陷精确定位

丝束剪断后单层铺层内将产生相应的内嵌缺陷。所谓内嵌缺陷定位是指若给定铺丝构件上任意一点p，判断其位于内嵌缺陷区域还是正常纤维区域。首先需要确定丝束剪断之前给定点p所属丝束的编号i与j，点p向参考路径Ri（u）正交投影，投影点记为q=Ri（pp），pp为其参数值，然后求解方程（14）。由于剪断操作前相邻丝带间存在重叠，因而位于重叠区内的点p，将有两个解i1、i2，取二者中较大的值。

式中，r为丝带平移方向向量，ceil为向上取整函数。

获得点p所在丝束ti，j的编号后，为便于描述，将完全间隙情况下的剪断点集合另命名为GTpi，j=｛gtpi，j，k｝，将完全重叠情况下的剪断点集合记为OTpi，j=｛otpi，j，k｝，相应的参数集合分别记为GTppi，j=｛gtppi，j，k｝、OTppi，j=｛otppi，j，k｝。对位于丝束ti，j内的点p，其对应参数坐标pp通过求解式（15）获得，采用完全间隙策略时若p位于间隙处，则须满足式（16），采用完全重叠策略时若p位于重叠处，其到编号i-1 丝带的参考路径法向距离小于丝带宽的一半，则须满足式（17），而当覆盖参数取为β时，记对应的剪断点为itpi，j，k，相应参数坐标为itppi，j，k，判断是否位于间隙时须满足式（18），判断是否位于重叠时须满足式（19），如图10所示，当β=0时，式（18）退化为式（16），当β=1时，式（19）退化为式（17）。通过上述算法，给定构件上一点，对于任意覆盖参数取为β均可判断其是否位于内嵌缺陷区域，且能够判别具体位于空隙区域抑或是丝束重叠区域。

图10 内嵌缺陷定位Fig.10 Location of embedded defects

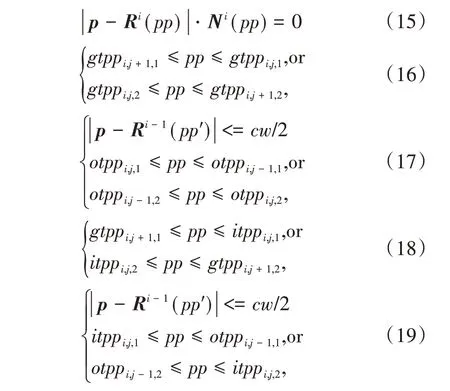
3 实例验证

为验证本文所述内嵌缺陷精确定位算法的正确性及有效性，使用MatlabR2018 软件开展数值仿真实验并可视化铺丝构件中内嵌缺陷的分布情况。铺丝构件为B 样条基表示的开边柱面，参考路径采用本文提出的二次B 样条曲线并已相应延长。以下实例的丝束数量及丝束宽度均分别取为8、6 mm。

3.1 单层铺层实例

铺层采用＜10（0.6）50（0.48）46）＞铺放方式，当覆盖参数选为0%、50%、100%时，即对应完全间隙情况、中间情况、完全重叠情况，铺丝构件内嵌缺陷分布分别如图11～图13所示，图中，蓝色区域表示间隙缺陷，红色区域代表重叠缺陷。

图11 覆盖参数0%内嵌缺陷分布Fig.11 Distribution of embedded defects for cp 0%

图13 中间隙的分布情况具有图11 的分布特征，图13 中重叠的分布情况也继承图12 的分布规律，这与算法描述的规律是一致的，覆盖参数选为0%或100%是两种特例。

图12 覆盖参数100%内嵌缺陷分布Fig.12 Distribution of embedded defects for cp 100%

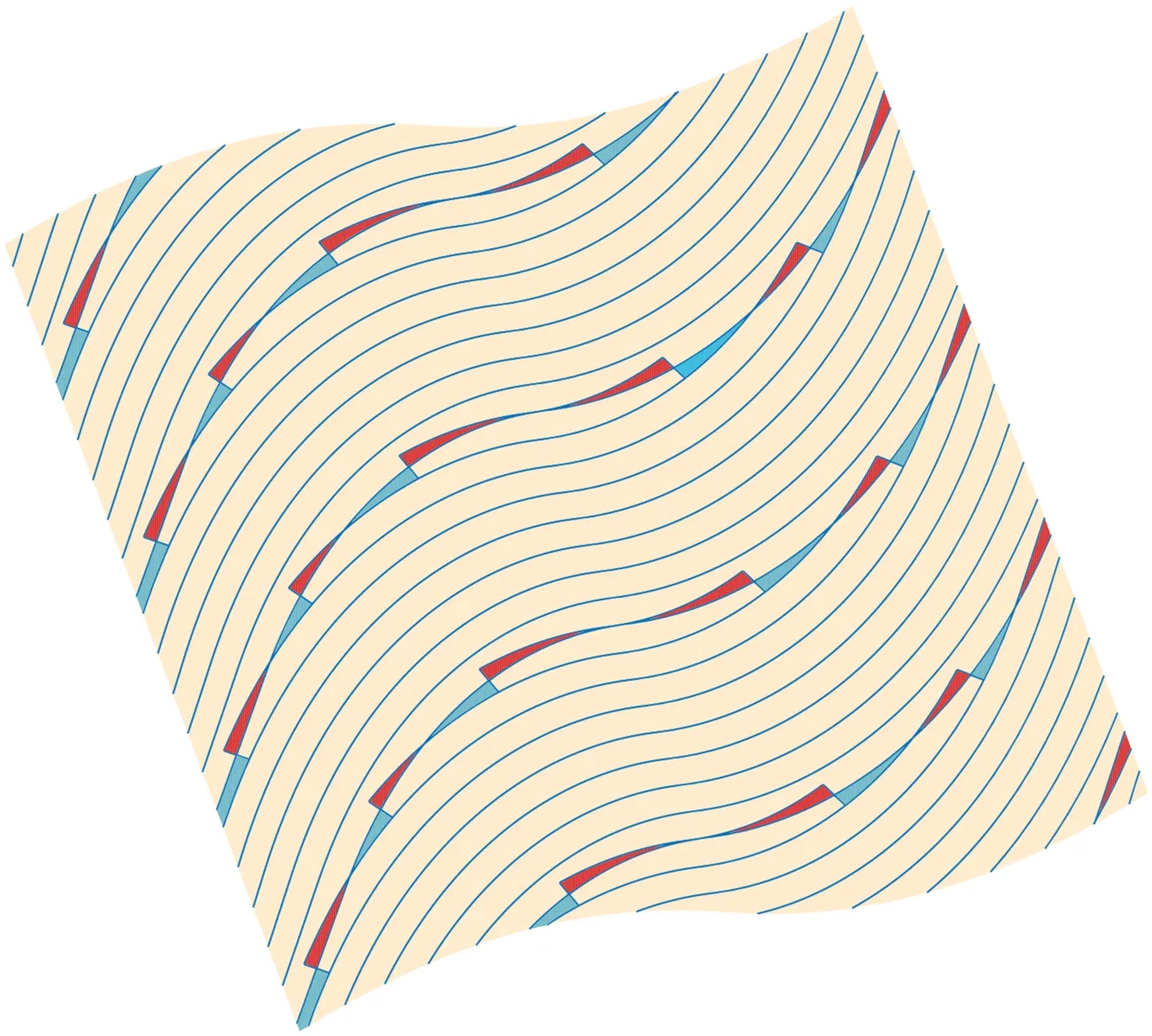
图13 覆盖参数50%内嵌缺陷分布Fig.13 Distribution of embedded defects for cp 50%

3.2 多层铺层实例

铺层采用［±＜10（0.6）50（0.48）46）＞∕±＜20（0.6）40（0.49）38）＞］s铺放方式，这里将铺丝构件进行网格划分，离散为大量壳单元体，依据本文内嵌缺陷精确定位算法判断各单元体是否位于内嵌缺陷区域。覆盖参数选为0%，铺丝构件内间隙分布情况如图14所示。其中图例百分比表示沿铺层厚度方向单元体内间隙量的平均占比，0%代表完全没有间隙的区域，而100%代表沿铺层厚度均为间隙的区域。本文算法可以真实再现多层铺层铺丝构件中的内嵌缺陷分布，因而可为后续有限元精细模型建立提供理论基础及建模依据。

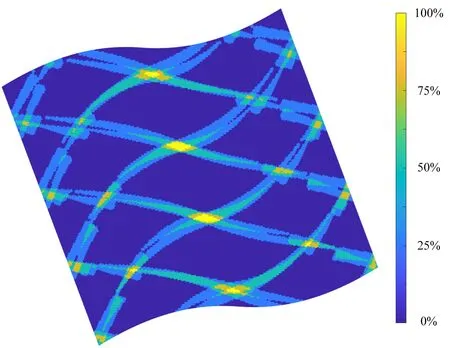
图14 多层铺层间隙缺陷分布Fig.14 Distribution of gaps in multi ply-ups

4 结论

采用平移丝束法生产变角度铺丝构件时，间隙和∕或重叠形式的局部内嵌缺陷会不可避免的产生。基于本文提出的更具设计自由度的B 样条参考路径，为了确定开边柱面铺丝构件铺层中内嵌缺陷的位置及分布特征，提出了一种内嵌缺陷精确定位算法，并给出了具体详细的算法步骤，除了适用于完全间隙策略及完全重叠策略，亦可确定任意覆盖参数下的内嵌缺陷分布，实例仿真表明该算法可以精确定位内嵌缺陷位置，真实再现铺丝构件中的内嵌缺陷分布，并可为后续相应有限元分析中的缺陷建模提供算法依据。