深空极低温服役环境下材料力学∕物理性能低成本快速评价方法研究进展

麻建坐 李卫国 高 鸿 杨梦卿 张续耀

（1 重庆大学航空航天学院，重庆400030）

（2 重庆工业职业技术学院，重庆 401120）

（3 中国空间技术研究院，北京 100094）

0 引言

随着我国空间探测卫星、深空探测飞行器等高端装备的快速发展，对宇航材料的低温服役性能提出了越来越苛刻的要求［1-3］。在低温环境条件下，材料的力学∕物理性能和常温相比有很大差异［4］，了解并评价材料在低温下的力学、物理特性已成为人们关注的重点问题，对航天器结构设计和服役安全性至关重要。

目前我国在低温环境下常用的金属材料有奥氏体不锈钢、铝、铜、钛合金以及镍基合金等［5］。服役温度对金属材料的力学性能影响十分显著，大量学者为了研究金属材料的低温力学性能已开展了相关实验研究工作，并取得了系列进展［4，6-7］。然而极低温力学性能测试需要对被测试样营造极低温环境，目前获取极低温（4.2～77 K）的主要手段是使用液氦作为致冷介质，我国市场上的氦气主要依靠进口［4］，而西方强国将氦气列为战略储备物质限制出口［4］。此外，极低温力学性能测试还依赖于在极低温下可以工作的传感器（如应变、位移、扭角等变形传感器）的发展，目前的实验条件还不能完全满足工程应用的需求［1，7］。与此同时，目前常用的力学性能测试需制备标准试件，属破坏性实验，不能实现实时在线测量。因此，进一步丰富和深入研究材料低温性能表征理论方法，建立材料低温性能理论表征模型，通过易获取的量对材料低温下难以获取的力学性能进行表征和低成本评价非常必要且重要。

半导体材料、磁存储和磁致伸缩材料等被广泛应用于航空航天、微电子、信息存储等高新技术领域［8-10］，在其应用中，常遭受低温环境，而其物理性能受温度影响十分显著，致使以上这些材料体系的研制及在高端装备上的应用依赖于对其低温物理性能理论表征上的突破，开展材料低温物理性能理论表征研究具有重要的意义。

本文总结与评述深空极低温服役环境下材料力学∕物理性能低成本快速评价方法方面的研究工作。囿于篇幅，同时为避免面面俱到，着重介绍极低温环境下材料屈服强度、弹性模量、理想拉伸强度、硬度等力学性能的低成本快速评价方法；极低温下半导体材料的禁带宽度、折射率、拉曼频移以及金属材料磁晶各向异性常数等物理性能的低成本快速评价方法方面近年来本课题组的研究进展。最后对材料力学∕物理性能低成本快速评价方法研究进行展望，并为材料力学∕物理性能低成本快速评价的进一步研究提供建议。

1 材料低温下屈服行为快速评价方法

金属材料在低温下的应用越来越广泛，作为决定材料安全服役的关键指标——屈服强度，对温度非常敏感，特别是当前对复杂热环境下邻近屈服点设计的需求愈发强烈，因此对温度相关性屈服强度的精确获取提出了更迫切的需求，相关研究成为当前高新科技最活跃的领域之一。目前，对低温屈服强度的获取仍主要依赖于实验手段，需制备标准试件，属破坏性实验，难以实现在线测量，也面临着耗时耗力等问题；而现有的温度相关性屈服强度理论模型包含大量拟合参数，致使其使用仍依赖于不同温度下大量实验的开展且不便于工程应用，如何定量表征温度对力学性能的影响是一个亟需解决的难题。因此，建立温度相关性屈服准则并建立相应的理论表征模型，通过易获取的量对材料难以获取的力学性能进行表征和低成本评价，具有重要的理论意义和工程应用价值。

1.1 金属材料温度相关性屈服强度快速评价方法

基于力与热能均可破坏材料化学键的物理事实，李卫国等［11］提出了如下可定量考虑温度对材料力学性能影响的新方法——力-热能量密度等效原理，主要思想是：（1）对一种特定材料，认为其存在一个储能极限，即材料发生破坏时对应一个固定不变的能量最大值，这个最大值可以用应变能表征，也可以用热能表征；（2）从对材料破坏效果讲，材料储存的热能与应变能之间存在一种定量的等效关系。力-热能量密度等效原理为材料高温断裂强度理论表征开辟了新途径，并已在多种材料体系的温度∕尺寸相关性力学∕物理性能等的理论表征上获得应用［8-9，12-19］。为航空航天、核工业、微电子等领域高端装备上关键材料的应用、设计及可靠性评价方面提供了理论基础和技术储备。

基于力-热能量密度等效原理［11］，李卫国等［12，20］提出了一个新的温度相关性屈服准则：“不同温度时，无论在何种应力状态下，当变形体单位体积弹性形变能量与相应温度下与弹性形变能量等效的热能之和达到某一固定不变的定值时，材料进入塑性状态”，由此可得下式：

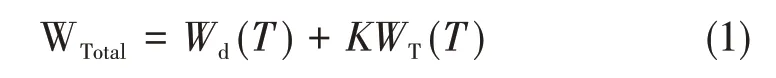
式中，WTotal为单位体积材料屈服时对应的储能极限定值，Wd（T）和WT（T）分别为T温度下的弹性形变能和储存的热能，K为等效系数。进而李卫国等［12，20］首次建立了如下适用于宽温域下无需拟合参数的屈服强度理论分析模型：

式中，σy(T)为T温度下材料的屈服强度，ν(T)和E(T)为材料的温度相关性泊松比和弹性模量，σy(T0)、E(T0)和ν(T0)分别为任意一个参考温度T0下的屈服强度、弹性模量和泊松比，cp(T)为材料的温度相关性定压比热容，Tm为材料的熔点。该模型得到了实验的很好验证［12］。基于此模型［式（2）］，考虑低温下的相应机制，李卫国课题组对高熵合金低温屈服强度进行了评价并与实验结果吻合的很好，同时，在上述分析模型［式（2）］基础上，李卫国课题组系统地研究了控制金属材料屈服强度的各种机制及其随温度的演化规律，构建了可考虑应变率、细晶强化、相变、晶界滑移、固溶强化等机制及其组合影响的系列理论模型［12-13，15］，实现了对各项强化机制的解耦分析。鉴于室温下屈服强度易获取，温度相关性弹性模量可以通过非破坏性实验方便地获取，且弹性模量的某些测量方法不受样品尺寸局限，可在位测量、简单方便、测试费用低，故基于此工作可制造出一种简单、有效的能对不同温度下服役中材料屈服强度在线无损测量的测试设备，为材料屈服强度的在线无损测量与实时监控提供了一种新技术和快速评价方法［12］。

1.2 金属材料温度相关性临界分切应力快速评价方法

临界分切应力（CRSS）是晶体材料滑移系开动所需的最小切应力，其数值大小体现了材料抵抗塑性变形的能力［21］。多晶体材料屈服临界分切应力不仅能够反映材料本身的强度，而且利用屈服临界分切应力还可以预判多晶体材料力学性能各向异性规律［21］。临界分切应力对温度有非常明显的相关性。开展晶体材料的温度相关性临界分切应力理论表征模型研究，对研究不同温度下多晶体材料的力学性能具有重要意义。

基于力-热能量密度等效原理［11］，李卫国、麻建坐等［17］提出以下假设：金属中位错滑移开动时对应单位体积存储的能量存在一个最大值，这个最大能量包含弹性变形能和热能，弹性变形能与相应热能之间存在一个等效关系，并建立了金属材料温度相关性临界分切应力理论分析模型［17］：

式中，τc(T)为温度相关性临界分切应力，G(T)为材料的温度相关剪切模量，τc(T0)和G(T0)分别为任意一个参考温度T0下的临界分切应力和剪切模量，cp(T)为材料的温度相关性定压比热容，Tm为材料的熔点。可以看出，模型［式（3）］无任何拟合参数。模型建立了不同温度下临界分切应力与任意参考温度下临界分切应力、定压比热容和剪切模量之间的定量关系。在式（3）中，定压比热容可以在材料手册中找到，温度相关性剪切模量可以通过实验或材料手册容易获得。基于该模型［式（3）］，通过易获取参考温度下的临界分切应力及不同温度下的剪切模量可以方便快速地评价不同温度下的临界分切应力，如图1所示［17］。

图1 纯Cu在4.2～500 K下的临界分切应力预测值与实验值［22］对比［17］Fig.1 Comparison between the predicted value and experiment data［22］of CRSS for pure Cu from 4.2 K to 500 K［17］

1.3 金属玻璃温度相关性压缩屈服强度快速评价方法

基于力-热能量密度等效原理［11］，李卫国、张先贺等［20，23］对于金属玻璃（BMGs），提出了对应剪切变形区（STZ）失稳时的临界屈服能量密度准则［20，23］，建立了不同温度下BMGs压缩屈服强度分析模型［20，23］：

式中，σC（T）和σC（T0）分别为温度T和T0下BMGs 的压缩屈服强度，γc(T)和γc(T0)分别为温度T和T0下临界剪切应变，fg=G（Tg）∕G（0），即BMGs 在玻璃化转变温度Tg和0 K 下剪切模量的比值，可以取作常数0.85［24］，cp(T)为定压比热容。利用德拜模型可以计算模型［式（4）］中BMGs的定压比热容cp(T)［20，23］：

式中，N、kB和θD分别为阿佛加德罗常数、玻尔兹曼常数和德拜温度。θD可由式（6）获取［25］：

式中，h和V分别为普朗克常数和摩尔体积，ρ、B和G分别为常温下密度、体积模量和剪切模量。

利用模型［式（4）］对Zr41.25Ti13.75Ni10Cu12.5Be22.5、Zr50.7Cu28Ni9Al12.3、Zr60Ni25Al15等BMGs 的低温压缩屈服强度的预测评价结果与实验结果［26-28］对比如图2所示［20，23］。结果表明，预测评价结果与实验数据吻合较好，且参考温度的选择不影响模型预测的结果，因此基于模型［式（4）］可以利用易获取的室温下的BMGs 压缩屈服强度方便地评价低温下的压缩屈服强度。

图2 不同温度下BMGs压缩屈服强度理论结果与实验数据［26-27］对比［20，23］Fig.2 Comparison of theoretical results and experiment data［26-27］of compressive strength for BMGs at different temperature［20，23］

2 材料低温下弹性模量快速评价方法

2.1 金属材料低温下弹性模量快速评价方法

在力-热能量密度等效原理［11］的基础上，李卫国、寇海波等［14，29］建立了块体材料不同温度下弹性模量理论模型：

式中，E（T）和α（T）分别温度相关性弹性模量和线膨胀系数［α（T）可以从手册［30］中查到］，定容比热容cv（T）和熔点Tm可以从手册［31］中查到，熔化热ΔfusH可以从手册［32］中查到，E（T0）为任意参考温度下的弹性模量。不同温度下金属材料的弹性模量、弹性常数和剪切模量均可由模型［式（7）］评价［14，29］。

以弹性常数为例，低温下模型预测结果和实验值对比如图3和图4所示［14，29］。

图3 低温下金属材料弹性常数理论预测值（线）和实验值（点）［33-38］对比［14，29］C11′= 0.5(c11 + c12 + 2c44)，C′= 0.5(c11 - c12)，C = c44，and C11 = c11Fig.3 Comparison of theoretical results（line）and experiment data［33-38］（symbols）of elastic constants at low temperature［14，29］C11′= 0.5(c11 + c12 + 2c44)，C′= 0.5(c11 - c12)，C = c44，and C11 = c11

图4 Cu、Au、Ag弹性常数理论预测值（线）和实验值（点）［39-41］对比［14，29］Fig.4 Comparison of theoretical results（line）and experiment data［39-41］（symbols）of Cu、Au、Ag［14，29］

此模型为预测不同温度尤其是极低温下弹性模量提供了一种新的方法。

2.2 金属玻璃低温下弹性模量快速评价方法

基于力-热能量密度等效原理［11］，李卫国、张先贺等［20，23］建立了BMGs温度相关性弹性模量模型［23］：

式中，E（T）为温度相关性弹性模量，E（0）为0 K 下的弹性模量，德拜温度θD可通过式（6）计算得到。利用此模型［式（8）］，多种BMGs剪切模量、弹性模量的模型评价结果（实线）与实验值（点）［42-44］对比如图5所示［20，23］。计算中相关参数可在文献［44］中找到。模型预测结果与相关学者研究结果［45-46］及实验数据相吻合。因此，模型［式（8）］能很好地预测评价BMGs不同温度下特别是极低温下的弹性模量。

图5 多种BMGs剪切模量、弹性模量随温度的变化规律［20，23］，实验数据来自文献［42-44］Fig.5 Shear modulus G and Young’s modulus E as a function of temperature for BMGs［20，23］，the experimental data are from literature［42-44］

3 材料低温下理想拉伸强度快速评价方法

固体的理想拉伸强度是材料在没有缺陷（如位错、裂纹和杂质）时所能达到的最大拉应力。基于力-热能量密度等效原理［11］，李卫国、成天宝等［47］针对单晶材料在不同温度下拉伸失效时提出了温度相关性临界失效能密度准则（CFEDP）和温度相关性临界应变准则（CSP）［47］。

采用CFEDP失效准则，主应力方向与（x，y，z）坐标轴平行时，李卫国、成天宝等［47-48］建立了不同温度下对任意［hkl］方向的立方单晶单轴理想拉伸强度模型：

式中，σ[hkl]t（T）和E[hkl]（T）分别为温度相关性理想拉伸强度和任意晶体学方向弹性模量，cp（T）为定压比热容。σ[hkl]t（T0）和E[hkl]（T0）分别为任意温度下理想拉伸强度和任意晶体学方向弹性模量，ΔHM为融化热，Tm为材料熔点。

采用CSP失效准则，主应力方向与（x，y，z）坐标轴平行时，李卫国、成天宝等［47-48］建立了不同温度下对任意［hkl］方向的立方单晶单轴理想拉伸强度模型：

式中，εth（T） =α（T）（T-T0），α（T）为线胀系数。

以上两个模型［式（9）］与［式（10）］的预测结果与其他学者的计算结果［49-53］对比如图6所示［47-48］。可以看出第一性原理分子动力学（AI MD）方法存在较大偏差，故低温下理论模型［式（9）］与［式（10）］预测的理想拉伸强度更合理。

图6 不同温度下单轴理想拉伸强度Fig.6 Uniaxial ideal tensile strength at different temperature

4 材料低温下硬度快速评价方法

基于金属材料温度相关性屈服强度模型［12］，结合金属硬度与屈服强度之间存在的关系［54］，李卫国、徐念东等［55］建立了温度相关性硬度理论模型：

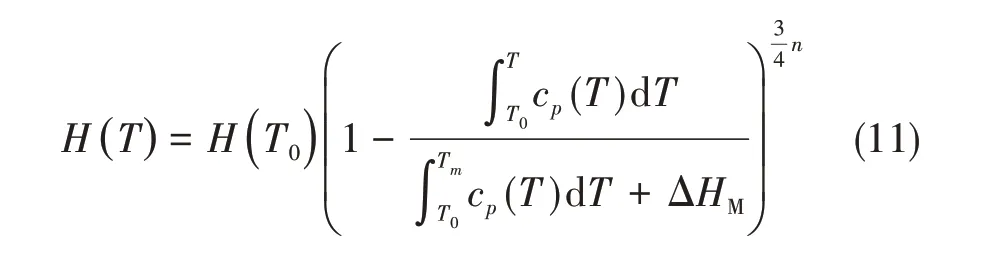
式中，H(T)为温度相关性硬度，H(T0)为任意参考温度下的硬度，参数n可以通过再选择一个参考温度T1下的硬度值H（T1）反推获取。模型中的定压比热容（cp）在室温至熔点的温度范围可以直接通过查询材料手册获取［56］，模型预测结果与实验值对比如图7所示［55］。从图中可以看出模型预测结果与实验值取得了很好的一致性，且当温度接近绝对零度时预测结果曲线斜率趋近于零，符合热力学第三定律。而Ito-Shishokin 模型［57］与Westbrook 模型［58］预测的硬度值随着温度接近绝对零度而急剧增加，这显然是不合理的。这也说明Ito-Shishokin 模型与Westbrook 模型不适用于外推预测金属材料在不同温度下的硬度。模型［式（11）］可对绝对零度到熔点这一宽温度范围的硬度进行很好地预测与评价，高温下硬度实验值与预测值对比可见文献［55］。

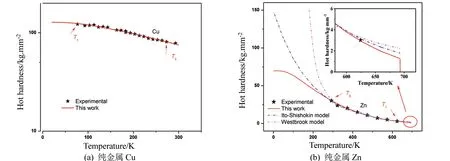
图7 室温以下纯金属Cu［59］和纯金属Zn［60］的硬度随温度的变化Fig.7 The temperature-dependent hardness of Cu［59］and Zn［60］at temperatures below RT

5 材料低温下物理性能快速评价方法

通过建立不同形式相关联能量间的等效关系，赋予力-热能量密度等效原理中各能量项不同的物理意义，李卫国等［11］将提出的力-热能量密度等效原理成功拓展应用于半导体材料、磁存储材料等的温度相关性物理性能理论表征，为低温下半导体材料、磁存储材料物理性能的快速评价开辟了新途径。

5.1 半导体材料低温下带隙能快速评价方法

带隙能是半导体材料中一个非常重要的电学物理量。基于力-热能量密度等效原理［11］，李卫国、耿培基等［8］将考虑温度对材料性能影响的建模思想应用到半导体材料中，从能量等效的角度，建立了如下温度相关性带隙能理论模型［8］：

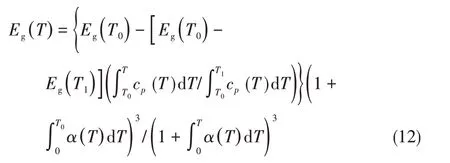
式中，Eg(T)是温度相关性的带隙能，Eg(T0)和Eg(T1)是任意两个参考点T0和T1的带隙能，cp(T)是温度相关性定压比热容，α(T)是半导体材料的温度相关性线膨胀系数，该模型［式（12）］同时考虑了两个主要因素（晶格膨胀和声-电相互作用）对带隙能的影响。模型预测结果与实验值对比如图8所示［61-70］。该模型［式（12）］可以很好地预测半导体材料低温下的带隙能，为确定不同温度下半导体的带隙能提供了一种简便的方法。

图8 温度相关性带隙能理论值（线）与实验值（点）对比Fig.8 Comparison of theoretical results（line）and experiment data（symbols）of temperature dependent band gap energy

5.2 半导体材料低温下折射率快速评价方法

折射率在表征半导体材料的光学特性中起着非常重要的作用。李卫国、耿培基等［9］建立了可综合考虑红移和温度影响的折射率模型：

式中，n(T)为T温度下的折射率，n(T0)为参考温度T0下的折射率，α(T)为材料的线胀系数，Eg(T1)为T1温度下的能带，Eg(T0)为T0温度下的能带，cp(T)为温度相关性的定压比热容，可以方便地从现有文献中查到。模型预测结果如图9所示，模型预测结果和现有的实验结果［72-75］取得了非常好的一致性。该模型利用一个容易获取的参考点就可以简单方便地预测不同温度下半导体材料的折射率，为不同温度下半导体材料折射率的预测提供一种简单方便的方法。

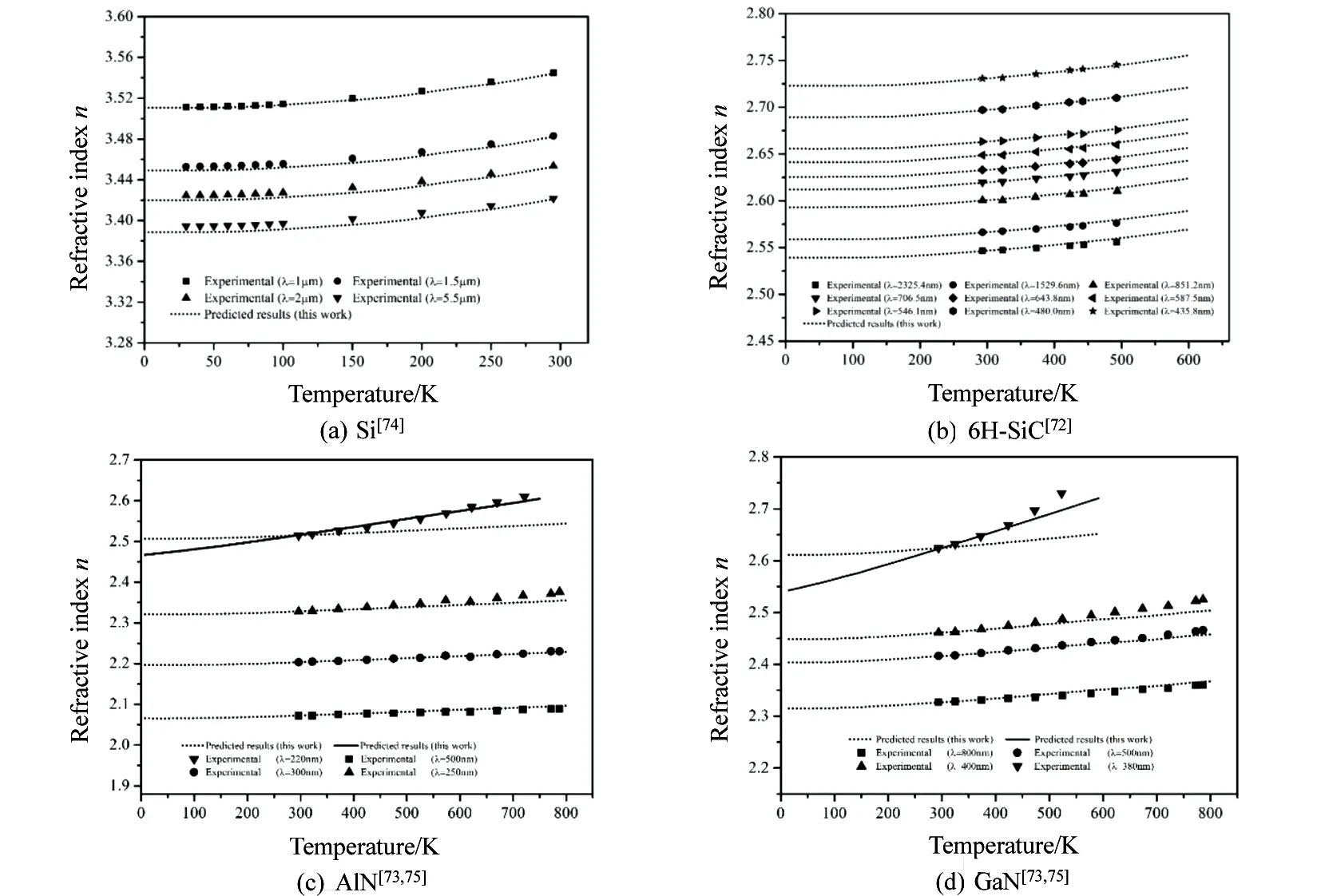
图9 温度相关性折射率理论值（线）与实验值（点）对比Fig.9 Comparison of theoretical results（line）and experiment data（symbols）of temperature dependent refractive index

5.3 半导体材料低温下拉曼频移快速评价方法

半导体材料中，原子的振动行为对研究其非线性光学和电学性质是有重要意义的，例如电子-声子耦合，声子-光子相互作用，声子传输、热传导和热稳定性等。研究不同温度下半导体材料的拉曼频移是非常必要的。基于力-热能量密度等效原理［11］，李卫国、张续耀等［76］假设热能与拉曼频移之间存在定量的等效关系，建立了可计及温度影响的半导体材料拉曼频移模型［76］：

式中，ω(T)为温度T下的拉曼频移，ω(T0)为参考温度T0下的拉曼频移，cp(T)为温度相关性的定压比热容，可以方便地从现有文献中查到，TB为材料的沸点，ΔHM为材料的熔化热，ΔHB为材料的汽化热。模型预测结果如图10所示［76］，模型预测结果和现有的实验结果［77-78］取得了非常好的一致性。该模型［式（14）］揭示了半导体材料拉曼频移和材料沸点、熔化热、汽化热以及热熔之间的内在联系。利用一个容易获取的参考点就可以简单方便地预测不同温度下半导体材料的拉曼频移。

5.4 材料低温下磁晶各向异性常数快速评价方法

磁性材料作为一种功能材料，在现代科学技术中起着至关重要的作用［79］。磁晶各向异性能常作为衡量在信息科学领域有着广泛应用的磁存储材料和磁致伸缩材料宏观磁性能的重要指标［79］。在科学研究中通常利用磁晶各向异性常数来表征磁晶各向异性能。大量研究结果表明温度对磁晶各向异性常数有很大影响［80-82］。因此，研究磁晶各向异性常数随温度的演化规律能为磁性功能材料的设计和应用提供理论依据［79］，具有重要的意义［83］。李卫国、董攀等［10］将力-热能量密度等效原理［11］拓展应用于温度相关性磁晶各向异性常数的理论表征，假设单位质量材料存在由内能和磁晶各向异性能组成的最大储能极限，同时，磁晶各向异性能与内能之间存在等效关系，建立了如下温度相关性一阶磁晶各向异性常数理论表征模型［10］：

式中，K1（T）为温度相关性一阶磁晶各向异性常数，K1（T0）和K1（T0）分别是参考温度T0和T1下的一阶磁晶各向异性常数，β（T）是温度相关性体膨胀系数，cP(T)是温度相关性定压比热容。模型所需的定压比热容、体膨胀系数容易从材料手册或其他文献中获取。模型预测结果与实验值对比如图11所示，模型预测结果与实验结果吻合很好，为预测铁磁性金属在不同温度下的一阶磁晶各向异性常数提供了一种实用方便的途径，避免了在极低温度下实验的困难。

图11 温度相关性一阶磁晶各向异性常数理论值与实验值对比Fig.11 Comparison of theoretical results（line）and experiment data（symbols）of temperature dependent first order magnetocrystalline anisotropy constant

6 总结与展望

综上所述，利用力-热能量密度等效原理，已经对深空极低温服役环境下材料屈服强度、弹性模量、临界分切应力等力学性能；半导体材料的带隙能、折射率、拉曼频移，金属材料磁晶各向异性常数等物理性能进行了很好的表征和低成本快速评价。为实现地面实时监测在轨航天器中关键材料的主要力学、物理性能提供了有效途径，为国家高端技术装备建设中关键材料的设计、可靠性评价和实时性能监测等提供重要的手段。后续的研究工作可以从以下几个方面入手进行考虑。

（1）系统研究并表征不同低温环境下复合材料的弹性模量、强度及失效破坏模式，考虑温度、基体微裂纹、界面损伤、低温热循环和冷却速率等因素对复合材料性能参数如变形、失效强度和渗漏率等非线性影响，建立具有深刻物理背景且适用于不同服役环境的低温复合材料力学性能理论表征方法。

（2）在极低温复合材料性能预测方面，选取合适的方法来建立高效可靠的评估模型，以便提供低温复合材料力学性能快速评价的方法，促进实现低温复合材料从基础研究向应用研究的转变。

（3）利用力-热能量密度等效原理，通过不同超常环境下相对应的其他形式能量的等效方式，也可拓展应用于超高∕低温、热冲击、高热流、强辐照、极高真空、超高压、强磁场、强化学环境、高过载和高应变速率等及其组合更广泛超常环境下材料服役行为的理论表征和评价，解决更广泛领域面临的问题，为我国高端战略装备的发展提供理论支撑和技术支持。