基于半翻转课堂的混合教学模式下数值分析课程的建设

谭志军 江颖 吴静文 陈健军

摘  要：文章根据数值分析课程的教学特点，构建并详细阐述了符合课程特点的基于半翻转课堂的混合教学模式。对于不同学习阶段的学生，针对不同的着重点进行分层教学。在整个教学过程中，坚持以“教师为主导、学生为主体”的理念，充分发挥线上教学和线下教学所带来的优势，从而提高学生自主学习的积极性，提升教师教学的质量。

关键词：数值分析;混合教学模式;分层教学;半翻转课堂

中图分类号：G640 文献标志码：A          文章编号：2096-000X（2021）34-0071-05

Abstract： According to the teaching characteristics of numerical analysis course， this paper constructs and expounds in detail the hybrid teaching mode based on the semi-flipped classroom. For students at different learning stages， stratified teaching mode is carried out according to different emphases. In the whole teaching process， the mode adheres to the concept of "teachers as the leading and students as the main body" and make full use of the advantages of online and offline teaching， which improves the students' learning enthusiasm and the quality of curriculum teaching.

Keywords： Numerical Analysis; mixed teaching mode; hierarchical teaching; semi-flipped classroom

由于新冠肺炎疫情的影响，在这一两年内，各大高校均采取过线上教学模式，使无法到校的学生能够按时上课，顺利毕业。现在国内疫情情况有了好转，学生们都能够坐在课堂里上课。通过两种教学模式的实施，我们发现传统线下教学与网络教学各有其优缺点。传统线下教学采用的是线下面对面教师讲授为主的教学模式，这种模式能够有效观测到学生的学习状态，但所教授的知识点局限于课本。虽然线上教学时间地点灵活，资源丰富，但是在此模式下学生的学习效果与学生的学习状态都缺乏有效的监督与管理。因此，对数值分析课程改革迫在眉睫，新时代的背景下数值分析课程的教学设计必须将理论和实际相结合，着重设计完善学生的知识体系、动手能力的课程模式，这对于提升教师教学质量、提高学生的兴趣，对数值分析的课程建设有深远意义。

一、新教学模式

（一）混合教学

混合教学方式将线上教学与传统线下教学有效结合在一起，培养学生自主学习的习惯，促进线下课堂教学质量的提升，增加教学方式的多样化。

20世纪90年代随着计算机的发展，数字化学习被国外众多学者提出并基于此构造了线上线下相统一的混合教学模式，在发展一段时间后由于国外学者的理念冲突，导致数字化學习在2001年前后进入低潮之后，国外教育学者在吸取前一时代的经验后，在设计教学模式的过程中考虑将网络学习、传统学习两者相结合并依托互联网远程通信的快速发展，从而构造出与数字化学习模式不同的在线教学与传统线下课堂教学相结合的新型教学模式。此教学模式在当时被誉为是“最有效的教学形式”。之后，以慕课为依托，线上线下互相结合的混合教学方式又得到了极大发展。顺应这个趋势，国内原打算实施国外20世纪90年代的传统网络教学模式，但进入21世纪，我国与国外沟通加深，国内学校了解混合教学模式的进展后，结合自身情况在课程大纲准备和教学实施过程中不断向混合教学模式转化。这一跨世纪的教学改革给国内高校带来深远的影响;首先由国内顶尖高校带头采用混合教学方式来开展思政课进而普及到其他普通院校。

目前形成的混合教学方式主要包含两个教学部分，一是课前、课后的线上教学模式，学生利用课余时间，通过网络教学平台如微课、慕课等提前学习相关知识点完成初级阶段的学习目标;学习完网上课程后，学生通过网络教学平台完成复习、作业以及利用网络优势深入了解课题。二个是线下教学模式，主要是师生线下面对面授课方式，老师能有效掌握学生的学习情况，学生也能更好地与老师沟通交流。混合教学方式是教育改革的一次有力尝试，其依靠网络信息快捷传递的优势，将教育资源进行优化重组，并传递到各个角落，真正摆脱传统教育受时间与空间的局限性，进一步实现教育公平化、多元化、科学化[1]。

（二）半翻转课堂

半翻转课堂为翻转课堂的进一步发展，其解决了翻转课堂的一些不确定性因素。在翻转课堂中微课作为课前学习环节里的重要载体，是翻转课堂模式能否有效开展的重要先决条件，其作用、地位不言而喻。但是，在使用翻转课堂进行课堂教学的一个重要条件为：学生自身需具备不俗约束能力和自学能力，而这只是一种理想的研究基础。实际上，学生个体在成长过程中因环境不同，将产生巨大的差异。在独立学习的环境中，被动自制力差的学生会在无人约束情况下将用来学习微课视频的课前时间，通过打游戏等娱乐方式而消耗;或者因为不良学习风气的影响以及其他学科的过重负担也无法正常开展学习。学生整体的自觉性达不到研究者预期的理想情况，以此作为基础研究对象的研究势必无法实现预期的效果。因为研究群体具有如此高的不确定性，翻转课堂很难实现真正的翻转。所以，以微课为核心的翻转课堂并没有给人带来惊喜的效果，成效甚微，不能被广泛应用到教学实践中。因此，半翻转课堂模式应运而生。

半翻转课堂的教学模式是翻转课堂的改良，由翻转课堂的纯微课学习转换为：课堂讨论和新知识授课两部分，分别由学生和教师主导，能够使学生加强线上、线下活动的结合，提升课堂参与感，提高学习主动性、兴趣性[2]。传统教学是以教师讲授，学生倾听的模式开展。在半翻转课堂的设计中，学生通过课前学习，小组讨论可以向教师提出问题。合理设计课程，发挥学生的主观能动性，引导学生合作学习，在适当时候教师进行答疑并强调重点。

二、数值分析课程的教学特点

数值分析课程主要内容为：以科学计算为核心，通过各种数学问题数值求解计算方法来呈现科学计算和数学在实际场景应用的课程，目前该课程在国内外大学理工科专业中普遍开设。在时代的变迁中科学计算已经成为现代工业的一个重要工具，科学计算已成为科学研究、管理经济、工程技术等领域的必要部分，因此，对于数值分析的研究和应用已经扩展到自然科学、经济和工程技术等多个领域;然而数值分析是一门建立在数学分析、高等代数、矩阵分析等数学基础课上，研究数学问题近似解并利用计算机技术进行验证与实现的综合性学科。数值分析已经成为高等学校理工科的一门重要课程，综合了分析、代数、方程等数学理论与其他相关数学课程相比它更偏重于应用，但课程中所提到的基础理论和方法已经在其他专业课程中运用，甚至在解决实际问题中也常常会用到，其内容包括有数值代数、数值逼近、微分方程数值解等结构比较松散的理论知识，因此在教学过程中我们既要让学生体会到数值分析课程在数学理论上的逻辑性和抽象性，更要让学生体验到在掌握数值算法基本原理的前提下设计算法编程求解具体数学问题的实践性。

（一）数学理论的特点

数值分析课程的内容主要包含如下几个部分：误差分析、 数值逼近、数值微积分、线性方程数值解法、非线性方程数值解法和微分方程数值解等。虽然数值分析中的许多理论知识是在高等数学中已经学习过，但是与单纯的学习理论分析不同，数值分析的理论知识更注重运用理论知识构造并分析数值算法。比如，利用微积分原理分析对Lagrange插值多项式进行误差分析、利用Taylor 级数构造差商型数值微分公式、运用矩阵分解理论构造追赶法求解线性方程组、利用Taylor展式构造并分析常微分方程初值问题的数值解法、在sololev空间下利用green公式将微分方程边值问题转化为与之等价的变分问题，再基于变分问题导出有限元法[3]。由上述例子可以看出，数值分析中涉及的理论知识点是由许多不同的数学基础知识组成的，结构比较松散。

（二）数值实验的特点

虽然数值分析中的理论推导是抽象的，但是由理论推导出来的数值公式都可以通过编写代码在计算机上实现并用于求解具体的问题。在计算机上进行数值实验让学生能够感受到科研的乐趣，培养学生实际动手能力与探索能力。在实际教学中，除了教材中列出的数值算例，还可以根据教学内容选取一些简化的实际问题鼓励学生运用数学建模知识建立数学模型，利用所学的数值方法借助编程语言求解数学模型。由此可发现数值分析既含有纯数学的高度抽象性与严密科学性等特点，又有广泛性与实用性相结合的高度技术性的特征。因此，在实际教学的内容组织上，应兼顾该课程具有理论性和实践性的特点，采取以下步骤进行教学：（1）实际问题;（2）数学问题提法及存在性;（3）方法构造性;（4）算法的收敛性及稳定性。采取以上步骤的同时强调，数值分析此门课程中最重要的三个思想：近似思想、迭代思想、离散化思想。数值分析作为一门实践性强的数学方法课程，實验内容必不可少，具体部分可以分为三个层次：上机实习（学会常用编程语言，完成配套的基础实验题）、课程设计（利用数值方法解决较复杂和应用性问题）、数学建模（利用数学知识，求解较复杂和较强应用性的实际问题）[4]。

数值分析常用的软件为Matlab软件，它是一个用于数值计算、图形处理和符号计算等科学计算的系统环境，其主要特点之一就是将高性能的数值计算和结果可视化有机融合，为在数值分析课程教学中实现数值计算、动画演示教学和动态数据分析要求提供了可能[5]。在教授数值分析课程的同时还需引导学生掌握Matlab的使用方法。

三、分层教学

分层教学课程就是教师确定班级学生现有的知识、能力水平和学习潜力，并将全体学生通过某些标准科学地分成若干发展水平相近的学习小组，在教师分层策略以及成员的相互作用中这些小组的成员能在课堂上得到符合自身的发展和提高，以上的分组教育学者称之为分组教学、能力分组，其主旨是将学生按照过往学习中所展现的学业水平、知识接受度的不同进行科学分组，教师根据不同小组的实际水平安排不同的学习任务以及学业目标。分层教学要将学生进行科学的分层，根据学生不同的水平，分为不同的目标层次，对不同目标层次的学生，教师需采用不同的学业目标以及教学目标。评价分层：不同层次采用不同的考核方法。分层教学理念是因材施教观念的具体表现，充分发挥了教育内涵。在分层教学的过程中，针对本课程只是更新快、信息量大、教学学时少等特点，采取半翻转课堂教学模式达到更好的教学效果。总的原则是教学形式基本相同，即教材相同、课时数相等、进度一致、教学手段基本统一，不同之处是对各个层次的深度要求不同，从而带动全体学生积极参与学习[6]。

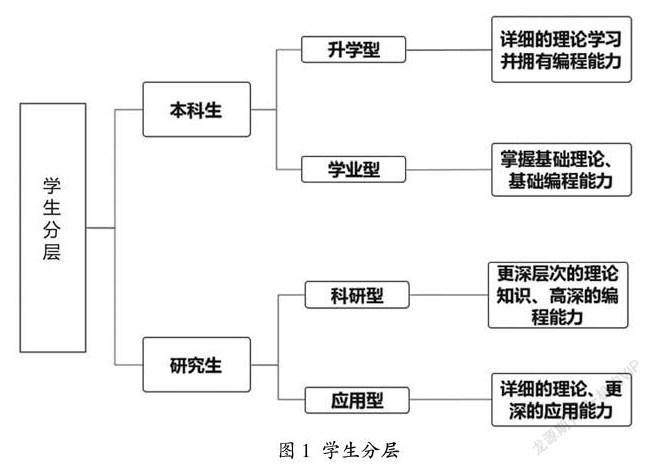
根据数值分析课程的特点，对于本科生与研究生，需要有不同的侧重点，于本科生以及研究生中不同层次学生也要有不同的针对点。在针对本科生教学时，应注重理论的讲解，培养学生理论分析的能力，为算法的学习打好基础。对于研究生而言，应着重培养他们进行数值实验的能力。在设置问题时，采用简单、中等难度的习题和数值实验。对于本科生，理论练习的题目应多于数值实验的题目;对于研究生，应选取较多的数值实验的题目。具体分层如图1所示。

（一）本科生分层

由于数值分析课程一般开设于本科三年级阶段，则针对本科生，根据其目标分层大致将其分为两组，分别为：升学考研组以及完成学业组。

对于考研升学组：此类学生通常需要对该课程进行深入的学习，因此此类学生的目标力求知识点讲授得清楚，同时在教学中也进行数学史的介绍，让学生了解一些该学科的发展过程，并且培养学生的理论推导能力与自主学习能力。

对于完成学业组：此类学生通常只需完成该课的学习任务，因此，对此类学生的教学内容，要在注重各部分知识点的基础上，介绍其背景及应用范围。同时，针对教学培养的目的，还应将培养学生自主建模解决实际问题的能力纳入其中。

（二）研究生分层

在研究生与导师取得联系确定基本方向后，应遵循研究生意愿的基础上，将研究生分为两大类进行分层培养：其一是对学术拥有浓厚兴趣，并立志走向科研方向的学术型研究生，其二则是对实际应用颇感兴趣，倾向于将自身所学用于工程实践的应用型研究生。在研究生确定以上两种不同分类后，需要随着时间的推移、时刻关注学生的后续学习和研究情况进行动态调整。在培养过程中对于科研为导向的学术型研究生：学生需要对该门课拥有更深层次的理解，能对现有知识进行升级、推导新的知识，并应用到更广的内容里去;对于工程实践为主的应用型研究生：学生需要对此门课所讲述的方法进行深层次的应用。研究生的分层培养将不同类型的学生按照各有侧重的培养方案进行培养，使其在研究生的学习生涯中获得未来工作或科研相关的能力，充分发挥各自的特长。因此，对于两种类型研究生的课程教学调整是十分必要的，这样能使学生更好的学习，并对学生进行更深层次的科研或参加应用性较强的工作大有帮助。然而，由于现阶段各高校的客观条件有所限制以及主管单位在培养中的不充分重视，导致大部分科研型研究生和应用型研究生的培养方案并没有得到区分，而此做法必然会影响研究生的培养目标，从而导致研究生培养质量的下降。因此，针对研究生教育的分类教学改革对于研究生本身的发展及其所在学校的发展都有十分重要的意义。

四、基于半翻转课堂的混合教学模式下数值分析课程分层教学体系的架构

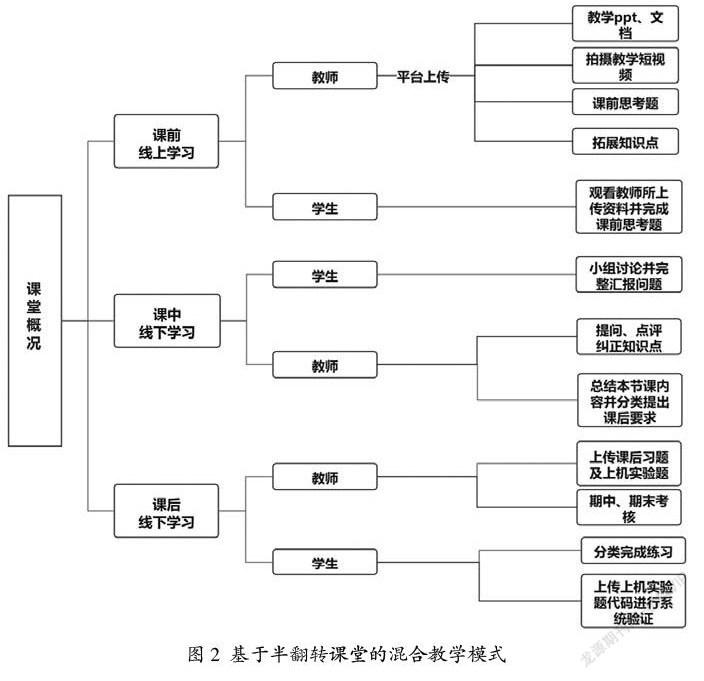
基于半翻转课堂的混合教学主要采用如图2所示的教学模式。下面我们将详细介绍教学模式中的每一个环节。

（一）课前的线上学习

课前为线上学习阶段，此阶段主要依赖教师在教育平台上传学习资料，学生在线自主学习。将本节课所要学习的目标、重难点写入教学ppt或文档中。根据数值分析课程特点，我们通过求解数学模型引入数值算法。比如在插值法这一章节的讲解中，我们根据现代机械工业中用计算机程序控制加工机械零件[7]这一实际问题引入插值法。在拍摄的5～10分钟的微课视频中，教师着重讲解数值方法的构造和应用。如在插值法这一章中，我们首先讲解Lagrange插值多项式的构造与应用，重点讲解基函数的构造。结合Matlab软件展示数值结果如：绘制基函数的图形， 使学生更好地理解Lagrange插值多项式的构造;通过不断增加插值节点的个数，举例让学生体会到Lagrange插值的Runge振蕩现象。随后我们从理论角度解释Runge现象即理论分析插值余项，从插值余项公式分析为何会出现高次多项式插值的Runge振荡现象。设计简单、中等难度的习题和数值实验例子，其中简单难度的习题和数值实验为课前必做题。为了解决数值实验中的算例，教师在所给的文档中需要给出Matlab软件基本的使用方法或者推荐相关参考书。在数值算例的习题中，教师应当给出一定的提示，帮助学生完成代码编写。最后，教师可根据本节的内容推荐相关知识的延伸与应用，例如Lagrange插值多项式在高次插值时出现Runge现象，那又该如何克服Runge现象呢？

（二）课中的线下学习

在线下的课堂中，我们采取半翻转课堂的形式即讨论与授课相结合。平均每5～8人一组讨论课前预习时遇到的困难并由一人在讲台前总结该小组的疑问，其他同学可以帮忙解答。在学生互动结束后，教师根据学生的问题讲解相应的知识点。为确保学生能够全面了解数值分析的理论体系和其思维特点，我们在教学过程中简化了部分数学理论及其证明[8]。对于重点推导，我们需要在课堂进行强调;对于数值实验中的难点，我们需要在课堂上进行解释。

（三）课后的线下学习

课后教师上传中等难度的课后习题。根据课程安排需求，适时上传期中考核、期末考核。学生根据课上的答疑继续完成之前的练习，同时完成课后练习、上传代码、系统验证。

（四）课程成绩的评定方式

根据课程模式的特点和数值分析课程的特点，我们采取如下的评分模式：平时线上成绩占50%，期末理论考试占50%。每次设置线上习题时，教师需要合理安排分数，期中，数值算例在每一章节的分数中占70%，最终平时线上成绩是每堂课的线上成绩的均值。这样的评分方式不仅使学生们能够重视每一次的线上学习，而且能够锻炼学生对数值算法的实际应用能力。

五、结束语

本文针对数值分析课程的教学特点，提出将半翻转课堂与混合教学两者融合的教学模式。对于本科生与研究生，我们分别侧重于理论的讲解和数值实验的练习。在该模式下，课前设置问题，录制相关基本知识点的视频，鼓励学生先独立解决问题，提高学生对线下课程的参与热情和主动性。线下课程中，学生带着问题相互讨论，培养了学生的合作精神，改变了教师先教学生后学的教学模式。通过线上学习、小组讨论、教师的针对性解答和综合性指导， 加深了学生对数值分析中算法构造和重点理论的理解，也培养了他们用数值算法解决实际问题的意识和能力。通过教学实践，多数同学认为基于半翻转课堂的混合教学模式下数值分析课程能提高自身的学习效率，使自己能够带有目的性的去学习，更能让自己充分利用网络资源进行探索性学习。

参考文献：

[1]中共中央宣传部.习近平总书记系列重要讲话读本[M].北京：人民出版社，2016.

[2]郭建，蒲戈光.半翻转课堂的嵌入式系统设计课程混合式教学模式[J].计算机教育，2021（8）：157-160.

[3]张诚坚，覃婷婷.科学计算引论[M].北京：科学出版社，2011.

[4]孙杰宝，张达治，吴勃英.工科研究生“数值分析”课程分类教学改革探讨[J].天津市教科院学报，2018（4）：69-71.

[5]孙智娟，徐杜，钟舜聪.MATLAB在计算机辅助《数值分析》与计算中的应用[J].计算机工程与科学，2002（1）：70-73+107.

[6]张美玲.中职校《计算机应用基础》分层教学实践的研究[D].扬州：扬州大学，2013.

[7]李庆扬，王能超，易大义.《数值分析》[M].北京：清华大学出版社，2008.

[8]宋松和，朱建民，唐玲艳，等.高等《数值分析》课程教学改革探讨[J].高等教育研究学报，2008，31（4）：66-67.