汽车排气系统吊钩位置的不同设计方法研究*

谢华林,龚运息，尧潇雪，黄大伟

(1.广西科技大学 机械与交通工程学院，广西 柳州 545616;2.佛吉亚(柳州)排气控制技术有限公司，广西 柳州 545000)

0 引 言

排气系统是汽车振动分析、噪声分析的重要组成部分之一。它的热端(三元催化氧化器)与发动机相连，冷端(波纹管、消声器、排气尾管等)通过吊钩与车身连接。当发动机工作时，所产生的振动会通过排气系统传递到吊耳挂钩，然后传递到汽车底盘，从而影响汽车的乘坐舒适性。因此，吊钩位置布置是否合理，是对于排气系统能否有效地降低车身的振动，降低车内振动和噪声水平，以及确保进行后续整车NVH的研究的重要前提。目前，国内外学者主要采用平均驱动自由度位移法[1-4]，也就是(ADDOFD)法对排气系统吊钩位置进行设计，但是这种方法在数据处理过程中较为繁琐，其需要关注各潜在节点在不同阶振型下的位移输出与每一阶系统振型。而均方根值(RMS)法相对与ADDOFD法在数据处理上更加简单快速，只需将设计吊点位置函数进行积分求均方根值，找到振动能量最小值点即可。

由此，基于上述两种方法对某车型排气系统悬挂位置进行了设计与对比分析。通过UG和Hyperworks软件建立有限元模型并进行验证，基于ADDOFD法与均方根值法得到了两种方案的吊钩悬挂位置，结合排气系统与整车底盘的安装情况和仿真验证(模态分析、静力分析以及动力响应分析)，确定了吊钩的最终位置，且较为合理地预测了此排气系统的性能，从而为之后整车NVH性能的改善提供了一定的理论依据。

1 排气系统有限元模型的建立

通过UG建立排气系统三维实体模型，然后导入Hypermesh软件中。为了不影响其模型求解精度，减少计算时间，作出了以下结构简化处理[5]。其中，对结构厚度与长度相差太大的组件采取抽中面(midsurface)的方法，将排气系统连接管、消声器壳体、消声器内部进、排气管、隔热板等简化为三角形或四边形的壳体单元；消声器内部穿孔管、隔板上的小孔不予考虑；波纹管使用一个弹簧单元和两个质量点来代替，两端用RBE2刚性单元与连接管道相连。材料为SH409L，弹性模量2.02×105MPa，泊松比0.3，密度为7.72×10-9t/mm3。

设定单元尺寸为5 mm，对该排气系统进行网格划分，法兰之间的连接采用螺栓紧固，可以看成是刚性连接，用RBE2进行模拟连接[6]，剩下的其余部分组件结构之间也使用RBE2进行连接，得到有限元模型如图1所示。

图1 排气系统有限元模型

2 排气系统吊钩位置的设计

2.1 平均驱动自由度位移(ADDOFD)法

假设单点激励，根据多自由度系统模态分析理论[7]，响应点l与激励点p之间的频响函数为：

(1)

式中:φlr为第l个测点、第r个模态振型系统；Mr和ξr分别为模态质量和模态阻尼比。

如果激励力的频率为ωr，则近似地有：

(2)

对于线性系统, 位移响应的幅值和频响函数的幅值成正比, 即

(3)

进一步假设振型以质量矩阵归一化，各阶模态阻尼近似相等，则：

(4)

为预测某个自由度在一般激励情况下 (在某个频率范围所有的N个模态均被激发)位移响应的相对大小, 定义第j个自由度的ADDOFD为：

(5)

2.2 吊钩位置的设计——方案一

在波纹管末端，沿X轴方向每隔50mm选取一个潜在吊挂点位置进行编号，然后利用平均驱动自由度位移法计算，得到排气系统0～200 Hz以内的ADDOFD值，如图2所示。

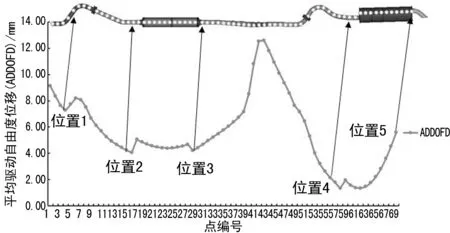
图2 排气系统潜在悬挂点的平均驱动自由度位移结果

结合排气系统的结构和平均驱动自由度位移理论，得到排气系统潜在悬挂点编号，如图2中位置1～5所示的点[8]。由于位置1处于弯管中段，考虑车身结构以及安装情况，所以位移1不作为潜在选取点。因此，最后确定的潜在位置点有4个，分别为图中的位置2、3、4、5。由此可以得到挂钩的设计方案如图3所示。

图3 吊钩位置设计方案1

2.3 均方根值(RMS)理论

均方根值，又被称为方根均值或有效值。在一段时间T内，对于随机信号f(t)，将其所有值平方求和然后再开平方[9]，即：

(6)

自相关函数Rf反映与随机变量在时域范围内特性相关的信息：

(7)

式中：Sf为功率谱密度函数，反映时域范围内的相关信息；ω为信号频率；τ为时间差。

当τ=0时，式(7)可改写为：

(8)

式(6)、(7)和(8)表明，时域范围内的均方根值(RMS)与频域范围内频响曲线下方区域的面积相等，对频响曲线在频域范围内进行积分即可得到时域范围内的均方根值(RMS)。对于振动信号，此均方根值(RMS)可表征系统振动能量的大小[10]。

2.4 吊钩位置的设计——方案二

沿波纹管末端，在X轴方向每隔50 mm选取一个潜在吊挂点位置进行编号，约束排气系统前端法兰除Z向外的所有自由度，并在前端法兰处施加范围为0～200 Hz的Z向激励[11]，得到69个点的Z向频率响应函数。然后通过调用RMS函数对69条曲线在频域范围内进行积分，从而得到各点的振动能量大小如图4所示。

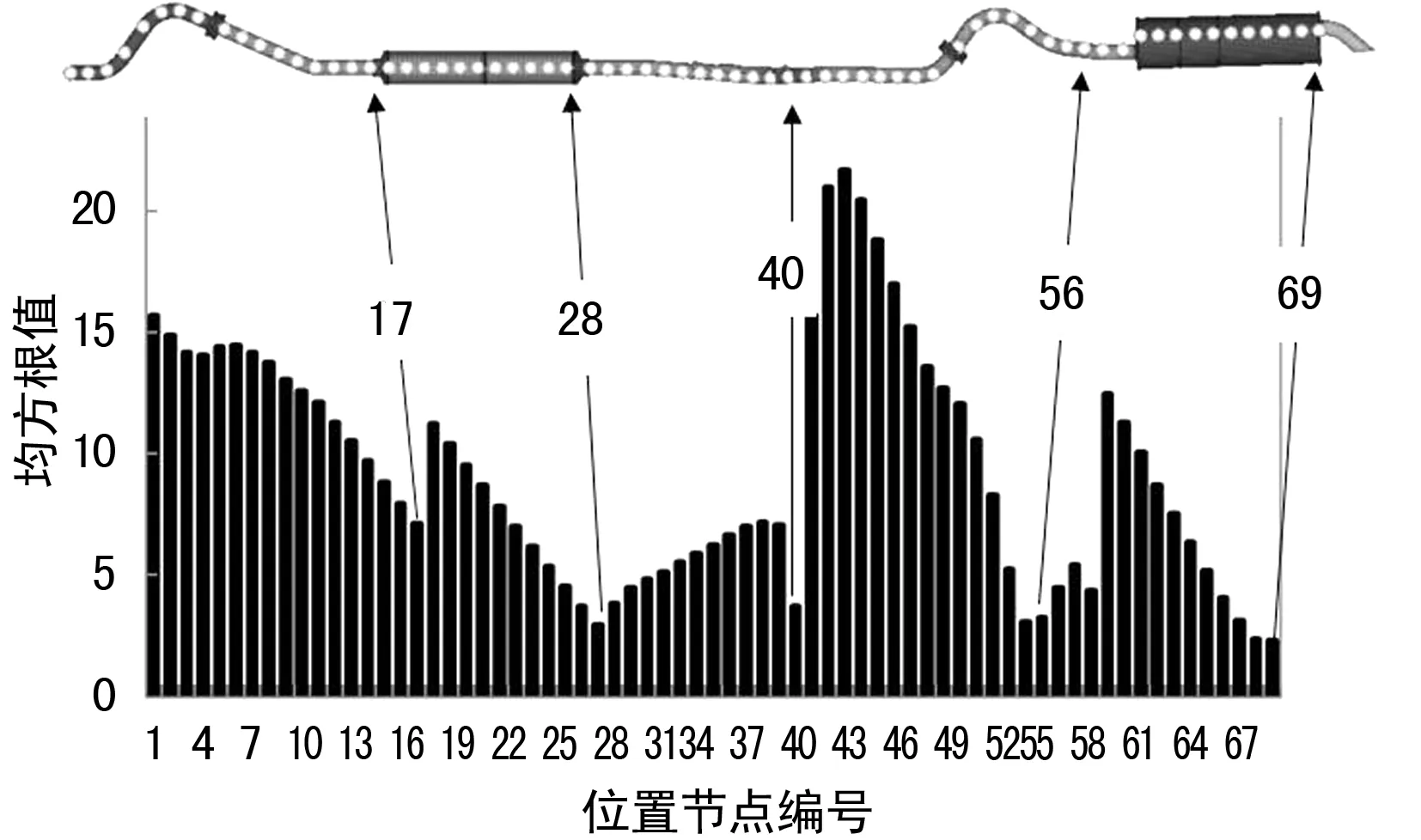
图4 潜在吊钩位置点的均方根值

由方均根值理论我们可以知道，选择振动能量较小的位置放置吊钩比较合适，即图4中位于波谷及波谷附近的点，如17号、28号、40号、56号以及69号点。由于17号点与28号点位置靠的比较近，且它们都属于前消声器总成部分，而17号点位置相对于28号点比较靠前，再结合整体受力情况，很明显可以看出17号点和40号点比28号点和40号点的组合更为合适。最终拟定的设计方案如图5所示。

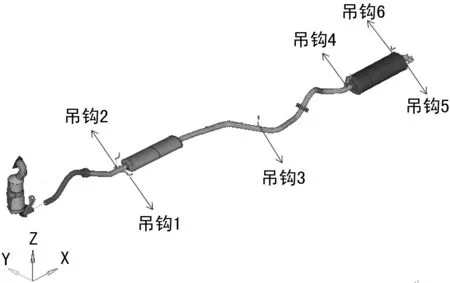
图5 吊钩位置设计方案2

3 两种吊钩方案的设计验证

3.1 约束模态与静力分析

(1) 约束模态分析

对上述两种方案排气系统进行约束模态分析，约束边界条件：约束三元催化氧化装置法兰与发动机悬置点，约束所有车身侧吊钩。吊钩使用六面体实体单元进行计算模型的建立，排气系统悬挂胶采用弹簧连接[12]，排气系统悬挂的刚度在x、y和z方向分别为3 N/mm、3 N/mm和12 N/mm。求解频率范围设置为20～200 Hz, 利用Hypermesh软件中的OptiStruct求解器进行约束模态求解计算，得到两种方案的约束模态固有频率如表1所列。

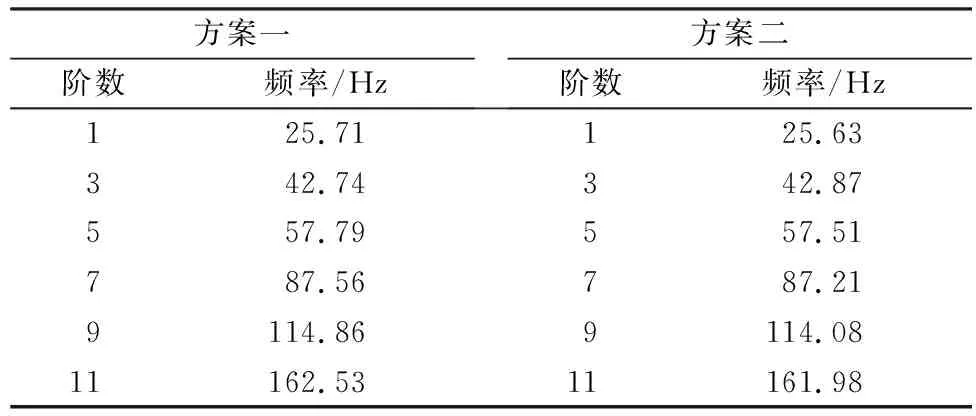
表1 两种方案约束模态分析结果对比

(2) 静力分析

约束三元催化氧化装置法兰和排气系统吊钩位置橡胶吊耳处与车身相连的吊钩端，然后加载重力加速度进行静力分析。从而得到如图6两种方案下的各个被动侧吊钩支反力与图7两种方案下的排气系统整体位移图，以及图8橡胶吊耳的最大位移值。

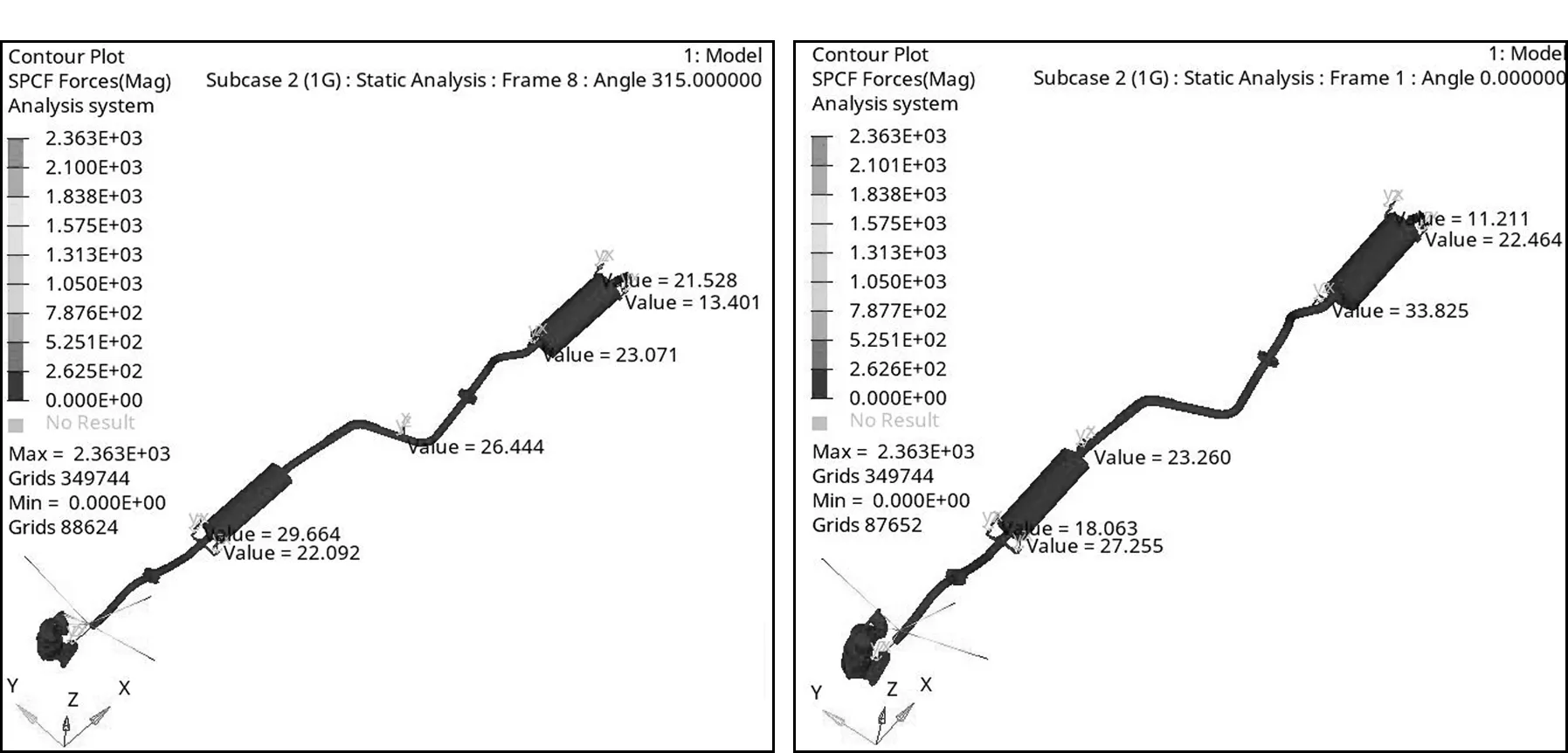
图6 两种方案下的各个被动侧吊钩支反力

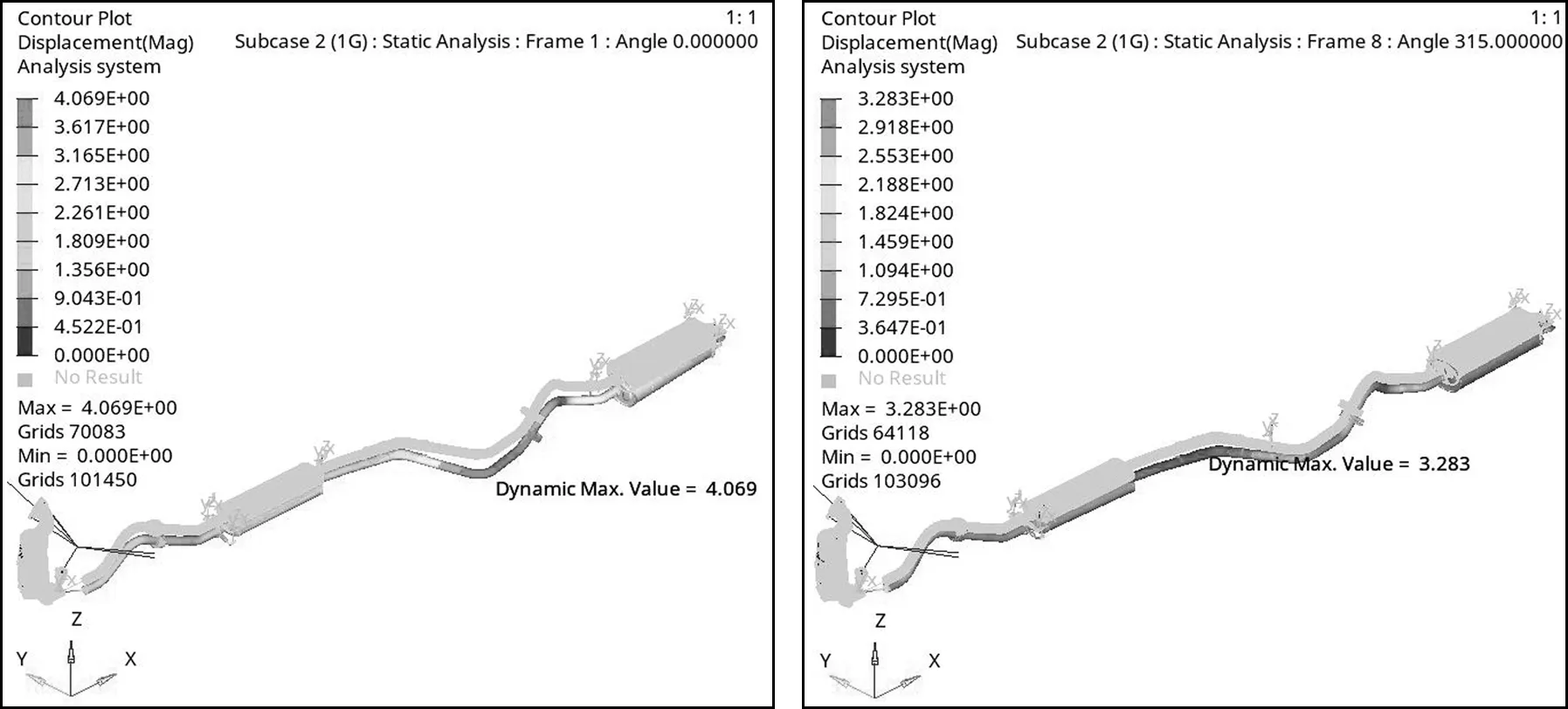
图7 两种方案下的排气系统整体位移图

通过对比两种方案的约束模态以及重力工况下静强度计算情况，得出以下结论。

① 约束模态：在频率20～200 Hz范围下，两种方案的各阶模态值与其相对应的振型图相差不大。

② 静力分析计算：如图7、8可以看出，方案二排气系统的整体位移量比方案一小，且方案2吊钩位置的支反力分布较均匀，最大静应力较小。

③ 两种方案下的四组橡胶吊耳最大位移均小于3 mm，排气系统整体载荷分布均匀，两种设计方案均满足重力载荷下的相关要求。

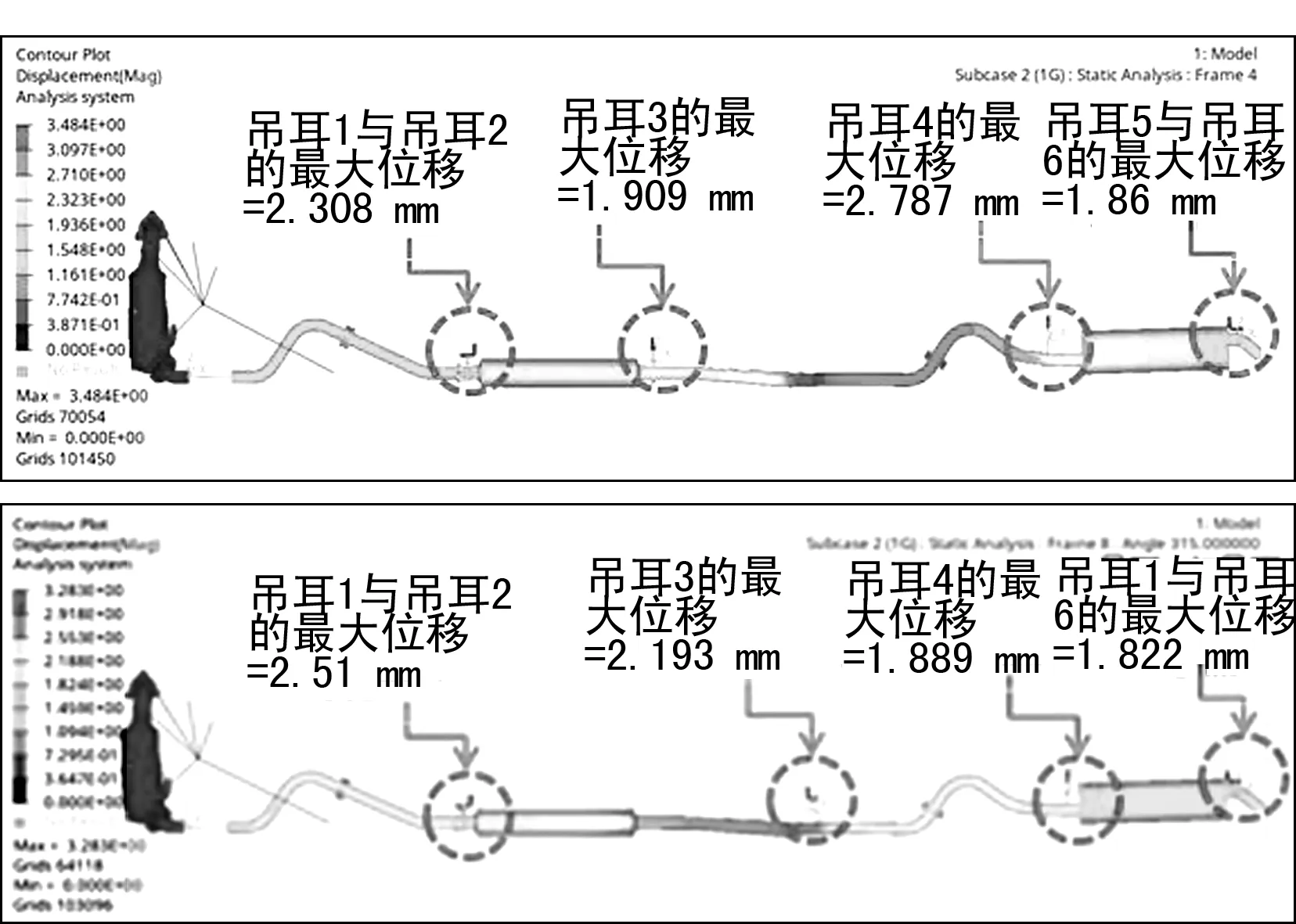
图8 两种方案下的橡胶吊耳位移

3.2 动力响应分析

动力响应分析的目的是分析传递到车体上的力，简而言之就是分析橡胶吊耳上的传递力，对于普通的轿车而言，目标一般不大于10 N[13]。由于受到挂钩受力大小和空间位置的限制，并不是所有挂钩都能处于位移最小值点，所以我们选择两种方案中位置一致的挂钩1、挂钩2和挂钩4作为研究对象。参考企业标准，在发动机质心加载1×105 N·mm的扭矩，激励频率范围在0～120 Hz，得到两种方案下橡胶吊耳的传递力如下图10所示。结果表明，两种方案下的吊钩传递力都小于10 N，满足设计要求。

图9 两种方案下的吊耳传递力

4 结 论

基于ADDOFD法与均方根值法理论基础，通过CAE仿真得到了两种不同的吊钩位置设计方案，并进行了一系列仿真验证，得出以下结论：

(1) 从两种方法确定的吊钩位置计算验证得到：约束模态分析结果相差不大；静力分析方案2的系统最大位移较小且挂钩的支反力较均匀，橡胶吊耳的最大位移量都小于3mm；动力响应分析吊耳传递力都小于10mm；综合来看方案2比方案1更好。

(2) 对于排气系统吊钩位置的设计，均方根值法相较于传统的平均驱动自由度法在数据处理上速度更快，位置点确定较容易，且设计验证都满足排气系统相关设计要求。