圆形压电振子的理论分析与应用研究*

贺春山，李金城，田晓超

(长春大学 机械与车辆工程学院，吉林 长春 130022)

0 引 言

由压电陶瓷材料和金属基板构成的压电振子多用于微小型系统的驱动力源，其具有速度快、体积小、无磁干扰等优点，压电振子振动位移可达到微米级甚至纳米级，变形精度非常高[1-3]。压电振子主要是为系统提供驱动力，致使系统发生共振，进而实现系统的输出功能[4]。目前压电振子的振动特性很多国内外学者进行了很多方面的相关研究。

对压电振子相关分析主要体现以下几个方面：利用有限元软件对固支和简支状态下压电振子进行了仿真分析，同时对压电振子动力学和静力学也进行了推导[5]；利用ANSYS软件对双晶片圆形压电振子和矩形压电振子进行模态分析，得到共振频率与结构尺寸参数关系，为压电振子的优化设计提供了理论依据[6]；利用板壳理论推导出了压电振子弯曲振动方程，并给出了增大压电振子振动位移的有效方法[7-8]。李东明等人对矩形压电振子的位移输出进行了分析，利用本构方程对矩形压电振子的振动位移进行了推导，得出了影响压电振子振动位移的表达式[9]。通过理论分析得出压电振子的固有频率与几何尺寸之间的关系，并与模态分析值对比，验证了理论分析的正确性[10-11]。

笔者通过弹性理论对圆形压电振子进行理论分析，推导出了压电振子的振动位移表达式，将圆形压电振子用于驱动共振隔膜泵，驱动效果较好。

1 机构组成与工作机理

圆形压电振子实物结构组成及振动形态如图1和图2所示。该圆形压电振子是将压电陶瓷片粘接在金属基板上，有单晶片和双晶片之分，单面陶瓷粘接为单晶片压电振子，双面粘接为双晶片压电振子。固定方式为周边固定支撑式，压电振子在交变信号的作用下往复振动，带动系统振动，这种刚度较大的振子一般是利用共振原理实现系统驱动。

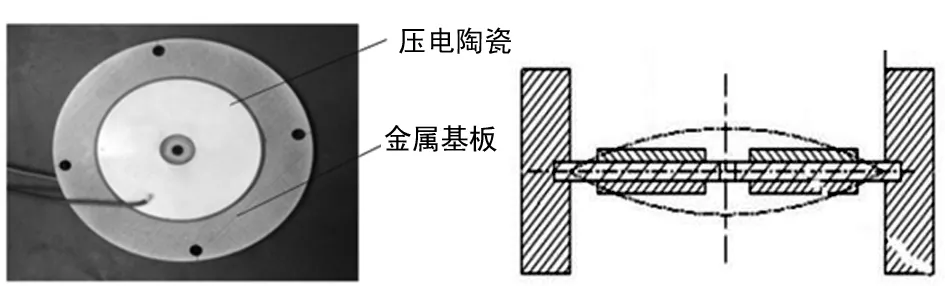
图1 压电振子结构组成 图2 压电振子振动形态

2 压电振子弹性分析

压电振子受力分析及尺寸如图3所示。金属基板的直径为d2,压电陶瓷直径为d1，弯矩为M2，激振力为T,弹性位移为W。

图3 压电振子受力示意图

金属基板边缘到压电陶瓷边缘(A-B)部分的挠度为：

(1)

式中：r为到压电振子中心的距离；D为的抗弯刚度。

压电陶瓷边缘到中心(B-C)部分的挠度为：

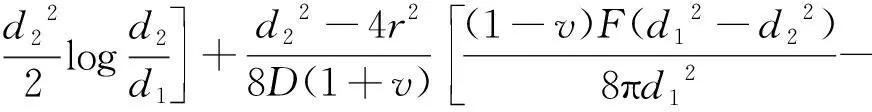
(2)

将外边缘挠度与弯矩M2迭加,得到板的挠度，边缘处的斜度为：

(3)

弯矩M2产生的斜度为：

(4)

令式(3)和(4)的和为0有：

(5)

此弯矩产生的挠度为：

(6)

通过式(5)、(6)，得出压电振子的挠度曲线。

其中(A-B)部分的挠度为：

(7)

(B-C)部分的挠度为：

(8)

由以上了理论分析可以看出，压电振子振动位移与驱动力、材料参数以及尺寸参数有关。

3 应用测试

3.1 实验装置

实验测试装置如图4所示，主要包括：隔膜泵系统样机、数字变频器、阻抗分析仪、激光测微仪、磁力支撑架、计算机、气体压力表，直流电源和流量计等仪器。激光测微仪主要用于测试系统振动位移，数字变频器提供系统驱动信号，阻抗分析仪主要用于测试系统共振频率及阻抗，气体流量计主要用于测试隔膜泵样机系统输出气体流量。

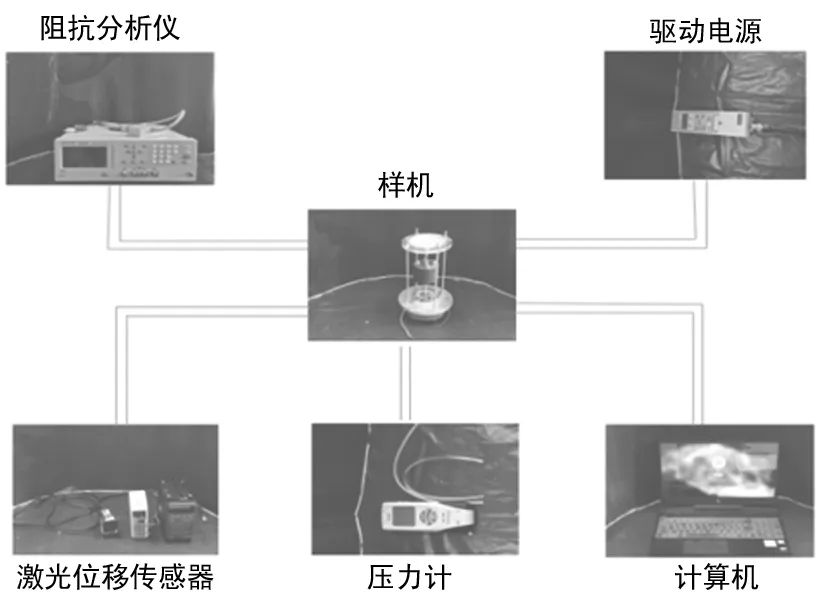
图4 实验测试装置

3.2 系统输出流量测试

将驱动电压调至200 V，改变变频器的驱动频率，得到隔膜泵输送气体流量随着驱动频率变化曲线值，测试结果曲线如图5所示。

图5 隔膜泵输出流量曲线图

从图中可以看出，系统输出流量随着驱动频率先增大后减小，当系统处在共振频率186.7时最大输出流量为986.8 mL将系统调至共振频率186.7 Hz，改变驱动信号的电压值，得到输出气体流量与驱动电压的关系如图6所示。

图6 隔膜泵输出流量曲线图

从上图可以看出，随着驱动电压的增大，隔膜泵输出气体的流量逐渐增大，基本呈线性关系。

3.3 隔膜气泵压力测试

实验测试过程中，将驱动电压设置为200 V，改变驱动频率，隔膜气泵的驱动压力曲线图如图7所示。

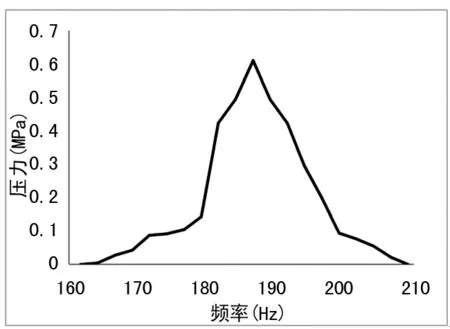
图7 隔膜泵输出压力曲线图

从图中可以看出，隔膜气泵输出压力随着驱动频率先增大后减小，当系统处在共振频率186.7时最大输出气体压力为0.6 MPa。

将系统调至共振频率186.7 Hz，改变驱动信号的电压值，得到输出压力与驱动电压的关系如图8所示。

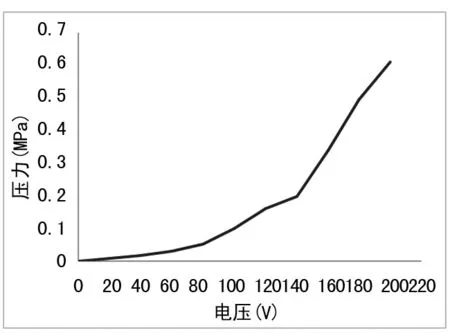
图8 隔膜泵输出压力曲线图

从上图可以看出，随着驱动电压的增大，隔膜泵输出气体的压力逐渐增大，基本呈线性关系。

4 结 语

对压电振子进行了理论分析与应用研究测试，利用弹性理论对压电振子的振动位移进行了推导。将其用于驱动微小型隔膜泵的驱动，压电振子能实现较好的系统驱动，性能良好。分析了系统输出流量与输出压力与驱动频率和驱动压电的关系。验证了用这种圆形压电振子实现微小型系统驱动是可行的、有效的。