全国名校必修5综合拔高卷（B卷）

■河南省南阳市二中 郭臣峰

一、选择题

1.已知数列{an}为等差数列，a2＝3，a5＝15，则a11＝（ ）。

A.39 B.38 C.35 D.33

11.当太阳光与水平面的倾斜角为60。时，一根长为2m的竹竿如图1所示放置，要使它的影子最长，则竹竿与地面所成的角为（ ）。

图1

A.30。 B.60。 C.45。 D.90。

12.在△ABC中，（a＋b＋c）（sinA＋sinB－sinC）＝asinB，其中a，b，c分别为△ABC三内角A，B，C的对边，则C＝（ ）。

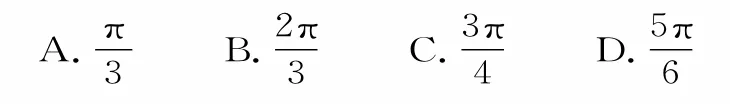
13.已知关于x的不等式ax2－2x＋3a＜0在（0，2]上有解，则实数a的取值范围是（ ）。

18.等比数列{an}的前n项和为Sn，若an＞0，q＞1，a3＋a5＝20，a2a6＝64，则S5＝（ ）。

A.48 B.36 C.42 D.31

19.设z＝－x＋2y，其中x，y满足

A.21 B.22 C.23 D.24

20.已知实数a＞0，b＞0，且＝1，则a＋2b的最小值是（ ）。

21.我国南宋著名数学家秦九韶提出了由三角形三边求三角形面积的“三斜求积”，设△ABC的三个内角A，B，C所对的边分别为a，b，c，面积为S，则“三斜求积”公式为S＝。若a2sinC＝5sinA，（a＋c）2＝16＋b2，则用“三斜求积”公式求得△ABC的面积为（ ）。

22.已知数列{an}为等比数列，an＞0，且amam＋1am＋2＝26m，若p＋q＝6，则ap·aq＝（ ）。

A.27B.28C.29D.210

23.已知函数f（x）＝ax＋2a－1的图像恒过定点A，若点A在直线mx＋ny＋1＝0上，其中m·n＞0，则的最小值为（ ）。

A.136 B.120 C.68 D.40

27.在△ABC中，已知角A，B，C的对边分别为a，b，c，若a＝n＋1，b＝n，c＝n－1，n∈N*，且A＝2C，则△ABC的最小角的余弦值为（ ）。

28.设△ABC的三个内角A，B，C成等差数列，sinA，sinB，sinC成等比数列，则这个三角形的形状是（ ）。

A.直角三角形 B.等边三角形

C.等腰直角三角形 D.钝角三角形

29.已知当x∈（0，＋∞）时，不等式9xm·3x＋m＋1＞0恒成立，则m的取值范围是（ ）。

35.音乐中使用的乐音在高度上不是随意定的，它们是按照严格的数学方法确定的。我国明代数学家、音乐理论家朱载堉创立的十二平均律是第一个利用数学使音律公式化的人。十二平均律的方法是精确规定八度的比例，把八度分成13 个半音，使相邻两个半音之间的频率比是常数，如表1 所示，其中a1，a2，…，a13表示这些半音的频率，它们满足log212＝1（i＝1，2，…，12）。若某一半音与D#的频率之比为，则该半音为（ ）。

表1

A.F#B.GC.G#D.A

36.已知数列{an}的前n项和为Sn，且3Sn＝4an＋3n。若函数f（x）是定义在R 上的奇函数，且f＝f（x），f（3）＝2，则f（a4）＋f（a5）＝（ ）。

A.－2 B.0 C.2 D.4

A.2019 B.2020

C.2021 D.2022

二、填空题

41.已知等差数列{an}的前n项和为Sn，且a8－a5＝－6，S9－S4＝75，则Sn取得最大值时n＝_____。

42.在△ABC中，角A，B，C所对的边分别为a，b，c，如果2b＝a＋c，B＝30°，△ABC的面积为，那么b＝____。

43.在等差数列{an}中，an＞0，且a1＋a2＋a3＋…＋a10＝30，则a5a6的最大值是______。

47.海伦是古希腊亚历山大时期的数学家，以他的名字命名的“海伦公式”是几何学中的著名公式，它给出了利用三角形的三边长计算其面积的公式S△ABC＝，其中p＝。若△ABC中，a＝5，b＝6，c＝7，则借助“海伦公式”可求得△ABC的内切圆半径r的值是____。

48.已知x＞0，y＞0，且＝2，若2x＋y≥m2－恒成立，则实数m的取值范围为____。

三、解答题

61.已知等比数列{an}中，a1＝1，且a2是a1和a3－1的等差中项。

（1）求数列{an}的通项公式；

（2）若数列{bn}满足bn＝2n＋an（n∈N*），求数列{bn}的前n项和Sn。

62.已知函数f（x）＝－x2＋a（5－a）x＋c。

（1）若c＝16，解关于a的不等式f（2）＞0；

（2）若a＝4，对任意的x∈（－∞，1]，f（x）＜0恒成立，求实数c的取值范围。

63.在△ABC中，角A，B，C所对的边分别是a，b，c，且btanA＝（2c－b）tanB。

（1）求A的大小；

（2）若a＝2，且△ABC的面积为，求b＋c的值。

64.设函数f（x）＝mx2－mx－2。

（1）若对于一切实数f（x）＜0 恒成立，求m的取值范围；

（2）若对于x∈[1，3]，f（x）＞－m＋2（x－1）恒成立，求m的取值范围。

65.设等差数列{an}的前n项和为Sn，且S4＝4S2，a2＝2a1＋1。

（1）求数列{an}的通项公式；

（2）设数列{bn}满足bn＝，求数列{bn}的前n项和Rn。

66.如图2，某市欲建一个圆形的公园，规划设立A，B，C，D四个出入口（在圆周上），并以直路顺次连通，其中A，B，C的位置已确定，且AB＝2，BC＝6，记∠ABC＝θ，且已知圆的内接四边形对角互补。请你为规划部门解决以下问题：

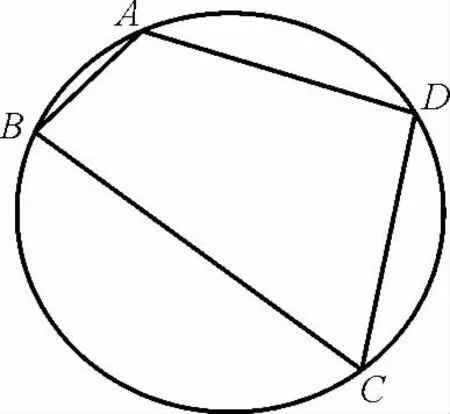
图2

（1）如果DC＝DA＝4，求四边形ABCD的区域面积；

67.已知在△ABC中，∠ACB＝，角A，B，C的对边分别为a，b，c。

（1）若a，b，c依次成等差数列，且公差为2，求c的值；

（2）若△ABC的外接圆面积为π，求△ABC周长l的最大值。

68.已知数列{an}中，a1＝1，a2＝3，其前n项和为Sn，且数列{Sn}为等比数列。

（1）求数列{an}的通项公式。

（2）若bn＝，记数列{bn}的前n项和为Tn。设λ是整数，问是否存在正整数n，使等式成立。若存在，求出n和相应的λ值；若不存在，请说明理由。

69.已知函数f（x）＝mx2＋2nx＋1。

（1）若不等式f（x）≤0的解集为[1，2]，求m，n；

（2）设A＝{x｜f（x）≥0}，且－1∈A，2∉A，求m＋3n的取值范围。

70.已知数列{an}中，a1＝a2＝1，且当n≥2，n∈N*时满足nan＋1＝（n＋1）an。

（1）求数列{an}的通项公式；

（2）设bn＝2n，若对任意的n∈N*，数列{bn}是单调递减数列，求实数λ的取值范围。