大范围三维地形动态可视化技术研究

董兴鹏 陈伟 张丽 郑雄伟 黄炜

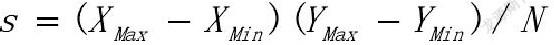
摘要：三维地形以数字化的方式对地形表面起伏状态和细节特征进行模拟，广泛应用于飞行视景仿真、战场态势仿真、模拟演练、应急指挥、灾害救援等应用场景中。三维地形的真实性和可视化渲染的实时性直接决定了三维应用场景的逼真度、沉浸感和有效性。文主要针对地质遥感数据成果可视化及共享展示，解决地质遥感数据体三维展示效果不佳，地质调查成果数据展示组织方式欠缺，可视化系统性能欠佳的问题，提供了优化的数据存储渲染技术、多维一体化地质大数据成果组织方式、综合可视化承载平台以及数据关联分析功能，为地质调查应用系统中的遥感地质可视化分系统提供技术模块。

关键词：三维展示，关联分析，模拟演练

Abstract：3D terrain is used to simulate the undulating state and detailed features of terrain surface in a digital way，which is widely used in flight scene simulation，battlefield situation simulation，simulation exercise，emergency command，disaster rescue and other application scenarios. The reality of 3D terrain and the real-time of visual rendering directly determine the fidelity，immersion and effectiveness of 3D application scene. This paper mainly aims at the visualization and sharing display of geological remote sensing data，solves the problems of poor 3D display effect of geological remote sensing data volume，lack of organization mode of geological survey data display，and poor performance of visualization system，and provides optimized data storage and rendering technology，multi-dimensional integrated geological big data achievement organization mode，comprehensive visualization bearing platform and data Customs Combined analysis function provides technical modules for remote sensing geological visualization subsystem in geological survey application system.

Key Words：3D display;association analysis;Simulated drill

1前言

地球表面是人類社会赖以生存并从事一切实践活动的根基，人类的生产生活与其发生着紧密的联系（刘学，2011），地形与地貌是表达地表的最重要自然地理要素。地理学、测绘学和地貌学等学科中一直把对地形的科学表达作为研究重点和热点，随着计算机图形学的发展，将物理世界的三维特征用计算机进行真实的再现已成为现实（朱永丽，2012），三维地形构建技术应运而生。基于高精度和高分辨率的地形空间渲染、更细腻的地表细节呈现、更绚丽的地上景观模拟、更丰富的光照渲染效果、更便捷流畅的交互操作成为虚拟现实三维场景普遍需求（郭浩然，2013），然而这些需求又反向推动地形三维重建的发展。目前，三维地形重建以及基于地形的可视化应用面临挑战。大范围三维地形场景的真实感表达与呈现为三维场景可视化应用处理的实时性带来挑战。在大规模的虚拟现实三维应用场景中，准确的绘制地形的起伏特征、逼真的渲染出地表要素都与场景的实时快速渲染相互矛盾，寻求既能满足大规模地形渲染真实感的要求又能满足实时可视化需求的方法，值得深入研究。

2基于Delaunay准则和生长法的网格化方法

在分析了三维空间离散点云网格化方法的基础上，结合无人机序列图像生成地面点云数据的特点，本文采用生长法依据 Delaunay准则对获取的地面点云数据进行网格化。

2.1构建可伸缩包围盒

地形点云数据与其他点云数据相比，具有数据量大、不封闭、空间范围广的特点，采用传统等大小包围盒的剖分方法对地形点云数据进行剖分会产生许多空包围盒，造成空间的浪费和搜索效率的下降。同时，考虑到地形点云数据的高程特性和连续性，点云在水平面上投影邻近的点在空间中也是邻近的，所以本文提出沿地形高程方向可伸缩的包围盒对地形点云数据进行空间剖分。

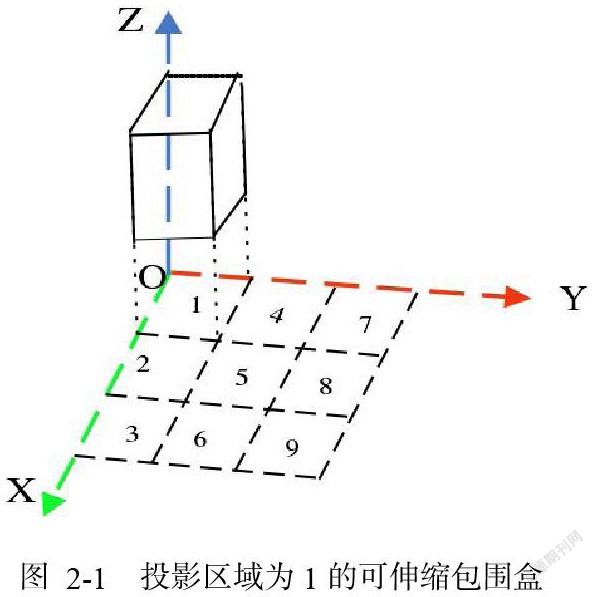
可伸缩的包围盒是一种长方体包围盒，该包围盒垂直于高程方向的一组面的大小固定，而沿着高程方向的长度可以自由伸缩，以便包围所有投影在该组平面内的点。假设xoy为水平面，z轴为地形的高程方向，图2-1投影区域为1的可伸缩包围盒，包围盒固定大小的一组面与xoy 平面平行，其沿z轴方向的长度不固定。此时整个空间剖分的包围盒个数只与点云数据所在平面投影区域面积的大小成正比，极大地减少了包围盒的数量。

为了确定点云在xoy投影区域的大小，在读入点云数据的同时，记录下点云的x、y坐标的最大值和最小值 Xmax、Xmin、Ymax、Ymin。

为了确定小正方形的边长，需要计算平均每个投影点的投影面积s，s按照下方公式计算，其中N为点云中点的总数量。

每个小正方形的边长e按照公式计算，m为平均每个正方形内的投影点个数，m为整数（本文中m=5），s为公式的结果。

2.2计算空间邻近点

可伸缩包围盒的构建极大地缩小了一个点的空间邻近点的范围。如图2-2xoy投影平面的剖分图所示，包围盒6中点的空间邻近点一定在包围盒6和与其相邻的8个包围盒共同组成的空间中。若采用空间点邻近的全部包围盒中的点来定义该点的空间邻近点范围时，当空间点位于自身所在包围盒的边缘时，存在较大的误差无法准确的描述其邻近点。本文在包围盒的基础上通过与可变半径的包围球求交运算来确定空间邻近点。若要求任意一空间点P的邻近点，定义V为其邻近点的集合，初始为空，首先计算点P自身包围盒编号Pnum以及邻近的8各包围盒编号，然后构造球心为P的包围球Q，将所有包围盒与包围球Q求交，将获得的点加入到集合V中，如为空则增大包围球的半径，直至V非空或包围球半径大于给定阈值为止。

2.3种子三角形的确定

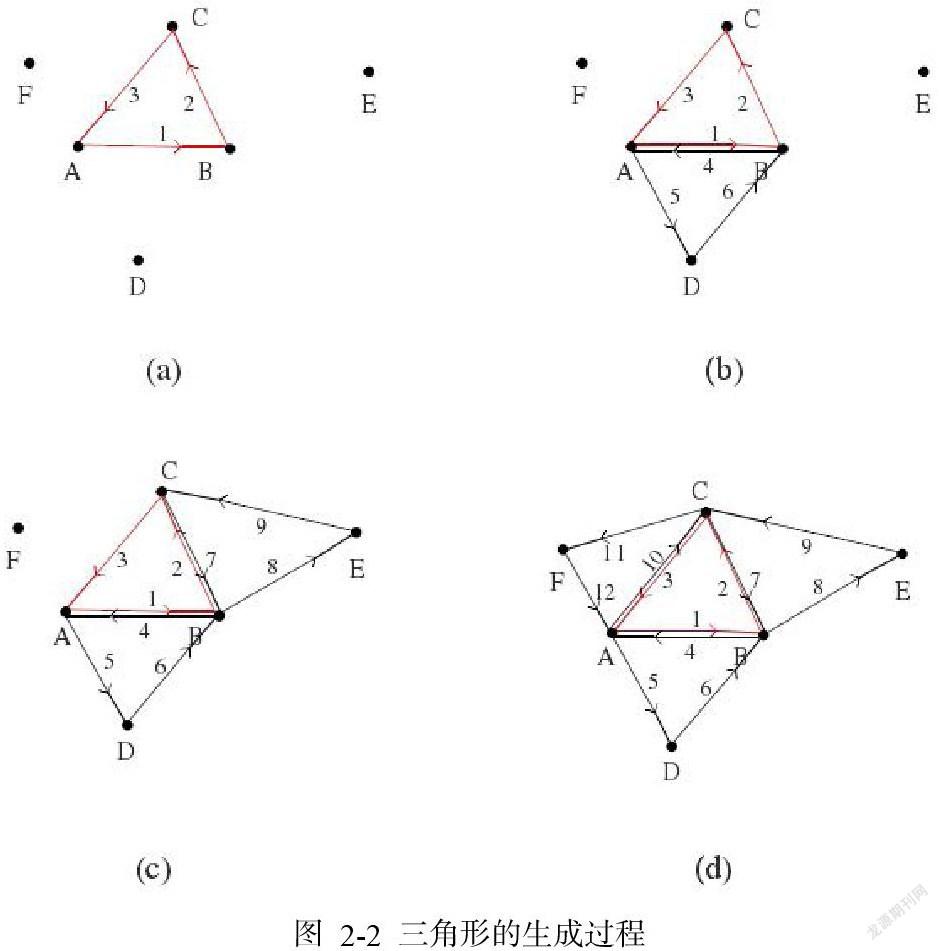
本文基于生长法生成地形网格，首先需要选取三个顶点构成一个种子三角形，然后依据生长算法进行网格的生成。同时为了后续网格绘制和显示的需要，网格生成时按照右手法则给出生成三角面的正面，即三角形中各顶点的顺序由右手法则确定（陈思环，2018）。图2-2是对投影平面上的6个点A、B、C、D、E、F的三角网格化示意过程，其中△ABC 是种子三角形如图2-2 a所示，依据右手法则确定种子三角形顶点的顺序为 A->B->C，从而确定了种子三角形的正面;然后按照△ABC 边的生成顺序进行搜索最邻近点，依次生成△BAD、△CBE 和△CAF。三角形的生成过程如图：

种子三角形顶点的确定：本文中基于生长法的点云三角网网格化过程中三角形的生成是采用广度优先算法来对种子三角的边进行扩展生成新三角形。种子三角形的确定对点云网格化结果影响较小，所以种子三角形可以依据实际需要指定其初始位置。本文在进行种子三角形的第一点选择时，选取所有点云中坐标最小点作为第一个点，依据图中空间邻近点的计算算法，求出p1的邻近点集合v1，在集合v1中取出最近邻点p2，计算出p2的邻近点集合v2，求集合v1和集合v2的交集v3，在求出距离上面两个点距离和最小的点p3，同时要求点p3与p1、p2生成的三角形为锐角三角形，该三角形即为种子三角形。

种子三角形方向的确定：在对点云网格进行渲染时，需要确定网格三角形的正面，剔除网格的背面来加快网格化渲染的速度。为了保证生成的网格中所有三角形的正面是目标区域地形表面，本文采用右手法则给出生成三角面的正面，即三角形中各顶点的顺序由右手法则确定。在所生成的三角网格中相邻的两个三角形（有2个共同的顶点）的公共边方向相反，在种子三角形方向已知时，后续扩展的三角形顶点顺序按照传递性来获取。所以在地形网格生成时，为了保证生成的网格的方向同地形的外表面一致，只需要使得初始的种子三角形p1p2p3的正面与地形的外表面一致即可。

地形有三种类型的地势，平地、低谷和山峰，如图2-3地形截面图，图中粗线以上部分是地形外表面，以下是地形内表面。若地形外表面使用逆时针方向，则外法线方向与空间坐标系中的Z轴所形成的夹角小于 90°，因此通过夹角来判断生成三角形顶点的顺序。以种子三角形为例若cosβ ≥ 0时，三角形的顶点顺序是p1p2p3，反之三角形的顶点顺序是p1p3p2。

2.4广度优先搜索过程

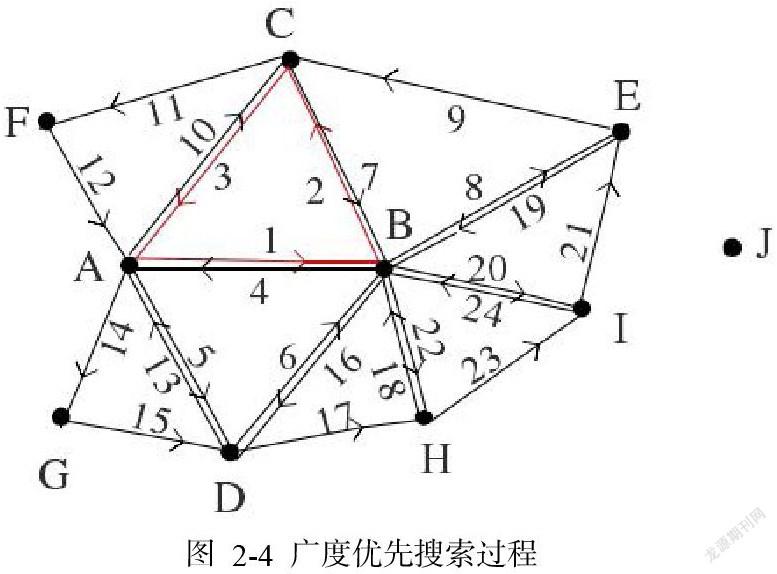
在确定了种子三角形后，需要按照生长法来扩展生成新三角形，最终完成网格的构建，在新三角形生成过程中采用广度优先的搜索算法来对种子三角的边进行新三角形的扩展。为了便于对三角形生成过程的描述，对网格生成过程中（图2-4）的点和边进行如下定义：内边：邻接三角形的公共边。如边AB（BA）、BC（CB）、AC（CA）、AD（DA）、BD（DB）、BH（HB）、BI（IB）、BE（EB）。

外边：未生成邻接三角形的边。如边AG、GD、DH、HI、IE、EC、CF、FA。

内点：以其为顶点的边都是内边的点称为内点。如点B。

外点：以其为顶点的边中含有外边的点称为外点。如点A、G、D、H、I、E、C、F。

待连接点：不是任何三角形的顶点的点称为待连接点。如点 J。

图中种子三角形是△ABC，当种子三角形选定后，依据右手法则确定种子三角形的正面，即种子三角形顶点的顺序，按照种子三角形的顶点顺序依次生成种子三角形的三条边。在种子三角形的基础上，依照广度优先的搜索策略从外边中选择一条边进行新三角形的扩展。如图 2-4中种子三角形的外边生成顺序是AB->BC->CA，在进行新三角形扩展时，首先选择外边 AB 作为新三角形的一条边，查找构成新三角形的另一顶点 D，生成外边 AB 的邻接三角形BAD，同时AB变为内边。新生成的△BAD 的边AD和DB成为了外边。这时生成的网格中的外边有 BC、CA、AD 和 DB，按照广度优先的搜索策略，外边按照 BC->CA ->AD->DB的顺序扩展新的邻接三角形，分别是：△CBE、△ACF、△DAG、△BDH。

2.5最优点的候选点集确定

基于生长法进行点云数据网格化构建的过程是一个不停的为已知的外边选择第三个顶点生成新三角形的过程，第三点的搜索集合称为外边的候选点集。在保证网格构建效果的前提条件下，为了加快网格的构建，应尽可能的缩小第三点的搜索范围即缩小候选点集，因此对第三点做如下限制来缩小候选点集。假设当前需要進行三角形扩展的外边是 MN，V 是外边 MN 的候选点集，V 内的点需满足如下要求：

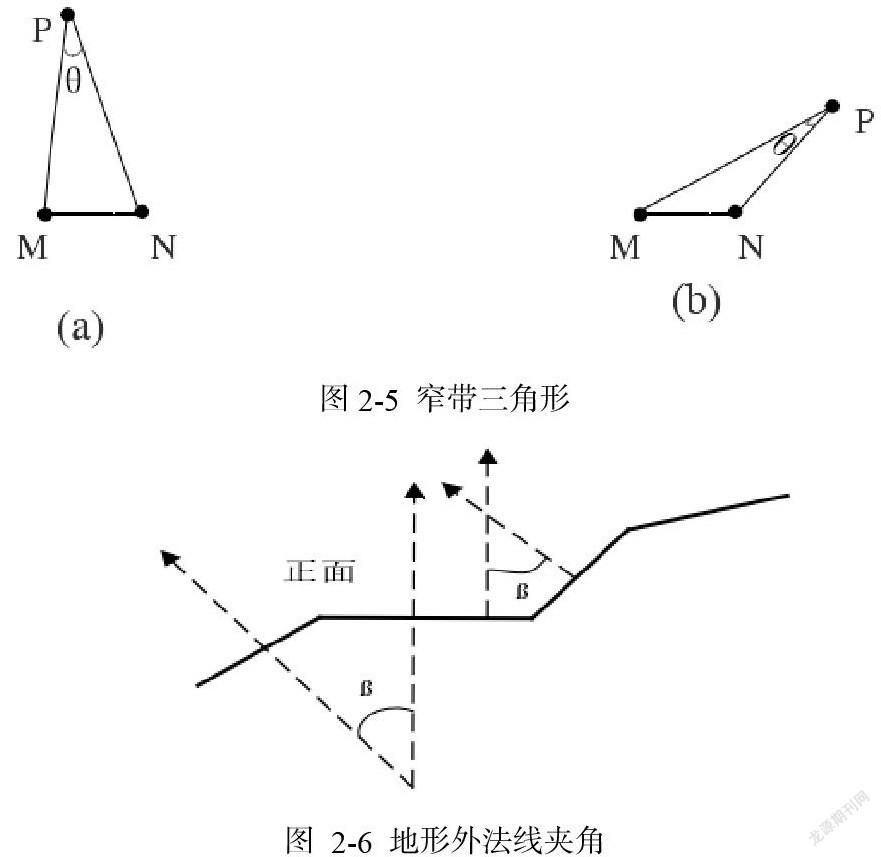
⑴最大化最小角特性限制。三角形中最小角最大，即相邻两三角形组成的凸四边形互换对角线，六个内角中的最小角没有增大。为了使新扩展的三角形形态更优，防止生成窄带三角形（如图 2-5），新生成的三角形中最小内角不小于一个下限阈值，在本文中的值为π6。

⑵二面角限制。为使重建的地形表面连续且平滑，假设外边MN所在的三角形为△MQN，顶点P与外边 MN 生成的新三角形为△MNP，△MQN 与△MNP之间的二面角越接近π2越好。在网格构建时已经对三角形的正面进行了一致化，为了保证生成的网格的方向同地形的外表面相同，即网格中全部三角形对应的法线方向都由内表面指向外表面。因此，可以通过限制△MQN和△MNP法线的夹角来实现△MQN与△MNP之间的二面角的限制，夹角越小，两个三角形的二面角就越趋近π2，如图2-6。

通过夹角来判断两邻接三角形的平滑性，以边 MN 的两个邻接三角形为例，本文要求的余弦值需要满cosβ>0，即的最大上限阈值为2。

⑶非法点限制。第三个顶点P不能是已生成网格的内点、点P不能是已有三角形 MQN 的顶点、点P不與MN共线。

⑷边限制。边MP与NP不为内边。

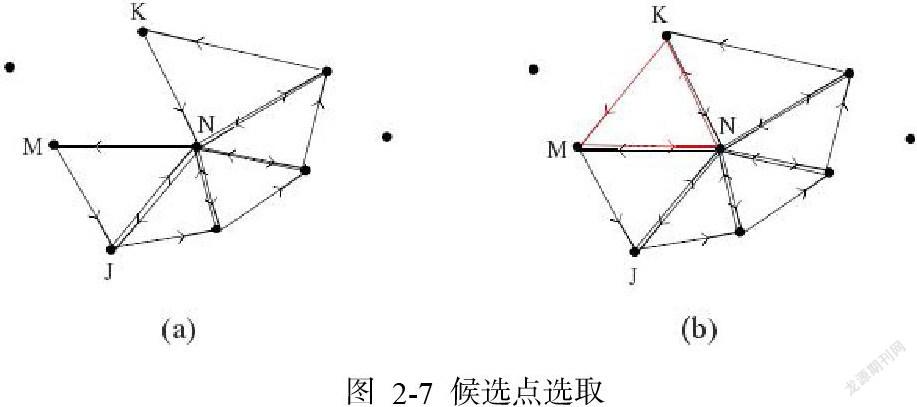
以外边 MN 为例，其候选点集合V可采用如下算法进行确定：第一步：在外边MN两个顶点的邻接外边的顶点中进行检索，尽快完成外边MN的三角拓展;若检索到的邻接点满足上述（1）、（2）、（3）、（4）限制条件，判定该点为候选点加入V中，若集合V为空转入下一步，反之结束搜索，图 2-7表示了该步骤的搜索过程，从图2-7a中可知确定点J和点K为符合条件的顶点，由于顶点J是已有三角形的点判定为非法点，点K为满足条件的候选点，与外边MN生成新三角形MNK。

第二步：对两个顶点 M、N 所在包围盒内的其他点进行判断，若满足上述（1）、（2）、（3）、（4）限制条件，判定该点为候选点加入 V 中，待所有点判断完成后，若集合V为空转入下一步，反之结束搜索。

第三步：按照邻近点计算方法，分别求外边顶点M、N的邻近点以M、N为圆心，初始半径r=e时的邻近点集（不包括已经搜索过的点），对检索到的所有点进行判断，若满足（1）、（2）、（3）、（4）的限制条件，判定该点为候选点加入V中，待所有点判断完成后，若集合V为空增大邻域半径r，扩大搜索范围，继续第三步，直至V非空或r达到阈值R。

阈值R是针对在地形边缘网格生成时给定的限定条件，避免无意义的查找。半径r增大的步距和上限阈值R可通过实验获得，在本文中依据本章后续实验，设r的步距e，R=2e。上述搜索过程结束时，若候选点集V为空，则将MN记为边界边;若候选点集V中只有一个唯一点，则该点就是MN构成新三角形的最优点;若候选点集V中存在多个候选点，需要对点集中的候选点进行量化评价，选出最优点做作为生成新三角形的最优候选点。

2.6候选点的评价函数

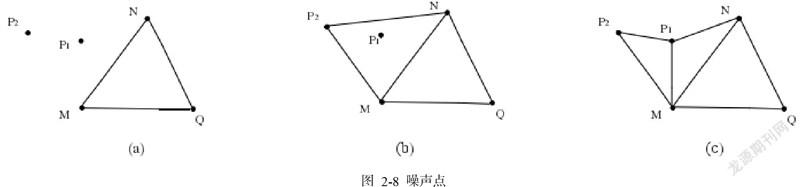
通过上节的算法可以求出外边 MN 的候选点集 V，当候选点集 V 中含有多个候选点时，需要定义一个评价函数对集合 V 中的点进行量化评价，依据评价结果确定最优点做作为生成新三角形的最优候选点。多数评价函数从新生成的三角形是否接近 Delaunay 三角形和地形网格的平滑度方面去考虑，而忽略了候选点到外边的距离对整个网格的影响。图 2-8 a 中 MN 是外边，点 P1和点 P2是外边 MN 候选点集合中的两个候选点，点 P2与外边 MN 生成的三角形△MNP2与其邻接的△MQN 形成的二面角更接近 180°。△MNP2的最小内角比△MNP1大。

若仅考虑地形平滑度和 Delaunay 特性的限制，点 P2是生成新三角形的最优点，生成的新三角形图

图2-8 b所示，而点 P1由于不满足相邻三角形的二面角的限制，不能与其他任何外边形成三角形而成为噪声点。若果选择候选点P1进行新三角形的生成，可生成△MNP1同时点P2在后续网格化中可生成△MP1P2，如图 2-8 c 所示，此时点P1和P2都是有用点。出现图2-8 b这一现象的原因是候选点P1与外边MN的距离更近，且候选点P1在平面MNP2上的投影点在△MNP2内部，显然 MP1 NP1 MP2NP2 。在网格构建时为了避免类似情况的发生，在最优候选点选择时，应综合考虑地形平滑度、Delaunay 三角形最小内角和候选点到外边的距离。

3.总结

三维地形以数字化的方式对地形表面起伏状态和细节特征进行模拟，广泛应用于飞行视景仿真、战场态势仿真、模拟演练、应急指挥、灾害救援等应用场景中。以无人机采集的序列图像进行三维地形重建相比传统方式进行大范围三维重建在成本、效率、数据现势性等方面都具有巨大优势。本文围绕着基于无人机采集到的序列图像进行大规模地形三维重建的关键技术展开研究，分别从序列图像的特征提取、图像匹配、稀疏重建、稠密重建、离散点云网格化、地形数据可视化、大规模地形实时渲染等多个方面展开，对重建过程中的关键问题予以解决，给出了具体的解决办法，概括起来本文的创新性工作体现在以下方面：

针对离散点云数据的三维重建网格化方法进行研究，结合无人机序列图像获取到的地形点云数据的特点，提出了一种基于 Delaunay 准则和生长法的网格化方法来完成离散地形点云数据的快速网格化方法。该方法首先采用可伸缩包围盒对空间进行剖分，求点的空间邻近点（k-邻近点）;然后从点云中选取一个带方向的种子三角形，并设计点和边的搜索策略;最后以已有的外边为基础，确定外边的候选点集，并从该外边的候选点集中选择一个最优点，增量式地生成新的三角形。

参考文献

[1]白春红.基于领域本体的语义图像检索研究[D] .重庆大学，2012.

[2]常方媛.基于无人机航拍图像的三维地形重建[D].天津大学，2014.

[3]陈姣，米鸿燕，李超，等.基于无人机遥感系统应用与影像有效利用的探讨[J].价值工程. 2013：181-183.

[4]陈蔓，钟勇，李振东. 基于SIFT字典学习的引导滤波多聚焦图像融合[J]. 哈尔滨工业大学学报，2018，50（11）：65-72.

[5]陈思环.基于散乱点云数据的表面重建关键技术研究[D].中国科学院大学.2018.

[6] 陈庭旺，王庆.面向大规模场景的三维线段检测算法[J].计算机辅助设计与图形学学报，2011，23（5）：790-796.

[7]郭向坤.大规模三维地形构建的关键技术研究.中国科学院沈阳计算技术研究所.2019

作者简介：董兴鹏（1986- ），男，汉族，本科，研究方向：计算机应用。

陈伟（1979- ），男，硕士，研究方向：人工智能与大数据应用。

基金项目：本文受高分辨率对地观测系统重大专项（GFZX0404130302）项目资助。