寻其芳踪去有“圆”自然成

秦威

摘  要：图形运动中的几何问题，有着独特的数学魅力. 同时，这类问题的探究对学生的观察能力、想象能力和分析问题能力有着很高的要求，学生往往望而生畏. 以作辅助圆解决运动图形中最值问题为题材的拓展教学，有助于学生对此类问题的深入理解. 文章通过对三类问题的剖析，挖掘问题本质，追溯知识源点，构建解决这类问题的一般思路，使学生积累解题经验，提升数学素养.

关键词：图形运动;最值问题;圆

在几何解题教学中，线段最值问题是一个难点，学生常常对此类问题感到困惑. 本文突出作辅助圆解决一类线段最值问题的拓展教学引导，揭示图形运动变化的特征，发展学生的直观想象能力，探寻解题思路来源，引导学生积累解题经验，提升数学素养.

一、铺设问题引导，解法自然生成

解题是激活已有解题经验，并积累新的解题经验的过程. 在几何动点问题的解题教学中，依据学生已有的数学知识和解题经验，寻求动点的运动特征，有利于发散学生的想象思维和推理判断能力. 教师通过铺设有层次的问题引导，可以让自然解法破土而出.

1. 定点、定长随圆动

将一个复杂且陌生的问题变为简单且熟悉的问题，把问题从一个高度递减式分解成若干个符合学生“数学现实”的问题是一种有效的解题策略. 对于此题，教师可以对学生做以下引导.

（1）题目中，哪些点是动点，哪些点是定点？

（2）连接GD. GD的长度在[EF]取不同位置時，发生变化吗？点G做怎样的运动？

（3）如果点G是固定的，如何求PA+PG的最小值？

（4）如果点P是固定的，如何求PG+GD的最小值？

问题（1）引导学生将题意和图形相融合，意在让学生理清题意. 问题（2）是解决问题的关键点，通过引导让学生发现GD的长度不变. 提出这两个问题的目的在于引导学生从图形的运动中，把握不变的因素，根据这些不变的量，确定点G的运动形式，发现问题的本质. 提出问题（3）（4）的目的是引导学生回溯已经具备的解题经验. 如图5，以点D为圆心、DG为半径的作⊙D，延长AB至点A，使AB=AB，连接AP，AD.通过回顾“将军饮马”模型和“圆外一点到圆上一点的最短距离”问题的解题思路，让此题的解题方法渐渐显露. 在这样的引导下，学生的思考经历了“拨云见日”的过程，思维的指向更加明晰.

在求解数学问题的过程中，把有难度的问题转化成若干个阶梯式小问题，有助于学生思维向更高一级层次发展. 例1中通过折叠产生了定长MA，例2在直角三角形中产生了定长DG. 通过问题引导，有助于学生抓住这些不变的量，根据“到定点的距离等于定长的点在同一个圆上”添加辅助圆，找出相应点的运动特征，转化问题，破解难点.

2. 定角、动弦暗生圆

例3  如图6，在矩形ABCD中，AB=3，BC=3，动点E，F分别在AC，BC上，且∠ABE=∠BFE， 则BF的最小值为 ____  .

根据题目中的信息可以发现条件∠ABE=∠BFE是解题的关键点，挖掘这一关系中隐含的信息，有助于突破难点. 因此，教师可以对学生进行如下引导.

通过以上问题的引导，学生的解题思路将拾级而上. 然而，在问题（4）上，学生容易出错，直接认为当[OE⊥AC]时，OE取最小值，这样的思路是有缺陷的. 问题（4）的给出在于突出易错点，引发后续思考. 因此，教师需要指出，若点O是定点，那么当[OE⊥AC]时，OE取最小值，则BF也取最小值. 但是在此题中，随着点E的运动，点F也是运动的，从而点O也是运动的，所以不能直接说当[OE⊥AC]时，OE取最小值. 此题的具体解法如下.

例4  如图9，点A是直线y=-x上的一个动点，点[B]是x轴上的动点，若AB=2，则△AOB面积的最大值为_____ .

此题在定角和动弦的对应关系下，添加辅助圆，通过问题的引导，将问题的本质挖掘显现，从面积问题转化为求三角形高的问题，再从三角形的高与所隐含的动圆之间的关系，去发现高取最大值时的状态. 这样把一个复杂的问题引向了学生具备的“数学现实”，使得学生在思考中收获了对知识本质的理解.

解决此类问题时，抓住不变的元素是关键，构建辅助圆，再根据条件寻找与已有知识之间的联系. 不难发现，运动中存在角度不变的情况，可能与所学过的圆周角有联系，通过知识筛选，得出问题中的角在某一圆周上，从而使思维进一步向问题指向靠近.

3. 动角、定弦圆犹在

二、唤醒解题思路，展现思维流程

1. 问题引导，关注思维流线

上述的问题引导，立足于思考教学生如何想，从哪里着手解题，通过具有层次性问题的引导，让学生拾级而上，最终获得解题思路. 有助于学生思维的发展和解题经验的积累. 在例1中，设置了5个问题，从题目的条件出发，探索翻折过程中不变的量，引发学生对这些不变量之间关系的本质思考，寻求点[A′]的运动特征，在分析的过程中形成有序的思考. 例2的引导是把问题转化成若干个阶梯式的小问题，通过问题的层层推进，使得学生的思维向更高一级层次发展. 这些问题的引导，使得学生的思维流线更加自然.

2. 问题类比，积累解题经验

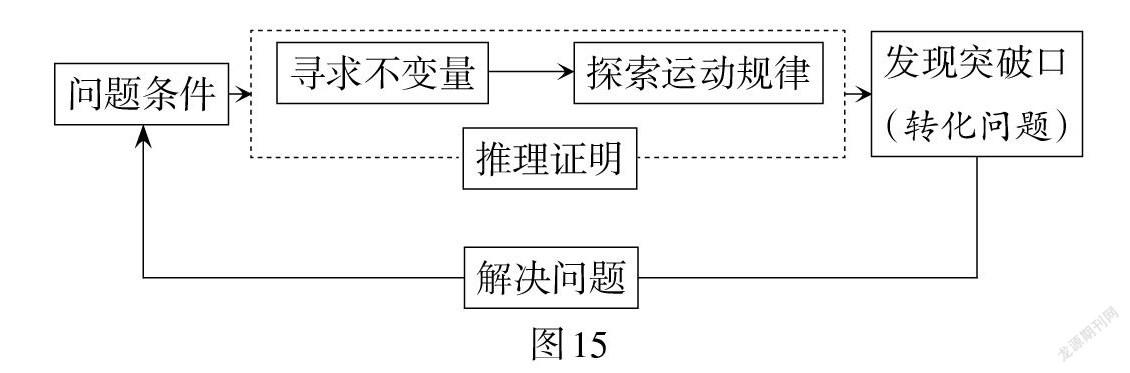
在几何解题教学中，注重数学思想方法的归纳和总结，通过问题的类比，可以让学生对知识的理解更加通透. 例6相对于例5更加复杂，因为学生对“90°的圆周角所对的弦是直径”的理解更为明晰，在例6中，弦AB所对的圆周角为120°，从而得出点P的运动特征，突破问题求解的思维障碍. 对“定点、定长”“定角、动弦”“动角、定弦”三类问题分别展现两道例题求解的思维过程，有助于学生掌握不同类型问题的分析方法. 在理解知识的基础上，探寻运动图形中的不变元素，发现动点的运动规律，进而通过知识类比，实现数学推理，在这样的引导过程中，形成一类问题的解法（如图15）.

3. 抓住本质，提升核心素养

上述6道例题，分别从不同角度引导学生进行思考，通过添加辅助圆实现问题的解决. 将这一内容作为拓展教学，通过条件分析，挖掘运动中不变的元素，探寻知识之间的关联，把新问题转化为熟悉的问题，进而实现问题的求解. 在解题过程中，教师设置引导式问题，有助于学生发现这类问题思考的切入点，提升数学思维品质.

参考文献：

[1]钱宜锋. 一道填空压轴题解答切入点的探究[J].中学数学教学参考（中旬），2019（4）：51-53.