彰显习题设计取向 提升数学作业价值
2021-12-02赖婉秋
赖婉秋

如何设计有吸引力、有学科特性的作业,让学生在完成作业的过程中感受知识的价值,是广大教师努力的目标。笔者认为,作业设计应以学生核心素养的发展为着力点,以促进学生对知识的掌握为基础,不断创新作业的形式,提升作业实效。
一、突出生活性,注重学有所用
数学源于生活,又用于生活。教师要摒弃那些单调的、重复性的数学习题,选取一些与学生生活实际接轨、富有童趣的生活素材来设计学生作业。这样不仅能激发学生的学习兴趣,促进他们顺利完成作业,达到巩固知识的目的,还有利于培养学生的知识应用意识。
例如,这样两道题:(1)2020年6月21日下午,我国出现了日环食天文奇观。小明观测到日环食从14:44初亏,17:24复圆。小明观测到的日环食经过的时间是多长?
(2)“眼睛离书一尺远,手离笔尖要一寸,胸离桌沿要一拳。”这是写字时要注意的三个一。这里的“一尺”就是眼睛离书本的距离约( )比较合适。
A. 33毫米 C. 33分米 D. 33米
如上两题,把天文现象、卫生口诀中体现的数学知识有机地融入到习题中,不仅让学生体验到数学与生活的紧密联系,充满乐趣的题目也让学生在完成的过程感受数学的博大。
二、体现过程性,提升思维水平
数学教学不是简单地让学生把一些数学公式、推理结果记下来,而是要引导学生参与知识的探究过程。在作业环节,教师可以将延伸性知识巧妙地融入习题中,让学生在解决问题的过程中,不知不觉地参与知识的探究过程,从而让学生更加深入地把握知识的本质,提升数学思维水平。
例如,在教学“长方形和正方形的周长”后,笔者设计了如下习题:用24个边长都是1分米的正方形拼出长方形或正方形,有多少种不同的拼法?请画图表示各种拼法。各种拼成的图形的周长是多少?你可以发现什么数学规律?
学生发现把24个正方形拼成一排,长是24分米,宽是1分米,周长是50分米;拼成两排,每排12个,长是12分米,宽是2分米,周长是28分米……随着排数增加,拼成的长方形的长不断地变短、宽不断地变长,长和宽的差越小,周长也越来越短,所拼成的图形越来越接近正方形。
这样的习题暗藏数学规律,学生不仅仅是解决拼成的长方形或正方形的周长,更重要的是在多种拼法和与之相对应的周长计算中,发现了所拼长方形的长和宽的长度差距越小,也就是越接近正方形时,图形的周长就越短的数学规律。整个探究过程巧妙地融于作业中,学生既巩固了课堂知识,也发现了新知。
三、指向典型性,发挥引领辐射作用
典型性习题的立意高于常规性的习题,可以带动、辐射其他简单的、普通的知识点。教师要善于抓住知识中的要点,指向知识的典型所在,设计具有代表性的习题,让学生通过练习明晰重点、把握关键知识,达到触类旁通的目的。
例如,在教学“多边形的面积”后,一位教师设计了如下习题:在点子图(图略)上画一个平行四边形,然后想一想、议一议:(1)平行四边形的面积公式是怎么推导的?(2)平行四边形、三角形和梯形的面积计算有什么联系?
这样一道题目,是基于平行四边形、三角形和梯形的面积计算而设计的,是对零散知识的综合整理。学生在解决问题的过程中,既发现了三种图形的面积计算公式的推导过程都应用了转化的数学思想,又发现了当梯形的上底和下底相等时,梯形变成了平行四边形;梯形的上底等于0时,梯形就变成了三角形。三种图形都可以用“(上底+下底)×高÷2”计算他们的面积。
四、彰显整体性,架构知识体系
事物彼此之间有着紧密的联系。数学也一样,虽然教材的编写是把各个知识点分散在各年级,但各知识点有着紧密的前后关联性。教师要立足知识的整体角度,通过习题设计把零散的知识串起来,让学生在解决问题的过程中串起各知识点,架构起完整的知识体系。
例如,在教学“扇形统计图”后,笔者综合之前教学的“百分数”设计了如下作业:观察下图,(1)该小区一天产生的生活垃圾有多少千克?(2)该小区一天产生的其他垃圾有多少千克?(3)把两幅统计图补充完整。
这道题需要学生有较强的读图能力和综合分析能力,解决第一个问题要从两个统计图中找到相对应的信息,可以通过图中提供的厨余垃圾的数量和所对应的百分比计算出小区一天的生活垃圾总量;还可以通过图中提供的有害垃圾的数量和所对应的百分比求出答案。解决第二个问题,学生可以先通过小区一天的生活垃圾总量求出可回收垃圾的数量,再求其他垃圾的数量,也可以先求出其他垃圾所占的百分比,再求出具体的数量。这样的习题,既有数学与科学的学科融合,又有百分数与扇形统计图的知识综合,更有画图与解决问题的方法整合,沟通了零碎知识的内在联系,丰富了解决问题的策略,有效地提高了学生的综合素养。
五、增强开放性,培养创造能力
教师要根据学生的认知水平、知识的特点合理设计开放性的作业,从而激发学生的学习兴趣,促进学生发散思维能力和灵活解决问题能力的发展。
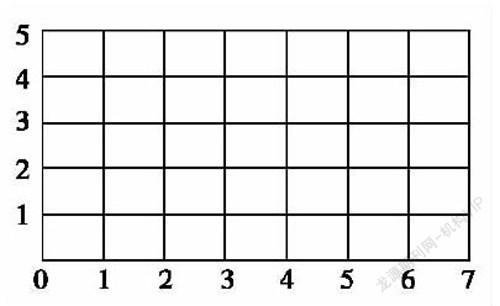
如在教学“用数对确定物体的位置”后,笔者设计如下习题:已知A(1,2)、B(3,4)、C(5,4)是梯形ABCD的三个顶点,请用数对在右图中标出第四个顶点D的所有可能在的位置。
本习题先让学生根据所给数对找出点A、B、C,考查了学生对数对基本知识的掌握情况,又让学生根据梯形的特征,用数对表示出点D在图中所有可能的位置。学生不仅可以以水平方向的线段BC为底,在A点所在的横线上取一个D点,使AD大于或小于BC,形成相对标准位圖的梯形ABCD。学生还要会打破思维定势用斜线AB为底,在与AB平行且经过C点的线上找出D点,使CD大于或小于AB,形成非常规位图的梯形ABCD。这样的开放性习题,既有对基础知识的考查,又能帮助学生突破思维定势的束缚,学生在拓宽解题思路的同时,思维的灵活性和创造性都得到了发展。
(作者单位:福建省德化县尚思小学 本专辑责任编辑:王振辉)
