在多样化策略中感受优化思想

杨曼玉

“找次品”是人教版五下“数学广角”的内容，其教学目标旨在让学生通过找次品这一数学活动，学会运用猜测、推理、归纳的方式来分析问题并解决问题。同时，通过在解决问题的多样化方法中找出最优的解决方案，让学生感受数学解题策略的多样性及优化思想。

一、初步感知找次品的原理

找次品的学习对初次接触的学生有一定难度，因此教学应遵循化繁为简、从特殊到一般的方法，从简单的问题入手，让学生初步感知找次品的含义与基本思路，激发学生的学习兴趣。

在课堂上，教师拿出准备好的天平（没有砝码）和3盒饼干，告诉学生其中有一盒偏轻的是次品。教师提问：“如何利用天平找出次品？”然后让学生利用天平进行操作。学生边操作边说：“先随意把其中2盒饼干放在天平上，天平出现不平衡，天平左边向上倾斜的话，左边的就是次品。”教师提问：“如果天平平衡，次品怎么找？”生1：“如果天平平衡，从天平上拿下来一盒，再把另一盒放上去称。”生2：“我觉得不用再称了，如果天平平衡，那么天平外的就是次品了。”教师借助学生的操作与回答进行引导，学生感受找出次品的推理过程，理解找次品的基本思路。通过思考与实际操作，让学生明白次品出现的地方可能在天平的左边，可能在天平的右边，也可能在天平的外边。教师小结：当物品被分为了3份，可分别用左、右、外来标识，在数学上称为“三分法”。

二、体验找次品中分法的多样化

在教学过程中，要注重培养学生自主探究的学习能力，让学生经历猜想、探索、验证等过程，感受解决问题策略的多样化。因此，在找次品的教学过程中，应当让学生自己独立思考探索，感受方法的多样化。

教师课件出示8个零件，告诉学生其中有一个偏重的零件是次品。教师引导：“用你喜欢的方式，将你的分法、称的次数以及推理过程记录下来。”学生探究后进行汇报，生1：“把8个平均分成2份，用天平称出哪一边重，再把向下倾斜的4个分成2组，用天平称出哪一边重，再把向下倾斜的2個拿去称，向下倾斜的一边是次品，需要称3次。”生2：“把8个分成3份，即8（3，3，2），天平两边各放3个，天平外剩2个，会出现2种可能。如果平衡，将天平外的2个拿去称，天平重的那边是次品，共称2次;如果不平衡，天平重的那边3个再称，将其中2个分别放在天平两侧，如果平衡，则天平外的是次品，如果不平衡，则天平重的那边是次品，共需称2次。”

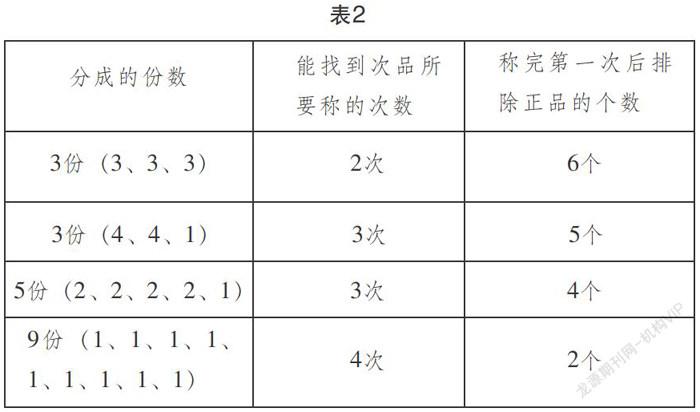
这一环节学生展示了不同分法的推理过程，明白在多种的分法中，分的份数不同，称的次数也有所不同。为了让学生更好地分析与比较不同的分法，教师让学生利用表格将8个零件的多种分法进行归纳，具体如下表。

教师提问：“哪种分法称的次数最少？”学生回答：“8（3，3，2）称的次数最少。”教师：“为什么8（3，3，2）只要称2次就能找出次品，8（4，4）要称3次？”生1：“8（3，3，2）称一次后，次品在3个或2个里面，再称一次就可以找到了，而8（4，4）称一次后，次品在4个中，4个至少还要称2次才能找出次品。”借助该生的回答，教师引导学生将8（3，3，2）与其他分法进行比较，明白这种方法称一次就可以将次品确定在更小的范围内，为理解三分法是最优分法打下基础。

三、发现规律，找出最优分法

优化思想是一种重要的数学思想。在解决“找次品”的问题中，除了让学生对多种分法进行对比分析，还要培养学生解决问题的优化意识。

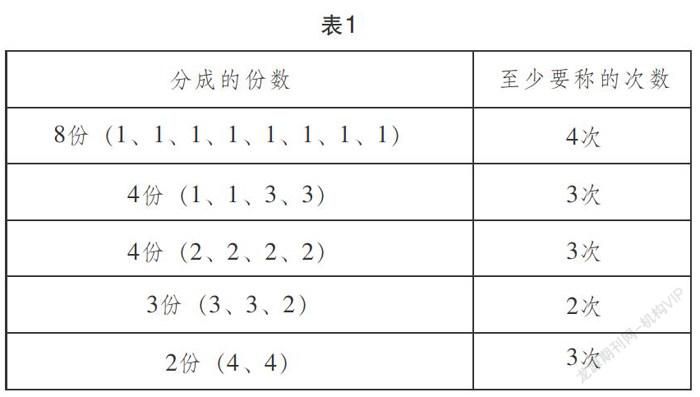
在教学从9个零件中找出次品这一环节时，教师提问：“需要利用天平称几次才能保证找到次品，怎么称？四人为一组，利用教材中例2的表格将所有的分法记录下来。”在进行小组合作之前，教师先教学“至少”和“保证”的含义，让学生明白“至少”是指在最不幸运情况下保证找出次品的方案中，称的次数是最少的。经过小组的汇报，教师将9个零件的分法用表格（表2中的第1列）的形式呈现出来。教师提问：“哪一种分法称的次数最少？”学生回答：“9（3，3，3）称的次数最少。”教师继续提问：“前面比较过8（3，3，2）和8（4，4），现在思考一下，为什么9（4，4，1）比9（3，3，3）多称1次？”学生回答：“9（4，4，1）称一次后，次品在4个或1个中，但要考虑最不幸运的情况下，4个至少还要称2次才能找出次品，而9（3，3，3）称一次后，次品在3个中，只要再称一次就可以找出次品了。”教师：“第一次称完后，次品的范围越小，称的次数就越少，要怎样才能把次品范围最小化？”学生回答：“那第一次称的时候，排除的正品要多。”教师：“现在完成表格中新增加的一列（表2中的第3列）。”通过对教材表格进行“加工”，学生很明显地看出，确保找到次品所要称的次数最少，就是在称完第一次后排除正品的个数要最多，排除的正品多，找到次品的可能性也就大了。

教师提问：“8（3，3，2）和9（3，3，3）都是最优的分法，它们有什么相同点？”生1：“都是分成3份，而且都称2次。”生2：“9（3，3，3）是平均分，8（3，3，2）虽然不是平均分，但每1份的数量都相差不大。”生3：“它们第一次称完，排除的正品都是最多的。”教师提问：“到底怎么分，才能使称的次数最少，又能保证找到次品？”生1：“我认为要分成3份，天平上放2份，天平外放1份。”生2：“分成3份，要平均分，这样称的次数就少。”教师：“像8就不能平均分成3份？”生3：“我觉得要分成3份，要尽量平均分，这样第一次称完后，才能将次品的范围缩到最小范围，称的次数就少。”教师根据学生的回答及时小结，让学生明白并理解三分法是找出次品多样化的最优分法。

（作者单位：福建省连江县蓼沿中心小学）