ISEGST在非线性RC结构瞬时频率识别中的应用
2021-12-02沈中祥袁平平
沈中祥,袁平平,刘 义
(1.江苏科技大学 土木工程与建筑学院,江苏 镇江 212003;2.河海大学 港口海岸与近海工程学院,南京 210098;3.江苏扬子江船业集团公司,江苏 靖江 214532)
在RC结构中,由于钢筋、混凝土的材料非线性特性,结构的振动响应一般为非平稳信号,因此其频率具有时变特性[1-9]。准确地识别出非线性RC结构在振动荷载作用下的瞬时频率等特征,对结构的健康监测、状态评估和维修加固等起着至关重要的作用[10]。近年来,时频分析技术在信号处理领域显示出了巨大的潜力,已成为一个新的研究热点。然而,以往的时频分析方法都存在一定的不足,例如短时傅里叶变换[11](short-time Fourier transform,STFT)的窗函数宽度固定不变,使其时频分析能力较弱。在处理多分量复杂信号时,Wigner-Ville分布[12](Wigner-Ville distribution,WVD)会受到交叉项的影响而产生虚假模态。连续小波变换[13](continuous wavelet transform,CWT)在处理非平稳信号时也可能会产生模糊的时频脊线,这将不利于瞬时频率的提取。
为了使时频脊线的能量更集中,瞬时频率的识别效果更精准,Stockwell等[14]将STFT和CWT相结合,提出了S变换(S-transform,ST)。ST克服了STFT窗口时宽不变的缺陷,能根据频率的变化调整分析时宽和提供直观的时间频率特征。随后,一系列针对窗函数的改进算法,即广义S变换(generalized S-transform,GST)被提出。其中,Zidelmal等[15-16]对GST的窗函数进行了改进,并通过能量集中度(concentration measure, CM)[17]给出了GST中窗函数的参数优化算法。为了提高聚集性,Daubechies等[18]提出了同步挤压变换(synchrosqueezed transform,SST),该方法以小波变换为基础,通过对时频周围的能量进行挤压,有效提高了时频能量的集中度。赵朋[19]提出了基于改进S变换时频谱重排的时变结构瞬时识别方法。Yu等[20]以SST为基础,进一步提出了多重压缩变换(multi-synchrosqueezing transform, MSST),该方法通过多次压缩变换,有效地提高了时频能量的聚集性。同时,Yu等[21]还借鉴SST算法,提出了同步提取变换(synchroextracting transform,SET)。随后相关学者对其不断进行改进,使SET的时频分辨率显著提高[22-23]。Chen等[24]提出了基于GST的高精度时频分析同步挤压算法,即同步挤压广义S变换(synchrosqueezing generalized S-transform,SSGST)。康佳星[25]将SET和GST联合起来,提出了同步提取广义S变换(synchroextracting generalized S-transform,SEGST),并将其成功应用到地震信号分析中。
本文采用了一种改进的广义S变换(improved generalized S-transformation, IGST),并结合能量CM原理推导了窗函数参数的优化算法,最后联合SET引入了ISEGST。为了探究ISEGST对非线性RC结构瞬时频率的识别能力,在数值模拟方面,本文基于OpenSees结构分析软件,建立了一个三层RC框架结构,并计算其在地震作用下的动力响应,通过ISEGST对其加速度响应信号进行时频分析获取瞬时频率,从而验证所提方法的可行性。试验方面,应用ISEGST对某七层剪力墙振动台试验数据进行时频分析和瞬时频率提取,进一步验证该方法的实用性。
1 理论知识
1.1 改进广义S变换
ST是地球物理学家Stockwell于1996年在STFT和CWT基础上提出的一种时频分析方法,其特点是引入了宽度和频率成反比的高斯窗,其表达式为
(1)

ST具有完全可逆性,其逆变换为
(2)
对ST的窗函数进行改进,得到GST为
(3)
(4)
将改进后的窗函数代入到ST中,得到IGST为
特别地,当p=0时,IGST退化为GST;当m=1,p=0,r=1时,IGST则退化为传统的ST。
通过转换,得到IGST在频域的表达式为
(6)
1.2 参数优化算法
GST中的关键问题是如何选择窗函数的参数,IGST同样面临着这个问题。本文采用能量CM的方法进行计算
(7)
将IGST数据进行归一化处理
(8)
优化问题可以表示为
(9)
优化问题的约束条件与所分析窗口的宽度范围有关,窗口不应太窄而改变时间分辨率,但也不能太宽而影响频率分辨率,即
(10)
式中:Ts为采样周期;f∈[fmin,fmax];fmin=1 Hz;为满足奈奎斯特采样定理,这里fmax的值取采样频率的一半。式(10)可简化为
(11)
本文中,参考Zidelmal等和Moukadem等的研究,令m∈(0,3],p∈[0,3],r∈[0,1],K=10,L=1 000。所以,最终设置的优化问题为
(12)
式(12)可以看作是多元函数的优化问题,即在一系列约束条件下,寻找一组参数值,使某个或某一组函数的目标值达到最优。通过优化算法对上述问题进行求解即可得到IGST窗函数的参数值。
1.3 同步提取算法
借鉴SET原理,可以得到ISEGST为
SEIGST(τ,f)=IGST(τ,f)·δ(f-ωi(t,f))
(13)
式中:δ为同步提取算子,即
(14)
通过IGST(τ,f)来计算每一个时频系数对应的瞬时频率ωi(t,f)
由式(15)可得
(16)
其中,


实际应用时,考虑到计算误差,可以采用式(18)近似计算同步提取算子δ,即
因此,ISEGST具体为
ISEGST(τ,f)=
(19)
式中,Δf为频率间隔,一般可取为1。
2 数值模拟
2.1 模型计算
本文设计了一个三层非线性钢筋混凝土框架结构,其尺寸如图1所示。混凝土板厚度为120 mm,柱构件截面尺寸为500 mm×500 mm,梁构件截面尺寸为500 mm×250 mm,如图2所示。混凝土类型为C30,钢筋型号为HRB400,其材料本构具体如图3所示。楼面恒载为3.5 kN/m2,活载为2 kN/m2,采用1940年EL-Centro地震波对结构进行X轴方向的激励,地震波最大峰值加速度为2.2 m/s2。采用OpenSees软件对结构进行分析,从而得到结构的动力响应。在OpenSees模拟中,混凝土本构关系采用Concrete02,钢筋本构采用Steel01,钢筋和混凝土的本构关系见图3。箍筋能够约束混凝土,提高混凝土的抗压强度。考虑到箍筋对混凝土强度的影响,本文将梁和柱的核心混凝土的强度提高了40%。
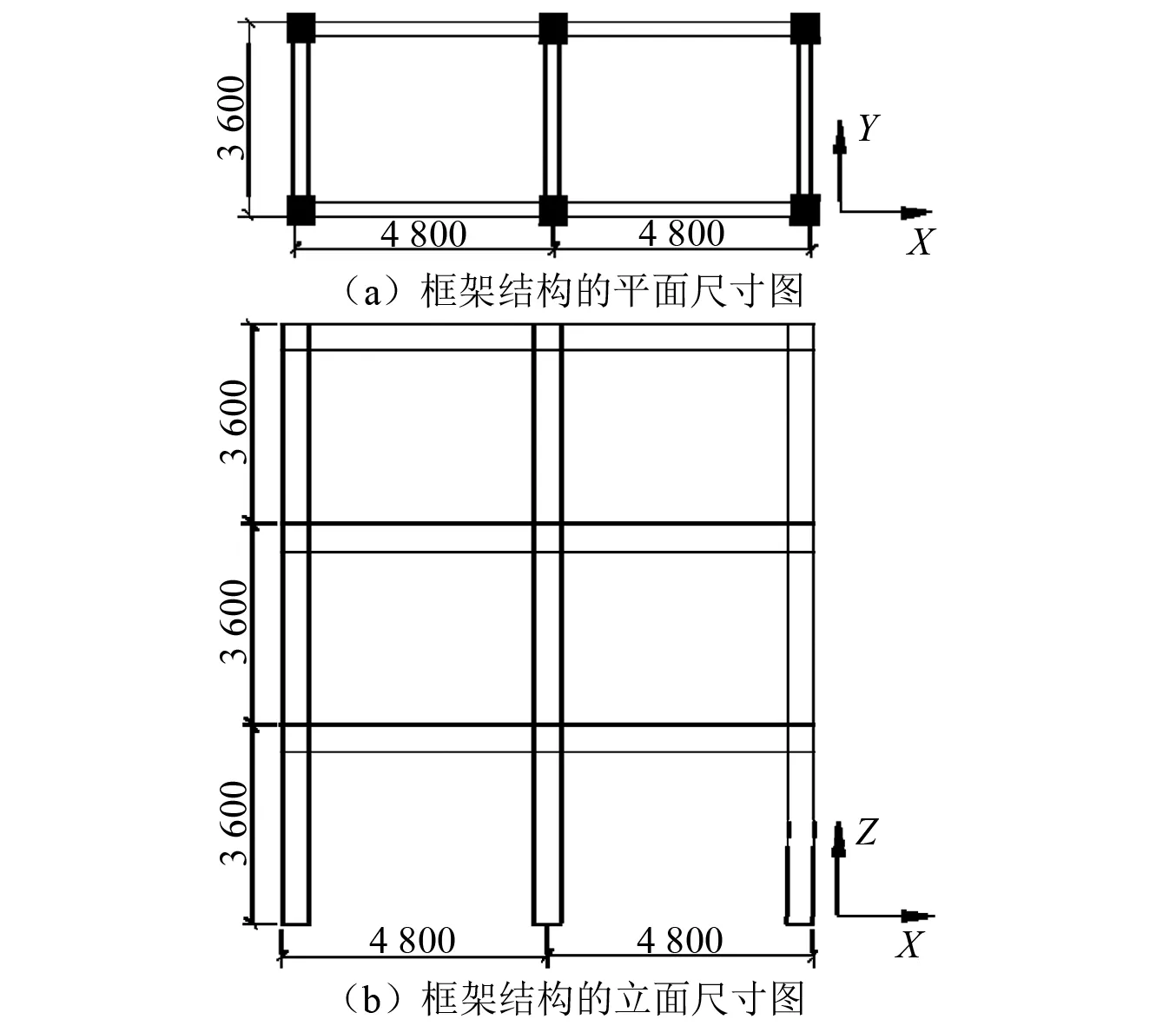
图1 框架结构的平面及立面布置图(mm)
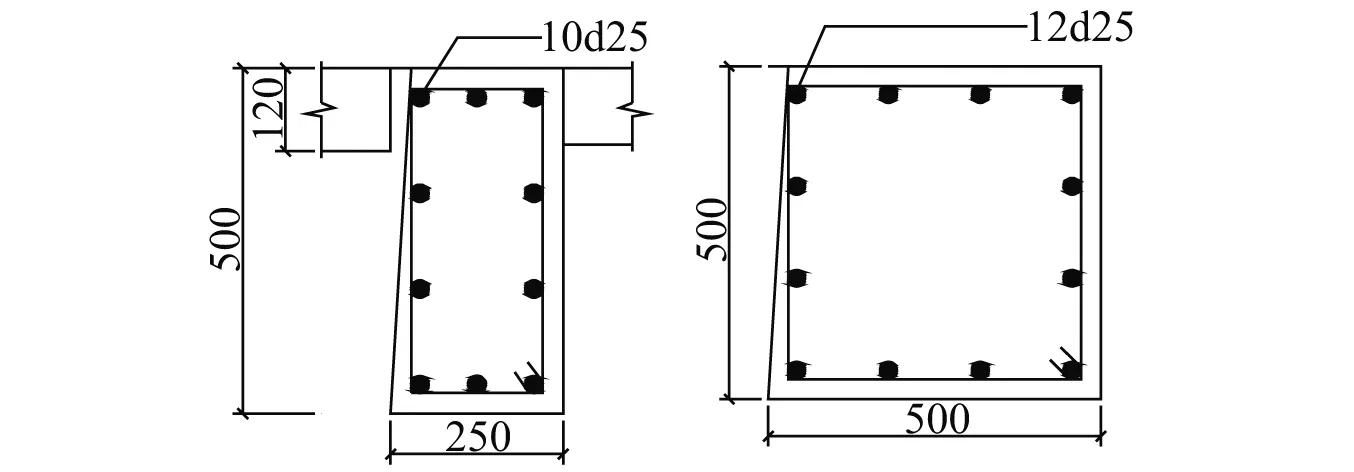
图2 梁、柱截面配筋(mm)

图3 材料本构图
2.2 瞬时频率提取
通过OpenSees软件计算分析,得到框架结构顶层中间节点的加速度响应曲线,如图4所示,选取该加速度响应信号为研究对象,通过STFT、SST、SET、IGST、ISEGST等五种方法对其进行时频分析研究。在IGST中,窗函数的参数m=1.346 9,p=3,r=0.917。
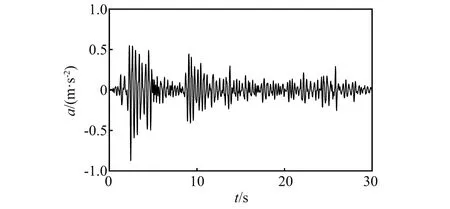
图4 框架结构的加速度响应
时频分析的结果如图5所示。对比图5(a)和图5(d)可以看出IGST的能量聚集性更高,这更利于ISEGST的频率提取。从图5(b)、图5(c)和图5(e)中可以看出SST的时频分析结果较差,SET和ISEGST的时频分析结果较好,而且ISEGST的结果更加平滑,时频能量的聚集性更高。

图5 框架结构的时频分析结果
框架结构的频率识别结果如图6所示。可以看出,三种方法都能有效识别出结构的瞬时频率。SET的识别结果波动较大,SST的识别结果与ISEGST的识别结果几乎相等,但是,ISEGST的频率识别曲线更加平滑,波动较小,结果更加准确。

图6 框架结构频率识别结果
3 试验验证
为了进一步研究ISEGST对实际结构运动响应信号的瞬时频率识别效果,本文引用加州大学圣地亚哥分校(USCD-NEES)Panagiotou等[26]设计完成的七层RC剪力墙振动台试验数据进行了时频分析,其中地震波加速度响应如图7所示,实测的结构加速度响应如图8所示。

图7 施加于剪力墙的地震波

图8 剪力墙结构的加速度响应
对所得加速度响应信号进行时频分析,结果如图9所示。其中,IGST的窗函数参数m=3,p=2.137 9,r=0.575 9。通过图9(b)、图9(c)、图9(e)可以看出IGST的时频分析结果更加平滑,效果更为理想。

图9 剪力墙的时频分析结果
通过极值法对SST、SET、ISEGST时频分析结果的频率进行进一步提取,提取结果如图10所示。可以看出SST的时频分析结果较差,SEI和ISEGST的时频分析结果更为理想。但是,相对于SET, ISEGST的结果波动较小,平滑性更高。
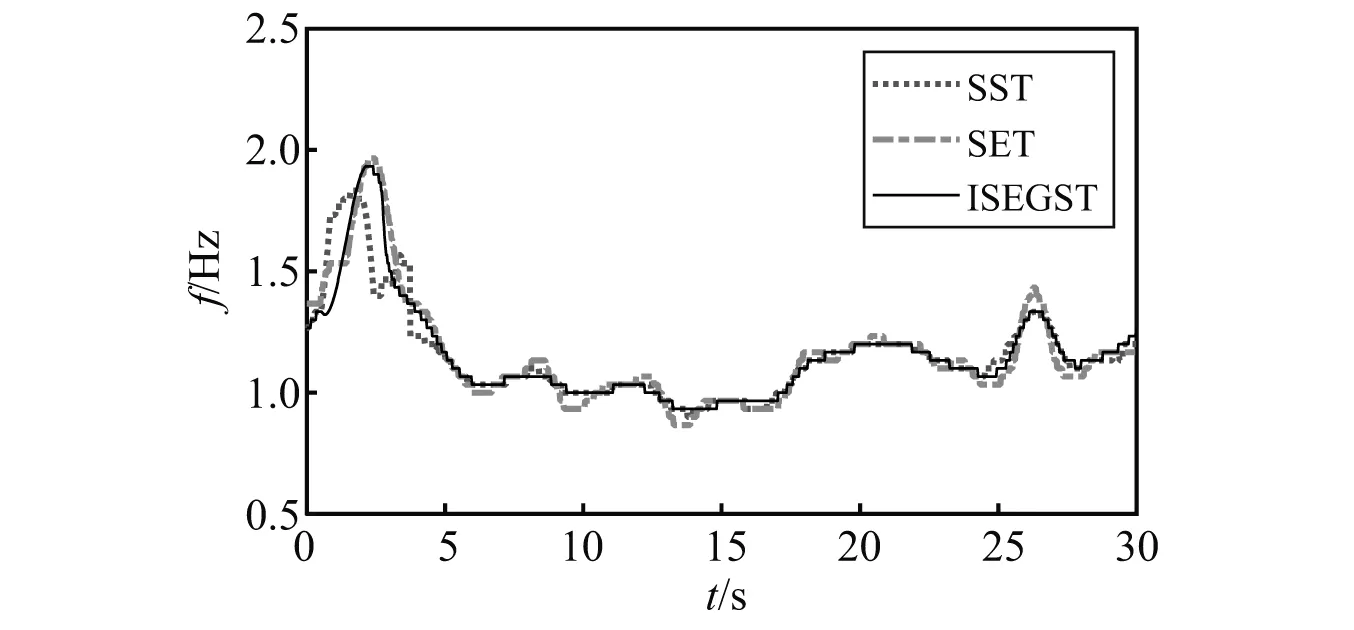
图10 剪力墙结构的频率识别结果
4 结 论
本文将ISEGST应用到非线性RC结构瞬时频率识别中。对三层RC框架结构和七层剪力墙结构的加速度响应进行时频分析,从而提取结构的瞬时频率。数值模拟和试验结果表明ISEGST具有以下优点:
(1)结合CM原理和优化算法,可以计算得到IGST中窗函数的调节因子参数,有效地提高了IGST的计算效率和精度。
(2)延续了IGSE和SET的优点,ISEGST识别出的瞬时频率曲线更加平滑、准确,是一种准确性较高的非线性RC结构瞬时频率识别方法。
