基于SVDD去除异常值的水下目标定位方法

庞菲菲，温祥西，王晓华

(1.西安工程大学 电子信息学院，西安 710048；2.空军工程大学 空管领航学院，西安 710051)

对水下目标的精确定位可以为水下目标的安全航行、打捞救生以及海洋资源开发提供基础，成为当前研究的热点[1-5]。基于方位角的定位方法根据多个节点估计的方位角对目标进行定位，是一种经典的被动无源定位技术，广泛应用于水声传感网络中。受复杂多变的水声环境、多径效应、硬件失效、冲击噪声等的影响，节点测量的方位角可能会严重偏离真实的方位角，即出现异常值的情况，对目标定位精度造成严重影响[6]。

针对异常值出现的目标定位问题，现有的解决方法主要有两种：一种是采用基于鲁棒的统计估计方法以减小定位过程中异常值引起的负面影响；另一种是筛选出异常值并在定位时将其剔除，避免其对定位的影响。文献[7]使用鲁棒的统计估计方法，将lp范数最小化作为优化目标函数，然后采用迭代加权辅助变量估计方法进行求解。该方法需要迭代运算，不能得到解析解，运算量较大。文献[8]使用鲁棒最小二乘准则构造目标函数，通过求解广义信赖域子问题得到准确解，以减轻异常值对定位偏差的影响。文献[9]通过k-means聚类算法排除误差较大的测距信息，最后利用剩余距离信息进行目标定位。该方法可在不增加通信开销的前提下，得到更精确、容错性更高的定位方法。文献[10]认为异常值严重偏离了其余节点的观测信息，结合几何学和统计方法提出了到达时间差的异常信息检测方法。文献[11]利用长基线/超短基线组合系统，并采用k-means聚类算法和决策融合对多种定位参量中的异常值进行检测，通过识别并去除异常值保证了定位系统的可靠性。这种剔除异常值的方法可以从根源上避免异常信息对定位结果的影响。

文献[12]指出:测向线所给信息是目标定位和分选的全部依据；一条测向线说明目标可能在离线很近的地方，而很少可能在离线很远的地方。因此，当所有节点测量的方位信息都较为准确时，方位交线产生的目标初始估计位置会紧密分布在目标真实位置附近；而当节点观测的方位信息出现异常时，异常值对应的目标初始估计位置会远离于其余初始位置。利用这一分布特征，本文针对异常值出现的情况，提出了基于支持向量数据描述(support vector data description，SVDD)的目标定位方法。该方法将目标定位与异常值识别有机结合，首先使用SVDD对方位交线方法所产生的目标初始估计位置进行一分类处理，然后利用位于超球面外的外点识别出异常值并将其剔除，最后利用剩余的方位信息对目标进行定位。本文方法可以有效筛选出异常值，避免异常值对定位精度的影响。

1 观测模型

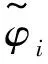
图1 方位观测模型

(1)

当有异常情况出现时，第i个节点观测的方位信息利用高斯混合模型表示

(2)

式中：τi∈{0,1}为独立同分布的Bernoulli随机变量，代表是否有异常值出现，若有异常值则τi=1，反之τi=0，假设异常值出现的概率为pi=Pr{τi=1}；mi为在[-π,π]均匀分布的冲击噪声。

2 基于SVDD在异常值出现时的目标定位方法

2.1 目标位置的初始估计

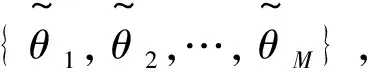
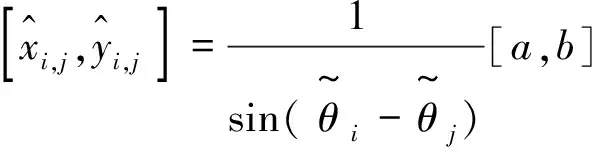
i,j=1,2,…,M且i≠j

(3)

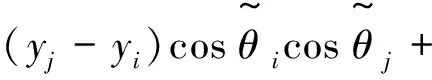
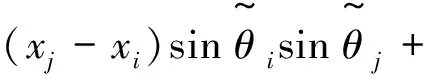
(4)

式中，[xi,yi]，[xj,yj]分别为第i，j个节点的坐标。

2.2 目标位置初始估计值的分布特征

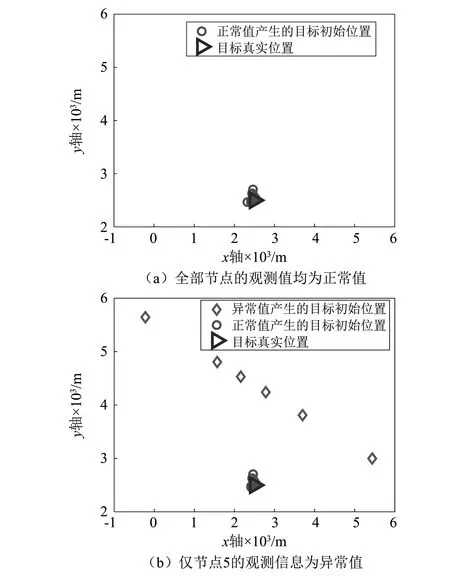
图2 目标位置的初始估计分布

因此，可以根据目标位置初始估计值的分布特征筛选出异常值，将其剔除后再利用其余正常观测方位信息对目标位置进行估计，这种方法可以从根本上避免异常信息对目标定位精度的影响。从所有初始估计值中筛选离散点(异常值引起的初始估计值)的过程可由单分类算法来实现。SVDD方法作为一种单分类器，可在给定的一个数据集周围确定一个闭合的超球体，使该超球体能够几乎包含所有数据样本的最小超球体，因此本文利用SVDD方法划定类别边界进行离散点检测。

2.3 基于SVDD的目标定位方法

支持向量机由Vapnik[14]于20世纪90年代提出，最初用于解决二分类问题。随后，Tax等[15]将统计学习理论通过支持向量机的形式扩展到无指导学习领域，提出了一种新的数据描述方法——SVDD方法。SVDD方法是一种单分类方法，其基本思想是：通过非线性变换将目标样本映射到一个高维的特征空间，在高维空间建立一个封闭而紧凑的最小超球体，权衡超球体半径和它所包含的样本映像的数目，使其包含的样本映像数量最多[16]。

由于异常值的影响，数据集的样本特征不是集中分布的，而是存在离散的数据分布。这些样本的分布存在以下三种可能：

(1)对应样本Xi到超球体球心的距离小于R，即该样本在球体内，称为内点；

(2)对应的样本Xi位于超球面上，称为支持向量；

(3)若Xi落在超球体外，称为外点(即离散点)。

外点是由异常值引起的，由于每个样本都对应了两个节点的测量值(参见式(3))，因此可由外点反推出异常值。将异常值剔除后，使用剩余的方位信息求解得到最终的目标位置。

基于SVDD去除异常值的目标定位方法具体步骤为：

步骤1每个节点分别对目标进行方位估计，利用方位交线方法，得到N个交点X1，X2，…，XN，将其作为样本集；

步骤2利用SVDD方法对样本集进行分类，检测出外点；

步骤3找出每个外点所对应的两个方位信息序号，并统计序号的出现次数；筛选出现次数大于等于t的所有序号，将这些序号对应的观测值视为异常值，假设筛选出的异常值个数为n；

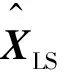
(5)

其中，

(6)

在所提的方法中，t起到了一个门限的作用，即：如果外点对应的方位统计次数大于等于t，则认为该方位信息为异常值。如果t的值越大，则认定某个方位信息为异常值的门限越高，即有可能识别不出异常值；反之，门限越低，意味着可能会将正常方位信息误判为异常值，出现虚警的情况。在实际应用中，t的大小与异常值出现的概率pi、方位估计误差的标准差σi有关。当pi增大时，外点的个数也会增加，t的值应该适当增大；反之，t的值应适当减小。另一方面，当正常方位估计误差的σi比较大时，利用该方位信息得到的目标初始估计位置会越偏离目标真实位置，从而被SVDD方法识别为外点的概率也会增加，因此需要适当增加t的值，避免造成误判；反之，可适当减小t的值，降低门限，提高异常值的识别概率。

3 仿 真

本文分别采用LS估计方法、基于k-means聚类算法的定位方法与本文所提基于SVDD方法去异常值后使用LS(LS after removing unreliable measurements based on SVDD，SVDD-LS)定位方法进行定位精度比较。其中，LS估计方法是使用所有观测值、利用LS估计方法得到目标位置；基于k-means聚类算法的定位方法是指先采用k-means聚类算法找出异常值并将其剔除，使用剩余观测值、利用LS估计得到目标位置，简称为基于k-means聚类算法去异常值后使用LS(LS after removing unreliable measurements based on k-means，k-means-LS)定位方法。定位精度选取均方根误差(root-mean-square error，RMSE)来衡量，计算公式为

(7)

3.1 仿真参数设置

假设M个节点随机均匀分布在5 000 m×5 000 m的区域内；目标位于[2 500 m,2 500 m]。每个节点方位估计误差ni的标准差σi都相等；每个节点出现异常的概率pi相等。SVDD方法中惩罚因子取0.2，选用高斯函数作为核函数，核带宽选取500。k-means聚类算法中聚类的个数为2，筛选类内元素个数最少的聚类个数为1。蒙特卡洛仿真次数为1 000。

3.2 定位精度比较

(1)pi对SVDD-LS方法定位精度的影响

当有10个节点，且每个节点方位估计误差的标准差均σi为1°时，图3比较了SVDD-LS方法在t的值分别为3，4，5，6时的RMSE随异常值出现概率pi的变化情况。当t=3，pi≥0.03和t=4，pi=0.11时的RMSE均超过了1 000 m，所以在图3中没有显示出来。

图3 均方根误差随异常值出现概率的变化情况

3.2.2σi对定位精度的影响

本节讨论方位估计误差的标准差σi对LS、k-means-LS和SVDD-LS这三种方法定位精度的影响。假设每个节点出现异常的概率pi=0.01。当M=10时，图4比较了LS、k-means-LS和SVDD-LS这三种方法的RMSE随σi的变化情况。其中，σi的值由0.5°逐渐增加到7°，步长为0.5°，SVDD-LS的两条曲线分别是在t的取值为4和6的情况下绘制的。本节将LS方法的定位精度作为对比基准，k-means-LS和SVDD-LS方法都与LS方法进行比较。

由图4可以看出，随着σi的增加，三种方法的RMSE都随之增加。当σi≤3°时，k-means-LS方法的RMSE有所减小；但是随着σi的进一步增大，k-means-LS的定位精度逐渐降低，其RMSE甚至超过了LS方法，这是由于σi越大时，目标初始估计位置会越来越偏离目标真实位置，使样本愈加离散，k-means聚类算法在这种情况下不能很好地准确识别出异常值，导致k-means-LS方法的定位性能越来越差。对于SVDD-LS方法，当t=4时，其在方位估计误差较小时(σi≤3°)的RMSE最低；在3<σi≤5的区间内，t=4和t=6两条曲线几乎重叠，此时定位精度接近；当定位误差增加到更大的值时(σi>5°)，目标初始估计位置的分布会更加分散，当门限t比较小时，容易出现误判的情况，造成t=4对应的RMSE快速增加，当t增加到6时，SVDD-LS方法的RMSE最低，仍能表现出较好的定位性能。

图4 均方根误差随方位估计误差标准差的变化情况

3.2.3M对定位精度的影响

当pi=0.01时，图5比较了LS、k-means-LS和SVDD-LS三种方法的RMSE随节点个数M的变化情况，其中，图5(a)中的参数设置为σi=1°,t=4，图5(b)中的σi=4°,t=9。

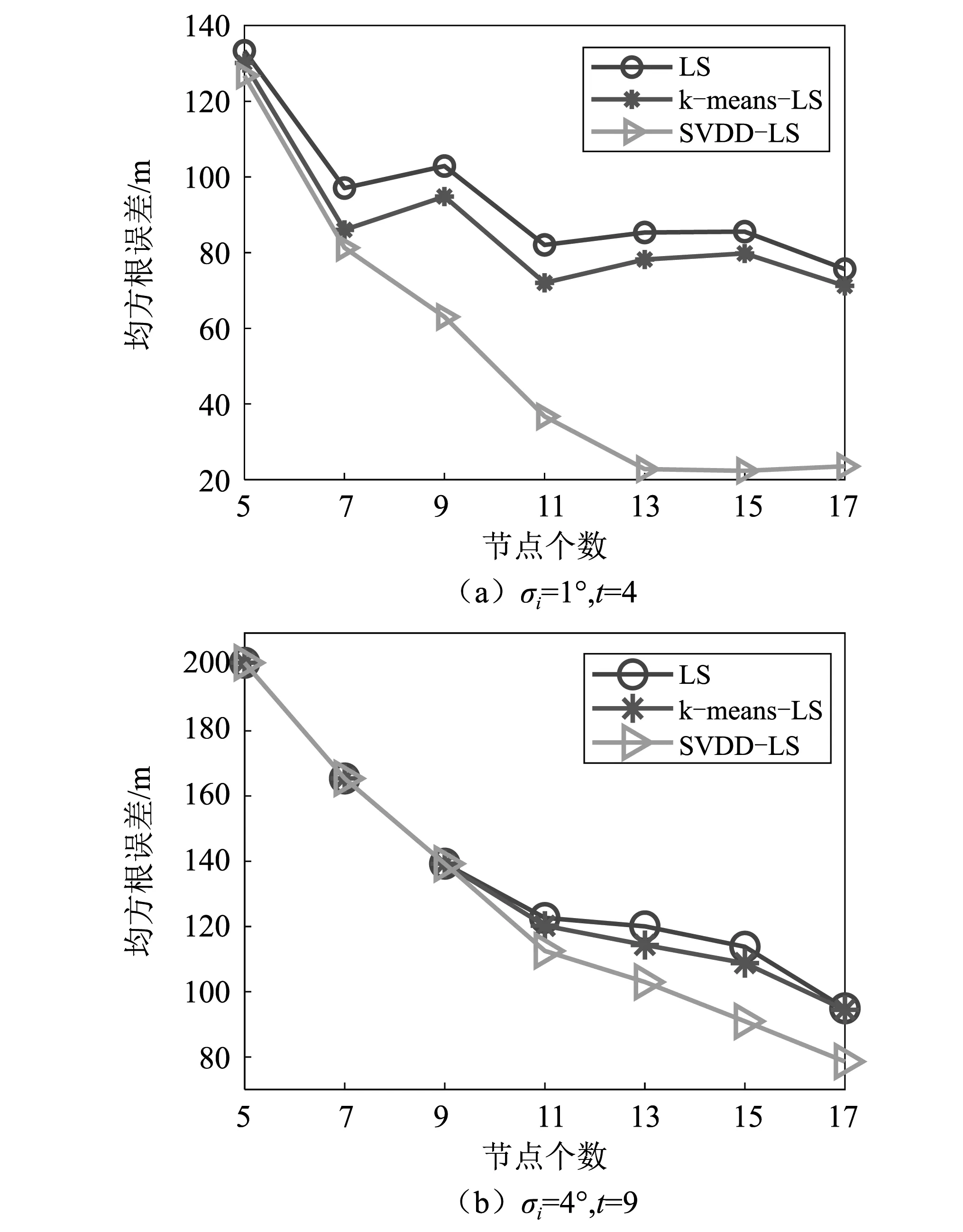
图5 均方根误差随节点个数的变化情况

由图5可看出，当节点个数由5逐渐增加到17时，三种方法的RMSE都随之下降，但是LS方法的RMSE仍然是最大的，这说明异常值的出现使LS方法的定位性能下降，而通过剔除异常值的办法可以避免其对定位精度的影响，提高目标定位精度。在三种方法中，SVDD-LS方法的RMSE降幅最大，表明该方法可以有效提高定位性能。当异常值出现概率pi较小且一定时，M的增加意味着样本个数和内点个数的增加。如果σi较小，即使内点个数增加，但是其依然会较紧密地围绕在目标真实位置附近，SVMM-LS方法仍然可以较好地识别出外点，展现出较好的定位性能，见图5(a)；而当σi较大时，内点数量的增加会使样点分布更加分散，可通过适量调高门限t避免误判，使SVMM-LS方法维持较低的RMSE，见图5(b)。

4 结 论

本文针对异常值影响目标定位精度的问题，基于SVDD方法提出了去除异常值的目标定位方法。该方法利用“异常值产生的目标位置初始估计值远离真实位置、正常观测值产生的初始估计值接近真实位置”的分布特征，首先采用SVDD方法对外点进行检测从而筛选出异常值，然后在使用LS估计方法计算目标位置时将异常值剔除、仅使用其余正常观测值，因此可以从根源上避免异常值对定位精度的影响。仿真结果表明，该方法可以有效识别异常值，其定位精度优于LS和k-means-LS定位方法。