驻波声场中空化气泡之间的相互作用研究

马 艳，赵飞燕，姚 曦

(1.宁夏师范学院 物理与电子信息工程学院 纳米结构及功能材料工程技术研究中心，宁夏 固原 756000；2.陕西师范大学 物理与电子信息技术学院，西安 710062)

超声空化试验发现，声场中的气泡并不是均匀存在，而是形成一些稳定的气泡结构[1]，这些气泡结构甚至能够存在数秒，关于声场中气泡如何形成这样的稳定结构，目前理论上不清楚，但是，气泡之间的相互作用力是其形成的主要原因[2-4]，声场中气泡之间的相互作用力主要是指次Bjerknes力，是由两个相邻气泡之中的某一个气泡产生的“第二声场”使两个气泡之间产生的作用力。自次Bjerknes力发现之后，Crum[5]、Oguz等[6]和Mettin等[7]分别进行了有意义的研究工作，得到了气泡线性振动和非线性振动下，气泡之间次Bjerknes力的相关规律，为声场中气泡之间的相互作用提供了理论基础[8-10]，但是他们的研究都是建立在平面声场中[11-12]，而超声反应器中，由于反应器尺寸一定，所以不可避免的在超声反应器中会形成驻波声场[13]，驻波声场中气泡之间的相互作用力具有什么样的特征，对空化气泡的振动特性及气泡结构产生什么样的影响，这些问题是研究超声反应器中气泡空化效应的重要因素，也是研究超声反应器应用的重要途径。

本文基于Mettin等关于次Bjerknes力的基本理论，研究了超声反应器驻波声场中两个气泡的振动特征和两个气泡之间的次Bjerknes力的特征及影响因素，为驻波声场中泡群形成的气泡结构和空化效应提供了理论依据，也为超声反应器的应用提供了相关理论。

1 驻波声场中双气泡动力学方程

超声反应器中，入射声波可表示为

Pi=PAej(ωt-kx)

(1)

式中：PA为声压幅值；ω为声波角频率；k为声波波数；x为声场中的位置。假设入射声波在超声反应器中完全反射，根据声波的叠加原理，合成声场为驻波声场，合成声压可表示为

Pdr=2PAcoskxejωt

(2)

如果声场中的两个气泡在振动的过程中仍然保持球形，则气泡振动的动力学方程可以用Keller-Miksis方程[14]来表示，具体形式为

(3)

(4)

式中：R1和R2分别为任意时刻气泡1、气泡2的半径；d为两个气泡之间的距离；ρ为液体的密度；c为液体中的声速；Ps1可表示为

(5)

式中：P0为液体的静压力；σ为液体的表面张力；ν为液体的黏滞系数；γ为气体绝热压缩系数。声场中，两个气泡之间的相互作用力通常称为次Bjerknes力，可表示为

(6)

式中：〈〉为时间平均；F12为气泡1受到气泡2的作用力；V1和V2分别为气泡1、气泡2的体积，为了方便描述次Bjerknes力的方向，通常引入次Bjerknes力系数，其定义为

(7)

fB的正负代表了气泡之间的力为吸引力或者排斥力，如果fB>0，则两个气泡相互吸引，如果fB<0，则两个气泡相互排斥。

2 驻波声场中气泡的非线性振动与气泡之间的相互作用

本文的主要研究结果是基于双空化气泡的耦合振动方程式(3)和式(4)得到的，式(3)、式(4)分别是基于气泡1、气泡2半径的二阶非线性常微分方程，可通过数值迭代法得到它们的数值解[15-16]。本文采用的是软件MATLAB中基于四阶五级Runge-Kutta变步长算法，这种算法能够采用误差作为检测指标的闭环控制，既保证有较高的运算速度和计算精度，也能保证预期的数值稳定性[17]，是求解气泡非线性常微分方程数值解的重要方法。数值模拟中，气泡1、气泡2半径的二阶常微分方程的初始条件为R1(t=0)=R10,R2(t=0)=R20, dR1/dt(t=0)=0，dR2/dt(t=0)=0。

在下面的数值模拟中，我们假设两个气泡之间的距离保持不变，只考虑入射波实部对气泡的影响，在此基础上我们分别研究了入射波声压振幅为0.9×105Pa，驱动频率20 kHz的平面波声场和驻波声场中初始半径为2 μm的气泡的最大半径随声场位置的变化关系，如图1所示。图1中，曲线Ⅰ、曲线Ⅱ分别为驻波声场和平面声场中气泡最大半径随声场位置的变化曲线，数值模拟结果表明在驻波声场中，由于入射声波和反射声波的叠加，在不同的位置处，会出现驱动声压振幅的不同，不同位置处气泡的收缩振动和气泡的初始位置有关，处于驻波声场的声压波腹x=0，x=0.037，x=0.074(0，1/2声波长，1个声波长)附近的气泡能够做剧烈的收缩振动，气泡在声压波腹处的最大振动半径能够达到初始半径的42.72倍。而同样初始半径的气泡在平面声场中，由于驱动声压振幅与声场中的位置无关，因而气泡在整个收缩扩张过程中如曲线Ⅱ所示，不同位置处的气泡在收缩振荡过程中，气泡的最大扩张半径均相同，在驱动声压振幅为0.9×105Pa时，整个平面声场中一个驱动周期内，气泡的最大半径只有初始半径的1.41倍左右，说明小振幅驱动的平面声场中，气泡只在初始半径周围做微弱的收缩振动，不发生剧烈的收缩溃灭现象。上述研究结果表明：驻波声场中，由于声波的叠加，使声场中出现了声压振幅的变化，造成了声场的不均匀性，但也是由于声压的叠加，使小振幅驱动下在声压振幅极大值位置处的气泡能够剧烈振动，产生剧烈的空化效应。

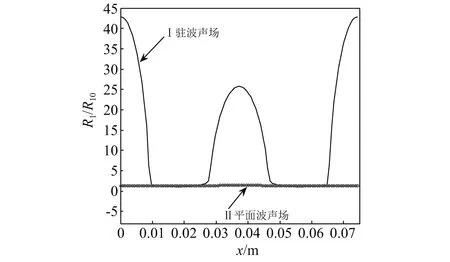
图1 气泡1的径向振动与气泡位置的关系曲线

当驱动频率为20 kHz 时，驻波声场和平面声场中，x=1/50 声波长，初始半径为2 μm，相距200 μm 的两个气泡组成的气泡对中气泡1的Rmax/Rmin随声压振幅的变化曲线, 如图2所示。Rmax/Rmin反映了气泡的能量转换能力[18]，对比可以看出，同样的入射波声压振幅下，驻波声场中的气泡在声压波腹附近具有更好的能量转换能力，能够在小振幅入射声压振幅下做剧烈的非线性振动，例如：当入射声压振幅只有0.85 Pa时，驻波声场中气泡的Rmax/Rmin即可达到89.09，而同样的入射声压下，平面声场中气泡的Rmax/Rmin只有1.467，此时的气泡只做微弱的收缩振动。驻波声场中，气泡能量转换能力的增强，源于驻波声场中，由于反应器的反射，使反应器部分区域的驱动声压振幅加倍，从而使气泡的非线性振动加强，但是数值模拟结果表明：在驻波声场中，气泡虽然能够在小振幅驱动声压下实现良好的能量转换能力，但仍然对驱动声压振幅有一定的要求。在上述条件下，我们发现当驱动声压振幅低于0.65×105Pa以下,气泡在驻波声场中波腹位置处不能做强非线性振动，气泡振动的最大半径与最小半径的比值在1.739左右，这表明在上述条件下，当驻波声场的驱动声压振幅低于0.65×105Pa时，即使处在波腹位置处的气泡也不能出现剧烈的空化现象。

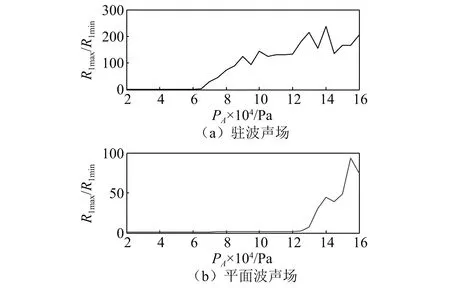
图2 气泡1膨胀收缩比随驱动声压振幅的变化曲线

声场中，两个气泡之间的相互作用力与气泡在声场中的位置有很大的关系，图3是驱动声压振幅为0.8×105Pa，驱动频率为 20 kHz的驻波声场和平面波声场中两个初始半径为2 μm，相距200 μm的气泡在一个声驱动周期内次Bjerknes力随气泡位置(1个声波长)的变化关系曲线图，如图3所示。图3中：曲线Ⅰ为驻波声场；曲线Ⅱ为平面声场；x=0.018 6(1/4声波长)和x=0.055 9(3/4声波长)为波节位置；x=0.037 2(1/2声波长)和x=0.074 5(1个声波长)为波腹位置。数值模拟结果表明：在驻波声场中，处于波腹位置处的两个气泡之间的相互作用最大，而波节位置处两个气泡之间的相互作用力趋于0，可忽略不计。具体原因是：处于声压波腹处的气泡能够做剧烈的振动，其产生的声场能对周围气泡产生更大的作用力，而位于声压波节位置处的气泡只能做微弱的线性振动，其对周围气泡的相互作用力也非常微弱，可忽略不计。数值模拟结果还表明：驻波声场中，一个声波长范围内，气泡位于0和1个声波长位置处，两个气泡之间的相互作用力最大，气泡位于1/2个声波长位置处，两个气泡之间的相互作用力次之；而在平面波声场中，在上述驱动条件下，两个气泡之间的次Bjerknes力近似为0。以上结果说明在小振幅驱动的声场中，声波的叠加使气泡的非线性振动增强，从而使气泡之间的次Bjerknes力增加，气泡之间的相互作用不能够忽略不计，这可能也是超声反应器中形成气泡结构的主要原因。

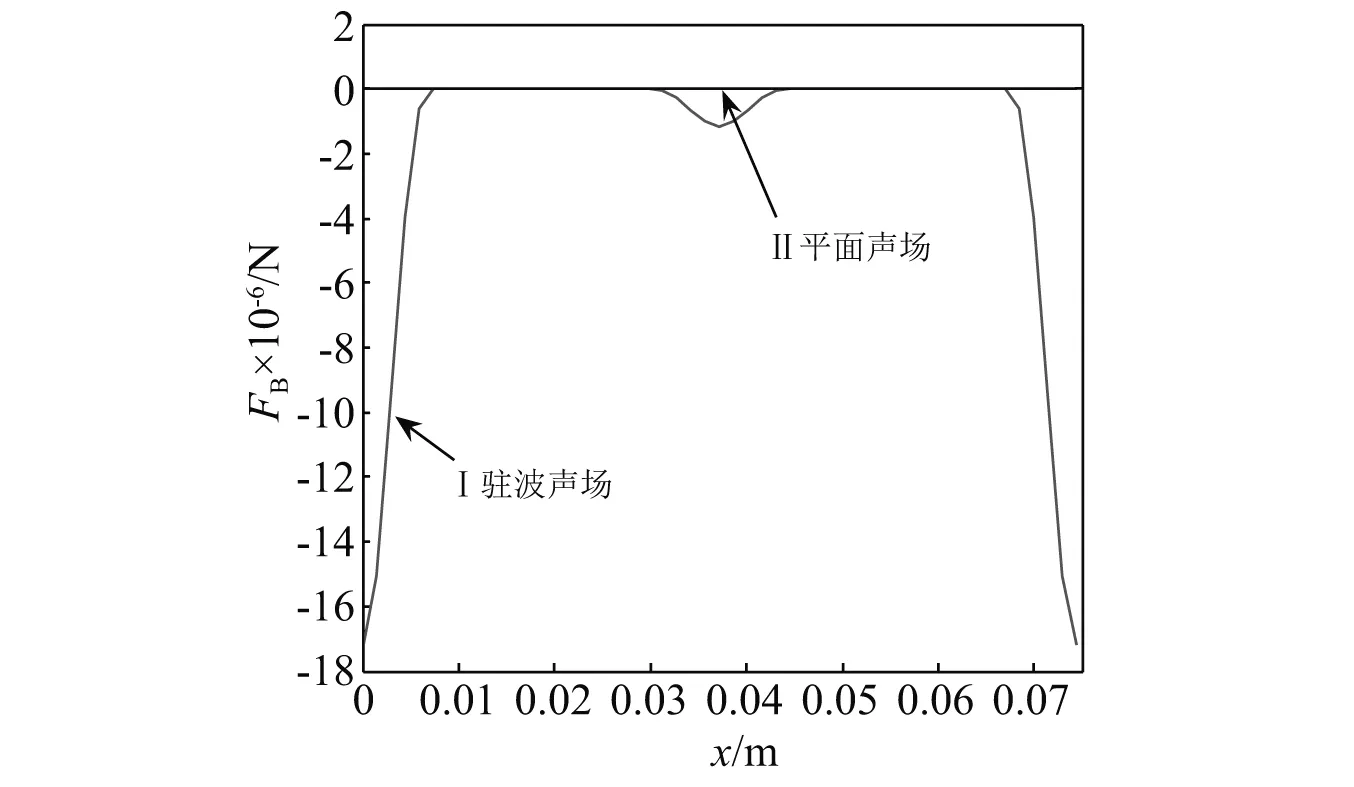
图3 气泡之间的次Bjerknes力随气泡位置的变化曲线

驻波声场中气泡1对气泡2的作用力F12与两个气泡的振动状态有关。驱动声压振幅为0.8×105Pa，驱动频率为20 kHz的驻波声场中，位于1/50个声波长位置处的两个初始半径为2 μm和3 μm的气泡的作用力F12和每个气泡的收缩振动速度与时间的关系，如图4所示，主要数值模拟结果如表1所示。在0.72个声驱动周期时，气泡1处于收缩状态，气泡2处于扩张状态，此时气泡1对气泡2的作用力F12为排斥力；在0.82个声驱动周期时，气泡1处于迅速扩张状态，气泡2处于扩张状态，此时F12为吸引力，计算结果表明：气泡的收缩振动速度越大，气泡1对气泡2的作用力越大。在平面波声场中，同样的驱动条件下，两个初始半径为2 μm和3 μm的气泡之间的瞬时作用力也遵循同样的规律，如图5所示。在0.01个驱动周期时，气泡1的振动速度为-1.67 m/s，表明气泡1处于收缩状态，气泡2的振动速度为1.31 m/s，表明气泡2处于扩张状态，此时气泡1对气泡2的作用力F12为1.76×10-11N，为排斥力，当两个气泡都处于扩张或者收缩状态时，F12为吸引力，而当两个气泡中一个处于扩张状态，另一个处于收缩状态时，气泡1对气泡2的作用力为排斥力。

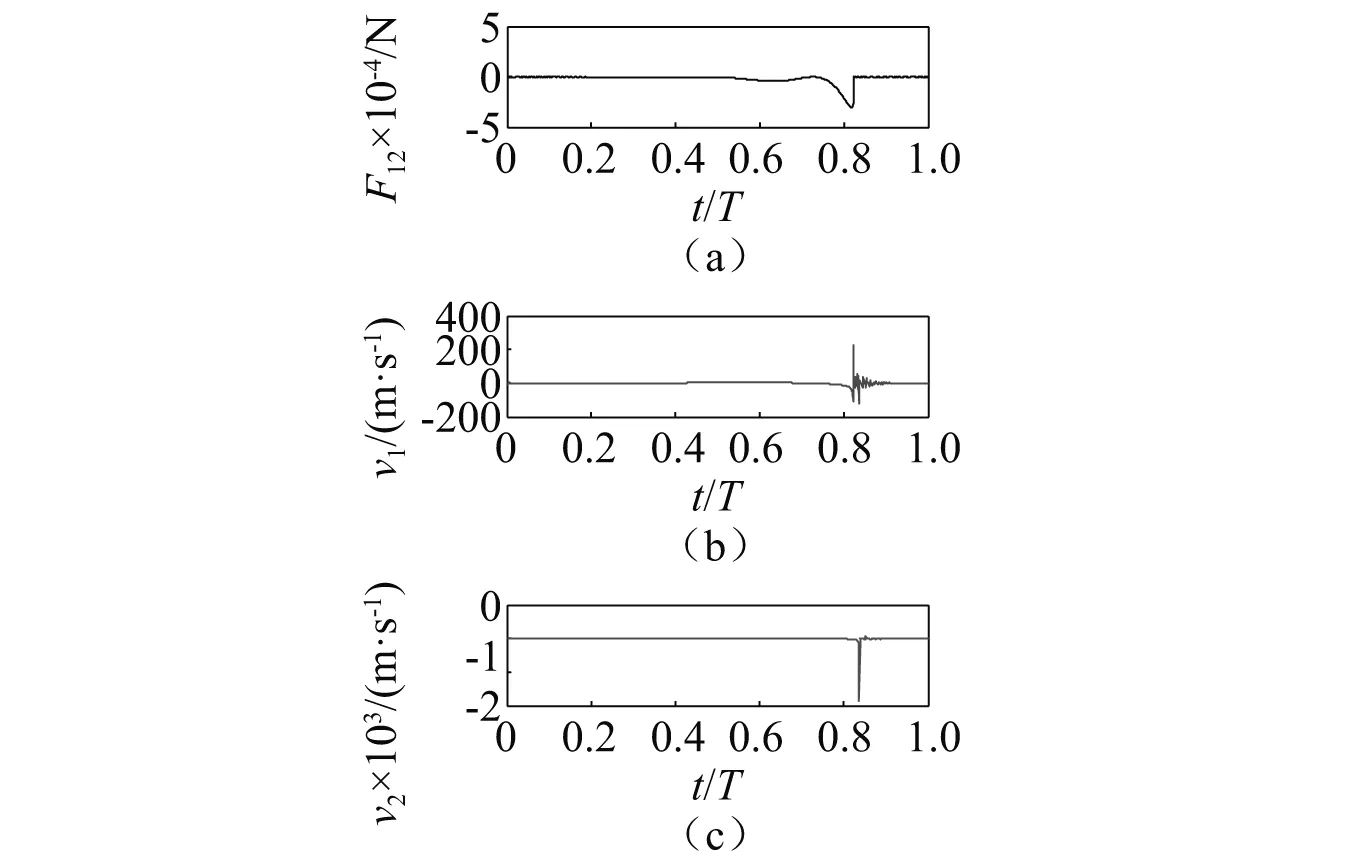
图4 驻波声场气泡之间的作用力F12和振动速度随时间的变化曲线

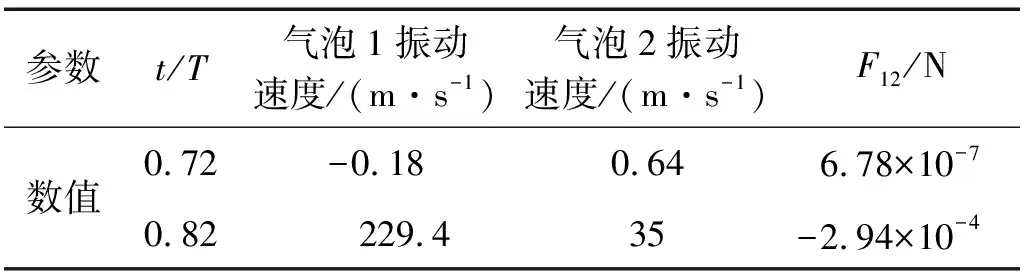
表1 驻波声场中气泡振动速度与气泡之间的作用力

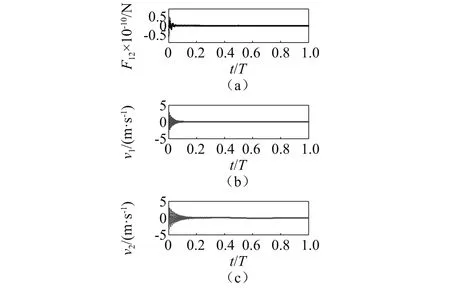
图5 平面声场中气泡之间的作用力F12、收缩速度随时间的变化曲线

在上述驱动条件下，一个驱动周期内，驻波声场中两个初始半径为2 μm和3 μm的气泡之间的次Bjerknes力为-1.56×10-5N，而平面波声场中两个初始半径为2 μm和3 μm的气泡之间的次Bjerknes力为-4.15×10-14N。对比可以发现，小振幅驱动下，平面声场中两个气泡之间的次Bjerknes力非常小，可忽略不计，而驻波声场声压波腹处两个同样尺寸的气泡之间的次Bjerknes力较平面声场中增加了几个数量级。这意味着：驻波声场波腹处两个气泡之间的次Bjerknes力不能忽略不计，次Bjerknes力使声压波腹处的大量气泡之间形成一定的稳定结构，使此处的气泡做稳态空化。

3 驻波声场波腹位置附近气泡之间次Bjerknes力及影响因素

由于驻波声场中除了距离声压波腹较近位置处气泡之间的次Bjerknes力较大外，其余位置处气泡之间的次Bjerknes力可忽略不计，见图3。因此，我们只讨论距离声压波腹较近位置处两个气泡之间的次Bjerknes力及其影响因素。

3.1 驱动压强振幅对驻波声场波腹位置附近中气泡间次Bjerknes力的影响

驱动压强振幅为0.56×105Pa，0.66×105Pa和0.76×105Pa的驻波声场中两个初始半径为2 μm和3 μm的气泡之间的瞬时作用力随时间的变化曲线，分别如图6(a)～图6(c)所示。对比图6(a)～图6(c)可知，不同驱动压强振幅下，驻波声场中两个气泡之间的瞬时作用的大小、方向随时间的变化均不相同，一个声驱动周期内的主要计算结果，如表2所示。当驱动压强振幅为0.56×105Pa时，两个气泡之间的次Bjerknes力表现为吸引力；当驱动压强振幅为0.66×105Pa时，两个气泡互相排斥；而当驱动声压振幅增加至0.76×105Pa时，两个气泡之间的次Bjerknes表现为吸引力。如果气泡之间的次Bjerknes力表现为相互吸引时，两个气泡会彼此趋近，融合为一个较大的气泡，从而使驻波声场中气泡的动力学特征发生变化，在同样的驱动声场中：一则大气泡的收缩振动幅度较小气泡而言明显减小；二则大气泡更易容易上浮，甚至上浮至液面而发生破裂。这些因素对增强空化效应是极为不利的影响。而当两个气泡之间的相互作用表现为排斥，两个气泡会彼此远离，上述模拟结果表明：驱动压强振幅能够影响驻波声场中气泡之间的相互作用力的大小、方向和空化效果。

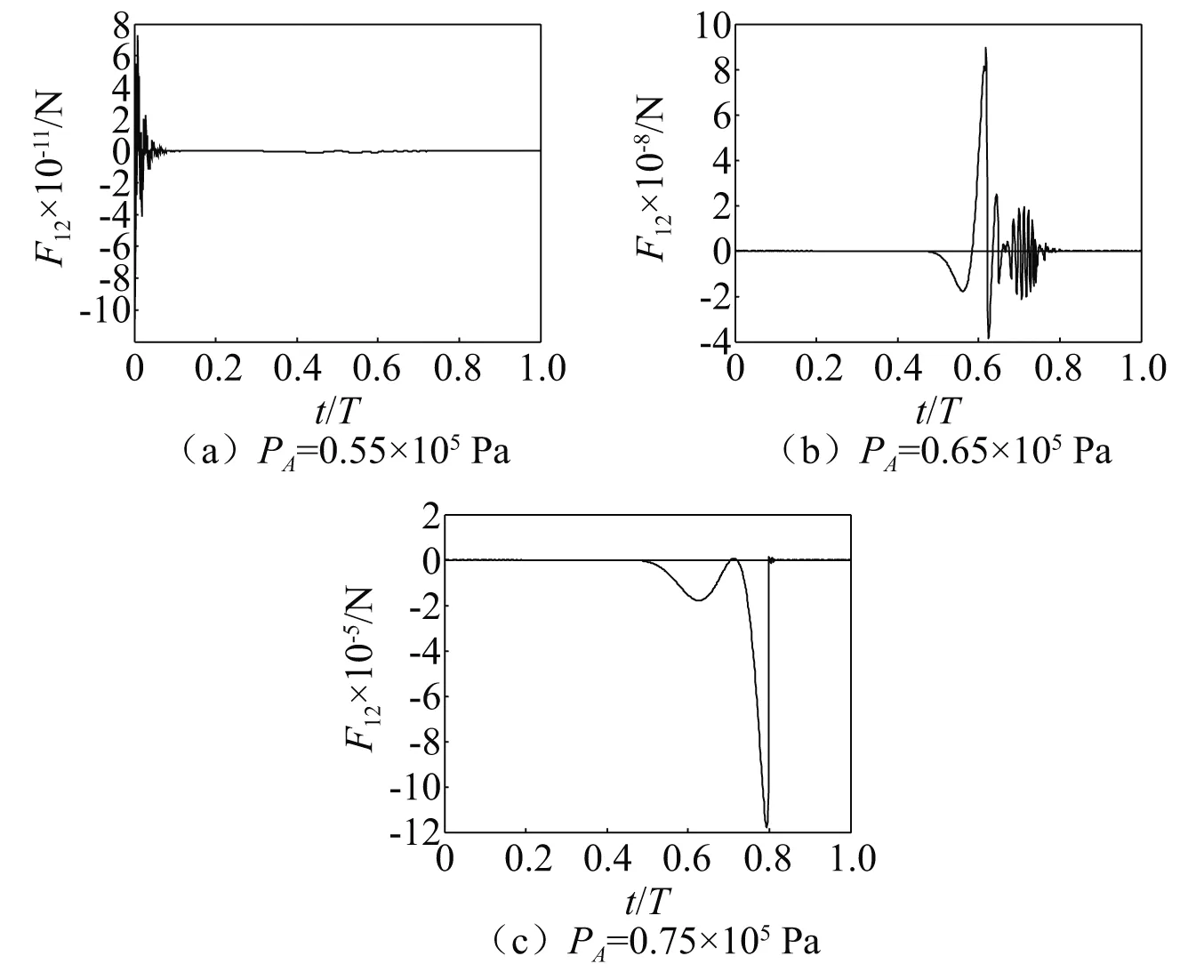
图6 两个气泡之间的瞬时作用力随时间的变化曲线

表2 不同驱动声压振幅下气泡之间的次Bjerknes力

3.2 气泡初始半径对驻波声场中波腹位置附近气泡间次Bjerknes力的影响

驱动声压振幅为0.65×105Pa，驱动频率为20 kHz的驻波声场中两个气泡之间的次Bjerknes力随气泡半径的变化情况，如图7所示。在数值模拟中我们固定气泡1 的半径为2 μm，改变气泡2的半径，数值结果表明：在上述驱动条件下，初始半径为2 μm和2.9 μm的一对气泡之间的次Bjerknes 力的大小为5.9×10-11N，为排斥力，而初始半径为2 μm和14.3 μm的一对气泡之间的次Bjerknes 力为1.17×10-11N，为吸引力。除此之外，我们注意到，当气泡1的初始半径为2 μm时，气泡2初始半径的增加会使气泡之间的次Bjerknes力出现明显的震荡，这说明气泡之间的次Bjerknes力的大小与气泡对的半径有关。综上所述：驻波声场中，当驱动声压振幅和驱动频率不变，两个气泡之间的次Bjerknes力的大小和方向均会随气泡对初始半径的变化而发生改变，气泡的初始半径是影响气泡之间次Bjerknes力的重要因素。

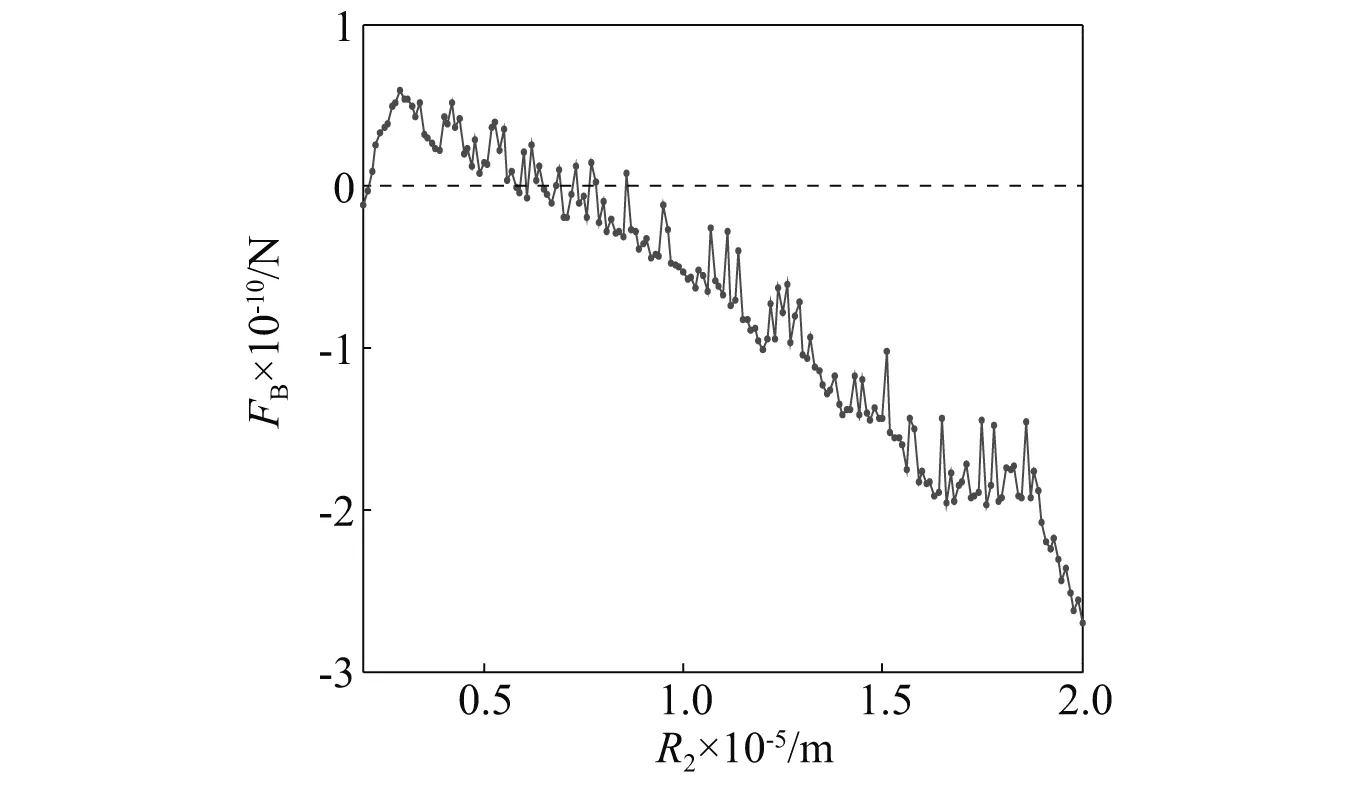
图7 次Bjerknes力随气泡半径的变化曲线

3.3 驱动频率对驻波声场中波腹位置附近两个次Bjerknes力的影响

驻波声场中两个气泡之间的次Bjerknes力和驻波声场的驱动频率也有很大的关系，驱动声压振幅为0.8×105Pa，初始半径为2 μm 和3 μm 的两个气泡之间的次Bjerknes力随时间的变化关系，如图8所示，主要计算结果如表3所示。数值模拟结果表明：在驱动声压振幅一定的驻波声场中，两个气泡之间的次Bjerknes力随驱动频率的增加而减小，在上述驱动声压振幅下，两个气泡之间的次Bjerknes力均为吸引力。上述结果表明：驻波声场中，位于波腹位置处两个气泡之间的的相互作用力在低频驻波声场中表现的更为明显，随着驱动频率的增加，两个气泡之间的相互作用迅速减小趋于0。

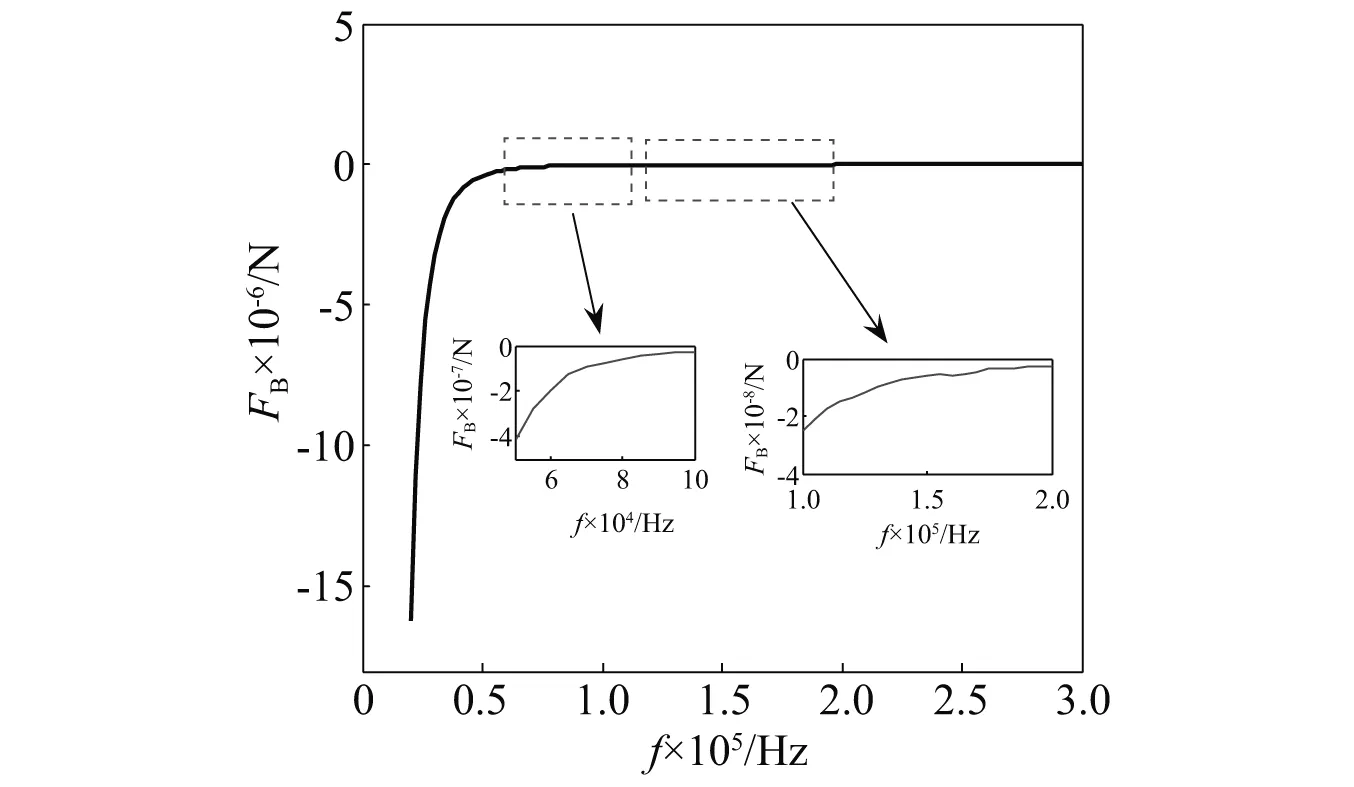
图8 次Bjerknes力随驱动频率的变化曲线

表3 不同驱动频率下两个气泡之间的次Bjerknes力

4 结 论

本文研究了驻波声场中靠近声压波腹处两个气泡的振动、能量转换及驻波声场中不同位置处两个气泡之间的次Bjerknes力特征，研究结果表明：虽然驻波声场造成了声场的不均匀性，但声压波腹位置附近，同样初始半径的气泡在驻波声场中较平面声场中具有更强的能量转换能力，驻波声场中声压波腹位置附近的小气泡能够在小振幅声压下做非线性振动，发生剧烈的空化现象，而在波节位置处只做微小的线性振动；驻波声场中小振幅驱动下两个气泡之间就具有较强的相互作用力，其中处于波腹位置处的两个气泡之间的相互作用最大，波节位置处两个气泡之间的相互作用力趋于0，可忽略不计；驻波声场中，两个气泡之间瞬时作用作用力的方向与两个气泡的振动状态有关。声压波腹位置处两个气泡之间的次Bjerknes力由驻波声场的驱动声压振幅、驱动频率和两个气泡的初始半径等因素共同决定，一对初始尺寸一定的气泡之间的相互作用会随着驱动声压振幅的增加而迅速增大，低频驻波声场中气泡之间的相互作用力明显高于高频驻波声场中气泡之间的相互作用力，低频驻波声场中，声压波腹位置处的两个尺寸相差不多的气泡之间会产生较强的吸引力，使气泡发生融合而降低空化效应。以上研究结果为超声反应器中泡群中气泡的振动、泡群结构及空化现象提供了理论基础。