转子对磁悬浮转子真空计计量特性的影响研究

2021-12-02周明旭李得天郭立新郭美如习振华邓永胜

真空与低温 2021年6期

周明旭，李得天，郭立新，郭美如，习振华，李宇，李刚，邓永胜

（1.东北大学机械工程与自动化学院，沈阳 110819；2.兰州空间技术物理研究所真空技术与物理重点实验室，兰州 730000）

0 引言

磁悬浮转子真空计（Spinning Rotor Gauge，SRG）是一种利用气体分子与悬浮在真空中自由旋转的金属球（转子）碰撞，由于切向动量传递使得转子转速衰减，而转子转速衰减率与气体压力成正比，通过对衰减率的测量实现真空压力测量的仪器[1]。该真空计内部没有电子、离子、热和辐射产生，测量时不改变气体成分和压力，吸放气现象可以忽略，无抽气效应，具有测量准确度高、线性好、重复性和长期稳定性好、结构简单等优点，可以用于单一气体和已知浓度比例的混合气体的测量。磁悬浮转子真空计具有切向动量传递系数σ稳定[2-6]；在10-4～1 Pa的压力范围中，3年内测量重复性误差小于1%[7]；除气方便（仅须150℃烘烤）等特点，一般作为传递标准对其他真空计进行校准或进行真空标准之间的比对，在真空计量[8-11]、可控热核聚变等领域得到越来越多的应用。

本文通过实验研究磁悬浮转子真空计转子的改变对测量准确度、零点稳定性的影响，确定两种不同参数的转子能否满足测量的要求，为磁悬浮转子真空计的转子选择提供依据。

1 磁悬浮转子真空计原理及实验装置

1.1 磁悬浮转子真空计原理

磁悬浮转子真空计为黏滞型真空计，其原理是通过测量由气体分子摩擦而导致的磁悬浮转子的转速衰减速率来反演真空压力的量值[12-15]。测量数学表达式如式（1）所示：

式中：d为转子直径；v为气体分子平均热速率；ρ为转子密度；α为热膨胀系数；T为温度；RD（ω）为除气体摩擦以外的转子衰减力矩；σ为宏观切向动量传递系数；ω̇/ω为减速比。

其中RD（ω）又称为残余阻尼。残余阻尼产生的主要原因是磁矩的旋转分量在测量头中产生涡流引起了损耗[16-20]，随着转子频率的增加，磁化轴和旋转轴分离，旋转分量出现。直径变动量和球形误差对转子的对称性有影响，非对称性转子会产生旋转分量，如果转子完全对称，即球形误差和直径变动量均为零，则磁化轴和悬浮轴重合，旋转分量可以忽略，残余阻尼会非常小，这样的结果有利于延伸测量下限，提高测量精度。但是，磁悬浮转子真空计正是利用旋转磁矩分量进行测量的，如果完全对称就不能测量旋转磁矩分量，无法实现真空压力的测量，因而通常选用具有一定偏心的转子。为了保证测量的准确，又能减小因为旋转磁矩分量过大而引起的涡流损耗，故采用对称性好的转子，即球形误差和直径变动量较小的转子；减速比为ω̇/ω，与压力成线性关系，因此可以在温度恒定的环境中通过测量转速比进行压力的测量。

气体压力是由转子的两个时间间隔τn、τn+1直接确定的，其对应关系如式（2）所示：

式中：τn、τn+1为两个相邻时间间隔（其中转子转动次数相同）；c0为常数。

σ是唯一要通过实验确定的参数，该参数与转子的表面粗糙度有关。球面光滑时（σ≈1），与气体的成分无关，气体分子是按照余弦定律发射的。表面粗糙时（σ>1），气体阻尼系数可由σeff估计。σeff被称之为有效切向动量传递系数，一般难以通过理论计算获得，须经过校准来确定，σeff与气—面的相互作用有关，受局部能量适应系数δ、切向动量传递系数σ以及表面粗糙度影响，可运用描述表面粗糙度的参数模型[11]进行理论估计：假设整个表面由平整表面元组成，它们倾向于一个方向，与正常表面成相同的角度θr，表面粗糙度定义为tanθr。每个倾斜的表面元贡献的一份fn(θr)代表气体分子与法向运动表面的相互作用；另一附加份额1-fn(θr)代表与切向运动表面的相互作用，两部分阻尼分别按已建立的理论进行计算。如考虑金属表面元的互相屏蔽，对沿着所有方位表面元分布各向均匀的粗糙表面，理论产生的σeff{}σ;δ与表面宏观粗糙度在下列三种情况下分别有：

在一个非常粗糙的球面上，δ相差很大的气体的σeff相对变化大约为5%，在一个光滑球面上σeff变化很小。在Ceorge等[21]的实验结果中，对于蚀刻球，各种气体的σeff最大相对变化为4.6%；对于抛光球，σeff的最大相对变化为2.6%。表面粗糙度越大σeff越大，对测量的影响越大。

为了校准磁悬浮转子真空计，研究不同表面粗糙度、直径变动量和球形误差的转子对磁悬浮转子真空计测量稳定性以及测量不确定度的影响，故将两个磁悬浮转子真空计安装在以下两套装置中进行实验比较。

1.2 气体微流量校准装置

采用气体微流量校准装置（如图1所示）进行磁悬浮转子真空计比对实验。2台磁悬浮转子真空计的物理部分（包括法兰组件和转子小球）通过金属密封的CF35法兰连接至真空室，MKS SRG-3磁悬浮转子真空计16作为参考真空计，磁悬浮转子真空计13为采用GCr15转子的实验用真空计。采用N2、Ar、He三种气体进行实验。连续烘烤抽气后，真空室内本底压力为1×10-6Pa。

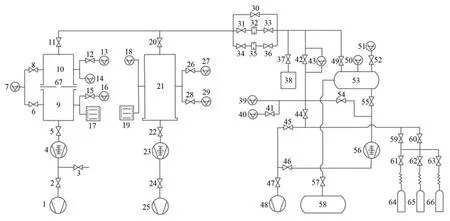
图1 气体微流量校准装置Fig.1 Gas micro-flow calibration apparatus

1.3 静态膨胀法真空校准装置

采用静态膨胀法真空校准装置对磁悬浮转子真空计进行校准实验。静态膨胀法真空校准装置主要由前级压力测量系统、压力衰减系统、抽气系统和烘烤系统四部分组成，其工作原理如图2所示[22]。图中6为MKS SRG-3型磁悬浮转子真空计，8为更换了GCr15转子的磁悬浮转子真空计。前级压力由DPG8 Ⅱ型数字式活塞压力计测量，其不确定度为0.005%。压力衰减系统由取样室和校准室组成。抽气系统由机械泵、双级涡轮分子泵串联组成。装置的本底压力为3.17×10-8Pa。

图2 静态膨胀法真空校准装置Fig.2 Static expansion vacuum standard apparatus

2 实验测试及数据分析

2.1 不同气体介质中实验测试

实验分别采用N2、Ar、He三种气体对MKS SRG-3和更换为GCr15转子的2台磁悬浮转子真空计进行测试。实验前，装置抽至本底压力，随后充气改变测试压力，压力为10-4～1 Pa，每个量级分别选取1个压力测试点，待稳定后连续测量八组，每组测量时间间隔为2 min。实验中保持实验室内环境温度为23℃±1℃。每次拆装磁悬浮转子真空计时，要保证转子真空计的法兰为水平，以保证测量信号的准确性。测量前要保证磁悬浮转子真空计运转至少3 h以上，以提高真空计的测量准确性[15]。由于磁悬浮转子真空计的转子略有偏心，而转子每次悬浮时其方向是随机的，转子悬浮后磁矩旋转分量的大小都会发生变化，故残余阻尼也会发生变化，因而要在每次测量压力前重新确定残余阻尼，作为本次测量的修正值，这对于测量的准确性十分必要[1]。用图1中的磁悬浮转子真空计13和16记录零点读数，13的转子为GCr15材料、直径变动量为0.25µm、球形误差为0.25µm、表面粗糙度为0.020µm。

在Ar中，2台真空计在不同量级下压力示值的比值如图3所示，比值分布均在0.970附近，随着压力升高，趋于稳定。

图3 Ar中不同量级下压力示值比值Fig.3 Ratio of values at different orders of magnitude in Ar（MKS SRG-3/GCr15 rotor）

在He中的测量结果如图4所示，与在Ar中的测试结果相似。在10-4Pa量级，测量数值波动最大，随着压力升高，测量波动逐渐减小。在10-4Pa和10-3Pa量级下，数据波动较在Ar中显著，在10-3Pa量级，测量结果与均值的最大偏差为在Ar中的10倍。不同量级下的比值均在0.963上下波动。在N2中，不同量级下的比值均在0.976上下波动，如图5所示。

图4 He中不同量级下压力示值比值Fig.4 Ratio of values at different orders of magnitude in He（MKS SRG-3/GCr15 rotor）

图5 样本一在N2中不同量级下压力示值比值Fig.5 Ratio of values at different orders of magnitude of sample one in N2（MKS SRG-3/GCr15 rotor）

每个量级的采样数据个数n=8，使用极差法评定GCr15转子真空计的A类标准不确定度，得到每个量级的不确定度。

式中：R为极差；xmax为测量结果最大值；xmin为测量结果最小值；s（x）为实验标准偏差；n为采样数据个数；C为与n有关的无偏差极差系数，查表得C=2.85；u(x)为测量不确定度。

整体范围采样数据n=32，使用贝塞尔式（4）评定A类标准不确定度，得到测量不确定度。

式中：xi为第i次测量的结果；xˉ为n次测量结果的算数平均值；u(x)为测量不确定度。表1为不同气体下的不确定度。

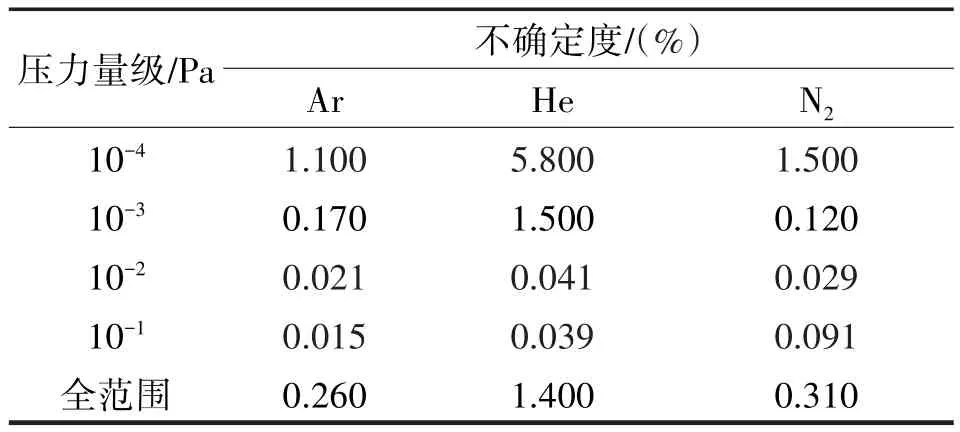
表1 GCr15转子真空计不同气体下测量结果的不确定度Tab.1 Uncertainty of measurement results of GCr15 rotor vacuum gauge under different gases

通过以上实验可以得出，磁悬浮转子真空计在Ar和N2环境中的测试数据比在He中的稳定，由图3看出，在Ar中具有最高的零点稳定性。在不同的气体中，GCr15转子磁悬浮转子真空计在10-4Pa量级下的波动较为明显，随之压力升高波动降低。每组实验前，磁悬浮转子真空计均已运转3 h以上，温度达到平衡，涡流对转子加热的影响已经排除，因此，产生上述波动的主要原因是零点的漂移。采用GCr15转子的磁悬浮转子真空计测量不确定度均小于1.5%，在Ar中能够达到0.26%。

2.2 不同转子真空计的实验测试

采用N2在气体微流量校准装置上进行实验，转子材质均为GCr15，直径4.5 mm，样本一、样本二、样本三的转子直径变动量0.25µm，球形误差0.25µm，表面粗糙度0.020µm；样本四的转子直径变动量0.13µm，球形误差0.13µm，表面粗糙度0.014µm。比对真空计为MKS SRG-3。

在N2环境中进行压力范围的测量，四个样本的测量数据分别如图5、图6、图7和图8所示。

图6 样本二不同量级示值比值Fig.6 Ratio of values at different orders of magnitude of sample two（MKS SRG-3/GCr15 rotor）

图7 样本三不同量级示值比值Fig.7 Ratio of values at different orders of magnitude of sample three（MKS SRG-3/GCr15 rotor）

图8 样本四不同量级压力示值比值Fig.8 Ratio of values at different orders of magnitude of sample four（MKS SRG-3/GCr15 rotor）

样本二在10-4Pa量级的测量数值波动较大，随着压力的升高，波动逐渐减小。MKS SRG-3与样本二示值的比值稳定在1.000附近。样本二在10-4Pa量级的测量数值波动最大，随着压力升高波动逐渐减小，但波动程度不同，可归因于转子的个体参数差异，不同量级下的比值均在0.985附近。MKS SRG-3与样本四测量结果的比值约等于1.000，且上下浮动不超过3%，表明转子几何和表面参数精度的提高有助于提高测量准确性。

不同转子对应的测量结果的不确定度如表2所列，样本四测量结果的不确定度优于样本一和样本二，表明具有较小直径变动量、球形误差和表面粗糙度的转子有助于减小残余阻尼、降低测量数据的分散性。

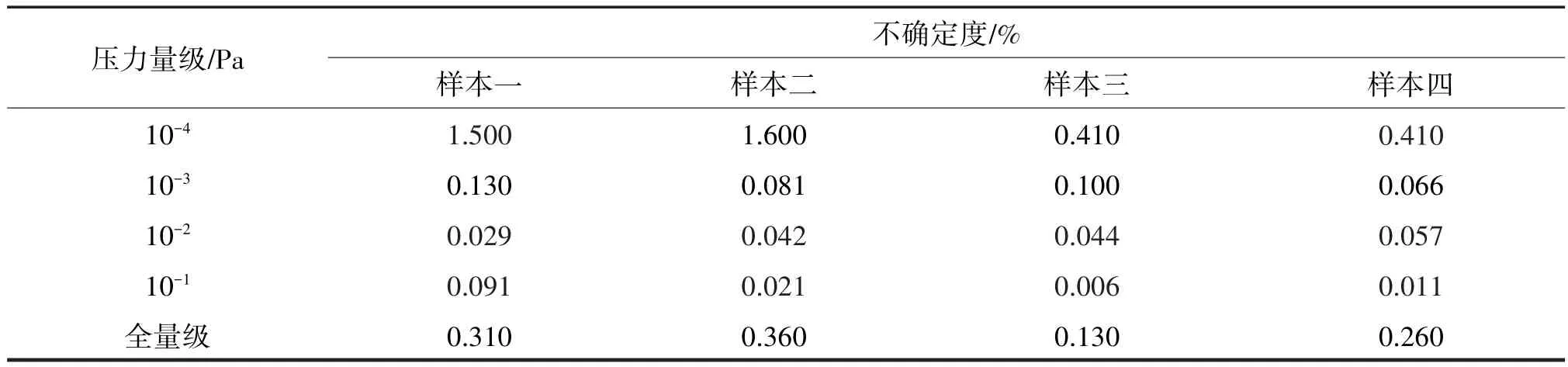
表2 不同转子真空计对应测量结果的不确定度Tab.2 Uncertainty of measurement results for different rotors

2.3 不同转子真空计的零点稳定性实验测试

在实验装置本底压力下，测试各样本对应的零点稳定性，每个样本分别测试6次，实验数据如表3～6所列。从表中可以看出，样本一、二、三相应的零点波动明显大于样本四。四个样本的零点波动均与MKS SRG-3接近。样本四的零点波动比样本一、二和样本三小一个数量级，这有利于进一步扩展磁悬浮转子真空计的测量下限。

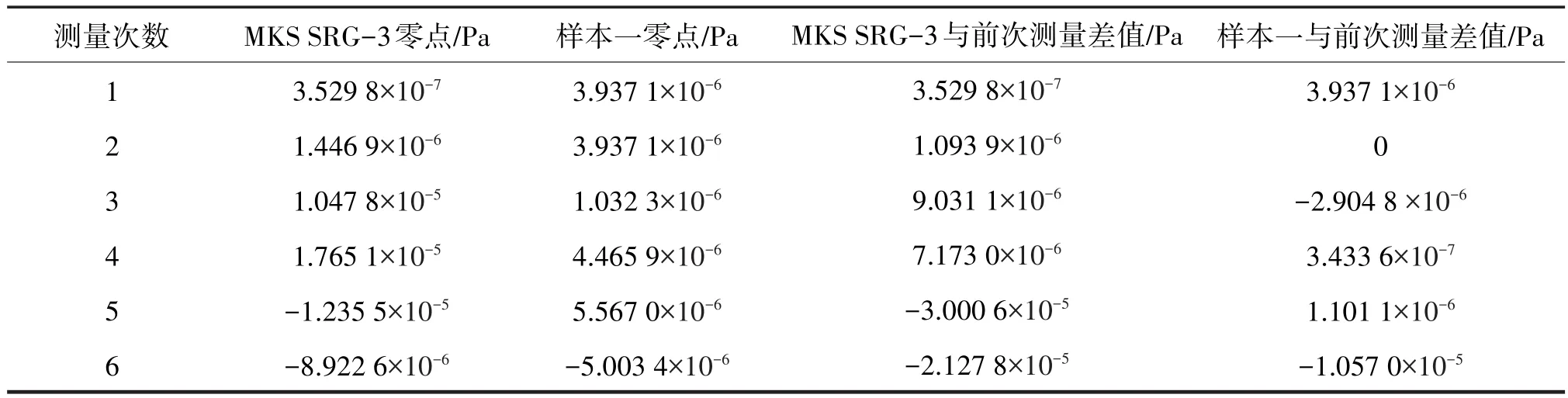
表3 样本一零点波动Tab.3 Sample one zero-point fluctuation

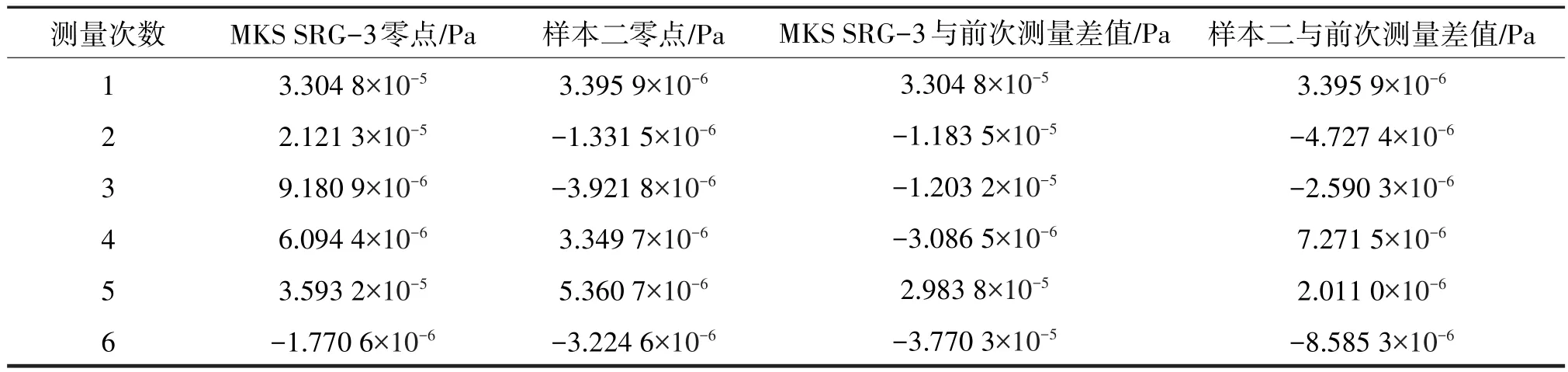
表4 样本二零点波动Tab.4 Sample two zero-point fluctuation

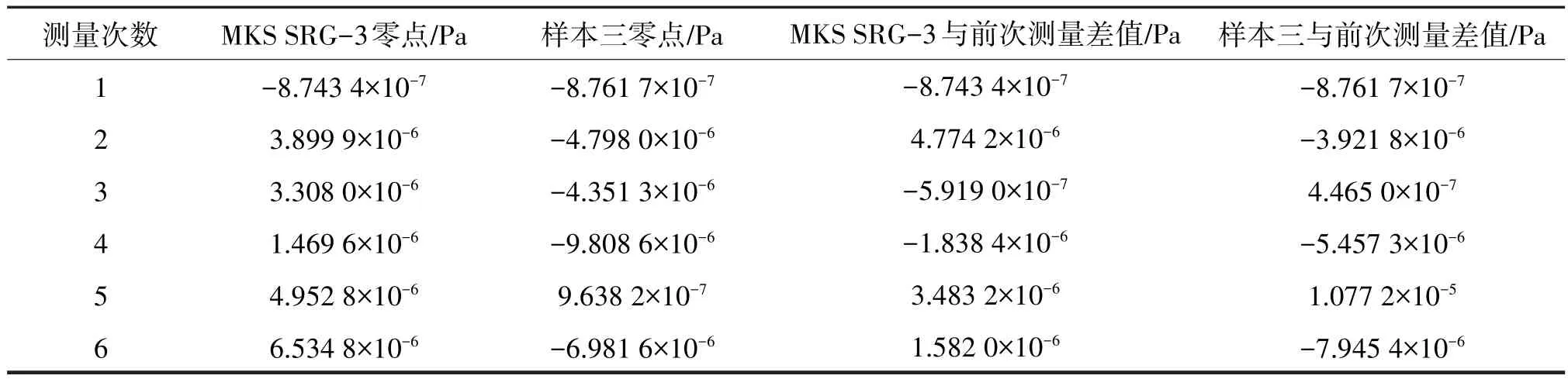
表5 样本三零点波动Tab.5 Sample three zero-point fluctuation

表6 样本四零点波动Tab.6 Sample four zero-point fluctuation

2.4 静态膨胀法真空校准实验

通过上述实验可知，样本四具有良好的测试结果。为进一步验证测量结果的准确性，采用静态膨胀法真空校准装置对样本四进行校准，并与MKS SRG-3的校准结果进行对比。

将不同转子的两个磁悬浮转子真空计（样本四和MKS SRG-3）安装在左校准室上，如图2中6、8所示。通过一级膨胀，获得10-1Pa和10-2Pa量级的标准压力；在一级膨胀的基础上进行二级膨胀，获得10-3Pa、10-4Pa量级标准压力，同时记录两个真空计的压力示值。表7、表8分别为第一次和第二次测量结果。