微米尺度不锈钢丝网填料阻力特性研究
2021-12-02商丹枫崔晓钰陈志超蒋珍华刘少帅吴亦农
商丹枫,崔晓钰 ,陈志超,蒋珍华,刘少帅,吴亦农
(1.上海理工大学,上海 200093;2.中国科学院上海技术物理研究所,上海 200082)
0 引言
金属多孔介质分为烧结金属粉末多孔介质和金属丝网填料多孔介质,后者常用于热交换、过滤与分离等场合。不锈钢丝网是比较常见的多孔介质材料[1],具有高导热性能,材料廉价,易于制造等优点,按孔径大小可分为微米尺度(1~100µm)和宏观尺度(大于1 mm)。宏观尺度的丝网常常用于过滤与分离,微米尺度丝网用于热交换较多。多孔介质内部流体的流动与换热[2-4]一直是一个研究热点。多孔介质区域流道复杂多变,流体流动状态用数学公式难以准确描述,传热规律也难以用准确的关联式表示,数值仿真计算是一种研究丝网多孔介质流动与换热的有效方法。
确定多孔介质阻力参数的方法主要有两种[5-6]。一种是使用计算流体动力学(CFD)技术创建多孔介质微观模型,确定压降特性,该方法依赖于理想化的多孔介质结构;第二种方法是通过实验获得多孔介质压降,再由此计算出阻力参数。Harvey[7]建立了一维多孔介质模型并实验确定了325目和400目丝网阻力参数。胡伟[8]基于CFD仿真软件研究了流体速度和丝网结构对丝网多孔介质流体压降的影响规律。温永刚等[9]用有限元分析软件对多孔介质整体温度场分布进行数值模拟,并实验验证了模拟结果。侯宗宗等[10]通过数值仿真获得金属滤网性能曲线,并通过实验验证得到高可靠性数值模型。王俊涛等[11]基于FLUENT对多孔介质的传热及阻力特性进行了模拟研究,发现当速度一定时,传热效率随孔隙率增大而增加。王晓倩等[12]从理论、实验和数值模拟三个方面对多孔介质内流动与换热研究进展作了详细论述。金属丝网作为斯特林制冷机回热器填料,对传热和压降的影响是决定能源效率的主要因素,许多研究人员对此开展了深入的研究[13-14]。金属丝网在回热器中起到存储和释放热量的作用,制冷机填料最常使用的是丝径18~32µm、目数353~552、孔径28~40µm的不锈钢丝网[15]。微米级丝网尺度既能满足换热需求,压降也在可控范围内,孔径过大影响换热,孔径过小压降较大。赖华盛[16]等对斯特林制冷机回热器传热能力进行仿真计算,拟合出较为可靠的传热关联式。高凡等[1]模拟不同丝径、目数,不同材料的回热器丝网,进一步优化了回热器传热性能;控制不同目数丝网填充比例,以提高回热器效率。Clearman等[17]实验测量了脉管回热器的压降,基于FLUENT软件建立了脉管回热器多孔介质模型。陈曦等[18]采用FLUENT软件对低温制冷机中填充的多孔介质进行了数值分析,研究了孔隙率和流体入口速度对流动和换热的影响,得到压降与换热效果的最优比值。隆瑞等[19]用数值计算方法研究了层流状况下微通道内不同目数金属丝网的传热与流动特性,发现100目时,流动阻力较小,换热效果最好。目前,许多学者基于数值仿真的方法对多孔介质的流阻特性进行了研究,建立了一些代表性的关联式,但实验值与模拟值存在偏差,关联式并不适用于其他研究者的多孔介质模型。
为探究阻力损失特性,本文将从影响流阻的关键参数出发,运用数值模拟以及实验验证的方法,建立以不锈钢丝网为填料的多孔介质数值模型,给出丝网多孔介质孔隙率、黏性阻力因子和惯性阻力因子的计算方法,为后续研究提供一定参考。
1 模型参数
1.1 物理模型
为计算通过丝网的流体压降,设计了一套实验装置,材料为不锈钢,结构如图1(a)所示。同时建立了三维仿真计算流体域物理模型,包括入口、出口、圆形流道、渐扩口和丝网填充段。入口流道直径2 mm,长12.9 mm,丝网段直径8 mm,长0.2 mm,出口段直径2 mm,长11.9 mm,总长度26 mm。不锈钢丝网为500目,丝径23µm,丝网填料段由多片丝网堆叠,工质为氦气,氦气沿轴向通过丝网填充段从另一端流出,如图1(b)所示。
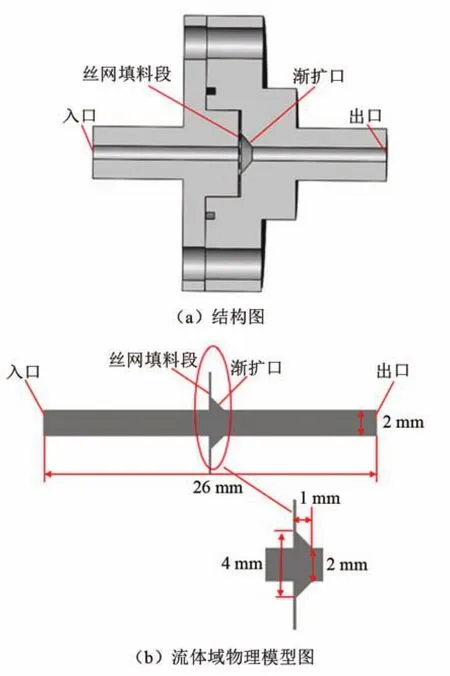
图1 丝网填料实验装置及流体域物理模型图Fig.1 Experimental device of wire mesh packing and physical model of fluid domain
图2为丝网示意图,整片丝网直径为8 mm。在数值仿真过程中,为简化模型,对丝网作出以下假设:
(1)丝网的结构形状,排列方式一致;

图2 不锈钢丝网照片Fig.2 Woven wire mesh and magnified image of microscope
(2)丝网多孔介质中单片丝网之间不发生相对位移。
1.2 边界条件和控制方程
边界条件设置为:速度入口边界条件、压力出口边界条件、固体壁面无滑移边界条件和固体壁面绝热边界条件。对于多孔介质模型,在数值计算中,将多孔区域设置为流体类型,最重要的是确定孔隙率、黏性阻力因子和惯性阻力因子。多孔介质模型[15]是在动量方程上加入一个动量源,动量源与速度相关。多孔介质守恒方程包括质量守恒方程和动量守恒方程:
质量守恒:
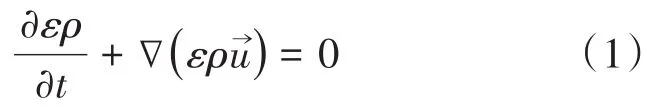
动量守恒:
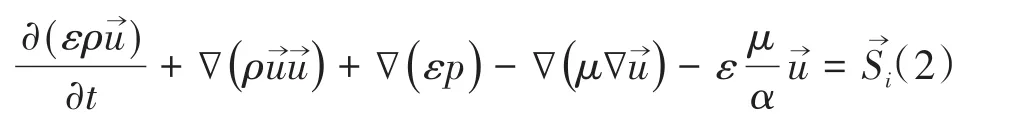
其中:

式中:Si为第i个(i为x、y或z方向)动量源项;ε为孔隙率;α表示渗透率;τ为剪切力;D为黏性阻力因子;C为惯性阻力因子;μ为动力黏度;u为速度;ρ为密度;t为时间;j为x、y、或z方向的分量;p为流体压力。
假设流体只在轴向上有速度梯度,其他方向速度梯度为零,公式可以简化为:

式中:1/α=D;将公式进一步简化可得到多孔介质压降与速度的关系,阻力源项与多孔区域厚度∆n的乘积Δp为压降:
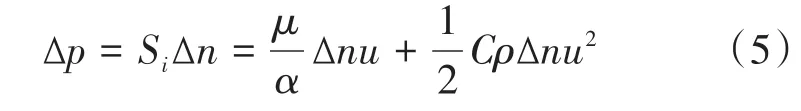
压力损失受一些主要参数,如流体速度、流体物性和多孔介质材料特性等的影响。流体速度主要由流体质量流量和流体物性决定,流体物性由温度和工作压力决定,多孔介质的材料特性决定孔隙率、惯性系数和黏性系数。Ergun[20]认为多孔介质内部的压降是黏性能量损失和惯性能量损失的和,并且推导出统一的方程,此方程适用于所有类型的流动,称之为Ergun方程:
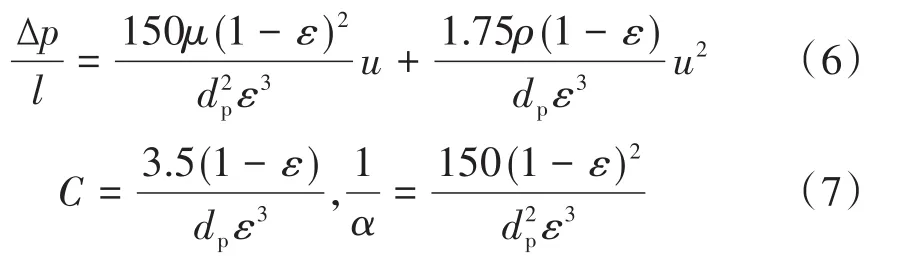
式中:l为多孔介质的厚度;dp为多孔介质的孔径。
Ergun通过实验测得惯性和黏性修正系数分别为150和3.5,通过多孔介质进出口压降和通道流速,可以拟合一个压降关于速度的二次方程,对比厄根方程可得出孔隙率与孔径。若流动为层流,则不考虑惯性项。流体在管内的流动状态分为层流和湍流,Re小于2 300为层流,Re大于10 000为湍流,2 300≤Re≤10 000为过渡区[19]。

式中:G为质量流量;ν为运动黏度;d为圆管内径。
当氦气工质压力为1.7 MPa,温度为293 K时,氦气密度为 2.8 kg/m3,运动黏度为 7.1×10-6m2/s。在多孔介质区域,流道直径8 mm,当氦气质量流量为18.2 mg/s时,由式(8)计算得Re为147.4,小于2 300,此时氦气工质流动状态为层流。
丝网多孔介质和颗粒多孔介质存在较大区别,丝网材料比较均匀,一般认为是各向同性材料,其多孔区域由多片丝网堆叠组成,丝网多孔材料的孔隙率由丝网丝径和目数决定,假设丝网表面没有卷面和变形,可由以下公式[21]得到黏性阻力因子、惯性阻力因子和孔隙率[22-23]:

式中:m为丝网丝与丝之间的距离;β为多孔介质中横截面上流通面积与横截面的面积比;z为丝网目数;n为单位长度上丝网的数量;dw为丝网丝径。给定丝网,就确定了多孔介质守恒方程中的参数。
1.3 网格无关性检验
为保证计算结果的准确性,对计算模型进行网格无关性验证,选择质量流量为11.1 mg/s、15.2 mg/s、18.2 mg/s和比较大的网格数量变化范围,即10万、24万、82万、143万和238万进行验证,如图3所示。可以看出,随着网格数量增大,压降发生明显变化。网格数为82万时出现拐点;当网格数量小于82万时,无法获取准确压降值;网格数量超过82万后,随着网格数量增大,压降几乎无变化,只是增加了计算时间,对计算结果的准确性无贡献,故选择网格数量82万进行仿真计算。
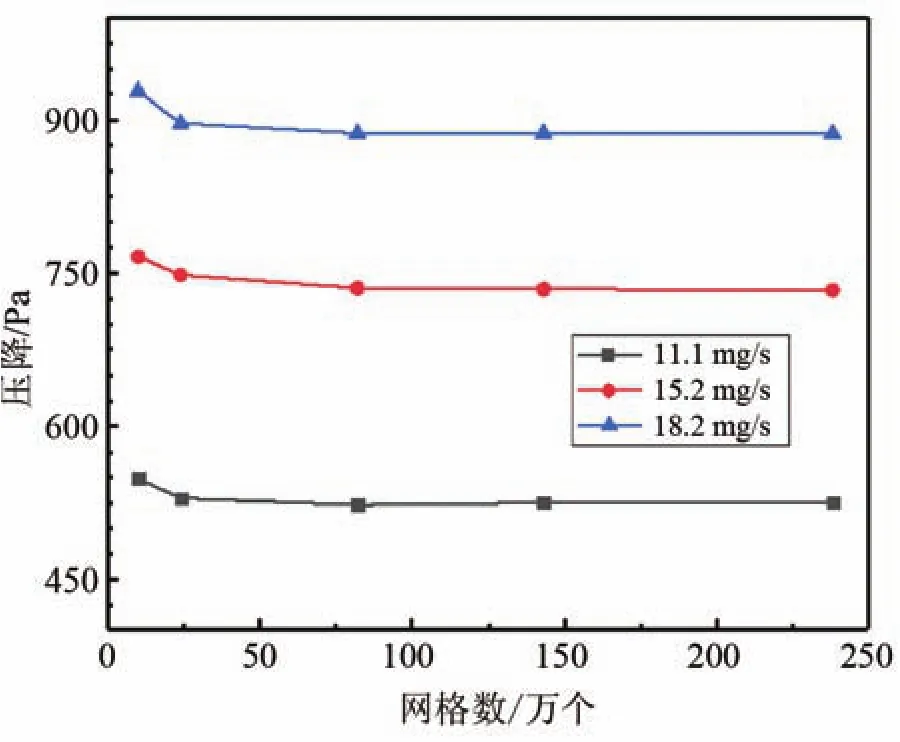
图3 网格无关性检验Fig.3 Grid independence test
1.4 模型验证
压降测试实验流程如图4所示,由氦气瓶提供的高压氦气经过调节阀后,通过旋拧阀注入实验系统,调节旋拧阀控制工作压力大小,调节针阀控制质量流量大小。配合使用旋拧阀和针阀,探究给定工作压力下不同质量流量的丝网压降。

图4 压降测试实验流程图Fig.4 Schematic diagram of the experimental process
如图5所示,当工作压力为1.7 MPa时,在0~18.2 mg/s内,随着流体质量流量增大,压降增大,模拟数据与实验值吻合良好,误差小于5%;由图可知,无论是模拟值还是实验值,压降与流体质量流量均成正比关系,多孔介质压力损失由黏性力和惯性力共同决定,流体状态为层流时,只有黏性力起作用,此时压降为黏性力与流体速度的乘积,与流体质量流量成正比。
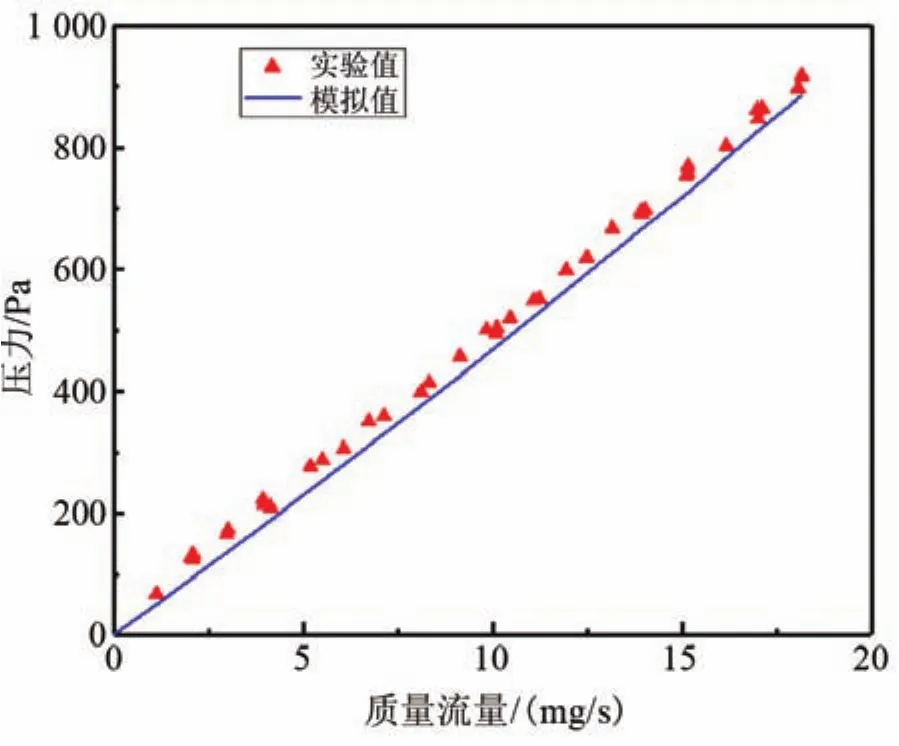
图5 多孔介质区域压降与质量流量的关系Fig.5 Relationship between pressure drop and mass flow rate in porous media area
丝网多孔介质流阻模拟数据与国内外学者的经验公式对比关系如图6所示。选用本文中丝网多孔介质的参数尺寸,分别用不同学者的经验公式计算出流阻数据,流体速度为0~1 m·s-1,对比压降与流经丝网多孔介质流体速度的关系。胡伟[8]、侯宗宗等[24]和Koiodziej等[25]三者经验公式的压降预测值与本文模拟数值偏差较大,三者的压降与速度不成正比关系。Wu等[26]的研究结果与本文模拟值趋势一致,压降与速度基本成正比关系,但也存在一定偏差。本文模拟值与实验值基本一致,与其他学者的经验关联式的对比表明,本文模型较为可靠,能够较为准确地预测实验值。
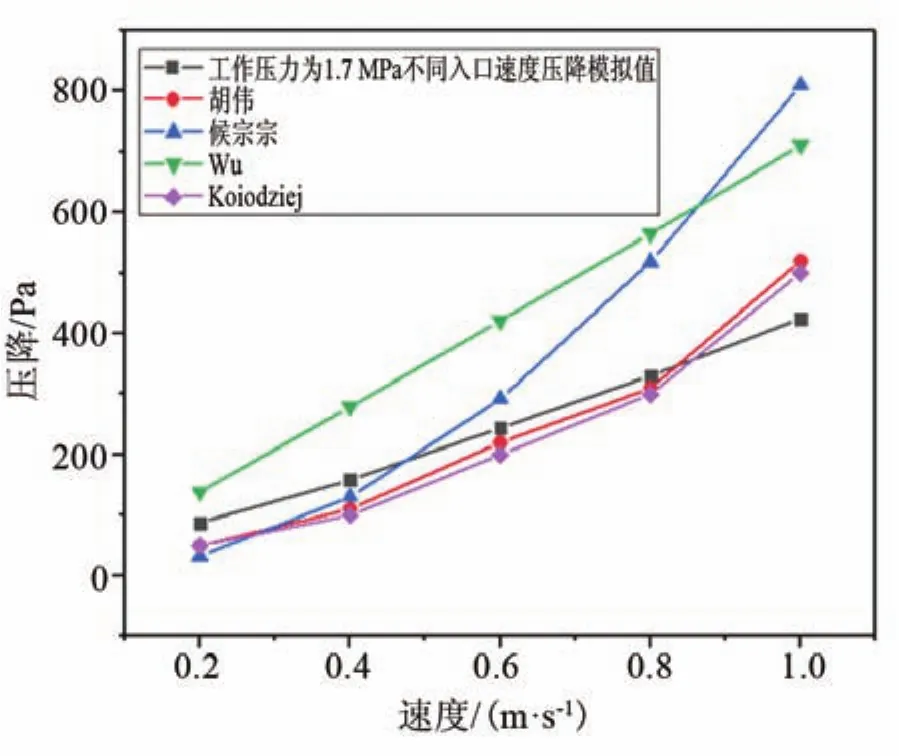
图6 丝网多孔介质流阻模拟数据与经验公式对比Fig.6 Comparison between simulation data and empirical formula of flow resistance in mesh porous media
1.5 不确定度分析
将质量流量计、压力传感器和差压计直接安装在测试回路中,测量误差主要来自测量精度。表1列出了实验用测量仪器的参数。

表1 测量仪器量程及精度Tab.1 Sensor range and precision
2 结果与讨论
2.1 流量对压降的影响
将模型划分为80万网格进行仿真计算。工作压力为1.7 MPa,质量流量分别为11.1 mg/s、15.2 mg/s和18.2 mg/s的流体沿轴向的压力变化如图7所示。为更加清晰地表示流体压力变化,引入过余压力pp=1.7 MPa+Δp,Δp为压降(图7描述的压力为过余压力)。流体通过丝网前产生一个高压区域,通过丝网填充段后产生一个低压区域,在丝网多孔段中心区域,压力沿着流动方向均匀降低;不同质量流量时,流体压力分布趋势相同,反映了流体经过丝网填料时的变化过程,与理论模型较为一致;在1.7 MPa的工作压力下,随着质量流量的增大,压降增大。

图7 不同质量流量的轴向压力分布Fig.7 Axial pressure distribution of different mass flow
2.2 丝网对压降的影响
如图8所示,取平行于轴向的截面作为研究对象。未填充丝网时,轴向压力呈较为均匀的梯度变化,在径向上,除去中间直径突变段,其他部分压力梯度随着流体运动呈逐渐增大趋势,由于中间变径段厚度较小,即使未填充丝网,流体仍然未扩散到远端;当变径段填充丝网后,可以看出,压力在该截面上分为三个不同区域,丝网填料中为压力突变区域,从入口段到进入丝网填料前,压力梯度较小;在丝网填料段,由于流体进入丝网时,流道直径突然从2 mm扩大到8 mm,丝网填料段又比较薄,只有0.2 mm,因此径向上流体阻力损失较大,流体无法扩散到远端,只通过中心区域,径向远端认为是没有流体通过的状态;从流体通过丝网填料段后到出口段,压力几乎无变化。

图8 有无丝网填料的截面压力云图Fig.8 Cross-sectional pressure cloud diagram with or with‐out wire mesh packing
取轴向上中心轴线作为监控对象,在图9所示的未填充丝网模型中,入口处压力呈增大的趋势,随后压力逐渐降低,进出口平均压降为3 Pa;在图9填充丝网模型中,填充丝网段流体压力陡然下降,进出口平均压降为750 Pa;在中间变径段,压力从750 Pa降至10 Pa以内。
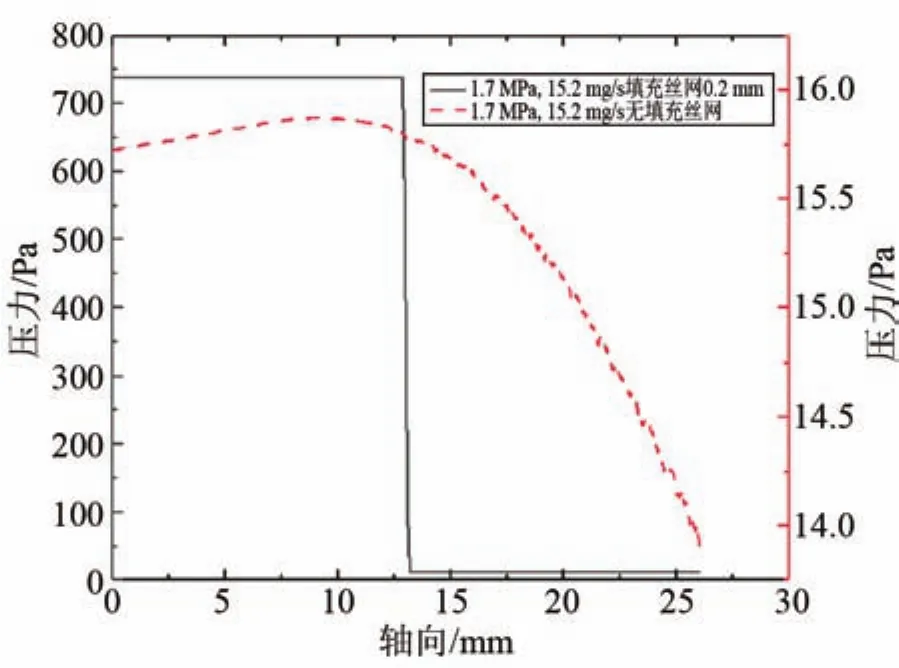
图9 轴向流动中轴线流体压力分布Fig.9 Pressure distribution on the central axis in the mainstream direction
图10为流体在中轴线的速度分布。沿流动方向流体速度逐渐增大,模型设置为速度入口,入口处速度表示入口截面平均速度,轴向其他位置只表示该处速度。在无填充丝网模型中,中间段管道直径变大,流体速度下降;填充丝网后,流体进入丝网段,速度骤降,流体通过丝网后速度逐渐增大。

图10 轴向流动中轴线上流体速度分布Fig.10 Axis velocity distribution in the mainstream direction
当入口速度给定为1.7 m·s-1,工作压力为1.7 MPa时,改变丝网填料段厚度,计算压力分布。如图11所示,随着丝网填料段厚度增加,未填充丝网和填充丝网时压降均增大,有丝网填料时压降变化较大,丝网填料段增厚使填充丝网厚度增加,阻力损失显著增大。

图11 压降与丝网填料厚度关系Fig.11 Relationship between pressure drop and screen thickness
2.3 导流效应对流动状态的影响
渐扩口对流体有一定导流作用,为验证渐扩口导流效果,改变流体流动方向,在1.7 MPa、15.2 mg/s的工况下仿真计算。如图12所示,流体中间变径段压力分布与未改变流动方向时相比无明显变化,平均压降相差20 Pa。

图12 不同流动方向的压力云图Fig.12 Pressure cloud diagrams in different flow directions
图13为不同渐扩口开度的流体速度云图。渐扩口没有改变流体运动状态,随着渐扩口开度变大,流体径向无明显扩散,进出口平均速度变化较小,蓝色区域没有流体通过,渐扩口的导流影响有限。

图13 不同渐扩口开度的流体速度云图Fig.13 Velocity cloud diagram of diversion diversion at different openings
3 结论
通过对丝网多孔介质模型的仿真计算,得到不同工况下流体流过丝网的流动状态,经分析得出以下结论:
(1)压降与流体速度成正比关系,实验值与模拟值吻合良好,误差为5%,多孔介质丝网模型计算较为准确。
(2)对于多孔丝网模型,轴向流动时流体经过丝网产生的压降与轴向位置近似成正比关系,压力和速度在丝网段骤降,阻力明显增大,流体阻力损失主要在丝网填充段。
(3)对于向不同方向流动的流体,渐扩口几乎无导流作用,流体压力和速度分布无明显变化;随着丝网填料厚度增加,阻力损失显著增大。
