长航时飞行器多元件随机失效模型与损伤评估
2021-12-02白树伟童明波常文魁
白树伟 姜 楠 童明波 常文魁
1.上海机电工程研究所,上海,201109 2.上海航天电子技术研究所,上海,201109 3.南京航空航天大学航空学院,南京,2100164.中国飞机强度研究所,西安,710065
0 引言
随着断裂力学的发展和损伤容限分析技术的完善,裂纹扩展分析及剩余强度评估已被广泛应用到飞机设计和维护中,以保障飞机服役期间的结构完整性。然而,由于飞机服役年限的进一步提升,广布疲劳损伤(widespread fatigue damage,WFD)造成了结构失效。针对WFD的评估,采用现行的损伤容限评定方法通常只限制主裂纹的临界裂纹长度,并没有考虑到多裂纹间的相互作用。事实上,随着结构多处裂纹的萌生扩展,这些裂纹相互影响,尤其是在裂纹扩展后期会产生强烈的干涉而导致应力强度因子明显增大,加速裂纹扩展,使裂纹扩展寿命变短,因此,需要针对结构的WFD进行整体评估。
目前,国内外各航空研究院所及科研院校对WFD评定技术及方法进行了研究[1-7],这些研究通过变量的随机性描述裂纹萌生、扩展过程中的不确定性, 建立WFD失效过程的概率模型,且研究对象多集中于多部位损伤[1-4],关于多元件损伤的报道较少。作为WFD的两类主要损伤源,多部位损伤与多元件损伤的主要区别在于裂纹间的相互影响程度。多部位损伤结构的裂纹间距较近,裂纹间相互作用更强;多元件损伤裂纹尖端相距较远,裂纹间的相互作用并不显著。管世民等[8]将多元件损伤简化为结构局部刚度下降导致的载荷再分配问题处理。
针对多元件损伤研究较少、简化过程忽略失效过程随机性等情况,本文建立了随机失效模型,研究多元件损伤概率评估方法。以国内外试验数据为主要来源,通过五隔框机身算例验证评估方法的有效性,并依据七隔框机身疲劳试验结果进行多元件评估,给出结构检查修理时刻。
1 广布疲劳损伤平均行为
对WFD敏感结构的判别往往遵循结构相似原则、结构相似细节大区域判断原则、应力相似原则和疲劳寿命相近原则,其中,多元件损伤的特征在于相似的元件存在多个裂纹,这些裂纹在相似的应力下扩展或具有相似的疲劳特性。当结构元件具有不超过10%的应力差异时可被视为“在相似应力下运行”,即细节的最大应力水平在以平均应力值为中心的10%带宽内可认为结构细节应力相近。当结构细节构型和几何尺寸有差异时,可通过计算出结构细节疲劳额定值(detailed fatigue rating,DFR)进行定量的判断,如果结构细节的DFR值在以平均DFR值为中心的10%带宽内,则可认为结构细节相似。
对于WFD敏感结构区域,关键问题是确定广布疲劳损伤平均行为时刻Nave。由于广布疲劳损伤失效时间与材料工艺水平、结构装配方法、使用环境载荷等密切相关,多种因素的随机性叠加使广布疲劳损伤发生时刻具有一定的分散性[9-11],通常将不加干预的情况下机队中50%的飞机发生WFD的时间点作为广布疲劳损伤平均行为时刻,其定义如图1所示。
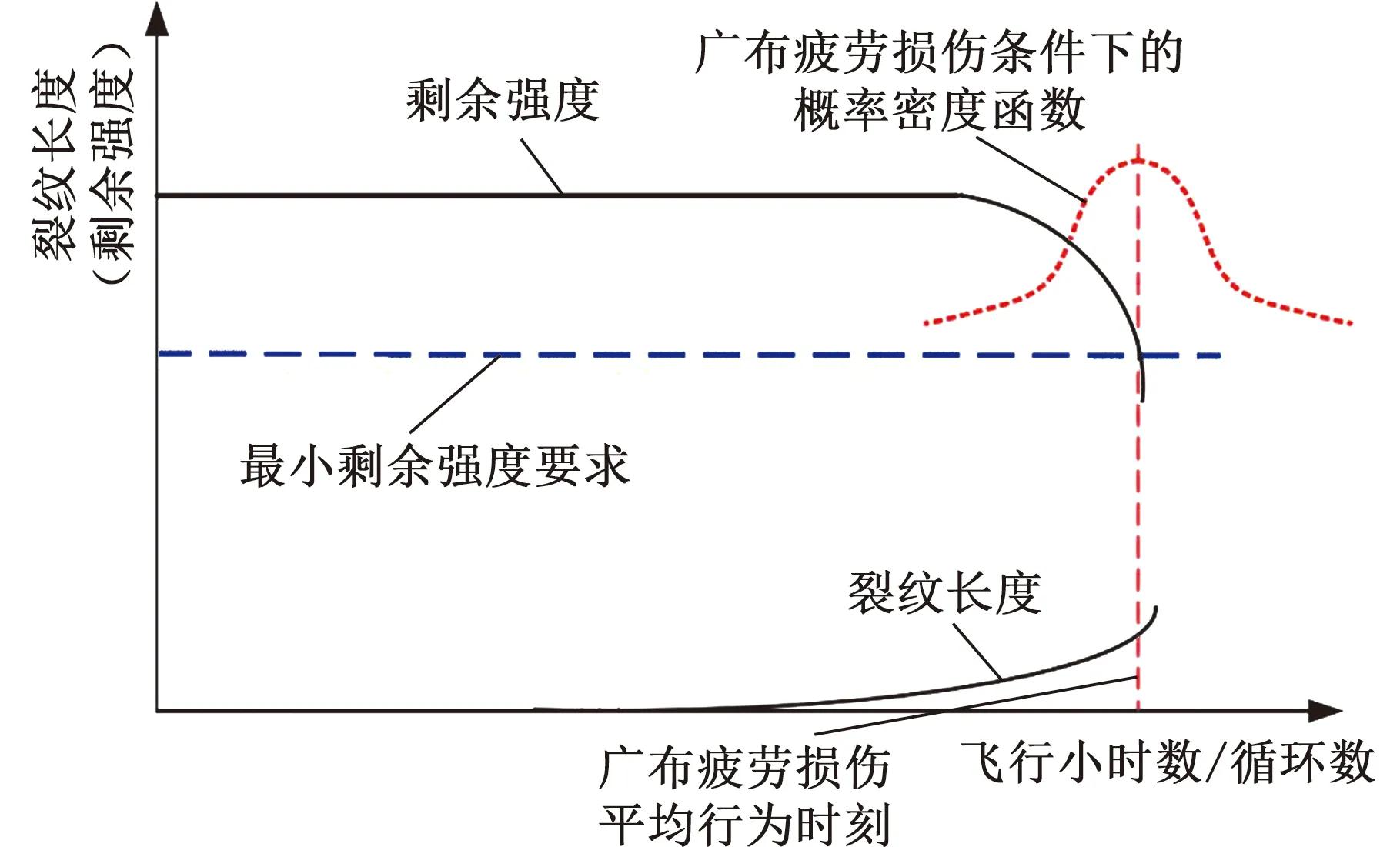
图1 广布疲劳损伤的演变Fig.1 Evolution of widespread fatigue damage
2 随机失效模型
以多隔框机身结构为研究对象,典型的多隔框机身结构如图2所示。当机身的3个隔框失效时,建立广布疲劳损伤条件,失效过程与损伤发生的位置无关。

图2 多隔框机身结构Fig.2 Multi-frame fuselage structure

元件的疲劳特性遵循双参数威布尔分布,威布尔概率密度函数f(t)和累积分布函数F(t)分别为
(1)
(2)
其中,η、β分别为特征寿命和典型形状参数;t为时间变量,表征具体工况的结构寿命时刻。η可以根据N50计算得出:
η=N50(ln2)-1/β
(3)
WHITTAKER等[12]给出了铝的典型形状参数,典型材料的形状参数和特征寿命值[13]见表1。表中,σu为材料极限抗拉强度。
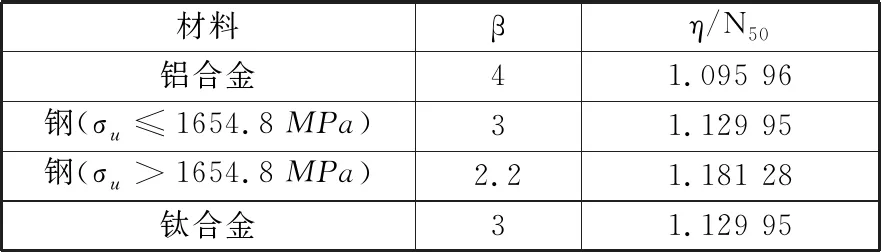
表1 典型材料的形状参数和特征寿命[13]Tab.1 Shape parameters and characteristic life of typical materials[13]
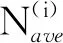

HERNANDES[14]根据个体寿命的对数平均值来定义广布疲劳损伤平均行为时刻,其计算公式为
(4)
式中,n为个体总数。
对于所有元件典型寿命相同的情况,WHITTAKER等[12]给出了一个数值解:
N(t)m,n=
(5)
式中,N(t)m,n为m个元件中n个元件的失效概率;R(t)为关于时间变量t的概率密度函数。
3 算例验证
连续5个隔框的典型疲劳寿命见表2,数据来自试验测试及机队服役数据[14]。其中,FC表示飞行循环数/飞行架次(flight cycles),η(i)为第i个元件的特征寿命。
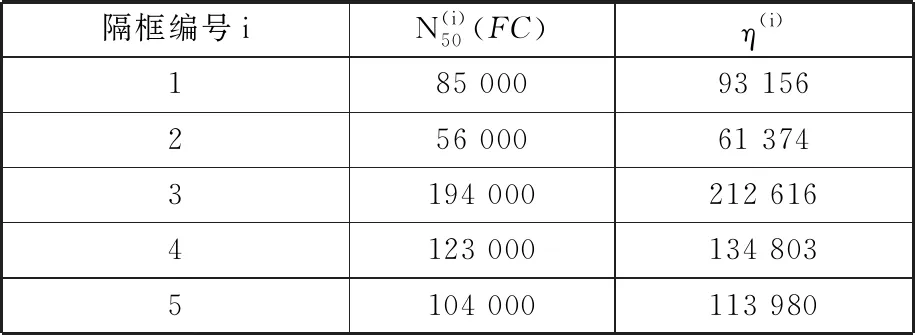
表2 隔框的典型疲劳寿命及特征寿命Tab.2 Typical fatigue life and characteristic life of bulkhead


图3 五个隔框的寿命分布Fig.3 Life distribution of five bulkheads
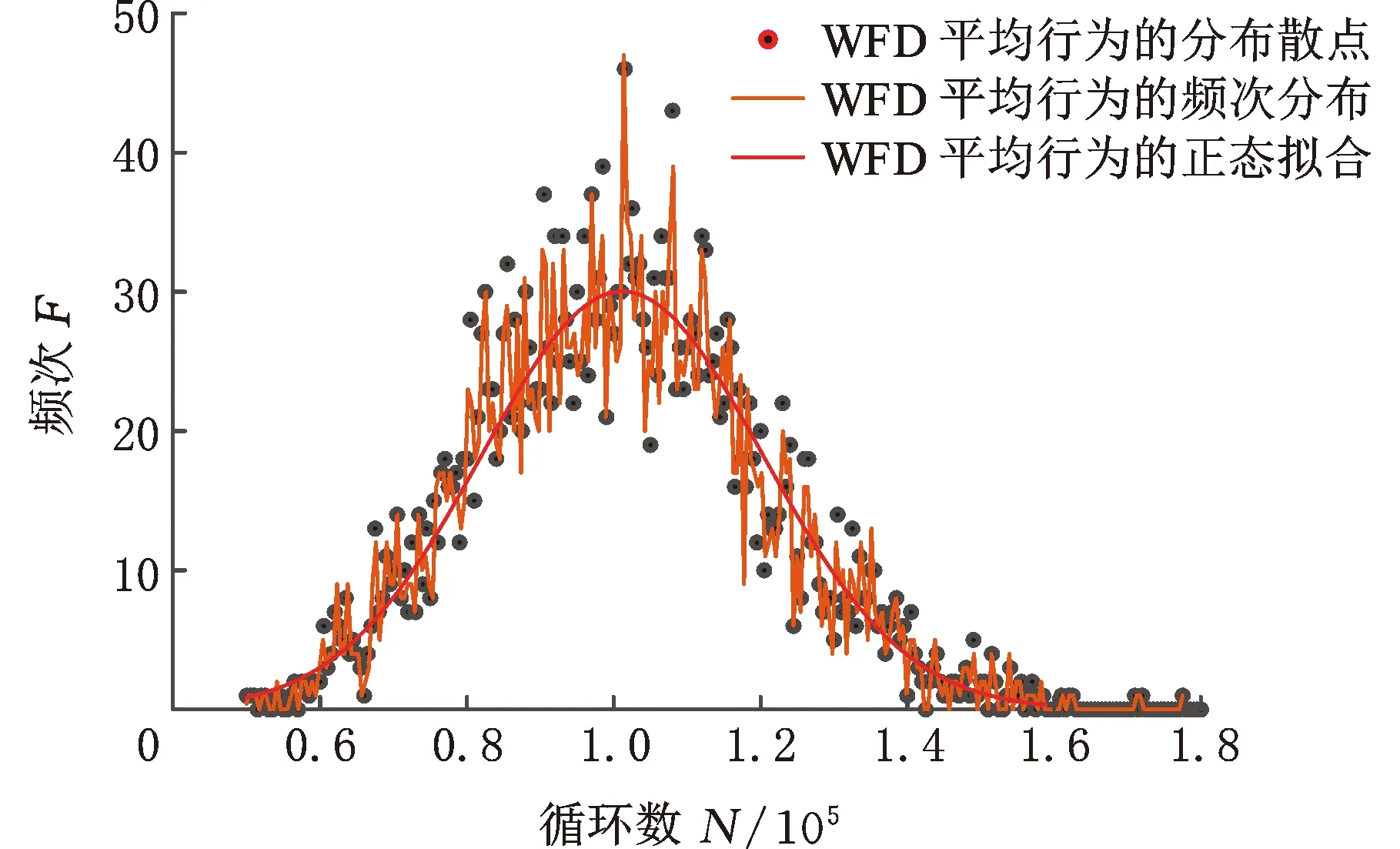
图4 3000次模拟的分布Fig.4 Distribution of of 3000 times simulation


图5 威布尔分布回归检验Fig.5 Weibull distribution regression test


图6 正态分布回归检验Fig.6 Normal distribution regression test
基于上述分析,将五隔框模型评估结果列于表3,可以看出,评估结果与文献[14]中结论基本保持一致,基于威布尔回归得到的结论趋于保守。

表3 威布尔回归与正态回归结果对比Tab.3 Comparison of Weibull regression and normal regression results
对模拟次数n进行分析,通过改变模拟次数来观察评估结果是否趋于收敛。再对五隔框模型分别进行次数为10 000、50 000和100 000次的模拟,结果见表4,表中加粗数字为正态回归结果,其余为威布尔回归结果。可以看出,模拟次数的改变对结果的影响不大,基本可以认为结果处于收敛状态。对比威布尔回归和正态回归的结果可知,由于失效概率较小时威布尔回归的分布参数偏离实际抽样结果,ISP、SMP值较为保守,而广布疲劳损伤平均行为时刻Nave由于对应失效度为50%,此时威布尔分布参数接近实际抽样结果,因此,基于威布尔回归和正态回归的结果基本一致。

表4 模拟结果随模拟次数的变化关系Tab.4 Relationship between simulation results and simulation times
就机队执行初始检查和结构维修行动而言,飞行小时数相比载荷循环数更为直观,更具工程应用价值。飞行小时数与载荷循环数之间的换算需要依据具体飞机结构细节的飞行载荷谱进行,以某飞机结构细节任务剖面的飞行载荷谱[16]为例,100飞行小时对应670.6次循环载荷,将表4中的正态回归评估结果换算为飞行小时数,则初始检查时刻为8234.9飞行小时,结构维修时刻为10 245.5飞行小时。
4 实例分析
LIU[17]开展了七隔框机身段疲劳试验,等直段试验件及试验加载如图7所示。选取真实机身22至28号框位作为试验考核区,试验中多个隔框在相近的部位断裂,后续检查中发现其他框在相同部位出现裂纹或断裂,如图8所示。经应力比较分析,隔框应力水平相当,结构细节相似,根据广布疲劳损伤敏感结构判定原则,判断为多元件损伤。

图7 机身等直段试验件Fig.7 Speciman for straight section of fuselage

图8 隔框损伤情况Fig.8 Damage to the bulkhead

图9 10 000次模拟下的分布Fig.9 Distribution of under 10 000 times simulation
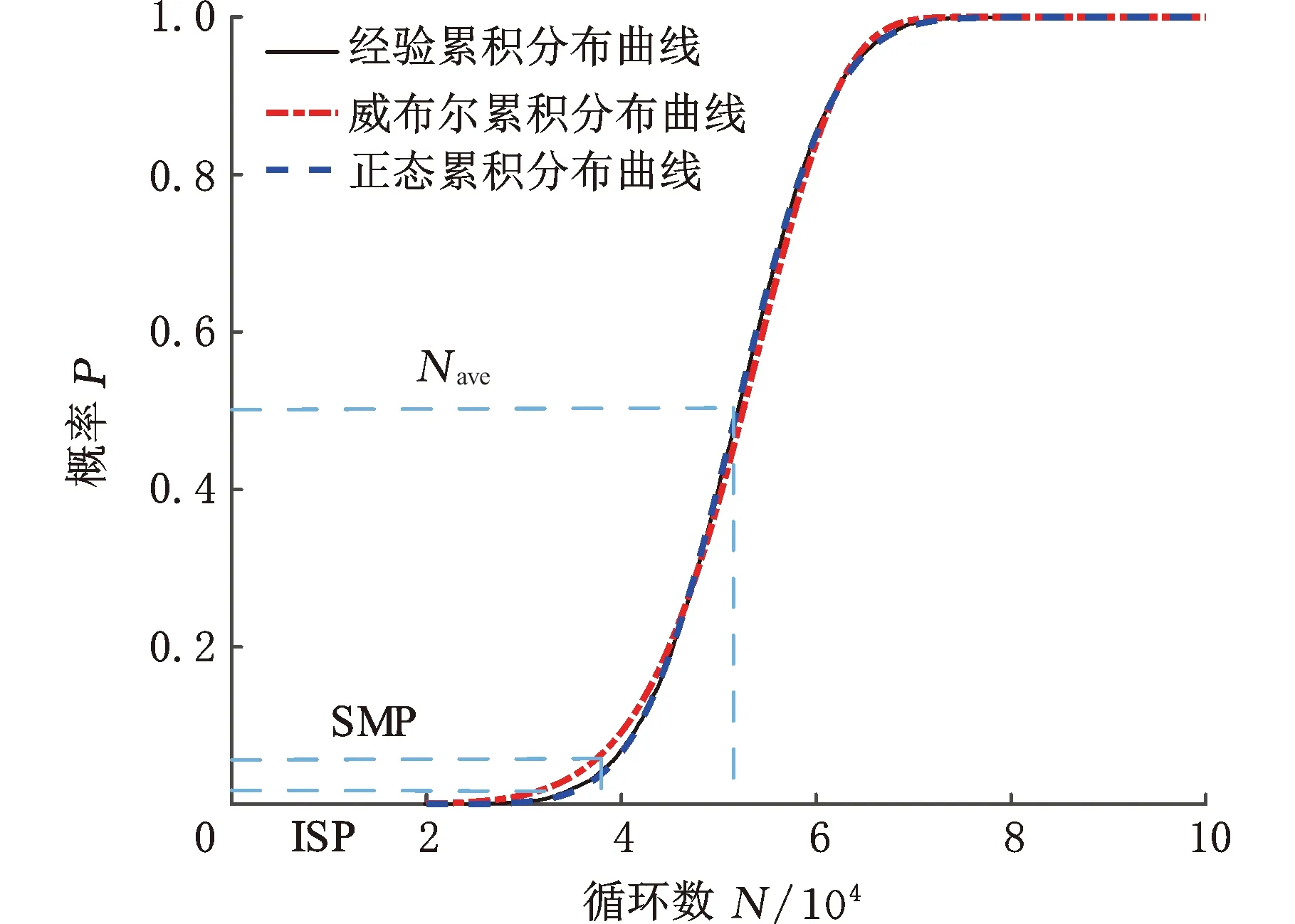
图10 广布疲劳平均行为时刻的概率累计分布Fig.10 Probability cumulative distribution at the time of general fatigue behavior
基于概率模型对机身等直段进行多元件损伤评估,评估结果见表5。

表5 威布尔回归与正态回归结果对比Tab.5 Comparison of Weibull regression and normal regression results
试验载荷谱依据真实飞机机身对接框位的载荷谱等损伤折算得到,疲劳载荷工况为综合工况,试验时同时施加增压载荷和弯矩载荷,一次加载循环代表一次飞行起落。依据某型飞机结构的疲劳载荷总谱[16],每次飞行平均为45 min,将正态回归评估结果换算为飞行小时数,则结构广布疲劳平均行为时刻为34 552飞行小时。
5 结论
(1)通过五隔框机身段验证了随机失效模型的有效性,结果表明:评估结果与算例数据吻合良好,随机失效模型能够给出较好的评估结果。
(3)对模拟次数n进行分析,通过改变模拟次数,观察评估结果是否趋于收敛,结果表明:本文采用的模拟次数足够,评估结果收敛。
(4)根据七隔框机身段疲劳试验结果进行多元件损伤评估,给出结构检查修理时刻,为防止结构设计寿命内发生广布疲劳损伤提供了依据。
