低压直流微电网的改进SoC 均衡控制研究

方 炜，齐 楠，仇 锐，刘晓东，刘宿城

（安徽工业大学电力电子与运动控制省重点实验室 安徽 马鞍山 243032）

随着能源与负荷“即插即用”需求的与日俱增、终端用户负荷直流化趋势明显，直流微电网逐渐成为能源生产消费和技术变革的一项重要支撑[1-2]。其中，低压直流微电网的研究与应用展现出巨大的潜力和市场[3]。

为满足系统的稳定运行、增大容量配置[4]，储能系统（energy storage system, ESS）中各储能单元（energy storage units, ESUs）通常以分布式结构并联接入直流母线[5]。但是随着多个储能单元的接入，各单元之间荷电状态（state of charge, SoC）的不一致将会造成储能单元过度充放电及频繁投切，严重影响到储能元件的使用寿命以及系统的稳定性[6]。

文献[7]利用SoC 的不断变化实时改变下垂系数，实现各储能单元放电过程SoC 以及负荷功率的动态均衡。文献[8]对此做出了进一步展开，将SoC 的n次方分别应用在下垂系数的分子和分母中，实现ESUs 在充放电两种模式下动态均衡，但是控制器中需要选择两种不同的下垂表达式分别控制ESUs 的充电和放电过程。文献[9]将ESUs 的SoC 平均值加入下垂系数中，进而达到SoC 均衡的目的。但加入SoC 后的下垂系数值较大，导致过大的母线电压偏差[10]。文献[11]把与SoC 相关的算法引入下垂控制的参考电压中实现对SoC 均衡速度的控制。而文献[12]提出的控制方案，能够对低压直流微电网实现高精确度、无电压偏差的SoC 均衡目标，但提高了系统的通信压力，且控制器过于复杂提高了其设计成本。

为此，本文提出了一种适用于用户侧低压直流微电网的改进下垂控制策略。本控制方案可以同时用于储能系统的充电和放电过程，不需要采样储能单元的输出电流，降低设计难度的同时，可有效降低母线电压偏差范围；且各储能之间不存在互联通信，降低系统的整体通信压力。其次，依据SoC函数的曲线变化特性提出了曲线法分析系统的动态特性，基于小信号模型分析了系统的稳定性，并由此给出设计参数的选取原则。最后，搭建了基于系统的多储能单元并联的微电网硬件实验平台，通过实验验证所提理论的合理性和有效性。

1 控制模型及运行方式分析

1.1 下垂控制的运行方式

直流微电网中ESUs 传统下垂控制可表达为：

根据上式所述，母线电压与输出电流、下垂系数之间的动态调节关系如图2 所示。图2a 和图2b分别表示下垂系数和参考电压变化时，系统中负荷电流及输出电压出现的改变，利用这一特性，储能系统可实现对系统负荷的自主分配[14-15]。

图1 储能系统等效电路

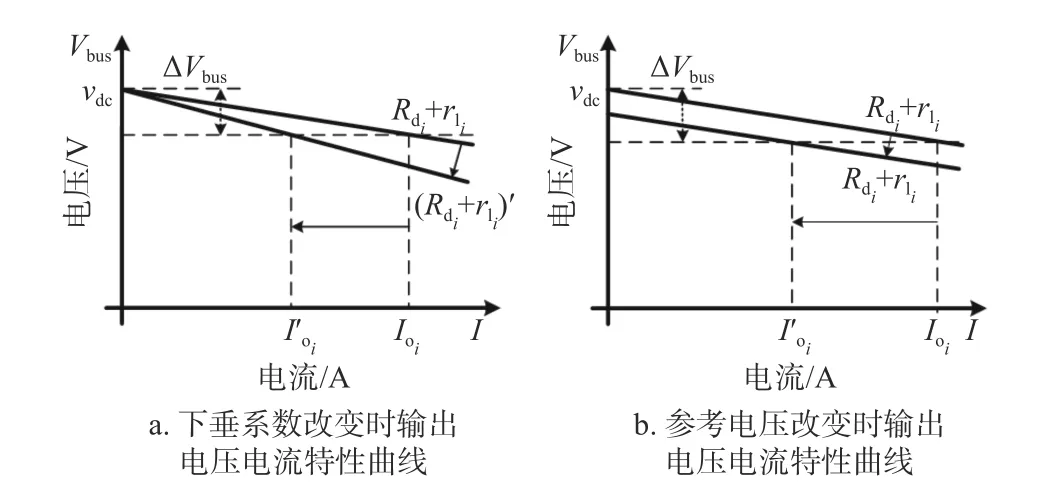
图2 下垂曲线的动态调整过程

1.2 基于SoC 均衡的改进控制方案

本文以用户侧的低压直流微电网为应用对象，以SoC 均衡为控制目标，提出了改进控制方案，如图3 所示，该方案无需各单元之间的互联通信及输出电流采样，简化了控制器设计，且能有效地改善母线电压偏差。

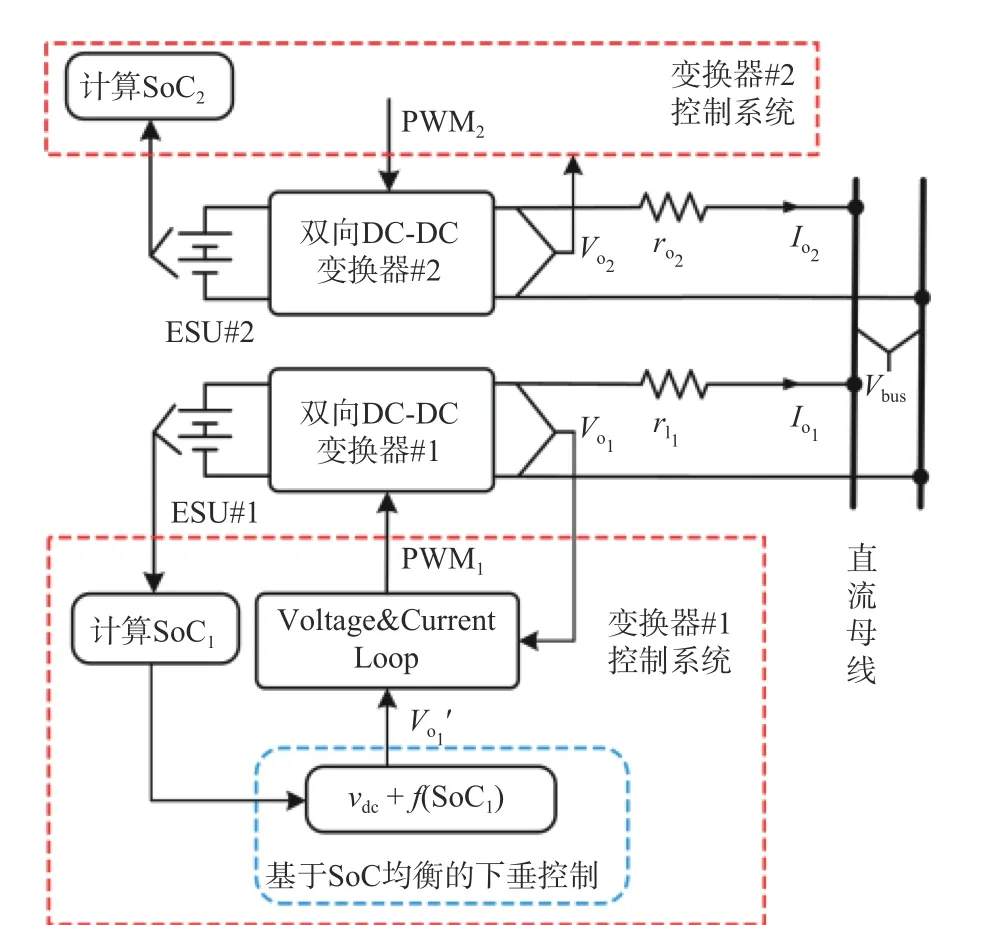
图3 基于SoC 均衡改进下垂控制的系统整体结构

储能单元常用的SoC 计算方式为：

由式（8）可得，变换器的输出电流与其储能单元的SoC 值呈正比关系。故在放电过程中，SoC较大的ESU 提供较多的负荷电流，而SoC 较小的ESU 提供较小的负荷电流。充电过程则相反，最终ESUs 之间的SoC 和电流趋于一致，达成SoC均衡及负荷电流合理分配目标。

2 系统的动态性能及稳定性分析

2.1 曲线法分析系统动态特性

根据式（6）～式（9），函数f（SoC）与输出电流、SoC 的变化率有直接关联。故提出一种曲线法，直观地分析运行过程中系统的SoC 均衡速率。

本文采用的函数f（SoC）表达式为：

式中，k和n分别为比例系数和自变量SoC 的指数系数，作为调节因子来调节SoC 的均衡速率；δ 的取值与函数值域相关，在控制器中作为母线电压偏差调节因子，可控制母线电压偏差范围。为保持ESUs 输出电压恒定，SoC 的取值范围可限制在10%～90%。

图4 分别分析了k和n取值不同时，f（SoC）的曲线变化率。由图4a 所示，保持n不变，随着k值的增大，f（SoC）的曲线变化率明显增大，系统将会获得更快的均衡速率。由图4b 所示，保持k不变，SoC 取值较大时，曲线变化率都随着n的增大而增大，系统有更快的均衡速率；相反，当SoC 取值较小时，曲线变化率会随n的增大而变低，相应均衡速率也会降低。

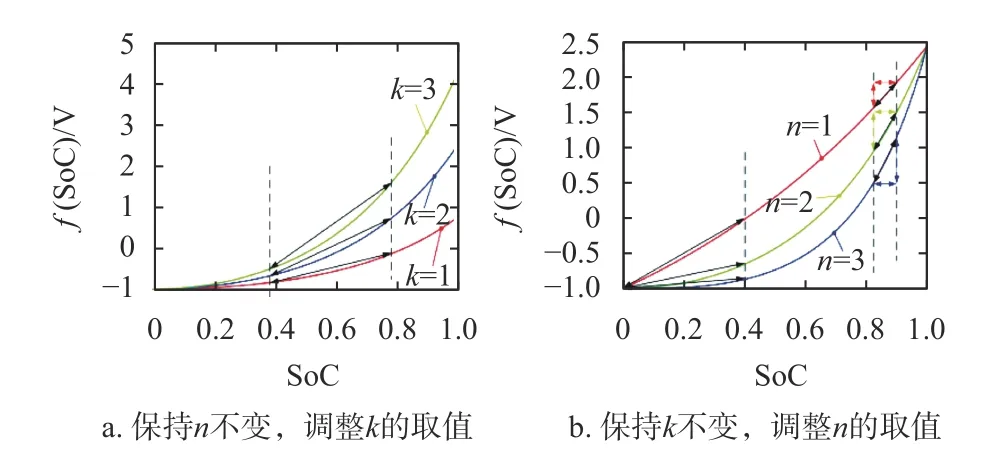
图4 不同调节因子所对应的曲线变化率

进一步，由式（5）可得母线电压与函数f（SoC）的关系，若忽略线路电阻引起的少量压降，f（SoC）取值即可近似为母线电压偏差，f（SoC）的值域即为母线电压的偏差范围。图5 比较了δ 取值不同时的函数曲线，调节因子δ 取值不同时，对应f（SoC）值各不相同，即母线电压偏差范围。

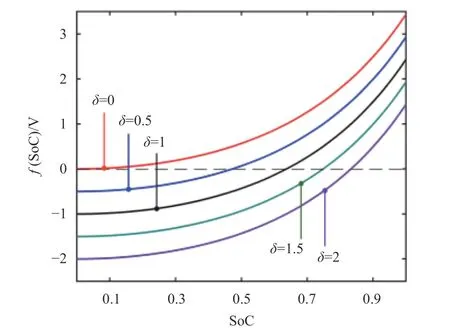
图5 不同δ 取值时的母线电压偏差分布

根据上述曲线法的分析，只需保证控制器中选取的函数f（SoC）曲线特性合理，即可达到控制均衡速率和改善母线电压偏差的目的。

2.2 稳定性分析

对式（3）进行小信号扰动，得：

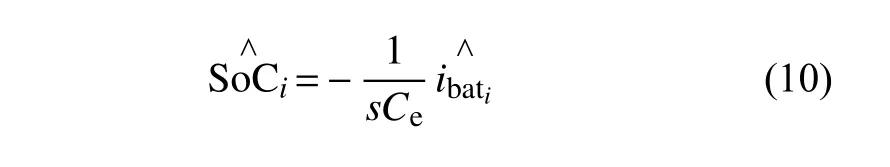
式中，变换器的输入电流Ibati和输出电流Ioi之间的比例关系可写为：

对式（5）和式（9）联立后进行小信号扰动，可得：

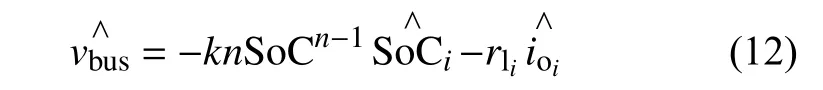
将式（10）和式（11）代入式（12），有：

ESUs 在放电过程中，能量流动方式可简化为：

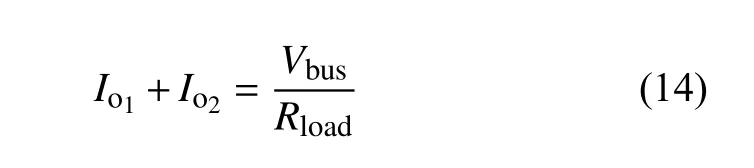
式中，Rload视为系统放电过程中的等效负载。

相应的，ESUs 在充电过程中，能量流动过程的稳态可以依据文献[16]分析：

式中，Icps为系统向ESUs 充电的恒功率源输出电流；Pcps为恒功率源的输出功率大小，在稳态条件下可视为常数；vbus_op为母线电压额定值；R′为系统的实际负载大小，取正值。

联立式（15）和式（16）可得：

式中，Rload同放电过程一样，可视为系统在充电过程中的等效负载。需要指出的一点是，系统在放电过程中，等效负载Rload取正值，而在充电过程中，等效负载Rload取负值。

式（14）、式（19）进行小信号扰动后均可得到：

（4）题库自测模块：提供学生自行检测的题库。通过菜单链接到比较知名的计算机等级考试模拟自测系统中，以供学生课外复习。

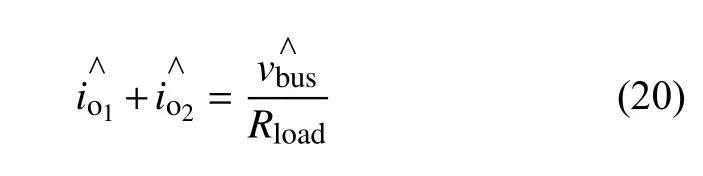
联立式（13）和式（20），可得系统的特征方程：

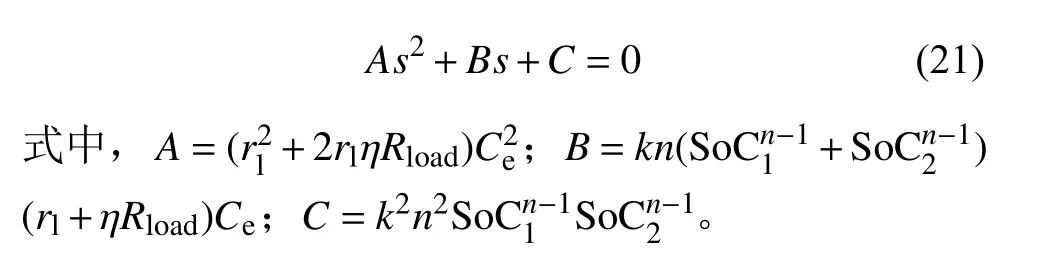
由于系统ESUs 之间为相互等价，如图6 所示保持SoC1不变的同时，绘制SoC2在合理范围内变化的根轨迹图，以对所提控制策略进行稳定性分析。用于计算的系统参数选择如表1 所示。

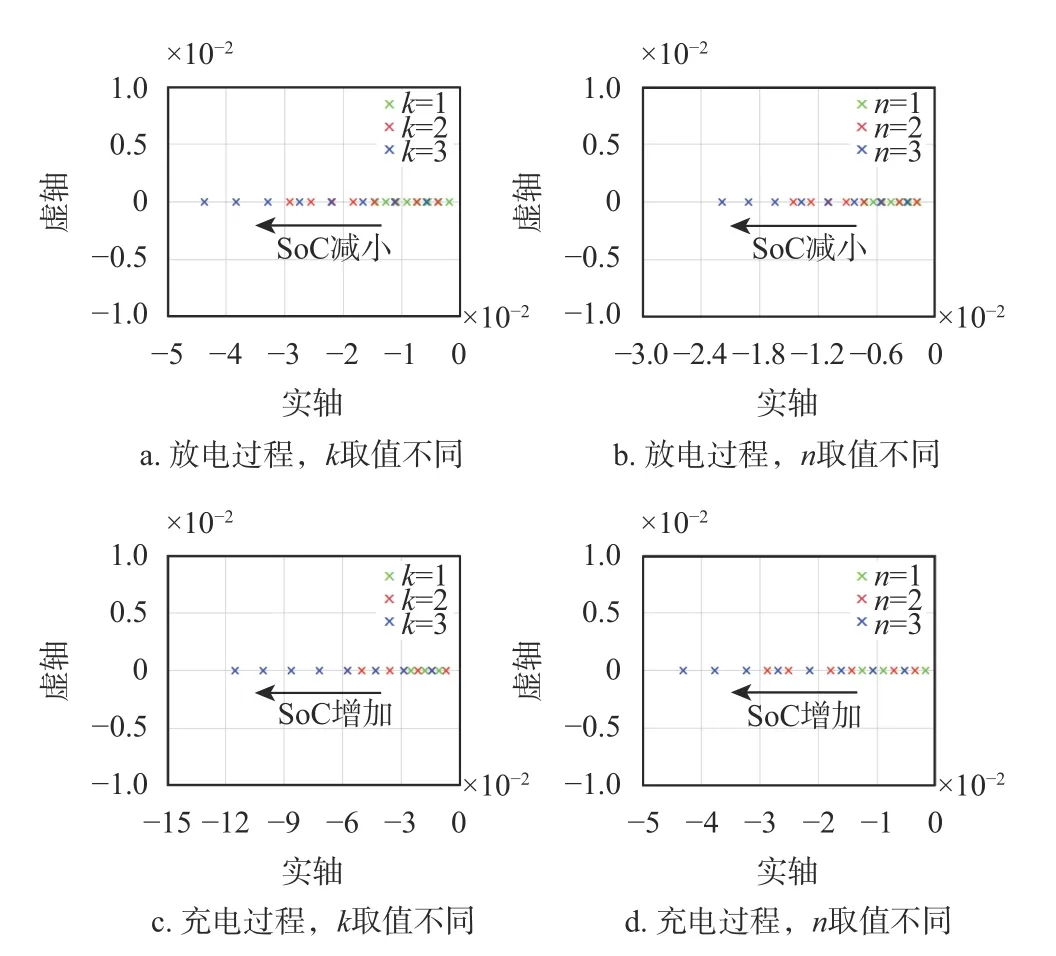
图6 调节因子不同和SoC 变化情况下的根轨迹分布

表1 直流微电网系统相关参数

图6 绘制了调节因子取值不相同情况下SoC2变化时的根轨迹图。不同颜色标记代表着调节因子的不同取值，相同颜色标记了SoC 变化情况下的闭环主导极点。系统的主导极点均分布在s域的左半部，系统的稳定性得到保证。

2.3 控制系统设计规则

在所提改进控制系统的应用设计过程中，相关约束条件及参数的选取需从以下方面具体考虑。

1）参数选取：对于初始SoC 较大的情况，控制系统中可以取较大的n和k加速SoC 均衡；对于初始SoC 较小的情况，可以选择较小的n和较大的k以提高均衡速率。

2）约束条件1：f（SoC）中3 个调节因子的变动，可能会造成母线电压偏差过大。结合曲线法初步预估母线电压的偏差范围，适当调节f（SoC）的曲线特性，确保系统在运行中母线电压始终在最大允许范围内波动，同时由式（5）量化f（SoC）的取值范围：

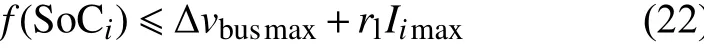
3）约束条件2：在设计过程中，控制系统中f（SoC）还受最大充放电电流及接口变换器的功率等级限定。根据式（8）输出电流与f（SoC）的关系，可表达为：

式中，Iload为流过储能系统的最大输出（输出）电流值；verr为直流母线偏差。以此量化参数作为参考，在实际设计中，保证输出电流不高于最大功率限制和充放电电流限制即可满足参数选取要求。

3 实验验证

硬件实验平台如图7 所示。为了提高实验效率缩短实验时间，选择了两组21 V/1.6 Ah 规格的小容量锂电池组，并依据电池组规格匹配了额定功率为200 W 的双向Buck/Boost 变换器；光伏阵列由可编程电源模拟，接变换器实现MPPT 运行。控制策略均由TI_DSP28335 数字控制器实现，储能单元控制器对电感电流的限幅范围将设置在-3.5 ～8 A。锂电池组的SoC 采用开路电压法结合安时积分法对进行在线估算，由DSP 记录所得SoC 数据，绘制点线图作为SoC 的最终实验结果。

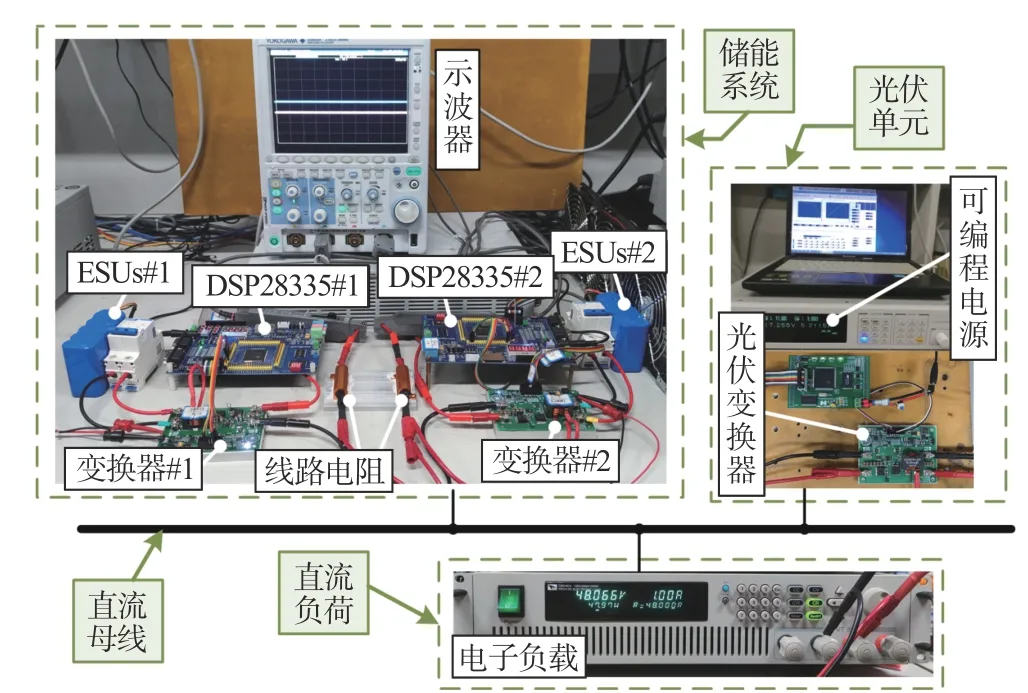
图7 带有储能系统的实验平台

3.1 放电实验

当光伏单元的输出功率不足以满足负荷需求时，储能单元工作在放电模式下向负载供电。初始SoC1_0=0.9，SoC2_0=0.8；锂电池放电电流不超过8 A，折算至输出电流Io最大值不超过3.3 A。故根据选取原则，k=2，n=1，δ=1，实验波形如图8 所示。

图8 放电过程实验波形

图中的各储能单元均衡前，SoC 初始值较大的ESU#1 输出电流大于ESU#2 的输出电流，SoC1的下降速度明显快于SoC2的下降速度。随着系统的运行，各单元输出电流Io和SoC 逐渐趋于一致，约80 s 时刻实现储能系统输出电流均衡分配及SoC 均衡。系统整体运行过程中，母线电压偏差约0.4 V，说明所提策略可有效控制母线电压偏差。

3.2 充电实验

当光伏单元的输出功率多于负荷需求时，储能单元工作在充电模式下吸收多余的电能。初始SoC1_0=0.35，SoC2_0=0.30，低压侧锂电池充电电流不超过3.6 A，折算在变换器高压侧电流不超过约1.8 A。根据选取原则，k=1，n=1.5，δ=1，实验波形如图9 所示。图中，SoC 较小的ESU#2 吸收的电流明显大于ESU#1 吸收的电流，同样，ESU#2中SoC 上升速率明显快于ESU#1。随着系统的运行至100 s 时刻，两个储能单元之间的SoC 差值逐渐减小，负荷电流也逐渐趋于一致。同时，图9c所示的母线电压也无明显偏差，说明在充电过程中，所提策略依然可有效控制母线电压偏差。所提改进控制策略的有效性得以验证。

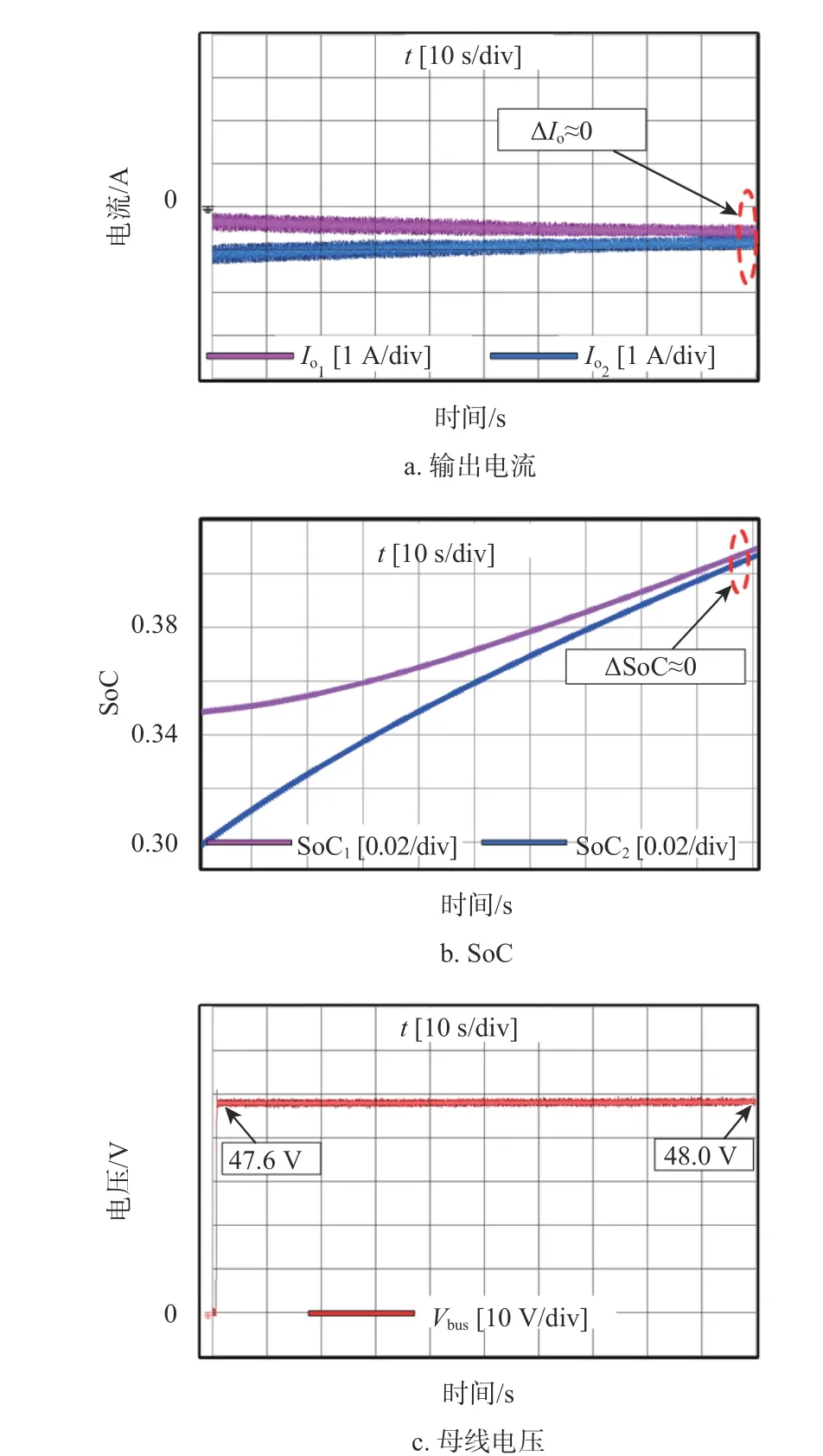
图9 充电过程实验波形

3.3 负载跳变实验

图10 模拟了放电过程中的负载跳变情况，负载跳变1 由4 A 减小为2 A，输出电流和SoC 变化率均减小，但SoC 较高的ESU#1 输出电流依然大于ESU#2 的输出电流；负载跳变2 时刻负载电流恢复，储能单元输出电流增大。整个过程中，各单元输出电流及SoC 变化趋势并未发生变化，随着系统的运行最终均趋于一致。

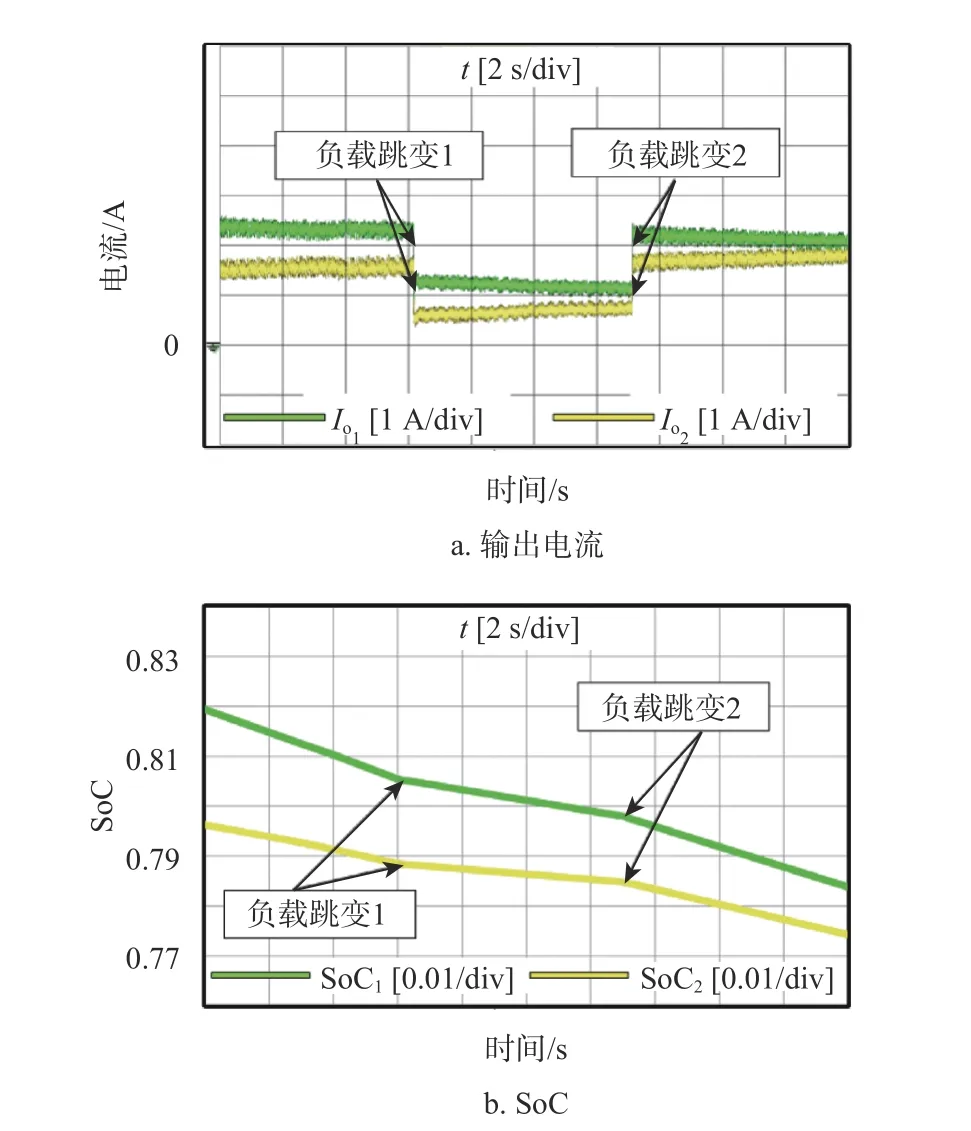
图10 储能系统放电跳变实验波形

图11 为系统充电过程中负载功率突变的实验波形。与放电过程相似，储能系统的充电电流出现变化后，各储能单元重新分配负荷电流，SoC 的变换率也出现相应改变，并最终趋于一致，实现了储能单元间的SoC 均衡控制。

图11 储能系统充电跳变实验波形

4 结 束 语

本文针对适用于用户侧的低压直流微电网系统的多储能单元SoC 状态不一致问题，提出了改进的自适应下垂控制策略；同时应用曲线法分析系统在该控制策略下的动态特性，并据此给出控制器参数的设计思路。理论分析以及最终的实验结果表明：

1） 所提改进控制方案以保证较小的母线电压偏差为前提，可以同时实现系统充电和放电工作过程的SoC 均衡；

2） 在用户侧低压直流供电系统运行效果基本不受影响的前提下，控制器的设计中省略了对输出电流的采样以及各储能单元之间的互联通信，可以有效降低系统控制器的设计难度和设计成本。