SM4 密码算法S 盒的量子电路实现

罗庆斌，李晓瑜，杨国武

（1. 湖北民族大学信息工程学院 湖北 恩施 445000；2. 电子科技大学信息与软件工程学院 成都 610054；3. 电子科技大学计算机科学与工程学院 成都 611731）

量子计算极大地改变了现代密码系统的安全性。对于非对称密码系统，Shor 算法[1]能快速破解基于大整数分解的密码算法[2]和基于离散对数的密码算法[3]。量子计算对于对称密码系统的影响虽然没有像非对称密码系统那样显著，但最近也得到大量关注。文献[4]首先分析了Grover 算法[5]对对称密码系统的量子威胁，建议把原来的密钥长度至少增加一倍。文献[6]利用Simon 算法[7]寻找碰撞周期以攻击对称密码系统，一些在经典环境中需要Ω(2n/2)次查询的密码算法在该量子环境下只需要O(n)次查询。文献[8]结合Grover 算法和Simon 算法对具有FX 结构的对称密码在量子环境下的安全性进行了分析。文献[9]结合Grover 算法和Simon算法对具有Feistel 结构的对称密码算法提出了量子密钥恢复攻击。文献[10]通过在量子环境下利用Demirci-Selçuk 中间人攻击和提高解S 盒差分方程的效率分析了AES 密码算法在量子环境下的安全性。文献[11]利用Grover 算法和Simon 算法为SM4 密码算法构造了一个8 轮的量子区分器。

这些对称密码在量子环境下的安全性分析基本是建立在它们已经可以用量子电路实现的假设上的。但是目前针对对称密码算法的量子电路实现研究较少，且基本是对AES 密码算法的量子电路实现[12-13]，其他对称密码算法量子电路实现的研究几乎没有。

SM4 算法是用于WAPI 的分组密码算法，2006年由我国国家密码管理局公开发布[14]，2012 年3 月发布成为国家密码行业标准[15]（标准号为 GM/T 0002-2012），2016 年8 月发布成为国家标准[16]（标准号为 GB/T 32907-2016），2021 年6 月发布成为国际标准[17]（标准号为 ISO/IEC 18033-3：2010/AMD1：2021）。SM4 算法的安全性自发布以来，得到了广泛的关注。在这些安全性分析中，SM4 算法中唯一的非线性变换S 盒起着关键性的作用。文献[18]分析了SM4 算法中最小活跃S 盒个数与抵抗差分攻击轮数之间的关系。文献[19-20]分别提出了基于掩码的S 盒实现方案和基于门限理论的S 盒的实现方案，以提高SM4 密码算法的安全性。

本文主要通过SM4 密码算法S 盒的代数结构，使用NOT 门、CNOT 门和Toffoli 门构建实现S 盒的量子电路。

1 SM4 密码算法

SM4 算法是分组密码算法，其数据分组长度和密钥分组长度都为128 bit。加密算法与解密算法都以字节（8 位）和字（32 位）为单位进行数据处理。

1.1 加密算法

加密算法采用32 轮迭代结构，每轮使用一个轮密钥。

设输入明文为 (X0,X1,X2,X3)∈(GF(232))4，输出的 密 文 为 (Y0,Y1,Y2,Y3)∈(GF(232))4，rki∈GF(232)(i=0,1,2,···,31)为轮密钥。加密算法可描述如下：

式中，i=0,1,2,···,31，则有：

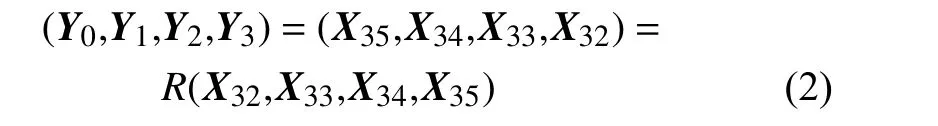
式中，F是轮函数，变换T:GF(232)→GF(232)由非线性变换τ 和线性变换L构成，即：

变换 τ由4 个8 bit 的非线性变换S 盒并行构成。设A=(α0,α1,α2,α3)∈(GF(28))4是非线性变换τ的输入，B=(β0,β1,β2,β3)∈(GF(28))4是输出，则变换τ 定义如下：

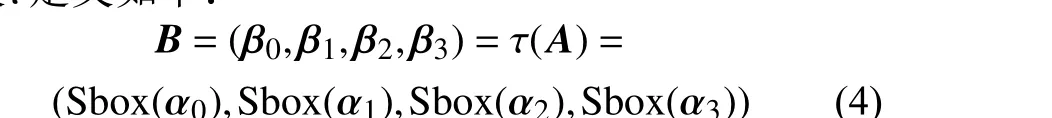
式中， S box(·)为以字节为单位的非线性替换。S 盒的替换表可以参考文献[18]，将在第2 章介绍它的代数结构。

变换 τ 的 输出B将作为线性变换L的输入。设C∈GF(232)是L的输出。则线性变换L定义为：

式中，＜ ＜＜i表 示把32 位字循环左移i位。

SM4 密码算法的加密过程如图1 所示。由于解密算法和加密算法采用相同的变换结构和过程，只是反序使用轮密钥，这里不再赘述。

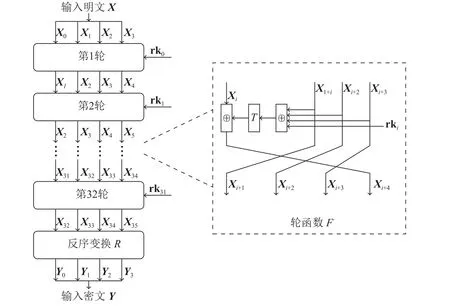
图1 SM4 分组密码算法加密过程

1.2 密钥扩展算法

2 S 盒的代数结构

在SM4 密码算法中，S 盒是唯一的非线性变换，是保证安全的关键组件。S 盒通常由256 个元素构成的查询表描述。文献[21]研究了S 盒的代数结构，并给出了如下的具体表达式：

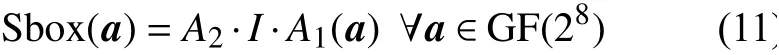
GF(28)

式中，I是 上的乘法逆元，这里的不可约多项式为：

3 S 盒的量子电路

3.1 实现思路分析

用量子电路实现S 盒，实际上就是实现式（11）。在式（11）中仿射变换的表达式已经由式（13）给出，可以用类似高斯消元的方式实现矩阵FT，即通过行变换把矩阵FT化成单位阵，每做一次行变换便在对应量子电路中添加一个CNOT门，反序排列这些CNOT 门，便构造出了矩阵FT的量子电路。对于列向量v，在出现“1”的对应位置添加NOT 门便可实现。

乘法逆元I会相对复杂。文献[22]证明了GF(2n) 上 的任一非零元素a的逆元可以表示成(a)-1=(a)2n-2。因此需要计算：

因 此，可 以 得 出： ∀a∈GF(2)[x]/(f(x))，有a2=Sq·a，其中：

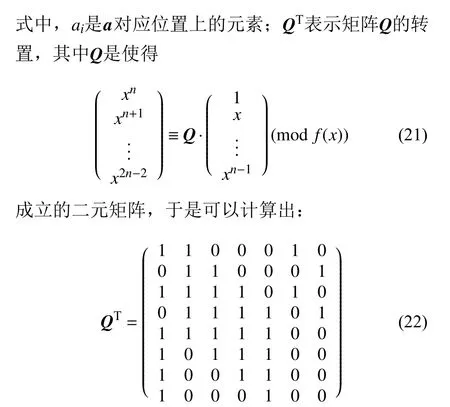
3.2 量子电路实现

本文使用Python 语言并利用qiskit 软件包实现所求的量子电路。对于式（13）中仿射变换的表达式，使用高斯消元法实现矩阵FT，并通过在对应位置添加NOT 的方法实现向量v，最终式（13）中仿射变换的量子电路如图2 所示。 G F(28)上的平方计算可以通过式（17）的线性变换表示，利用高斯消元法实现平方计算的量子电路如图3 所示。式（19）和式（20）中的d和e可以通过Toffoli 门实现，式（22）中的矩阵QT可以通过高斯消元法实现，因此式（18）便可以实现，量子电路如图4 所示。

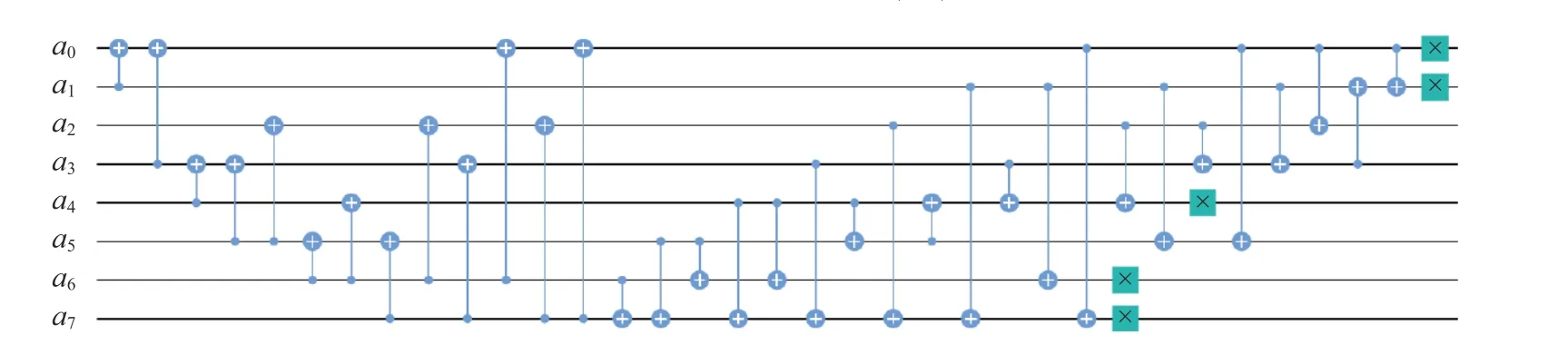
图2 实现式（13）仿射变换的量子电路图

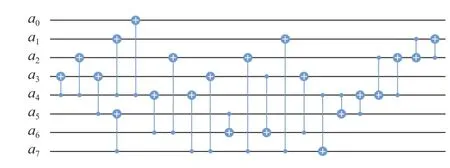
图3 实现式（17）平方计算的量子电路图

为了更快速地计算I(a)=a254，本文采用Itoh-Tsujii 算法[24]，但为了尽可能少地使用辅助量子比特，把计算顺序调整如下：

1）(a)2=a2

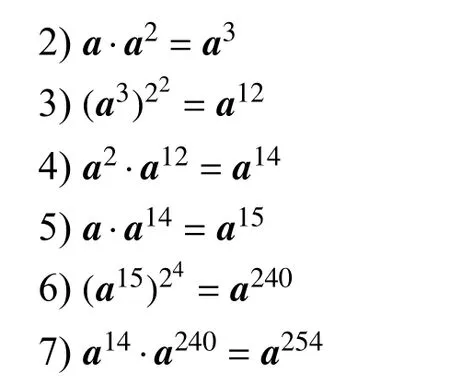
由于仿射变换和平方计算的量子电路都为8 量子比特，乘法计算量子电路为24 量子比特，为了更加方便地表示S 盒的量子电路，本文以8 量子比特为单位描述S 盒的量子电路。记A1和A2为图2 中实现仿射变换的量子电路；Sq 为图3 中实现平方计算的量子电路；图4 中实现乘法计算量子电路的乘数输入分别记为两个实心圆点，乘积结果记为M。主要根据计算a254的步骤，可以得出S 盒的量子电路如图5所示。

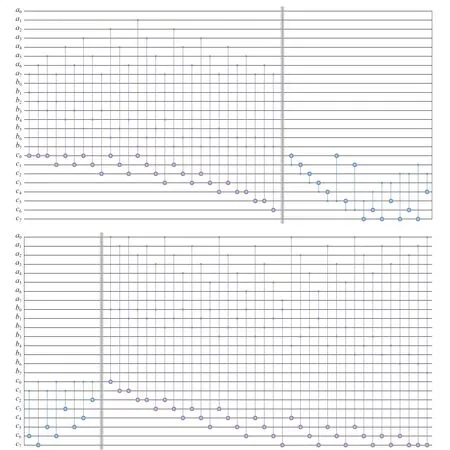
图4 实现式（18）乘法计算的量子电路图

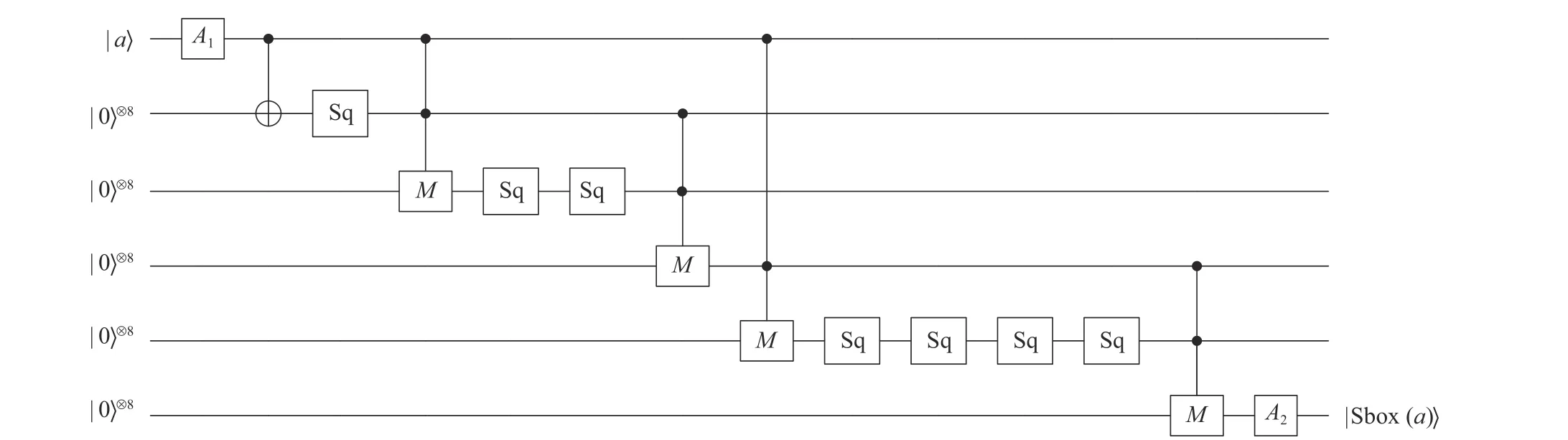
图5 S 盒的量子电路示意图

3.3 量子电路复杂度分析

这里的量子电路是利用NCT 门库实现，即采用NOT 门、CNOT 门和Toffoli 门实现。通过这些量子电路所用量子比特的数量、量子门的数量和量子电路的深度描述构建的量子电路的复杂度如表1 所示。

表1 量子电路所用量子资源情况表

由图5 可知，最终S 盒的实现电路中需要2 次调用仿射变换的量子电路，每个仿射变换的量子电路由34 个CNOT 门和5 个NOT 门构成，电路深度为23；需要7 次调用平方计算的量子电路，每个平方计算的量子电路由22 个CNOT 门构成，电路深度为16；需要4 次调用乘法计算的量子电路，每个乘法计算的量子电路由64 个Toffoli 门和24 个CNOT 门构成，电路深度为39；此外还需要用1 组（8 个）CNOT 门对量子比特进行复制。整个S 盒的量子电路中一共使用了48 个量子比特，592 个量子门，电路深度为289。由于本文是首次实现SM4 密码算法S 盒的量子电路，不能通过对比的方式来分析该电路的复杂度。但文献[12]实现了AES 密码算法S 盒的量子电路，在该量子电路中，共使用了3 组（24 个）CNOT 门对量子比特进行复制，使用的量子比特数为56。由此可以看出，本文实现的SM4 算法S 盒的量子电路还是比较高效的。

4 结 束 语

本文首次给出了SM4 密码算法S 盒的量子电路。根据S 盒的代数结构，首先给出S 盒代数表达式中仿射变换的量子电路，然后把代数表达式中求GF(28)下元素的逆元转换为求该元素的254 次方，为此，分别构建了 G F(28)中平方计算的量子电路和乘法计算的量子电路，再通过改进的Itoh-Tsujii 算法给出S 盒的量子电路。所构建的S 盒的量子电路共使用了48 个量子比特，592 个量子门，电路深度为289。本文的研究将对量子环境下SM4 密码算法的研究产生积极影响。