复杂曲面铝反射镜磁流变抛光工艺优化

徐超，胡皓，彭小强,*，李信磊，林之凡

1. 国防科技大学 装备综合保障技术重点实验室，长沙 410073 2. 国防科技大学 智能科学学院，长沙 410073

飞机等装备平台上的探测光学系统是获取环境信息的重要设备，其性能对信息的获取起到至关重要的作用。相关领域的应用需求对光学系统的重量、体积、制造精度、光机一体化等方面提出了严苛要求。反射镜是光学系统中的核心零部件，在光学系统中采用复杂曲面反射镜能够简化光学系统结构、减轻系统质量、提供更加灵活的系统布局，使系统拥有更高的设计自由度[1]。常用于制作反射镜的材料有石英玻璃、单晶硅、SiC等，但光学玻璃因强度低导致反射镜实现轻量化困难，SiC 硬度大难以加工，应用这些材料加工反射镜时成形难、加工效率低，制作的光学系统也有抗过载能力差、装调困难等问题，难以满足探测光学系统的使用需求[2-4]。使用金属铝材料制作光学反射镜具有质量轻、材料可加工性好、容易实现复杂曲面成型、可实现高轻量化率等诸多优点，且安装支撑光学系统的零部件可以和反射镜采用同种铝材料，进行无热化的光机一体结构设计，避免了反射镜和安装结构部件热膨胀率不一致带来的不利影响[5-8]。因此复杂曲面铝反射镜得到了广泛的应用，例如美国在HM60直升机、MQ1“捕食者”无人机和MQ9“收割者”无人机等平台上都布置了雷神公司生产的复杂曲面铝反射镜光学探测系统[9]。

单点金刚石车削(Single Point Diamond Turning, SPDT)技术适应复杂曲面加工且加工效率高，是目前加工复杂曲面铝反射镜的主要加工手段[10-12]。但SPDT超精密车削加工后的铝反射镜只能满足红外光谱区域的应用条件，若要达到可见光光谱区域及更高的应用需求，需要对其进行进一步抛光。传统的抛光方法在加工复杂曲面反射镜尤其是高陡度复杂曲面反射镜时面临抛光盘与反射镜镜面难以完全贴合的问题，材料加工去除量也无法精确控制，难以加工出高精度高质量的复杂曲面反射镜，制约了先进光学系统发展与应用[13-14]。在抛光面形是复杂曲面的镜面时，磁流变抛光(Magnetorheological Finishing, MRF)可以很好地适应复杂曲面局部曲率的变化，易于实现计算机控制、材料的去除效率也较高。磁流变抛光可以获得高质量的反射镜面，能够实现微米级甚至纳米级的材料去除加工，是光学反射镜加工中的一种重要手段[15]。

1 磁流变抛光去除函数建模

1.1 曲面曲率变化对去除函数的影响

磁流变抛光相比于其他抛光技术的突出优势在于其抛光去除函数稳定准确、修形精度高。铝反射镜磁流变抛光机理如图1所示(FS为正压力，FP为剪切力)，磁流变抛光液在正常状态下是可以流动的液体，当其处于梯度磁场中时，会因为磁流变效应变硬、黏度增大，成为具有黏塑性的流体。抛光磨料在磁流变液缎带的上方形成一层柔性抛光模，抛光模与反射镜镜面接触后，在镜面表面会因为发生化学反应而形成一层氧化层，该氧化层的去除比较容易，最终的加工即是通过抛光模与反射镜表面之间的剪切作用对氧化层进行去除。

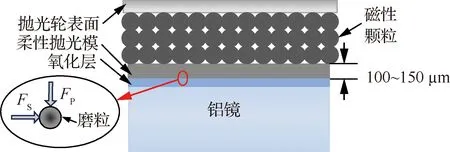
图1 铝反射镜磁流变抛光机理Fig.1 Mechanism of magnetorheological finishing for aluminum mirror

在磁流变抛光时，抛光轮和工件之间的间距会对抛光区域的磁场强度产生直接影响，影响去除函数稳定性，因此在抛光过程中要尽量保持抛光间隙恒定不变。在抛光时，平面工件与抛光轮的抛光间隙不变，陡度较低的非球面工件与抛光轮之间的间隙变化较小，也可认为其近似不变，使用恒定的去除函数就可对该类光学反射镜进行高精度修形。但对复杂曲面进行磁流变抛光时，曲面上各点的曲率不断变化会导致抛光轮与工件之间的抛光间隙也不断发生改变，采用恒去除函数加工时抛光区域的压力和剪切力也会不断的变化，造成去除函数的形状尺寸及去除效率也处于不断变化中，无法实现精确修形。

如图2所示，凹面工件在曲率半径减小的地方抛光间隙减小，抛光去除效率增大，恒去除函数将产生过加工；凹面工件在曲率半径增大的地方抛光间隙增大，抛光去除效率减小，恒去除函数将产生欠加工。凸面工件在曲率半径减小的地方抛光间隙增大，抛光效率减小，恒去除函数将产生欠加工；凸面工件在曲率半径增大的地方，抛光间隙减小，去除效率增大，恒去除函数将产生过加工[16-17]。因此，在对复杂曲面反射镜进行磁流变抛光时，只有获得准确的去除函数，才能获得高质量的加工结果。

图2 工件曲率变化对抛光间隙的影响Fig.2 Effect of workpiece curvature change on finishing gap

1.2 复杂曲面磁流变抛光去除函数建模

获取稳定、准确的去除函数是实现MRF精确抛光的关键技术之一，影响MRF抛光去除函数的因素十分复杂。美国罗彻斯特大学的相关研究表明，工件材料、磁流变液和抛光工艺参数都会对MRF抛光去除函数产生影响，多因素相互耦合导致准确建立MRF抛光去除函数模型十分困难[18]。常用的MRF抛光去除函数建模方法有实验建模法和理论建模法，实验建模法用于平面和简单面形时准确度较高，但不适用于复杂曲面面形；理论建模法在建模过程中有简化和假设的步骤，因此准确度相对实验建模法较低一些。对复杂曲面磁流变抛光去除函数建模，联合使用实验建模法和理论建模法，建模的流程如图3所示，建模步骤为：① 通过实验建模法得到同种铝材料相同工况下MRF抛光的平面去除函数Ff；② 通过分析，建立球面去除函数和平面去除函数的映射关系H(Fs,Ff)，得到球面去除函数Fs：

Fs=H(Ff,Fs)·Ff

(1)

图3 去除函数建模流程Fig.3 Removal function modeling process

③ 在复杂曲面上的任一驻留点d(x,y)处选取一小块区域S，使用最小二乘法拟合出此区域的最接近球面；④在步骤③中拟合得到的最接近球面，通过步骤②的方法获得其球面去除函数，用该球面去除函数近似作为复杂曲面驻留点d处的去除函数；⑤ 依次遍历复杂曲面内的所有驻留点di(i=1, 2,…,n)，得到复杂曲面磁流变抛光的去除函数。

1.3 去除函数驻留时间求解仿真

由计算机控制光学表面成形(Computer Controlled Optical Surfacing, CCOS)的加工原理可知，光学零件抛光时材料的去除量H(x,y) 等于抛光工具形成的去除函数R(x,y) 与抛光工具在各个区域的驻留时间T(x,y) 沿着加工轨迹的卷积[19]：

H(x,y)=R(x,y)·T(x,y)

(2)

在已知去除函数的情况下，根据材料去除量的大小，控制抛光工具在各个驻留点的驻留时间，就能够实现对工件面形误差的精确去除。MRF抛光时，驻留时间求解和驻留时间实现是决定面形收敛比和残留误差的关键。驻留时间求解的实质是反卷积运算，求解模型主要有离散卷积模型和线性方程组模型，基于不同的求解模型有不同的驻留时间求解算法[17]。基于离散卷积模型的驻留时间求解算法要求不同加工位置的去除函数相同，适用于去除函数不变的加工，例如抛光平面或球面、忽略随机误差时去除函数可以看作是恒定的。相比离散卷积模型，基于线性方程组模型的驻留时间求解算法可广泛适用于随加工位置变化的去除函数，该算法具有诸多优点：面形误差控制点和加工驻留点的离散网格可以采用不同的网格划分，且可以采用非均匀网格；驻留点数可以少于、等于或多于面形误差控制点数；去除函数和工件可具有任意几何形状，且随着空间位置变化的去除函数也可以适用。采用线性方程组模型求解复杂曲面铝反射镜磁流变抛光去除函数驻留时间，具体方法如下。

如图4所示，对初始面形误差进行离散式网格划分，得到一系列面形误差控制点，将网格的交叉点叫作面形误差控制节点pi(xi,yi)，其中第i个面形误差控制点的坐标为(xi,yi)，对应的离散式网格面形误差值为hi，面积为ai。定义抛光过程中去除函数的驻留位置为驻留点dk(xk,yk)，其中第j个驻留点处的驻留时间为tj。按一定顺序排列，得到控制节点向量：

P=[p1,p2,…,pi,…,pm]T

(3)

面形误差向量：

H=[h1,h2,…,hi,…,hm]T

(4)

驻留点向量：

D=[d1,d2,…,dk,…,dn]T

(5)

驻留时间向量：

T=[t1,t2,…,tj,…,tn]T

(6)

图4 面形误差和去除函数数据离散Fig.4 Surface error and removal function data discretization

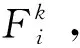
(7)

式中：r(xi,yi)为磁流变抛光模的位置在驻留点dk(xk,yk)时控制点(xi,yi)处的去除函数分布函数。Sin为控制点在去除函数内的区域，控制节点pi位于去除函数的外部区域时r(xi,yi)=0。设去除函数在驻留点dk(xk,yk)对所有控制节点的材料去除量为

(8)

可得到材料去除速率矩阵表示为

(9)

那么，式(2)可以用线性方程组矩阵表示为

Fmn·T=H

(10)

即

(11)

对一块经过SPDT超精密车削加工后的复杂曲面铝反射镜进行仿真，以验证上述分析。SPDT加工后的该反射镜面形为0.809λ(λ为波长)PV(峰谷值)，0.137λ RMS(均方根值)。其面形表达式为

C1x+C2y+C3x2+C4xy+C5y2

(12)

式中：各参数如表1所示。

表1 复杂曲面铝反射镜镜面形表达式参数

对此铝反射镜进行MRF仿真加工，利用1.2节中的计算方法获得复杂曲面铝反射镜上各个驻留点处的动态去除函数，依据本节给出的MRF抛光去除函数驻留时间算法，求出驻留时间分布及面形残差分布，如图5所示。

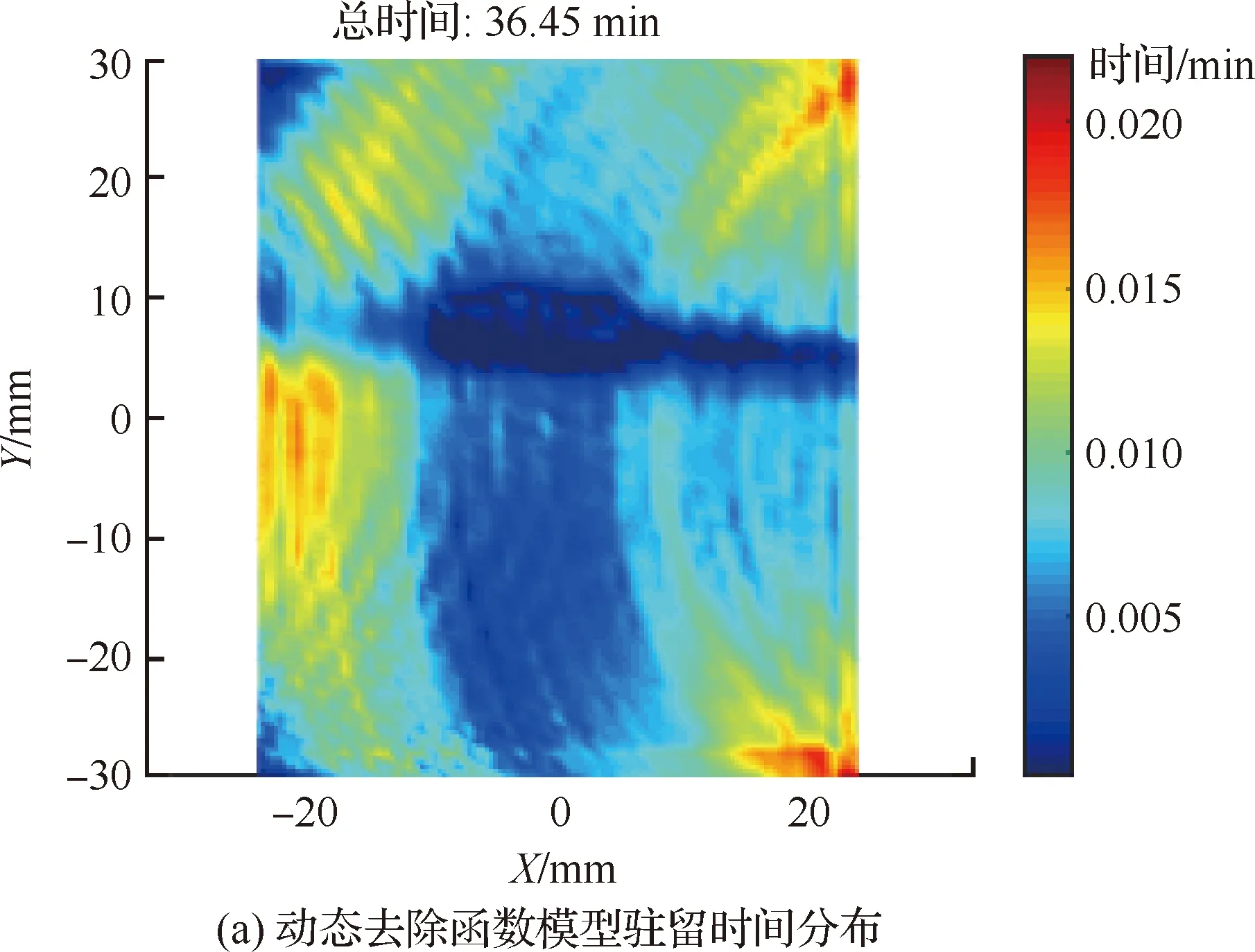
图5 去除函数模型驻留时间及面形残差分布Fig.5 Residence time of removal function model and residual distribution of surface shape

2 磁流变抛光路径优化

2.1 路径规划算法

由第1节分析可知，复杂曲面的面形特征是不断变化的，这意味着MRF抛光时抛光路径的选择具有多样性。复杂曲面面形不断变化的曲率会使去除函数产生非线性变化，对去除函数的稳定性造成不利影响。为了得到稳定的MRF抛光去除函数，需要对抛光路径进行规划[20-22]。以曲率变化最小方向为原则，有2种规划方式：一种是局部最优，路径方向为当前控制点到下一个控制点的曲率变化值最小的方向；一种是全局最优，路径方向为所有控制点到下一个控制点的曲率变化值之和最小的方向。全局最优法需要计算所有可能的抛光路径，计算量随着控制点数的增加会急速增长，而局部最优法只需要在当前控制点处作下一步的最优选择，计算量相对全局最优法小很多。除曲率变化最小的要求外，路径规划还必须要达到以下的条件：

1) 遍历全部控制点，要实现复杂曲面MRF抛光时的精确修形，需要去除函数可以对复杂曲面面形误差进行精确去除，因此规划的路径要尽量多包含控制节点。

2) 路径规划时每个控制点只用一次，否则会造成抛光轨迹叠加，导致材料去除不确定。

3) 规划的路径要满足机床动态性能要求，否则无法进行实际加工。

对第1节中的复杂曲面镜面进行离散后，产生m×n阶控制节点，抛光轨迹规划算法如图6所示，步骤如下：

步骤1设置起点p(x,y)，将该点置于已规划点列表中。

步骤2分析下一点，限定路径平行坐标轴，若此点在已规划点列表中，会造成路径重叠，舍弃；如果不在已规划点列表中，则将该点放入未规划点列表中。

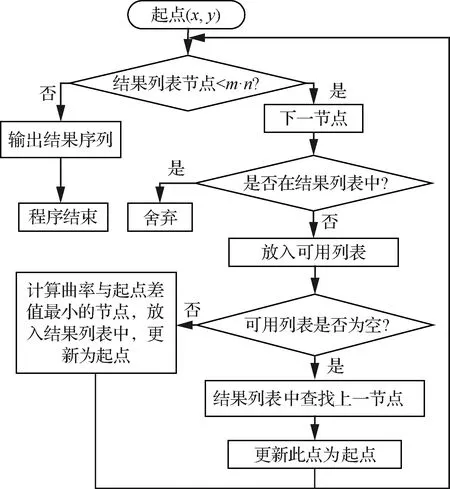
图6 路径优化算法内容与步骤Fig.6 Contents and steps of path optimization algorithm

步骤3判断未规划点列表是否为空集，若是则进行步骤4；若不是则计算未规划点列表中每个点与起点曲率的差值，将最小差值的点放入已规划点列表中，将此点设为新起点，然后执行步骤5。

步骤4若未规划点列表为空集，返回已规划点列表中的上一点，将此点设置为当前起点，返回执行步骤3。

步骤5判断已规划点列表中的点数是否小于m×n， 若是则返回执行步骤3；若不是则输出控制节点坐标，程序结束。

使用一复杂曲面对上述算法进行仿真，此复杂曲面的曲率分布如图7(a)所示，离散后的面形控制点矩阵为8×8阶。对上述算法进行路径规划仿真，所得结果如图7(b)所示。分别计算得到的优化路径、横向线性扫描路径与纵向线性扫描路径3种路径的全局变化率和局部最大相对曲率变化率，其对比结果如表2所示。

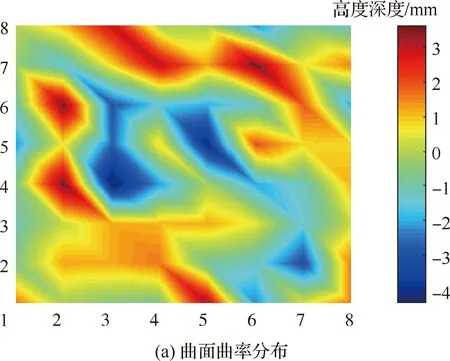
图7 曲面曲率分布及规划得到的优化路径Fig.7 Surface curvature distribution and optimized path obtained by planning

从表2的结论可以分析得出，该路径规划算法的全局变化率小于光栅扫描的全局变化率，但局部最大相对曲率变化率与线性扫描的大致相等，说明没有实现局部曲率变化最小，且此算法在高阶时的运算量比较大，会对计算速度造成不利影响，仍需对其进行优化。

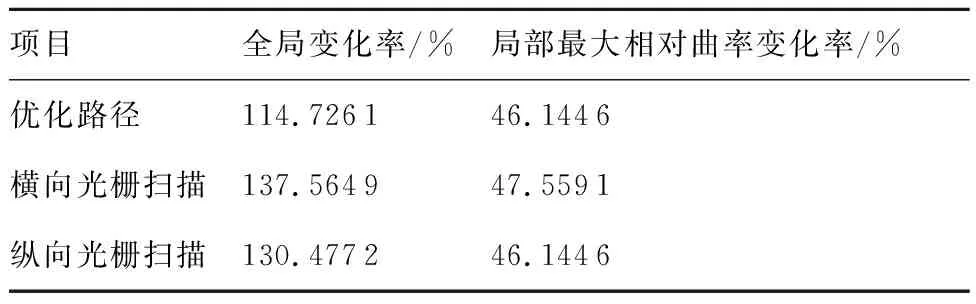
表2 不同路径规划结果指标分析Table 2 Index analysis of different path planning results

2.2 算法优化

由2.1节中的仿真结果可以得出，数据量过大时计算速度会变慢，有时甚至会出现不收敛的情况，因此需要对该路径算法进行优化。2.1节中的路径规划算法，其计算原理是取值到第n点控制点时，根据判断条件选择是否有符合要求的下一点n+1。当这个n+1点存在时，则认为第n点为有效点；若没有符合条件的n+1点时，则认为第n点为无效点，返回上一步。然而，当n点为有效点时，也可能出现后续点无论怎么选择，此条路径都不能满足约束条件的情况。路径规划中的无效点无法形成完整的进出通路，主要有2种类型，第1种为被已经规划过的点和边界包围的点，如图8所示边缘处点Ⅰ；第2种为周围被已规划点包围的点，如图8所示的点Ⅱ。

图8 困点类型示意图Fig.8 Diagram of difficulty point type

上述分析提出的优化方法，其核心在于对第n点进行判断时，先分析n点是否是以上2种类型的无效点，如果是则直接断定n+1点无效，如果不是则按照2.1中的算法继续进行。使用该优化方法对2.1节中的样例进行重新规划计算，在得到同样结果的情况下，运算时间能够节约1/3。

3 磁流变抛光试验

对经过SPDT超精密车削后的复杂曲面铝反射镜进行磁流变抛光试验。该复杂曲面铝反射镜的形状为方形，外形尺寸为59 mm×85 mm，材料为Al-6061铝合金，复杂曲面面形由式(13)表示：

C1x+C2y+C3x2+C4xy+C5y2+

C6x3+C7x2y+C8xy2+C9y3+C10x4+

C11x3y+C12x2y2+C13xy3+C14y4

(13)

式中：C1～C14为面形参数。

图9(a)是根据反射镜镜面形式(13)及各参数的值所绘制的该反射镜的面形三维图，通过最小二乘法拟合得到曲面局部最接近球面曲率半径分布，如图9(b)所示。在相同工件材料相同工况下使用实验法得到平面去除函数，如图9(c)所示，然后利用第2节介绍的路径规划算法得到曲率变化最小的磁流变抛光路径如图9(d)所示。

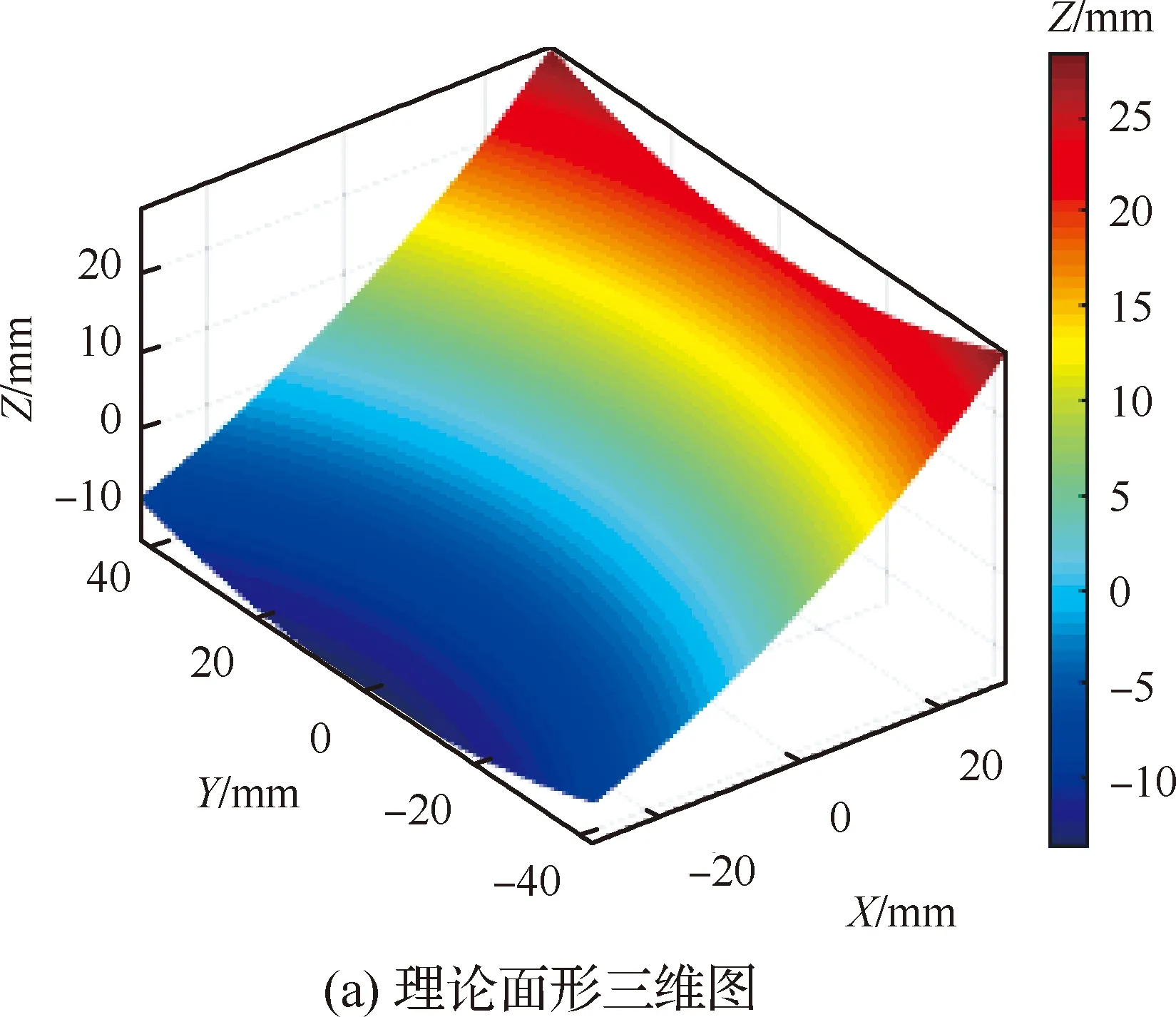
图9 复杂曲面铝反射镜加工前分析Fig.9 Analysis before processing of complex curved aluminum mirror

根据以上分析，设计了复杂曲面铝反射镜的加工工艺路线，如图10所示。与传统的MRF抛光工艺相比，此工艺的优势在于保证了加工过程中去除函数的准确性，因此能够提高加工精度。使用本单位自行研制的磁流变抛光机床对此复杂曲面铝反射镜进行MRF抛光加工，抛光所用的工艺参数如表3所示，抛光机床如图11 所示。

图10 复杂曲面铝反射镜磁流变抛光工艺路线Fig.10 Magnetorheological finishing process of complex curved surface aluminum mirror

表3 抛光工艺参数Table 3 Polishing process parameters

图11 复杂曲面铝反射镜磁流变抛光Fig.11 Magnetorheological finishing of aluminum mirror with complex curved surface

经过2次迭代加工，用时大约70 min，反射镜的面形误差从SPDT超精密车削后的0.687λ PV、0.136λ RMS收敛到0.216λ PV、0.033λ RMS，如图12所示。从图13可以看出，通过MRF磁流变加工后，铝反射镜上SPDT车削后产生的周期性刀纹已完全消失。为了进一步提高镜面表面质量，对MRF加工后的铝反射镜进行了保形光顺加工，最终得到的实物如图14所示。

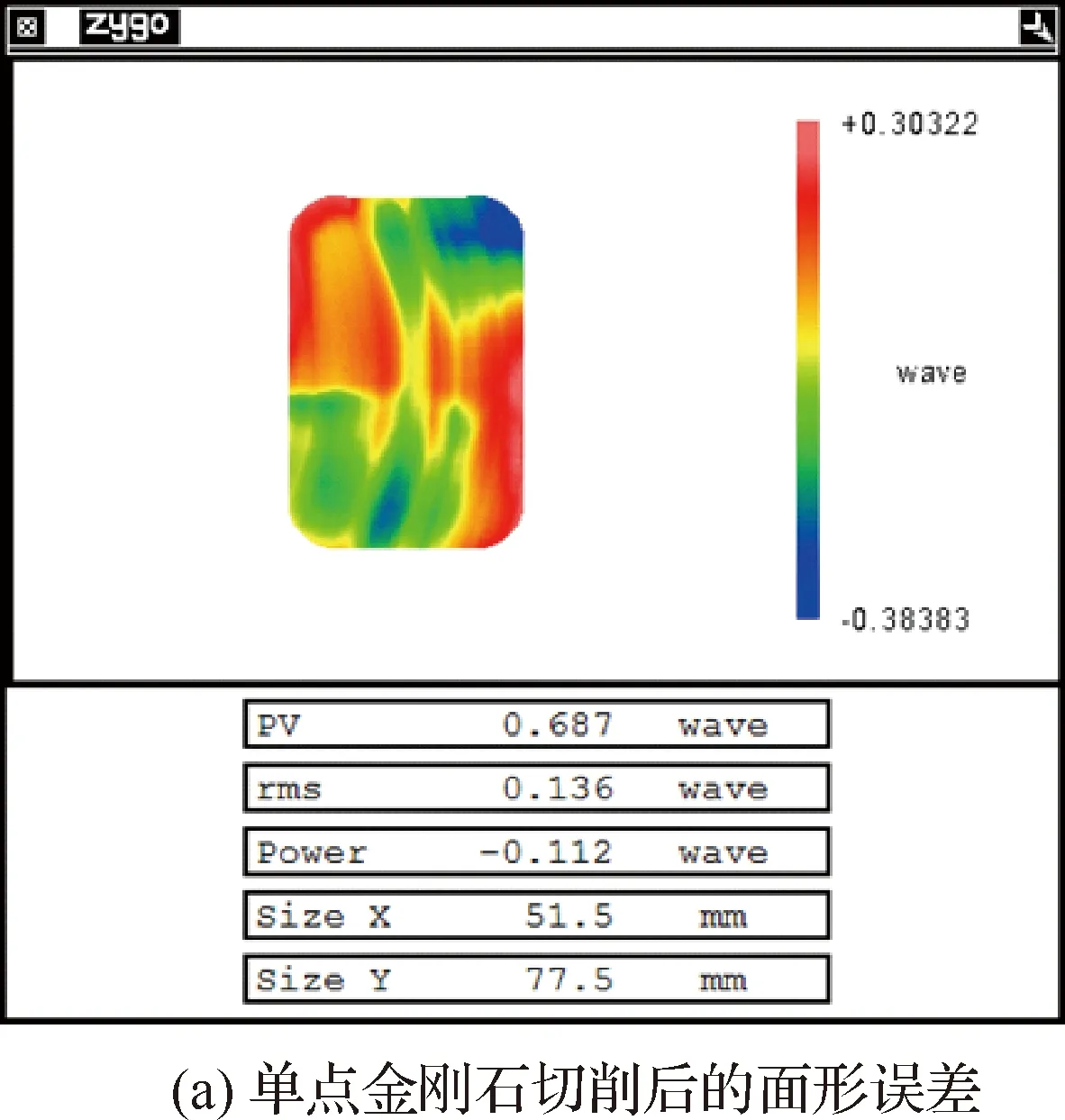
图12 铝反射镜磁流变抛光前后面形误差Fig.12 Shape error of aluminum mirror before and after MRF

图13 铝反射镜磁流变抛光前后微观形貌Fig.13 Microstructure of aluminum mirror before and after MRF

图14 加工完成的复杂曲面铝反射镜Fig.14 Aluminum mirror with complex curved surface after machining

2018年，德国夫琅禾费应用光学与精密工程研究所(Fraunhofer Institute for Applied Optics and Precision Engineering)为位于智利的超大型望远镜中的低温高分辨率红外阶梯摄谱仪加工的平面和球面铝反射镜，采用SPDT超精密车削后使用MRF磁流变抛光的加工流程。该摄谱仪中的M1镜尺寸为78 mm×52 mm，所得的最终面形误差为109.541 nm PV，15.306 nm RMS；M3镜尺寸为115 mm×70 mm，所得的最终面形误差为462.528 nm PV，26.477 nm RMS[23]。目前，国外在磁流变抛光设备、磁流变抛光液与磁流变抛光工艺上对中国均处于封锁状态，本单位的磁流变抛光设备、磁流变抛光液与磁流变抛光工艺均为自行独立研发，其相关成果已达到国际先进水平。

4 结 论

复杂曲面铝反射镜具有优异的结构性能和光学性能，在诸多领域的应用中具有不可替代的作用，已成为光学系统反射镜的重要发展方向之一。但复杂曲面铝反射镜的高精度高质量制造还存在许多尚未解决的难题，作为一种确定性抛光技术，磁流变抛光能够适用于光学复杂曲面的加工，在复杂曲面铝反射镜的超精密加工中具有广阔的发展空间。本文从高精度复杂曲面铝反射镜的应用需求出发，设计了基于磁流变抛光的复杂曲面铝反射镜加工工艺路线，为复杂曲面铝反射镜的超精密加工提供技术支持。

1) 分析了在复杂曲面面形下，曲率变化对磁流变抛光去除函数产生的不利影响，提出了复杂曲面局部区域去除函数的动态建模方法，给出了复杂曲面磁流变抛光去除函数驻留时间的求解算法。

2) 基于曲率变化最小原则，对复杂曲面铝反射镜磁流变抛光路径进行了优化。

3) 制定了复杂曲面铝反射镜抛光的工艺路线，并进行了加工试验，抛光的反射镜的面形误差从SPDT超精密车削后的0.687λPV、0.136λRMS收敛到0.216λPV、0.033λRMS。