基于平衡向量的刚架结构极限承载力分析的广义塑性铰法
2021-12-01杨绿峰殷玉琪柏大炼
杨绿峰,殷玉琪,柏大炼
(1.广西大学土木建筑工程学院,广西,南宁 530004;2.工程防灾与结构安全教育部重点实验室,广西,南宁 530004)
刚架结构由于受力合理、自重轻及结构简单等优点,广泛应用于各工业建筑、民用建筑和交通水利工程等领域中,正确分析刚架结构极限承载力是开展刚架设计和安全性评估的基础。现阶段,主要利用弹塑性理论进行刚架结构失效模式和极限承载力分析,分为塑性区法和塑性铰法。塑性区法[1−2]主要通过细密网格将刚架离散为数量众多的实体单元,并在加载中及时更改进入塑性的单元本构方程,可以精细模拟结构加载时的失效过程,但离散自由度庞大。因此通常采用梁单元建立有限元模型并开展弹塑性增量分析(elasticplastic incremental analysis,EPIA)[3 −4]。塑性区法和EPIA都能取得较高计算精度,其结果往往用于校核其他方法的精度和适用性,但是理论复杂,且非线性迭代分析导致计算耗时久。
传统塑性铰法(plastic hinge method,PHM)采用零长度塑性铰假定,并通过在单元/构件的失效截面添加塑性铰来集中体现材料的塑性行为,单元/构件的其余部分仍保持弹性。而且,在建立有限元模型时仅需将各个构件离散为1个~2个单元,因此与塑性区法相比能够大幅提升计算效率。同时,由于刚架结构往往以弯曲变形为主,传统PHM[5−7]根据外荷载与线弹性弯矩之间的比例关系直接确定结构中新增塑性铰的位置以及相应的荷载增量(该特性称为PHM的比例特性),理论简单,计算格式简洁,计算效率远高于EPIA。但是,研究表明,处于多内力组合作用下的刚架结构,弯矩和轴力是影响其极限承载力的两个主要内力,而传统PHM由于无法考虑轴力对塑性铰的影响将导致高估刚架的极限承载力。二阶塑性铰法[8](second-order plastic hinge method,SPHM)和精细塑性铰法[9](refined plastic hinge method,RPHM)利用广义屈服准则考虑弯矩和轴力对塑性铰的影响,从而克服了传统PHM的缺陷。但是,由于常规的广义屈服函数通常不满足比例条件,导致SPHM和RPHM无法利用传统PHM的比例特性直接确定塑性铰位置和荷载增量,需进行大量的增量非线性迭代分析来确定组合内力下刚架结构在每一加载步下的新增塑性铰位置和荷载增量,导致理论复杂且难度大,降低了计算效率。
为了建立既适用于多内力组合作用的刚架结构,且能够保持PHM的比例特性,Rahman[10]利用线性函数代替非线性的广义屈服函数,据此对截面抗弯强度进行修正,因而能够利用传统PHM的比例特性快捷计算船舶横向框架在多内力作用下的极限承载力。但是,利用线性函数模拟非线性广义屈服函数将影响到极限承载力的计算精度。为此,杨绿峰等[11]利用非线性齐次拟合传统的非线性、非齐次广义屈服函数,并利用齐次广义屈服函数(homogeneous generalized yield function,HGYF)定义单元承载比[12−13],进而根据外荷载与单元承载比之间的比例关系直接确定广义塑性铰的位置和荷载增量,由此建立了广义塑性铰 法(generalized plastic hinge method,GPHM),不仅保持了传统PHM的比例特性,具有很高的计算效率,还进一步提升了PHM在多内力组合作用下的计算精度,有效扩大了PHM的应用范围。但是,GPHM没有考虑荷载增量对前序塑性铰平衡状态的影响,导致刚架结构在部分荷载工况下的承载力计算结果不准确。
针对该问题,本文利用广义屈服条件和转角位移方程建立平衡向量,据此建立修正的GPHM计算格式,解决了GPHM在部分荷载工况下不适用的问题。最后,通过与不同方法对比分析,验证了本文方法高效、高精度的特性。
1 广义塑性铰
1.1 截面修正强度
塑性铰法通常利用上一加载步的内力修正刚架各构件的截面强度[7]:


图1 圆管截面的几何参数Fig.1 Geometric parameters of tube section
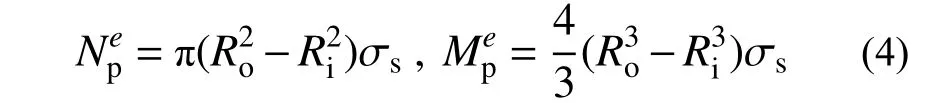
式中:Ro为圆管截面外半径;Ri为圆管截面内半径;σs为材料屈服强度。
1.2 强度折减因子的定义
研究表明,当构件能够满足抗剪承载力要求时,弯矩和轴力将是影响构件承载力失效的关键因素。当刚架中某一构件截面上的弯矩和轴力满足广义屈服准则 f(ni,mi)=1时,该截面进入全截面塑性屈服状态,形成广义塑性铰,其中的f=f(ni,mi)表示广义屈服函数。Chen和Han[14]给出了图1所示圆管截面的广义屈服准则:

式中, f(ni,mi)为圆管截面的广(义屈)服函数,且:
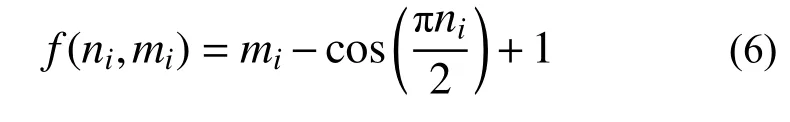
式中,ni和mi分别为刚架在第 i 加载步时构件截面上的无量纲轴力和无量纲弯矩:

利用广义屈服函数可以定义式(1)和式(2)中的强度折减因子ζiN和ζiM。结构中部分构件仅承受单一内力作用,此类构件的强度折减因子为1,但实际工程结构的大多数构件往往都受到轴力、弯矩等多内力的组合作用,此时ζiN和ζiM均小于1。此外,刚架在第一加载步( i =1)之初尚没有累积内力,即: N=M=0,不需要修正单元截面强度,因而有:ζiN=ζiM=1 。随后的加载步(当i>1时),需根据刚架在上一个(第 i−1个)加载步结束时的累积内力确定各个单元的无量纲累积轴力na,i和弯矩 ma,i:

加载过程中需要及时修正构件的截面强度。在修正截面抗弯强度时,应根据广义屈服准则确定累积轴力对截面初始抗弯强度的影响:

式中:g1为广义屈服函数中仅含有轴力的函数项;g2为广义屈服函数中仅含有弯矩的函数项。
将式(7)右式代入式(9),经整理可得:

式中,强度折减因子 ζiM=g[1−g1(n)]表示累积轴力n对单元截面抗弯强度的影响。结合圆管截面的广义屈服函数式(6)容易求得:
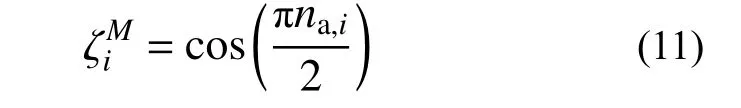
同理,可得轴向强度的折减因子:

1.3 齐次广义屈服函数与单元承载比
从式(6)可以看出,广义屈服函数f 是关于ni和mi的非线性、非齐次方程,与外荷载之间不满足比例条件。杨绿峰等[12−13]提出广义屈服函数齐次化方法,解决了高阶非齐次函数不满足比例条件的难题。这里建立圆管截面的齐次化广义屈服函数。首先针对式(6)的 f(ni,mi),在广义屈服面上建立齐次化表达式 f¯(ni,mi):

式中:ak为多项式待定系数;H为多项式阶数。
为了使齐次广义屈服函数能够更好地拟合广义屈服面,应按照以下方法选择配点。
1)确定无量纲化内力ni和mi的配点。首先,确定ni和mi的取值范围,两者均为[0,1]。然后,在确定区间[0,1]上确定n的i配点:在区间[0,0.1]和[0.9,1]上以0.01为步长均匀布置ni的配点,在区间[0.1,0.9]以0.05为步长均匀布置ni的配点。进而,将ni的配点取值代入广义屈服面式(5)可以确定mi在相应配点上的值。删去其中重复的配点,最终遴选37组配点( ni,mi)(j),j=1,2,···,37。
2)根据选取的配点,利用最小二乘法求得式(13)中不同阶次齐次广义屈服函数(ni,mi)的待定系数ak,进而求得不同阶次ni,mi)的均方根误差,如表1所示。表中可以看出,取 H=4时得到的圆管截面四阶齐次广义屈服函数(ni,mi)能够较好地拟合原广义屈服函数 f(ni,mi),且有:
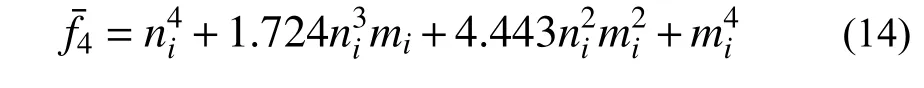

表1 待定系数及均方根误差Table1 Undetermined coefficients and mean-square error
据此,可以定义单元 e 的单元承载比[12-13]:

式中,rie称为单元承载比。rie在单元 e 不同截面上通常有不同的值,这里取其中的最大值。
1.4 塑性铰与荷载增量的确定
对于理想弹塑性刚架结构,外荷载可以用向量表示:
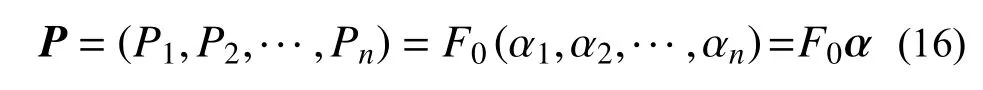
式中:α为基准荷载向量;F0为荷载乘子的初始值;荷载分量 Pk=F0αk(k=1,2,···,n),n为结构承受的荷载数;为了便于表述,通常用荷载乘子F0代表外荷载P。

2 平衡向量与荷载增量的修正
2.1 塑性铰新增内力
根据式(17)容易求得当前加载步的荷载增量FL,i及其在前序加载阶段形成的塑性铰(简称为前序塑性铰)上产生的轴力增量,但塑性铰上的弯矩增量为0。此时需要判别每个前序塑性铰上的新增轴力是否满足式(5)、式(6)定义的广义屈服条件:
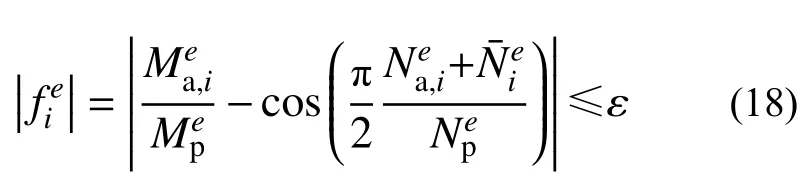
式中,ε为收敛容差,取值范围为0.001~0.01,本文取0.007。
如果全部前序塑性铰上的新增内力相对较小,都能够满足式(18),则将新增内力加入累积内力中,并进入下一个加载步。否则,如果某一前序塑性铰上较大,不满足式(18),表明当前加载步的内力分布尚不满足屈服条件,则需要在全部前序塑性铰上增添附加弯矩,使得:
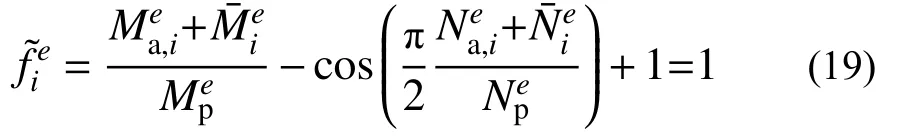
据此可得:


图2 梁-柱单元Fig.2 Beam-column element

单元 e 两端截面上的新增内力和相应的位移如图2(a)所示,应满足转角位移方程:式中:上标A、B分别表示单元e 的左、右端截面;下标 i 表示第 i 加载步。若已知单元 e的左端新增弯矩,A,根据式(21)的前两式可确定单元右端的新增弯矩
,B:

由此,可将式(21)的转角位移方程修改为:
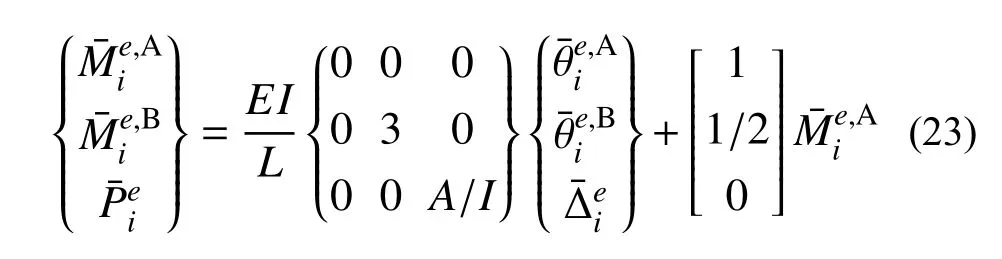
2.2 平衡向量
根据图2所示的两类自由度之间的对应关系,可将式(23)转换表达为有限元法符号约定下的单元刚度方程[10]:
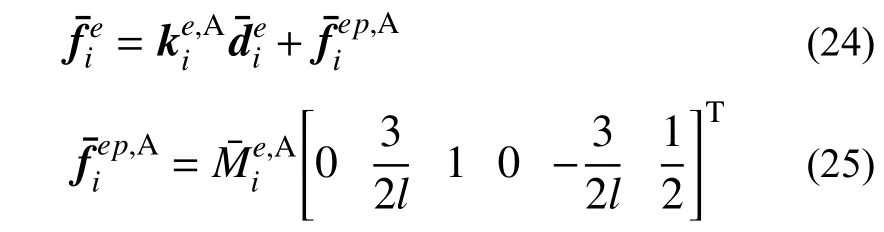

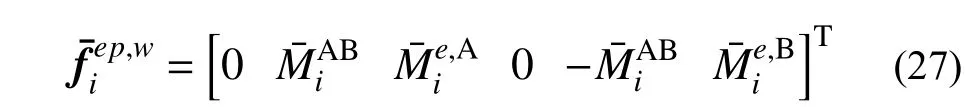
将结构中全部单元刚度方程集成为结构总体刚度方程:

式中,Ki、、和为第 i 加载步末的结构总体刚度矩阵、结点位移向量、等效结点荷载向量和平衡向量,其中的可根据第 i加载步末的外荷载 FL,iα得到。
通过引入平衡向量并开展有限元法再分析,可以消除轴力增量导致的结构内力失衡现象,从而满足式(18)。进而,将ax所在截面(结点)改为塑性铰,并进入下一加载步分析。
3 结构失效路径和极限承载力
根据当前加载步出现的塑性铰位置,修改与该塑性铰相连接的单元刚度矩阵,集成新的结构总体刚度矩阵,并判断其是否奇异。如果非奇异,则进入下一加载步,并重复上述计算步骤,形成新的塑性铰。反之,如果奇异,表明结构达到极限状态,并成为失效机构,结束加载。
在结构加载过程中依次出现的塑性铰构成刚架结构的失效路径。累加各个加载步的荷载增量FL,i可得刚架结构的极限承载力FL:

式中,NL为总的加载步。
上述方法首先利用强度折减因子和广义屈服准则确定塑性铰位置和相应的荷载增量,进而形成平衡向量,据此修正塑性铰位置和荷载增量,最终确定刚架结构失效模式和极限承载力,具体的计算流程见图3。
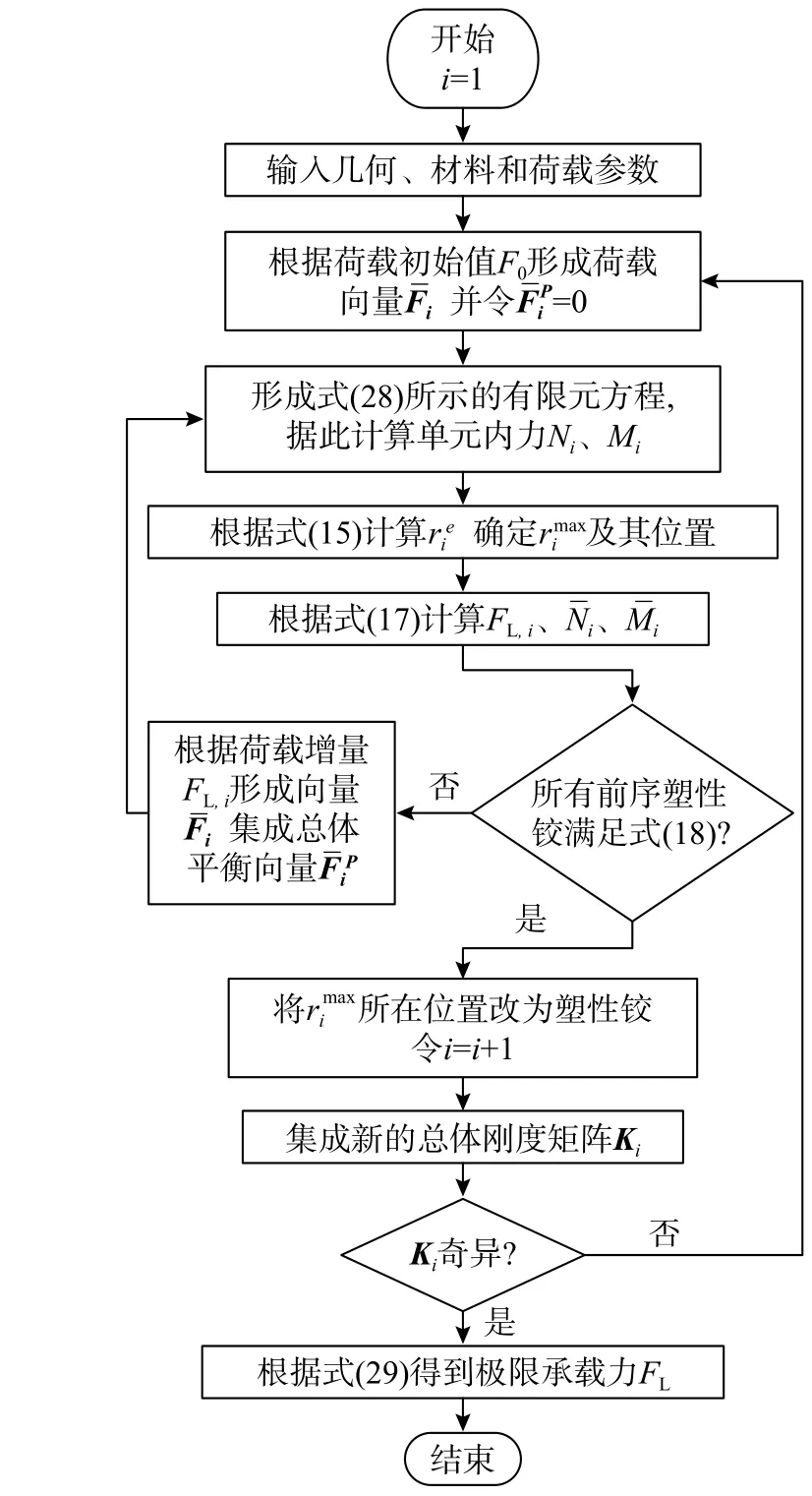
图3 修正的GPHM流程图Fig.3 Flow chart of modified GPHM
上述计算步骤称为修正的GPHM,是对文献[11]建立方法的改进。
4 算例分析
这里利用不同方法计算圆管截面刚架结构的极限承载力,并以弹塑性增量分析方法(EPIA)的计算结果为基准,将本文基于平衡向量的修正GPHM(以下简称为本文方法)计算结果同传统PHM和文献[11]的GPHM(以下简记为文献[11]方法)进行对比分析。其中EPIA采用ANSYS编程,并利用BEAM189建立弹塑性有限元模型;而PHM、文献[11]方法和本文方法都采用MATLAB编制线弹性有限元法计算程序。电脑配置CPU@3.00 GHz,内存8.0 G。
4.1 算例1.单层双跨刚架结构
某单层双跨刚架计算简图如图4所示,紧邻黑色圆点的数字表示杆端截面的编号,承受竖向荷载 P1=16F0和水平荷载 P2=αF0,用向量表示为P=(P1,P2)=F0(16,α) ,其中,α为与水平荷载和竖向荷载的比例有关的常数。刚架梁柱等构件采用规格为 φ140mm×10mm的圆管截面,材料屈服应力为 σs=235MPa ,弹性模量E=2.1×105MPa。分别采用本文方法、EPIA、PHM和文献[11]方法计算刚架结构的失效路径和极限承载力。当取 α=1时,上述四种方法的计算结果见表2。

图4 单层双跨刚架计算简图 /mFig.4 Calculation diagram of one-story-two-bay rigid frame
由表2可知,本文方法得到的失效路径与EPIA完全相同。而文献[11]得到的失效路径中,截面4先于截面5发生失效,因而与本文方法和EPIA的结果稍有不同,但三者的失效模式完全相同。而PHM得到的失效路径、失效模式都与EPIA的结果存在显著差异。由此表明,本文方法能够正确反映结构加载过程中塑性发展和内力再分布,而PHM的结果有误。进一步地,可以看出传统PHM与EPIA的相对误差高达99.87%,表明PHM由于仅考虑弯矩对塑性铰的影响,忽略了其余内力的作用,导致严重高估刚架结构极限承载力,且得到错误的失效路径。文献[11]建立的GPHM能够考虑轴力对塑性铰的影响,从而有效降低了误差。本文方法在此基础上进一步通过平衡向量消除了塑性铰上新增轴力对结构平衡状态的影响,能够正确反映加载中结构塑性发展,从而有效提高了计算精度,将GPHM与EPIA之间的相对误差从文献[11]的4.57%降低到现在的0.68%。
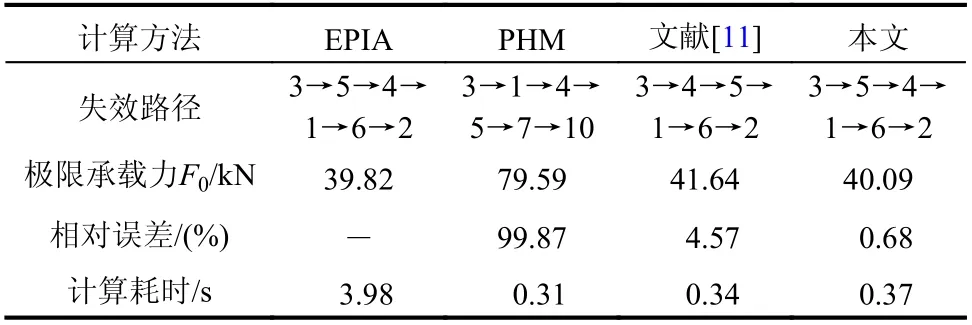
表2 不同方法计算结果Table2 Results from different methods
同时从表2可以看出,本文方法计算耗时仅为EPIA的1/11左右,表明本文方法具有很高的计算效率。进一步地,分析α取不同值时PHM、文献[11]方法和本文方法的计算精度,详见图5。从中可以看出,传统PHM与EPIA的计算结果差距较大,且随着α的减小,两者的相对误差逐渐增大。其原因在于传统PHM不能考虑轴力对塑性铰的贡献,从而高估结构极限承载力,导致较大的计算误差。文献[11]方法尽管能够利用广义屈服准则综合考虑轴力和弯矩的影响,提升了计算精度,但由于没有充分考虑前序塑性铰上新增轴力对结构平衡状态的影响,导致其与EPIA之间存在一定的误差。本文方法在文献[11]基础上,通过引入平衡向量消除前序塑性铰上新增轴力导致结构内力失衡现象,计算结果始终与EPIA吻合较好,验证了本文方法具有较高的计算精度和广泛适用性。

图5 不同α取值下的刚架极限承载力Fig.5 Ultimate bearing capacity of the frame with different α
4.2 算例2.五层三跨刚架结构
如图6所示的五层三跨刚架分别承受水平集中荷载 P1=αF0,竖向集中荷载 P2=8F0,竖向均布荷载 q =F0,构件截面采用薄壁圆管截面,构件截面尺寸及材料参数如表3所示。分别采用本文方法、EPIA、PHM和文献[11]方法计算结构极限承载力并相互对比分析。
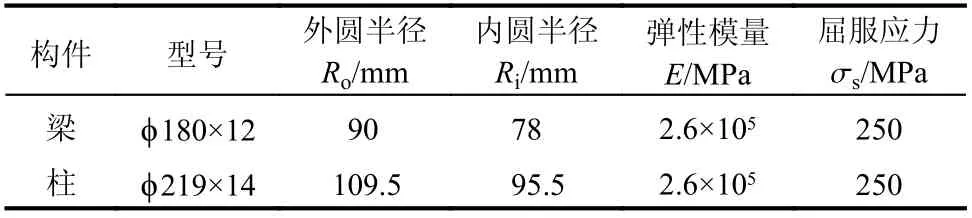
表3 截面尺寸及材料参数Table3 Sectional dimension and material parameters

图6 五层三跨刚架计算简图Fig.6 Sketch of five-story-three-bay rigid frame
当 α=1时,四种方法的计算结果详见表4。由表可知,传统PHM与EPIA的相对误差高达86.3%。再次表明PHM忽略弯矩之外的其余内力对塑性铰的影响,从而严重高估刚架结构极限承载力。文献[11]方法尽管利用广义屈服准则解决了传统PHM难以考虑多内力组合作用影响的问题,在一定程度上提升了计算精度,但由于没有充分考虑塑性铰上新增轴力对塑性铰乃至结构平衡状态的影响,导致其与EPIA之间的相对误差达到14.60%,精度不高。而本文方法在文献[11]的基础上,通过引入平衡向量消除新增轴力对已有塑性铰平衡状态的影响,进一步提升了计算精度,计算结果与EPIA基本吻合,具有较高的计算精度。同时,本文方法计算耗时仅为EPIA的1/58左右,具有很高的计算效率。

表4 运算结果与计算耗时Table4 Computed results and time consuming
进一步地,分别利用EPIA、PHM、文献[11]方法和本文方法计算α取不同值的刚架结构极限承载力,结果如图7所示。从中可以看出,α取值较小时,PHM与文献[11]方法和EPIA的计算结果差距较大,且随着α的增大,两者的计算误差都逐渐缩小。当 α>4时PHM的计算误差不超过7%;当 α>2时文献[11]的计算误差不超过7%。而本文方法计算结果始终与EPIA吻合较好,具有较高的计算精度。
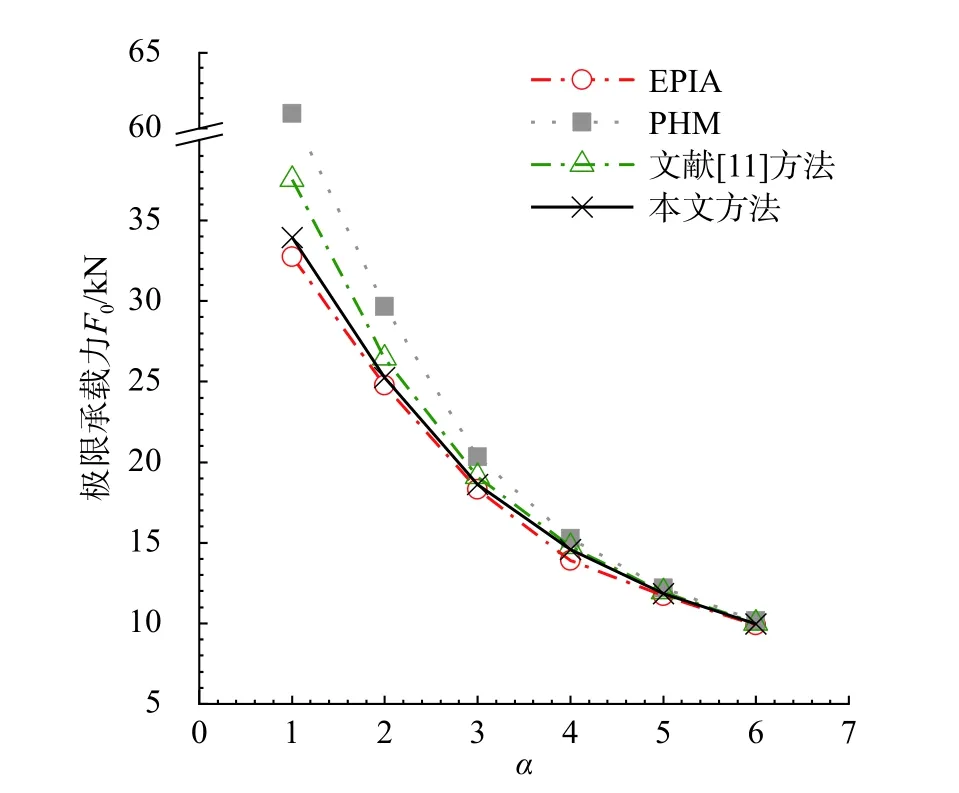
图7 不同α取值下的刚架极限承载力Fig.7 Ultimate bearing capacity of the frame with different α
综上所述,本文方法不仅保持了传统PHM的比例特性,而且克服了传统PHM和文献[11]方法的缺陷,能够取得较高的计算效率和计算精度,且具有较为广泛的适用性。
5 结论
本文利用广义屈服准则和有限元方法建立平衡向量,据此修正了广义塑性铰法的计算格式,并得到如下结论:
(1)弹塑性增量分析法(EPIA)作为结构极限承载力分析的基准方法,具有精度高的优势,但由于采用非线性迭代方法,导致计算效率明显低于各类塑性铰法。
(2)传统塑性铰法(PHM)忽略了轴力对塑性铰的影响,导致过高估算结构极限承载力,影响了计算精度和适用范围。
(3)文献[11]的广义塑性铰法(GPHM)没有考虑加载步荷载增量对前序塑性铰平衡状态的影响,因而应用于承受较大竖向荷载的部分刚架结构时将产生显著误差,不满足工程要求。
(4)本文方法通过引入平衡向量消除了前序塑性铰上新增内力对结构平衡状态的不利影响,从而有效提高了GPHM的计算精度和适用范围。
