节点板式连接对H形钢支撑面外稳定性能的影响

2021-12-01张文元曾立静赵增阳

工程力学 2021年12期

张文元，曾立静，齐欣，赵增阳

(1.哈尔滨工业大学，结构工程灾变与控制教育部重点实验室，黑龙江，哈尔滨 150090；2.哈尔滨工业大学，土木工程智能防灾减灾工业和信息化部重点实验室，黑龙江，哈尔滨 150090)

支撑通过节点板与梁柱连接，构造简单，施工安装方便[1]。相对于支托式连接[2](刚接做法)，板式节点平面内外转动刚度较小，使得支撑寿命更高，结构有更好的耗能能力，更适合于支撑框架结构体系。此连接形式下，节点板对支撑的约束作用不同于铰接和刚接，显示出相对复杂的半刚性节点的特征[3]，故研究节点板式连接对钢支撑面外稳定性能的影响十分必要。

对于板式节点，根据支撑端部的节点板连接净距(以下简称净距)的不同，目前可以分为以下2种形式，如图1所示。第一种是2tg线性净距(tg为节点板厚度)。最早由Astaneh-Asl等[4]提出，要求支撑端部与节点板嵌固点之间保留2tg的距离，来保证支撑先于节点板发生失稳，并且支撑失稳时节点板能够发生面外转动。我国规范[5]亦有此要求。第二种是椭圆净距形式。Lehman等[6]和Roeder等[7]提出即使净距不满足2tg的要求，节点板仍有良好的塑性转动能力，据此给出了该椭圆净距形式。显然，不同的节点板连接形式会对支撑的受压性能产生影响。板式节点作为支撑端部约束，它对支撑稳定性能的影响主要体现在计算长度系数上。美国钢结构设计规范[8]中指出在钢支撑杆件的受压设计时需要合理考虑计算长度系数，但并未针对不同形式的节点连接构造情况给出合理的取值，通常的做法是统一取1.0[9]。我国规范[10,2]的做法类似，即使支撑两端做成刚性连接，计算时仍按铰接计算长度系数1.0来验算支撑压杆的稳定，这种做法较保守。李鸿维[11]通过大规模有限元分析，给出了节点板连接的单斜框架支撑和人字形框架支撑面外计算长度系数取值范围为0.75～0.95。但并未对不同节点板连接形式的支撑计算长度系数给出合理的计算方法，无法指导框架支撑的设计。

图1 支撑端部的节点板连接净距形式Fig.1 Clearance distance types of the gusset plate connection

对于支撑稳定承载力方面的研究，大部分是基于两端铰接约束的支撑构件[12−13]，尚未有节点板连接的支撑构件试验。且支撑构件大多为方形和圆形钢管截面支撑，少有H形截面支撑。于海丰等[14]通过大量的支撑拉压往复循环试验和有限元分析，给出了两端铰接H形支撑的屈曲后承载力计算经验公式，并得出支撑的屈曲后承载力受支撑板件宽厚比影响甚微，主要与长细比有关。从Zheng等[15]研究结果可以看出，钢支撑的抗压承载能力退化较抗拉严重。Faytarouni等[16]通过研究方钢管支撑断裂模型得出，支撑的稳定和屈曲后承载力在前一两次循环内退化较快，后续循环趋于稳定。对于不同节点板连接形式下的支撑框架的力学性能，张文元等[17]通过对不满足2tg净距的板式连接支撑框架进行推覆试验，得出此条件下节点板低周疲劳寿命仍具有高于支撑寿命的可行性，具有合理的屈服机制。Haddad等[18−19]得出增加节点板厚度会增强节点的转动刚度和对支撑的约束能力，尤其在前两个往复循环中会增加支撑的耗能能力。Asada等[20]在有限元分析中，将板式连接支撑框架中的节点板对支撑的约束作用等效成具有一定转动刚度的弹簧，并证明了此简化模型的准确性。这些研究成果为探究节点板式连接对支撑力学性能的影响提供了基础，但是多为定性研究，尚未得出节点板面外转动刚度的合理计算方法，且少有考虑不同节点板连接形式对支撑稳定承载能力的影响。

考虑以上研究中存在的不足，本文进行了12个带节点板的支撑系统试件的往复循环试验，探讨了板式连接对支撑受压稳定性能的影响，对验算支撑稳定承载力时的强度降低系数和屈曲后承载力计算公式进行了修正。结合416个足尺板式连接支撑系统的有限元分析结果，得到了影响节点板面外转动刚度的关键参数，并给出了板式连接支撑系统中节点板面外转动刚度和支撑计算长度系数的建议公式。

1 试验研究

共设计了12个如图2所示带有节点板的H形支撑系统试件，在250 t MTS电液伺服加载系统上进行轴向拉压循环滞回试验。试件顶部为单方向铰接约束(图2中1～5)，底部为梁-柱约束(图2中11和12)。为了保证试件各部分钢材材料力学性能的一致性，令支撑板件和节点板的板厚相同，均为4 mm。支撑板件和节点板均加工自同一块Q355B钢板，材料参数见表1。所有试件支撑截面相同，均为h×b×tw×tf=88 mm×46 mm×4 mm×4 mm。支撑长度均为L=950 mm。所有试件节点板嵌固边长度均为Lg=170 mm，支撑与节点板连接焊缝长度均为L0=100 mm。试件加载条件为轴向等幅循环位移加载。试验中只改变支撑与节点板的连接净距和加载幅值。为了与我国规范中的2tg线性净距要求在物理描述上保持一致，本文用包含正负值的线性净距(见图2)来表示支撑端部与梁柱的相对位置。试验中净距分为2tg、−2tg、−6tg和−10tg4级，正值表示支撑端部与节点板嵌固点连线之间还有一定距离；负值表示支撑端部已经深入到节点板嵌固点连线之内，即支撑端部更加靠近梁柱，这样节点板尺寸小且节点紧凑，建筑效果更好。加载位移幅值与支撑屈服位移的比值分为6、10和14 共3级，分别对应1.2/100、2/100和2.8/100的层间位移角下支撑的轴向位移。具体的试件测量参数见表2。

表1 Q355B材料参数Table1 Material parameters of Q355B

表2 试件测量参数Table2 Measured parameters of specimens

图2 试件构造示意图Fig.2 Schematic diagram of specimen details

2 试验结果分析

2.1 初始稳定承载力

图3给出了12个试件的轴向承载力(加载力P与全截面屈服力Py的比值)和轴向位移(加载位移δ与屈服位移δy的比值)滞回曲线试验结果。在第一个弹塑性循环中，支撑先发生受压失稳(绕弱轴)，而后受压卸载并逐步进入受拉屈服状态。支撑在循环荷载作用下，反复进入屈曲和屈服状态，受拉和受压承载力均有不同程度的退化。所有试件最终破坏模式均为支撑跨中低周疲劳断裂，但净距较小和加载幅值较大的试件也伴随节点板的支撑端部位置处及节点板与端板焊缝位置处的破坏。图4给出了试件的疲劳破坏试验现象图[21]。

图4 试件的疲劳破坏试验现象图Fig.4 Experimental Phenomenon of fatigue failure

图5给出了净距对支撑初始稳定承载力的影响。由于支撑的初始稳定承载力受：1)焊接残余应力；2)初始缺陷；3)试件与加载仪器的对中误差；4)试件本身由于焊接和螺栓安装造成的几何不完全对称的影响较大，所以图中数据点比较分散，但也大体能看出支撑的初始稳定承载力随着净距的减小有增长的趋势。这是因为净距越小，支撑越深入节点板内部，节点板对支撑的约束作用越大，故提高了支撑的稳定承载力。规范[5]建议板式连接杆件面外计算长度系数为1.0，据其计算的结果均小于试验值，说明将面外计算长度系数取为1.0是偏于保守的。

图5 净距对支撑初始稳定承载力的影响Fig.5 Effect of clearance distance on the initial stability capacity of the brace

2.2 稳定承载力退化准则

图6(a)给出了净距对支撑稳定承载力退化的影响。较小的净距会使支撑靠近梁柱，从而增大节点区域对支撑的约束作用，故减小净距会增大支撑的稳定承载力。从图6(b)可以看出，加载幅值对支撑稳定承载力呈现劣化作用。加载幅值越大，试件越易进入塑性，包辛格效应越明显，从而降低稳定承载力。支撑稳定承载力的退化趋势呈非线性，前10个循环内退化明显，后续循环(支撑发生开裂之前)稳定承载力基本保持不变。

我国规范[5]考虑了循环荷载作用下受压承载力的退化，给出支撑杆件的稳定承载力计算方法如下：

式中：N为支撑的轴向力设计值；Abr为支撑杆件的截面面积；φ为轴心受压构件的稳定系数；ψ为受循环荷载时的强度降低系数；λ和λn为支撑杆件的长细比和正则化长细比；f为钢材强度设计值；γRE为支撑稳定破坏承载力抗震调整系数。此方法计算的循环荷载下承载力的退化只与杆件长细比有关。由试验结果(见图6)可知，稳定承载力的退化与净距和加载幅值有很大关系。净距影响节点板对支撑的约束能力，从而影响计算长度系数µ和长细比λ，而且不同循环圈数应对应不同的强度降低系数。

图6 支撑稳定承载力的退化Fig.6 Degeneration of brace stability capacity

式中：n为循环圈数；δ1/50为框架支撑体系层间位移角达到1/50时该支撑轴向的位移幅值。不同循环圈数下，稳定承载力退化程度存在差别(见图6)，故进行分段考虑。本试验构件在n≤80时受压承载力均为稳定退化阶段，支撑开裂会使受压承载力进入到不稳定退化阶段，故在回归分析中不考虑n＞80的情况。由于稳定退化阶段(图6中n＞10时)受压承载力退化非常缓慢，所以对于疲劳寿命较高的构件，即使支撑翼缘开裂发生在第80个拉压循环之后，也可以用n=80时的受压承载力来对n＞80时的受压承载力进行预估。图7 比较了强度降低系数规范值和建议值。可以看出，规范值ψ存在一定程度的不安全性，尤其是在支撑长细比较大时。本文提出的修正后强度降低系数ψ′考虑了循环历程，为分段函数形式，有潜力应用于支撑杆件的疲劳设计，也可在结构的整体弹塑性分析中为制定支撑滞回模型提供参考依据。图8给出了加载循环历程中的关键时刻(n=2,3,4,5,6,7,8,9,10,20,50,70)对应的稳定承载力的试验值与建议公式计算值的对比结果。建议值均位于1.2倍分散带内，说明了此强度降低系数建议公式的准确性。

图7 强度降低系数规范值和建议值的比较Fig.7 Comparison of strength reduction factors in specification and proposal

图8 稳定承载力的试验值与建议值的比较Fig.8 Comparison of measured and suggested stability capacity

2.3 屈曲后承载力建议取值

屈曲后承载力主要用于人字形支撑被撑横梁的设计，来考虑支撑斜杆受压屈曲后承载力退化和受拉屈服而产生的不平衡力的作用。支撑屈曲后承载力为受压位移达到最大加载幅值时的受压承载力。图9给出了支撑屈曲后承载力的退化过程，减小净距会增加支撑的屈曲后承载力，增大加载幅值会降低屈曲后承载力。图10给出了各国规范对于支撑杆件屈曲后承载力的取值。欧洲[22]和加拿大规范[23]的屈曲后承载力计算值远大于其他国家规范和本文试验值，偏保守。中国[10]、美国[8]和日本(式(5)[24])的屈曲后承载力计算值较为接近且与试验值在Δδ/δy=10的情况下非常相近。但是由于没有考虑长细比(中国和美国)和位移幅值对其的影响，与试验值存在偏差。

图9 支撑屈曲后承载力的退化Fig.9 Degradation of brace post-buckling capacity

图10 屈曲后承载力各国规范值与试验值对比Fig.10 Comparison of post-buckling capacity in experiment and different specifications

在支撑的整个加载历程中，受拉承载力和屈曲后承载力均是不断退化的。图11给出了12个试验试件的拉压承载力差值的退化规律。随着循环的不断增加，二者的差值逐渐减小，在第一循环差值最大。故本文只考虑第一循环的屈曲后承载力，并结合规范，给出如下建议公式：

图11 支撑拉压承载力差值的退化规律Fig.11 Degradation of the difference between tensile and post-buckling capacity

式中，β为构件屈曲后承载力降低系数。δ1/50为框架支撑体系层间位移角达到1/50时该支撑轴向的位移幅值，其值为10δy。Δδ为支撑的设计位移幅值，一般情况下对应层间位移角1/50可取为10δy，如果进行抗震性能化设计，可以依据所使用的弹塑性层间位移角限值按比例换算。图12给出了支撑拉压承载力差值试验值与建议值的对比结果。二者十分接近，均位于1.05倍分散带内。此建议公式考虑了长细比和位移幅值的影响，对于不同地震等级下支撑屈曲后承载力取值和被撑梁承载力设计问题有一定的借鉴意义。

图12 拉压承载力差值的试验值与建议值的比较Fig.12 Comparison of measured and suggested values of the difference between tensile and post-buckling capacity

3 数值模拟分析

3.1 有限元模型

基于ABAQUS程序，采用实体单元对12个板式连接支撑系统进行建模和有限元分析。模型均按照实际尺寸，初始缺陷和加载条件进行模拟。在进行疲劳加载步前，赋予支撑一阶振型(正弦半波)形式的初变形，作为支撑的初始几何缺陷，支撑变形最大位置处的挠度值为δx(见表2)。为了提高计算效率，对模型进行了简化。由于试验加载过程中节点板端板与梁、柱没有发生相对变形，近似于嵌固连接，故在简化模型中将其去掉，只保留支撑、节点板和连接板并将节点板嵌固边设置为固定约束，简化前后的有限元模型如图13所示。

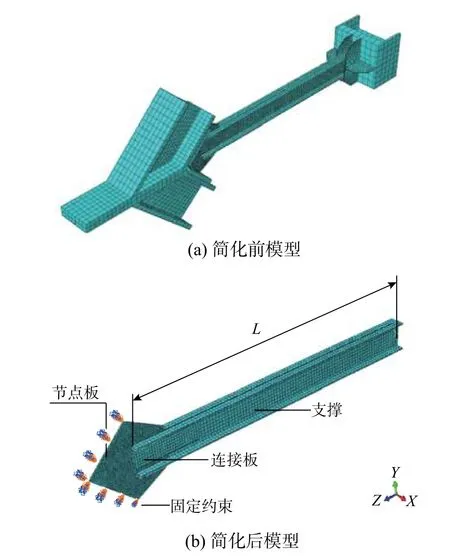
图13 有限元模型Fig.13 Finite element model

图14给出了试件轴向力和轴向位移滞回曲线的模拟值与试验值的对比结果。二者在支撑稳定承载力、屈曲后承载力、屈服承载力、受拉承载力和滞回曲线形状上吻合良好。考虑到本文研究对实际工程的应用性，故不改变构件形态，按照实际工程尺寸建立416个板式连接支撑系统有限元模型(净距−4tg～2tg，支撑轴线与梁轴线夹角40°～55°，支撑长细比60～120和节点板厚度4 mm～50 mm)[25]，为大规模参数化分析提供基础。

图14 GPC-2a滞回曲线模拟值与试验值的比较Fig.14 Comparison of simulated and experimental hysteretic curves

3.2 参数化分析

本文将节点板面外转动刚度r定义为支撑弹性屈曲时的面外转动约束。将节点板的面外约束能力简化为具有相同转动刚度的弹簧[26]，如图15所示。

图15 板式连接杆件稳定承载力求解计算简图Fig.15 The schematic diagram of calculating stability capacity of bracing member with gusset plate connection

按照求解弹性屈曲方程的方法，对于一端铰接一端节点板连接的支撑构件，MA=r1θ，θ =y′(L)，MB=0，r2=0，求解任意截面的微分方程：

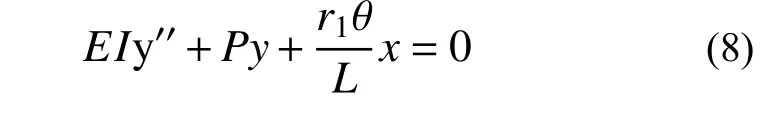
得到r1关于P的表达式：

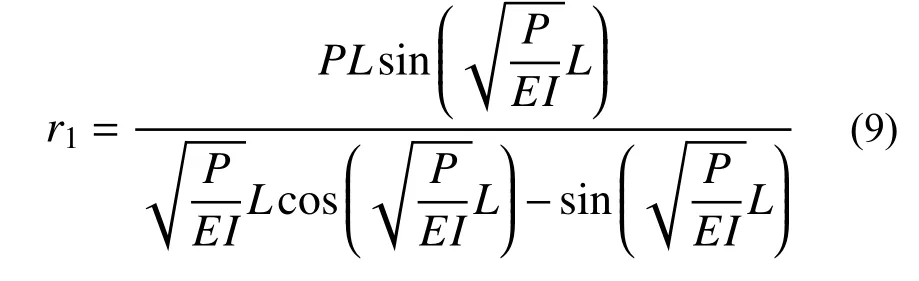
将有限元特征值屈曲分析得到的Pcr代入，即可得到节点板面外转动刚度r1。

图16给出了关键参数对节点板面外转动刚度的影响规律。节点板厚度增加，支撑长细比增加，净距减少均对节点板转动刚度的增加产生近似线性的积极作用。支撑轴线与梁轴线夹角在45°时，节点板转动刚度最小，这是因为此时支撑端部距离节点板嵌固边最远，节点板对其约束能力最弱。节点板转动刚度随支撑角度呈以二次函数形式变化。

图16 主要参数对节点板面外转动刚度的影响规律Fig.16 Effect of main parameters on the out-of-plane rotational stiffness of the gusset plate

3.3 节点板面外转动刚度计算方法

净距和支撑与梁柱夹角确定后，在满足节点强度要求及构造要求(应力扩散角)的基础上，节点板尺寸基本已经确定。结合节点板面外转动刚度的影响因素(见3.2节)并考虑尺寸效应，通过回归拟合，给出节点板面外转动刚度((N·mm)/rad)建议式(10)：

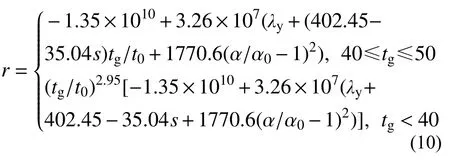
式中：λy为杆件的名义长细比；t0为40 mm；α0为45°；s为净距与节点板厚度的比值。节点板厚度较小时，厚度对节点板面外转动刚度的影响呈指数增长；节点板厚度较大时，厚度将不是节点板面外转动刚度的最主要影响因素，其对节点板面外刚度呈线性增长。

图17给出了416个有限元模型的节点板面外转动刚度基于式(9)的理论值和式(10)的建议值的对比结果。二者十分接近，故建议用式(10)对节点板面外转动刚度进行计算，可靠性强且简单方便。

图17 节点板面外转动刚度理论值与建议值的比较Fig.17 Comparison of theoretical and suggested out-of-plane rotational rigidity of the gusset plate

3.4 支撑计算长度系数建议公式

为了获得支撑的计算长度系数µ，通常需要进行有限元分析和欧拉临界承载力公式得到，缺乏实用性。参考规范[10]中无侧移框架柱的µ与梁柱刚度比的关系，得到板式连接支撑的µ与节点板转动刚度-支撑线刚度比的关系为式(11)。对于一端铰接一端节点板连接的支撑构件r2=0，回归出µ的建议式(12)，如图18所示。当支撑两端均为铰接时，r=0且µ=1；当支撑一端铰接一端嵌固时，r=∞且µ=0.7。

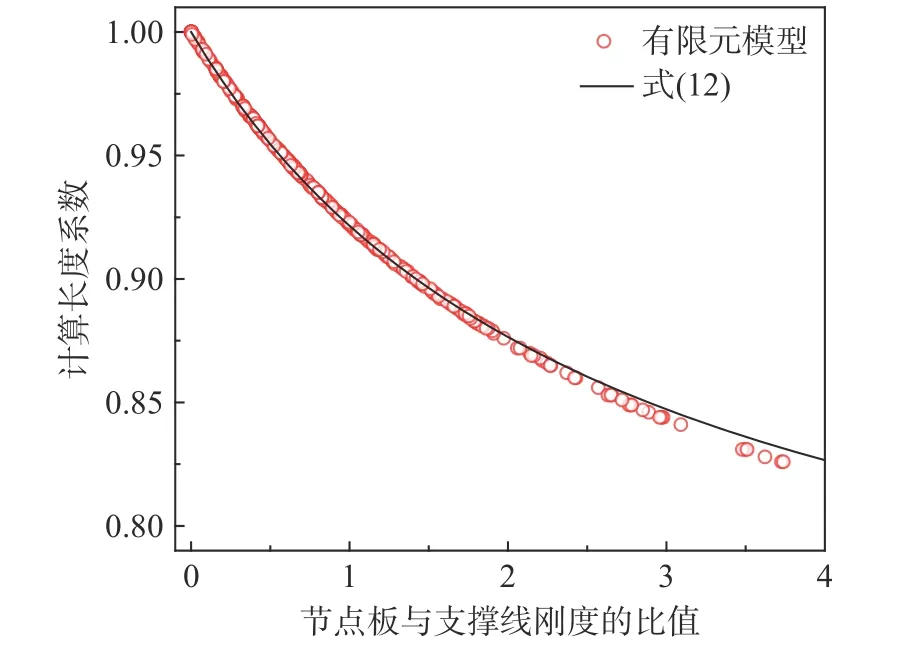
图18 计算长度系数与节点板和支撑线刚度比的关系Fig.18 Relationship between the effective length factor and the rigidity ratio of gusset plate and brace

结合式(10)和式(12)，无需进行有限元模拟，即可获得µ，简单方便。图5给出了此µ建议值下求得的试验试件的初始稳定承载力。与µ=1.0相比，更接近试验值。图19给出了416个有限元模型的µ建议值和利用欧拉临界承载力公式反推出的µ理论值的对比结果。数据点均在1.02倍分散带内，显示出了较好的计算准确度。从该图中也可看出，µ在0.8～1.0范围内。对于支撑两端均为节点板连接的情况，相比于本文中一端铰接一端节点板连接的情况是增强了支撑两端的约束，故而在实际工程中的µ要更小一些。这说明对于板式连接支撑面外计算长度系数，规范中取值为1.0是偏于保守的。支撑两端均为节点板连接的支撑构件的计算长度系数也可按照ω=0.216时的式(11)计算。