基于高斯平滑与模糊函数等高线的雷达辐射源信号分选

2021-12-01侯文太普运伟郭媛蒲马蓝宇

自动化学报 2021年10期

侯文太普运伟郭媛蒲马蓝宇

雷达辐射源信号分选是指从截获的敌方雷达信号中分选出属于单部雷达信号的过程.近年来,随着复杂体制雷达的迅速发展,雷达辐射源信号呈现出了调制方式多样化、波形复杂化、参数快变化的特点.仅利用传统的载波频率(Radio frequence,RF)、到达时间(Time of arrival,TOA)、脉冲宽度(Pulse width,PW)、脉冲幅度(Pulse amplitude,PA)、到达角度(Direction of arrival,DOA) 5 个常规参数进行分选,已难以满足当前战场环境的需求.为此,从新的角度提取更为快捷、有效的脉内特征参数是一种可行方法[1−4].

针对雷达辐射源信号脉内特征参数的提取,已提出Wigner-Hough 变换[5]、双谱分析[6]等多种方法.但这些方法主要针对特定的信号形式,且易受噪声扰动,难于提取分类性能优异的特征参数.文献[7] 结合奇异值分解和分形理论提取了有效的特征参数,但该方法需要分别求解信号的频谱和Choi-Williams 分布(Choi-Williams distribution,CWD),计算复杂度较高.文献[8] 指出,模糊函数(Ambiguity function,AF) 能比较完整地反映信号的内部结构信息,可以挖掘出区别于其他信号的有效特征.文献[9] 以模糊函数主脊(Ambiguity function main ridge,AFMR) 切面为研究对象,提取到了分选效果较好的特征参数.随后,文献[10]利用奇异值分解降噪、文献[11] 利用导数约束平滑对AFMR 进行预处理,进一步加强了AFMR 特征的抗噪性能.

然而,基于AFMR 的AF 特征提取方法的时效性却受限于利用分数自相关或坐标转换计算并搜索AFMR 所增加的运算复杂度.一些学者尝试从新的角度提取AF 特征,文献[12] 提取了AF 的对角线切片为研究对象,然后利用小波分解提取了最优的小波系数作为特征向量.该算法流程简单,但所提特征包含的信息量较少,抗噪性能欠佳.当信噪比(Signal noise ratio,SNR) 下降到0 dB 时信号的平均分选成功率仅为72%.

本文提出一种新的AF 特征提取方法,并将其应用到典型的雷达辐射源信号分选中.首先,计算离散信号的AF 并利用高斯算子进行平滑处理;然后,采用线性插值的方法计算AF 的等高线,再从图像处理的角度提取AF 等高线的正外接矩以及方向角作为特征向量;最后,用核模糊C 均值(Kernelized fuzzy C-means,KFCM) 聚类[13],对特征向量进行分选.本文结构安排如下:第1 节介绍AF 等高线及其计算方法.第2 节给出AF 等高线的正外接矩、方向角提取算法.第3 节利用所提特征和KFCM算法对6 类典型雷达辐射源信号进行了分选,并与现有方法进行了对比.第4 节对本文的研究进行了总结并提出了下一步的研究方向.

1 模糊函数等高线

1.1 模糊函数

对于任意窄带雷达信号s(t),其AF 定义为:

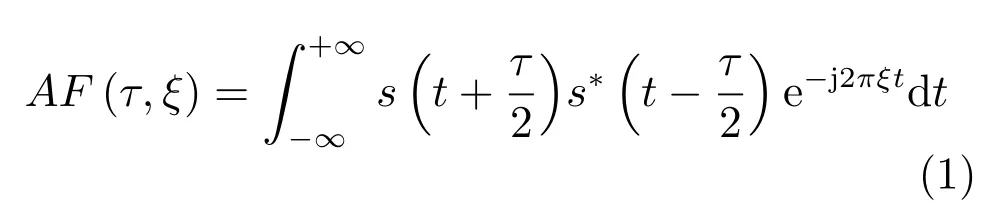
式(1) 中,s∗(t) 为s(t) 的共轭,τ为时延,ξ为频移.可以看出,AF 是信号自相关函数中时间变量t经傅里叶变换后得到的结果[14].AF 唯一性定理指出,信号模糊体积的分配完全取决于信号本身,这为从信号AF 的角度来获取特征参数提供了理论基础.

1.2 模糊函数的高斯平滑处理

实际战场中的雷达信号分选常伴有较强敌方干扰以及背景噪声,使AF 增加了许多毛刺和畸变,增加了分选的难度.考虑到高斯滤波器较好的平滑作用[15],本文构建高斯掩膜对AF 进行平滑处理,即采用某一尺寸的二维零均值高斯掩膜与信号的AF 进行卷积.

1.2.1 构建高斯掩膜

对第i行,j列的任意网格点(i,j) 对应的AF(i,j),其平滑后的AF 为:

式中,w表示网格点(i,j) 的周围M×M大小的掩膜;w(a,b) 为该掩膜内服从二维零均值高斯分布的权重因子,其计算式为:

式中,a,b为权重因子在掩膜中的位置,σ为高斯分布的标准差.

1.2.2 掩膜参数选取

对平滑过程而言,需要控制的参数包含掩膜尺寸M和标准差σ,下面对M和σ的选取依据进行讨论.

高斯掩膜可以看做对连续高斯函数的离散近似,掩膜越大,近似范围越大,但卷积运算中包含的乘法次数也越多.常用的高斯掩膜尺寸有3×3、5×5和7×7,考虑算法复杂度的要求,掩膜尺寸为5×5较为合适,即M=5.

σ决定了掩膜对图像的平滑程度,σ越大,图像越平滑,但图像的细节部分损失也越多,因此σ的选取十分依赖于问题背景.在本文研究中,高斯平滑的作用是校正噪声带来的毛刺与畸变,同时要求同类信号在不同SNR 下的平滑结果接近,以保证后续所提特征的类内聚敛性.本文采用M=5,σ=1 的高斯掩膜分别在0 dB 和20 dB 情况下对常规(CON)信号的AF 进行了平滑处理,结果如图1 所示.由图1(a)、(c) 可以看出,在强噪声干扰下,CON 信号的AF 产生了严重的失真,极大地增加了分选难度.但经过σ=1 的高斯平滑处理后,二者的AF 形状变得接近.其次,由于高斯函数是钟形曲线,µ±2.5σ邻域内的面积占曲线下总面积的98.76%,因此取σ=1 使得5×5 大小的掩膜基本覆盖了整个高斯曲线.综上所述,高斯掩膜的参数选择为M=5,σ=1.

图1 CON 信号的AF 在0 dB 和20 dB 下的平滑效果(σ=1,M=5)Fig.1 Smoothing effect of AF of CON in 20 dB and 0 dB (σ=1,M=5)

1.2.3 模糊函数等高线的计算

由于AF 图是三维的,不利于进行特征提取与分选,因此将AF 图进行降维是十分必要的.AF 的降维需要遵循两个基本原则,一是尽量减少计算量,以保证算法的运算速度;二是降维后的图形能够最大限度地保留AF 的特性.文献[16] 在极坐标域内提取AF 的二维图形轮廓,但这样会增加较大的计算量;文献[17] 分别提取了AF 的主侧视图,但这样时频域的信息无法同时兼顾;结合图1 和AF 的计算式可以看出,AF 是信号的联合时频表示,在三维空间中呈现出了类似山群的地貌形态,因此从地理信息学的角度对AF 的近似方法进行探究是一种可行思路.作为经典的地形分析工具,等高线具有在宏观尺度上揭示地貌对象的群体嵌套、组合关联和空间层次结构特征的功能,在地理空间信息表达中占有主要地位[18−19].因此利用等高线对AF 进行降维,有望提取到分选性能更加优异的特征参数.

AF 等高线的绘制过程中,核心问题在于等高线高度的确定以及所有等值点坐标的求解.由于AF 是以离散网格数据的形式存储在矩阵中,因此可根据高斯平滑后AF 的海拔极差自适应地确定等高线高度并通过线性插值求解无法直接观测的等值点[19],具体步骤如下:

首先根据需要将高斯平滑后AF 的海拔分为P个递增的等高线高度Hp:

根据插值法可得,任意网格(i,j) 在水平方向高度为Hp的等值点坐标(xc,yc) 为:

网格(i,j) 在竖直方向高度为Hp的等值点坐标(xc,yc) 为:

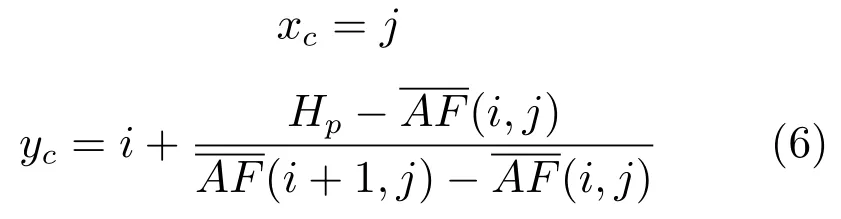
求得等值点坐标后连接相邻的等值点即可得到等高线图.等高线的密集程度取决于P的大小,P越大对地形的描述越详细.但P过大会导致图像不够清晰,并大大增加工作量.通常情况下,绘制三个高度(P=3) 的等高线即可.图2给出了常规(Convention,CON)、线性调频(Linear frequency modulation,LFM)、二相编码(Binary phase shift keying,BPSK)、四相编码(Quadrature phase shift keying,QPSK)、M 伪随机序列(Msequence,MSEQ) 和二频编码(Binary frequency shift keying,BFSK)6 类典型信号的AF 等高线图,图中N为信号采样长度.

图2 6 类典型信号的AF 等高线Fig.2 AF contour lines of six typical signals

2 模糊函数等高线特征提取

目前,图像处理领域中针对图像结构特点的描述已经有了许多可行的方法.例如从全局结构出发提取图像区域面积、位置、方向角,从局部细节出发提取边界曲率、傅里叶描述子、链码描述符等[20−21].在噪声的干扰下,AF 等高线的局部细节可能产生无法预计的塌陷、腐蚀,但自身的基本形状能够得以保持.因此,从AF 等高线的全局结构出发有望提取到分选效果和抗噪性能较好的特征.从图2 可以直观地看出,不同信号的AF 等高线形状不同、分布各异且同样具备原点对称的特性.本节将提取正外接矩和方向角来描述AF 等高线的特点.

2.1 正外接矩

由于正外接矩基本拟合了图形在水平方向和竖直方向的延展范围,因此采用正外接矩特征可有效地反映AF 等高线在时频域的分布状况.本研究中,采用长宽平行于坐标轴的矩形对AF 等高线进行逼近即可求得正外接矩,图3 给出了LFM 信号正外接矩的示意图.

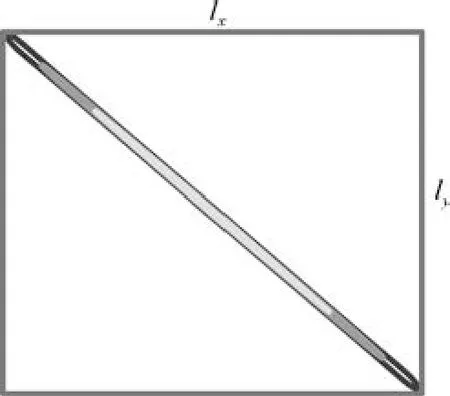
图3 LFM 信号的正外接矩Fig.3 Positive bounding rectangle of LFM

设AF 等值点的坐标为(xc,yc),则AF 等高线的正外接矩长lx、宽ly分别为:

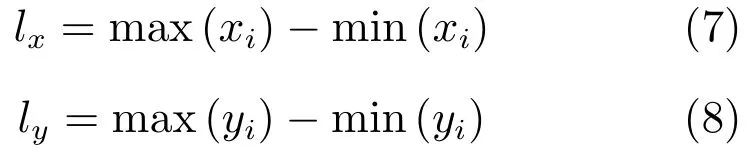
得到AF 等高线的正外接矩后,可采用其面积S和纵横比AR作为分选特征.设正外接矩的长为lx,宽为ly,S与AR的计算式分别为:

2.2 方向角

由AF 的体积不变性定理可知,AF 仅与信号的能量有关,不同的信号形式将以不同的方式分配模糊体积.体积分配不均势必导致其等高线的走向发生偏移,因此可以利用等高线的方向角来表征信号模糊体积的分配特性.定义方向角α为图形主轴与X轴正方向形成的夹角.图4 给出了LFM 信号的方向角示意图.

图4 LFM 信号的方向角Fig.4 Direction angle of LFM

设AF 等高线的轮廓点坐标为(xc,yc),根据AF 等高线的原点对称性,设AF 的右半采样域为δ,α的计算式为:

综上所述,基于高斯平滑与模糊函数等高线的雷达辐射源信号分选算法流程如下所示:

3 仿真实验与结果分析

选取CON、LFM、BPSK、QPSK、MSEQ、BFSK 6 种典型信号进行分选仿真实验,取信号重采样点数N为1 024.其中,LFM 的带宽为10 MHz,BPSK 和BFSK 均采用13 位Barker 码,QPSK采用16 位Frank 码,MSEQ 所用伪随机序列为(1011100).所有信号脉宽均为10µs,除了BFSK信号的两个频点分别取10 MHz 和2 MHz 外,其余信号的载频均为10 MHz.实验所用计算机为微星GE62,CPU 为2.6 GHz,内存为8.0 GB,仿真平台为MATLAB 2015b.

3.1 固定信噪比下的分选实验

SNR 从0∼20 dB 每隔2 dB,每类信号产生100 个不同初相的测试样本,分别组成SNR 固定的11 个600 样本的信号集1,利用本文方法提取各个信号的等高线特征并采用KFCM 算法进行聚类分选.表1 给出了各个SNR 下10 次实验的平均分选成功率.

表1 信号集1 的平均分选成功率(%)Table 1 Average correct rate of signal set1 (%)

算法1.基于高斯平滑与模糊函数等高线的雷达辐射源信号分选算法

1:初始化变量

2:Emitter:待分选的辐射源

3:Num:每个辐射源产生的信号个数

4:SNR:信噪比

5:n:信号长度

6:N:信号重采样长度

7:VVV:特征向量

8:for allEmitterdo

9:for allSNRdo

10:for allNumdo

11:获得离散信号s(n):

12:根据有理式N/n将信号s(n) 重采样为N点:

13:根据式(1) 计算AF:

14:用M=5,σ=1 的高斯掩膜对AF进行平滑处理;

15:采用第1.2.3 节方法求解AF 等高线:

16:根据式 (7)∼(11) 分别计算S,AR,α;

17:构建并保存特征向量V=[S,AR,α]:

18:end for

19:end for

20:end for

21:利用KFCM 算法对V进行聚类分选;

22:统计分选结果.

从表1 可见,CON、LFM 两种信号在0∼20 dB范围内的分选成功率均为100%.结合图2 不难发现,这是因为仅有CON、LFM 信号的等高线呈细棍形且LFM 信号的倾斜角达到了−60◦,因此他们在低SNR 下依然能保持自身特性.其次,由于BFSK信号为二相频率调制信号,当频移经过第二频点时,AF 值达到另一极值.因此BFSK 信号的等高线图除靠近原点的主要分布带之外,BFSK 信号的等高线还有两个独立分布的“小岛”,易于区分.另外,由于BPSK、QPSK 和MSEQ 信号同为非线性调制,其AF 等高线存在部分的交叠,导致它们在4 dB 以下时的分选产生了一定误差.

目前较为热门的深度学习具有强大的数据自学习能力,也是特征表达的可行思路[22].为比较本文方法与深度学习对AF 的特征表达能力,本文利用栈式自动编码机(Stacked autoencoder,SAE),取20∼30 dB 范围内每种信号各10 个总共180 个样本作为训练集,在学习率为0.01、隐含层节点构造为300∼100 的条件下对6 类信号进行分选实验.此外,本文还给出了与文献[6−7]、[9]、[12] 方法的分选正确率对比,详见图5.

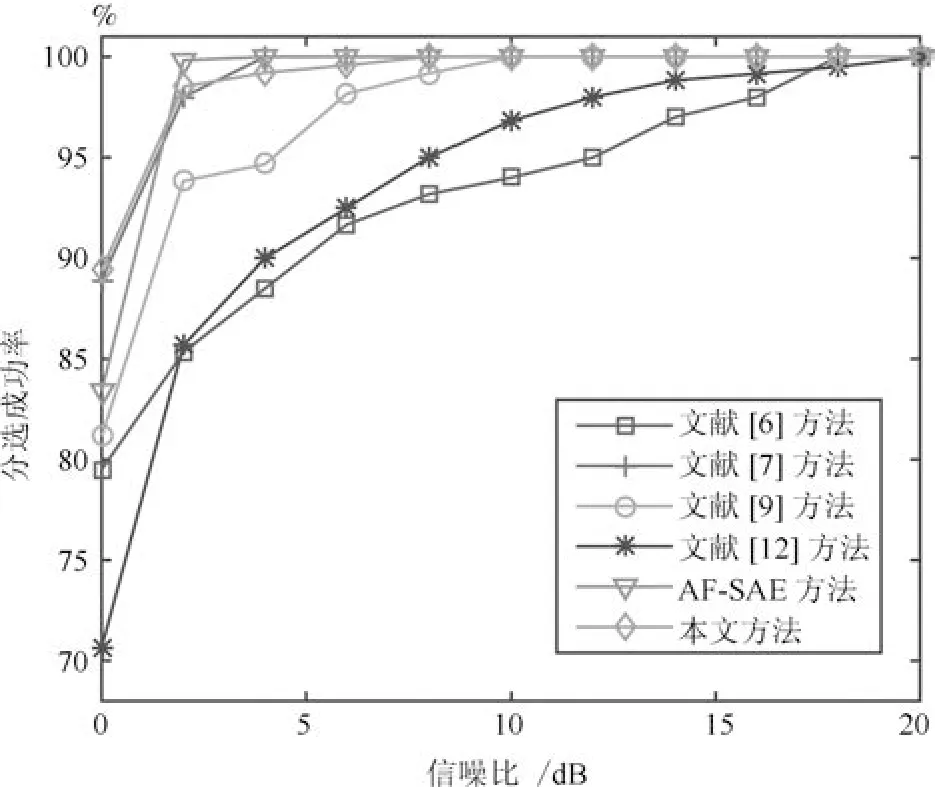
图5 分选成功率对比Fig.5 Comparison of successful rate

图5 可以看出,6 种方法分选6 类信号的成功率随着SNR 的逐渐降低均呈下降趋势.由于双谱特征是对信号的相位噪声特性进行提取,因此文献[6]对不同调制的辐射源分选效果不佳,SNR 下降到16 dB 时便开始产生了误差.文献[7] 提出的奇异熵特征与分形维数特征分别综合了频谱图像与时频图像中的信息,因此该特征反映的脉内信息比较全面,在0 dB 下的分选成功率达到了88.90%,与本文方法基本持平.基于AF 的方法中,AF-SAE 的分选能力在2 dB 以上具有一定优势.但SAE 过度学习了低海拔AF 的信息,而低海拔的AF 极易受噪声影响,因此该方法的分选效果在0 dB 产生了大幅下滑.另外值得注意的是,深度学习需要大量的训练样本,一些低截获概率雷达和新体制雷达并没有大量可训练的数据,对于这类雷达信号的AF,深度学习无法获取到更好的表示方法,因此基于图像处理的AF 降维与特征提取方法依然是当前的研究重点.文献[9] 提取的AFMR 是AF 在整个时频域内搜索到的最大截面,因此AFMR 特征具备较强的抗干扰能力,在0 dB 时平均分选成功率也达到了令人满意的81.16%.文献[12] 的AF 对角线特征的分选成功率从5 dB 开始大幅降低,这是AF 对角线蕴含的信息较少且无法表征AF 的三维分布特性所致.

除AF 主脊外,一些海拔较高的AF 地貌也蕴含着丰富的脉内信息.本文提出的AF 等高线则较好地利用了这部分信息,为AF 的三维地貌特点提供了更为完整地描述.因此等高线特征展现出了比同类方法更强的稳定性,即使在0 dB 下,平均分选成功率也保持在89.04%以上.本实验说明本文特征对信号的AF 具有较强的表达能力且在低SNR 下依然具备良好的类内聚敛性与类间分离度.

3.2 动态信噪比下的分选实验

为验证本文所提特征在SNR 变化时的性能,取0 到20 dB 中每隔2 dB 对每类信号各取10 个随机样本,组成一个660 样本的信号集2.图6 给出了信号集2 的分选效果图,折线相连的点代表分成一类的信号,表2 给出了详细的分选统计数据.

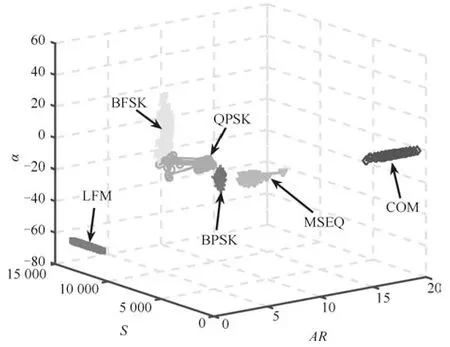
图6 信号集2 的分选效果图Fig.6 Sorting effect diagram of signal set2

从图6 不难看出,在0∼20 dB 动态SNR 环境下,CON、LFM 信号的特征参数分布较为集中且与其他信号相隔较远,展现出了较好的抗噪性能.BPSK 和QPSK 信号的特征参数在SNR 的动态变化下产生了部分交叠,这是由于BPSK 信号和QPSK 信号的主要区别在于相位调制的阶数不同,在强噪声的干扰下频移特性并不是十分显著,导致抗噪性能略有下降.此外,由于0 dB 下约有10%的BFSK 信号的小岛状区域被噪声淹没,导致其等高线的分布范围向QPSK 信号靠拢,使分选产生一定误差.从表2 中可以看出,仅有2.7%的BPSK 和QPSK 信号产生了交叠,3.6%的MSEQ 信号错分到了BPSK,11.8%的BFSK 错分到了QPSK 信号,整体分选成功率达到了96.36%,说明所提特征参数能够适应较大动态SNR 情形.

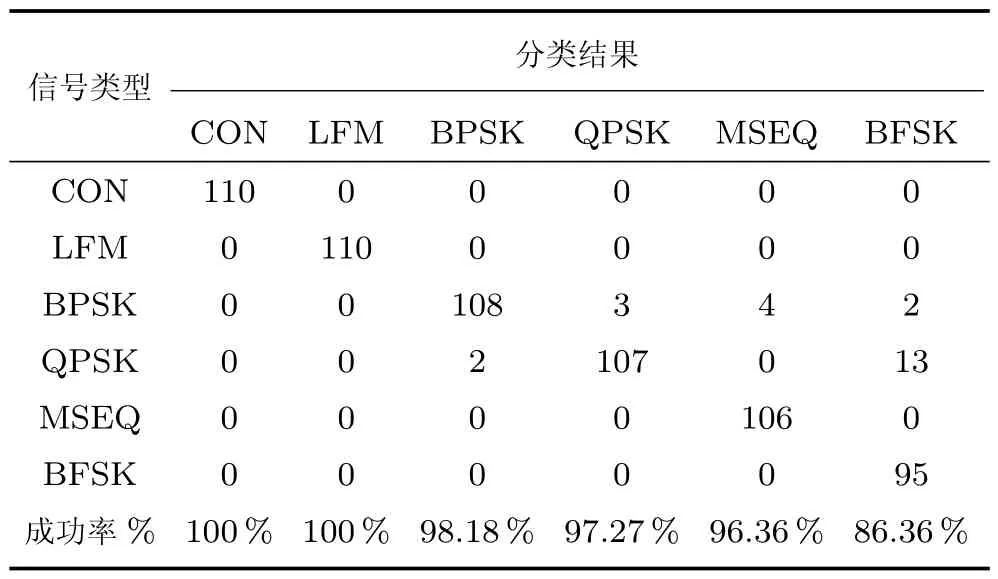
表2 信号集2 的分选结果Table 2 Sorting results of signal set2

3.3 实测雷达数据实验

为了进一步验证本文方法在实际工程中的应用价值,采用雷达外场实测数据进行实验.实测信号集参数如表3 所示.分别使用特征向量V1=[RF,PW] 和V2=[S,AR,α,RF,PW] 进行聚类分选.表4 给出了V1和V2对实测信号集的分选结果对比.

从表3 可以看出,信号集3 中的调制类型、调制参数均有明显的交叠,基本满足复杂电磁环境的要求.表4 实验结果表明,仅采用RF和PW两个参数分选时,3 号辐射源的所有个体均不同程度地混叠到了RF接近的1 号辐射源以及PW接近的5号辐射源中,并未单独形成一类,无法分选.此外,4号、5 号辐射源的参数存在显著跳变,受其影响也较难区分.由于线性调频信号的细棍形等高线明显区别于非线性调制信号的梭形等高线,因此增加本文所提特征后,采用线性调频的5 号辐射源的分选成功率提高到了92%,非线性调制的3 号辐射源的聚类效果也得到了提升,单独形成了一类.本文特征对4 号辐射源分选效果的提升有限,这是因为PW会改变CON 信号AF 的延展范围和频移方向的零点位置,当PW较大时,CON 信号的AF 等高线形状会介于细棍形和梭形之间,导致4 号辐射源的部分信号错分.但总体来说,S、AR、α针对以上几种辐射源的分选都起到了一定增益效果,证明所提特征可作为当前雷达辐射源信号特征参数集的有效补充.

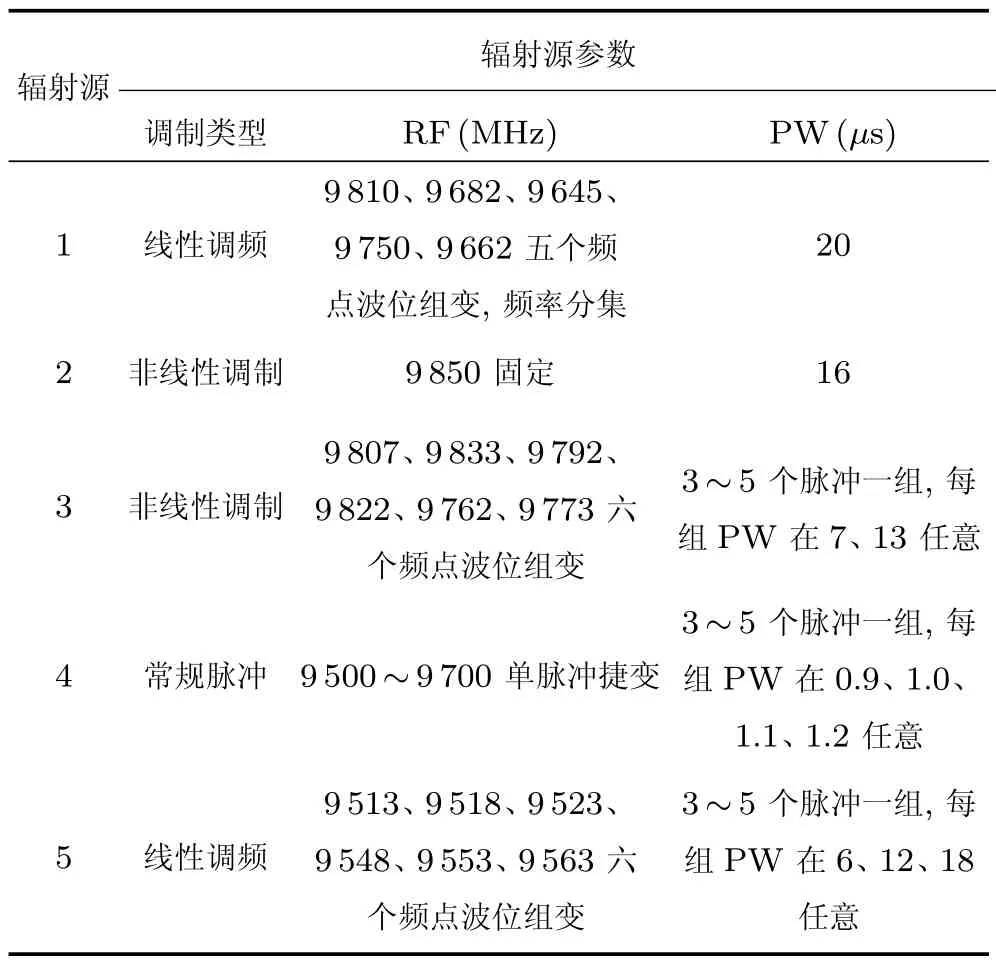
表3 实测雷达数据参数分布Table 3 Distribution of measured radar parameters

表4 实测雷达数据分选结果(%)Table 4 Sorting results of measured radar data (%)

3.4 特征提取耗时对比实验

由于真实战场中会出现大量甚至海量的雷达信号,如果不能快速并有效地识别,将对作战构成巨大的潜在威胁,因此计算复杂度是雷达辐射源信号分选方法的重要指标[4].本实验中,利用MATLAB自带的计时工具tic 和toc 统计本文方法的特征提取耗时,并与文献[6] 所用的双谱特征、文献[7] 所用的奇异熵与分形维数特征、文献[9] 所用的经典AFMR 特征、文献[12] 所用的AF 对角线特征的提取耗时进行比较.表5 给出了各类特征的平均提取耗时统计.

从表5 可以看出,各类特征的提取耗时不尽相同,这也从侧面反映了各类方法计算量的差异.经典AFMR 特征的提取耗时最长,奇异熵和分形维数特征次之.双谱特征、AF 等高线特征以及本文特征的提取耗时较为接近,均为0.2 s 左右,具备较强的时效性.以上方法的问题规模均取决于信号重采样的点数N,因此可根据算法主要语句相对于N的频度和对各类方法的计算量进行分析.

表5 特征提取耗时对比(s)Table 5 Timing comparison of the feature extration (s)

根据文献[6] 中的算法步骤,提取双谱特征首先需计算双谱幅度谱.双谱幅度谱的计算需要进行K(数据分段数) 次FFT 计算,而单次FFT 的复杂度为O(NlogN),因此该环节的算法复杂度为O(KNlogN).其次需计算双谱幅度谱特征截面的分形维数,分形维数包含盒维数与信息维数,该环节复杂度为O(2N),因此双谱特征的复杂度为O(KNlogN+2N).

文献[7] 本质上是对文献[6] 的改进与补充,采用CWD 变换代替双谱作为分形维数的提取对象,其次增加了频谱的奇异熵作为分选特征.奇异值分解包含矩阵相乘运算,复杂度为O(N3).频谱以及CWD 变换可采用FFT 实现,因此该文特征的算法复杂度为O(N3+2NlogN+2N).

文献[9] 中AFMR 特征的提取首先需利用分数自相关计算任意角度对应的AF 值.一次分数自相关运算包含一个1+P阶的分数傅里叶变换和一次傅里叶逆变换(复杂度为O(NlogN)),由文献[24]可知,快速分数傅里叶变换复杂度为O(9NlogN).其次,需要在[−π/2,π/2] 范围内对AFMR 进行搜索,当搜索精度为0.1◦时,搜索次数为1 800 次,因此AFMR 特征的复杂度为O(18 000NlogN).

文献[12] 提取的是AF 对角线的小波系数.由于AF 对角线特征的提取面向网格采样的离散AF 值,可直接用FFT 计算AF,该环节复杂度为O(NlogN).其次需要将AF 对角线进行小波分解,根据文献[23] 的小波快速算法,至少需要2n次FFT 运算,因此该方法的复杂度为O((2n+1)NlogN),其中n为小波分解层数.

本文方法与文献[12] 相同,采用FFT 直接计算网格采样的离散AF 值.高斯平滑环节,先对AF逐行平滑,再对中间结果逐列平滑,算法复杂度为O(2MN2),M为高斯掩膜的尺寸.等高线的求解环节,考虑最坏情况(所有相邻AF 之间均有等值点存在),复杂度为O(3N2).正外接矩与方向角的计算量可忽略,因此本文方法的算法复杂度为O(NlogN+(2M+3)N2).

综合以上分析,从算法阶数来看,文献[7] 提取的奇异熵与分形维数特征复杂度阶数最高,其次是本文特征.文献[6]、[9]、[12] 的复杂度均为O(NlogN) 阶,但常系数有很大不同.实际应用中N的取值通常为100∼1 000,因此可对算法总计算量C进行估算.总计算量的比较结果为:C文献[6]≈C文献[12]