考虑电网调峰需求的工业园区主动配电系统调度学习优化
2021-12-01汤必强
唐 昊 刘 畅 杨 明 汤必强 许 丹 吕 凯
近年来,由于能源危机和生存环境的不断恶化,各国政府纷纷出台政策鼓励和推进新能源发展.随着光伏(Photovoltaic,PV)、风电等新能源的大规模应用,配电网的分布式特性愈发明显,电网调峰形势愈加严峻[1],传统配电网逐渐演变成为可对分布式发电、柔性负荷和储能三者进行主动控制的主动配电系统[2−3].如何有效利用需求响应资源以及对新能源、储能、柔性负荷等分布式调峰资源进行协调优化控制,提高新能源利用率,缓解电网调峰压力,保持配电系统运行的经济性,增强电力系统的可靠性和可控性,是主动配电系统研究的重要发展趋势[4−5].
国内外学者通过不同的建模与求解方法对各类主动配电系统的运行、管理、优化等问题展开了大量研究.文献[6]在考虑分布式能源特性的基础上建立了主动配电系统优化调度模型,并提出了基于智能单粒子优化算法的求解方法,实现完整调度周期内主动配电系统优化调度策略求解.文献[7]建立了分布式电源和储能系统的多目标协调规划模型,并采用了改进的生物地理学优化算法对主动配电系统多目标调度问题进行求解,但以上文献均未考虑到柔性负荷对调度问题的影响.文献[8]建立了考虑分布式能源和柔性负荷的主动配电系统调度规划模型,并提出了一种免疫二叉萤火虫算法来求解多目标优化问题的最优策略,但没有考虑储能装置和柔性负荷的协调调度作用.文献[9]提出一种新的多周期柔性负荷与储能系统协调调度模型,并通过改进的粒子群算法对主动配电系统经济调度问题进行求解.上述文献均是在预测数据的基础上对主动配电系统的运行优化问题进行研究,并未考虑到系统中新能源出力和各类负荷变化过程的随机动态特性对系统运行效率的影响.但新能源出力及各类负荷需求的不确定性是普遍存在且不可避免的,当实际值与日前预测值相差较大时,若以预测数据为基础确定相应的优化控制策略,将难以保证主动配电系统的长期经济运行.
另外,随着新能源渗透率的日益增加以及用电环节的不断智能化,主动配电系统源荷双侧的不确定性不断加大,电力系统调度也不断向智能化发展,传统的基于模型的静态优化算法变得越发不适用[10−11].在智能电网背景下,利用人工智能技术为电力系统动态调度问题提供智能化解决方案是当前调度计划研究的重点[12−13].
目前,主动配电系统的优化研究主要针对居民用户和商业用户,对工业用户的研究较少,且较少考虑需求侧调峰问题[14].为此,储能系统和柔性负荷作为需求侧调峰资源参与电力调度问题越发值得关注.文献[15]提出了一种储能系统削峰填谷的变参数功率差控制方法,实现在满足商业园区运行经济性的同时降低自身负荷峰谷差的目标.文献[16]构建了供需侧联合随机调度模型,并通过仿真验证了柔性负荷的调峰效益.文献[17]论证了对工业园区内的柔性负荷进行控制能够降低用电高峰期用户集中用电给电网带来的调峰压力,提高大电网运行的安全性和稳定性.
因此,在上述研究基础上,本文研究了工业园区主动配电系统实时响应大电网系统下发电随机调峰需求的优化调度问题.首先,本文根据VRB 储能装置的充放电特性建立其数学模型,并采用三段式安全充放电控制策略求解模型;然后,本文考虑了多类型柔性负荷,并针对各类柔性负荷特性分别进行了建模处理;最后,考虑到当前电力系统调度问题一般为离散时段决策,并且各个决策时刻间具有时序相关性,将考虑电网调峰随机需求和源荷双侧随机性的工业园区主动配电系统内多类型柔性负荷与储能装置协同动态调度问题建成离散时间马尔科夫决策过程(Discrete time Markov decision process,DTMDP)模型,并采用学习优化方法对该动态调度优化问题进行策略求解.
在系统实际运行过程中,可根据观测状态及最优策略选择最优的控制行动,实时制定出各类型柔性负荷调整计划和储能装置充放电计划,从而在发、供、用电平衡协调基础上缓解电网调峰压力并实现系统安全经济运行的目标.
1 工业园区主动配电系统模型
1.1 工业园区主动配电系统
本文研究的是由工业园区调度中心、屋顶光伏、VRB 储能系统以及多类型用户负荷等组成的工业园区主动配电系统.其中,园区调度中心作为协调电网调控中心与工业用户的中间机构,可实现系统内整个负荷群的宏观整体协调响应以及微观灵活分散自治[18],进而可以调控需求侧配电系统内各类调峰资源以满足大电网实时调峰需求,同时实现系统的供需平衡以及经济运行,系统结构如图1 所示.
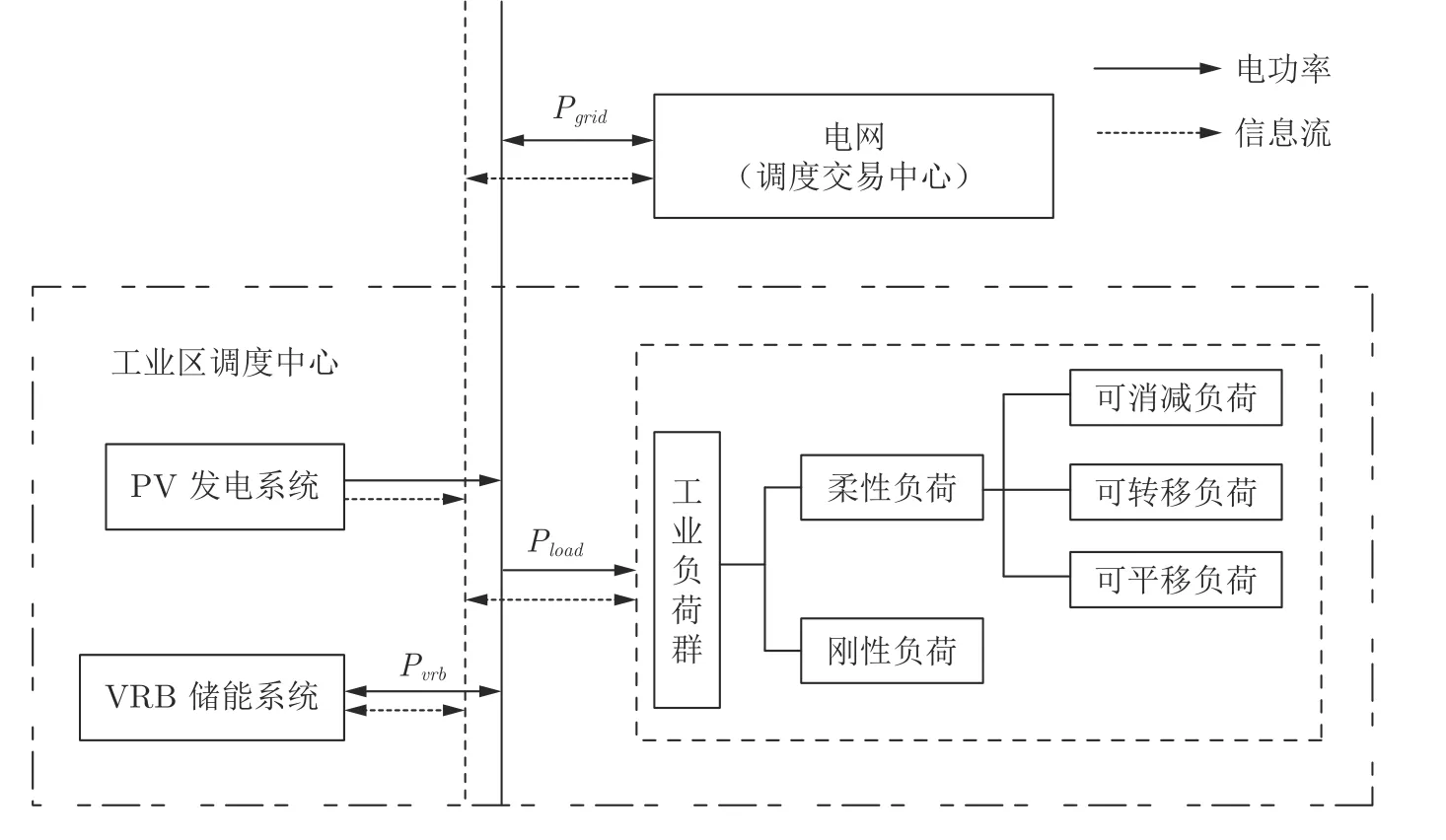
图1 工业园区主动配电系统结构模型Fig.1 Structure model of active distribution system in industrial park
主动配电系统在任意时刻t都需要满足实时供需平衡,即:


表1 部分变量符号Table 1 Partial variable symbols
本文将该系统中总负荷按需求管理模式分为刚性负荷和柔性负荷[1],其中工业园区内刚性负荷属于不可调节的用电需求,应优先被满足;园区内柔性负荷属于可控负荷,常被用于参与系统紧急调峰的需求响应[19].现将柔性负荷按响应特性分为可削减负荷、可转移负荷和可平移负荷三种类型.其中,可削减负荷指可根据需要对用电量进行部分或全部削减的负荷;可转移负荷在一个调度周期内总用电量不变,但各时段用电量可灵活调节;可平移负荷受生产流程约束,其用电曲线只能在不同时段间平移[18].各类负荷需求可表示为:
本文园区调度中心采取基于合同的直接负荷控制策略,考虑的柔性负荷只限于与园区调度中心签订合同服从其调度指令的负荷.在调度周期内,调度中心对负荷具有直接调控权,可直接控制各类柔性负荷在时序上重新调度,并在调度结束后根据负荷调整量给予一定补偿[20].
1.2 不确定性随机变量建模
由于环境和用户行为的随机特性,新能源出力与各类负荷实际需求变化既具有一定统计特征,同时也具有随机不确定性[21−22].本文涉及到的随机变量分别为PV 出力、各类负荷需求和电网调峰需求.
1.2.1 建立PV 出力模型
在系统实际运行过程中,可以根据气象数据预测得到次日的PV 出力预测曲线.设根据预测得到的t时刻PV 出力为,由于预测准确性有限,在t时刻实际PV 出力可视为预测值与随机不确定部分的叠加,表达式为:
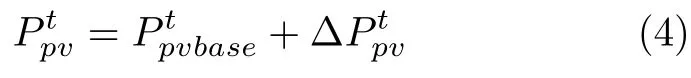
本文将PV 出力随机不确定部分的最大范围离散为−Npv ∼Npv共 2Npv+1 个等级,并将该不确定量随时间的变化过程用连续时间马尔科夫过程近似描述[23−24].即假设状态等级的逗留时间服从参数为的指数分布,在各时刻下的转移概率服从以自身状态为中心的离散高斯分布.在t时刻PV实际出力可近似描述为:
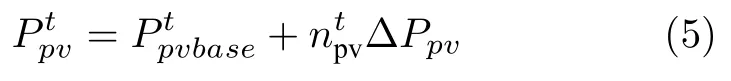
1.2.2 建立各类负荷需求模型
在系统实际运行过程中,可以通过对环境以及用户历史用电行为预测得到t时刻各类负荷需求功率.但由于各类负荷用电随机性大,影响预测的准确性,在t时刻各类负荷实际需求功率与预测值存在偏差(其中由于可平移负荷一般为固定流程生产线,故本文不考虑其随机性),则t时刻刚性负荷、可削减负荷及可转移负荷实际需求功率可分别表示为:

类似地,各类负荷需求随机不确定部分随时间的变化过程也可看作高斯—马尔科夫过程[25−27],将各类负荷随机不确定部分的最大范围区间分别离散为相应的状态等级−Nrl∼Nrl、−Ncu∼Ncu、−Nsh∼Nsh,则在t时刻相应状态等级下的各类负荷实际需求功率可分别描述如下:
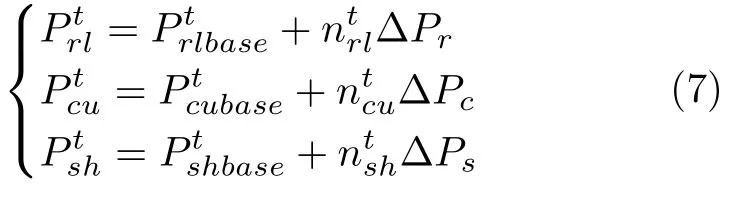
1.2.3 建立电网调峰需求模型
电网日负荷峰谷差严重影响着电力系统稳定性和发电效率,峰谷差越大,发电效率越低.调度日内,电网实时下发相应调峰指令以期减小日负荷峰谷差,从而提高电力系统运行稳定性、实现节能减排.为此,本文通过对系统内VRB 储能装置和多类型柔性负荷等需求侧调峰资源进行协调控制以满足电网调峰需求,缓解电网实时调峰压力.
由于受环境气候以及用户行为等诸多随机因素影响,电网实际下发给工业园区的调峰指令存在着相应的随机不确定部分,任意时刻t电网实际调峰需求可表示为:

类似地,将电网调峰需求随机不确定部分随时间的变化过程建模为连续马尔科夫过程,并将随机不确定部分的最大范围离散为−Npeak ∼Npeak共2Npeak+1个等级,则在t时刻相应状态等级下的电网实际调峰需求可描述为:
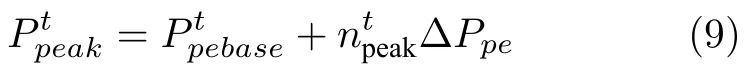
其中,∆Ppe表示t时刻电网调峰指令不确定部分离散化后的最小单位功率,状态等级···0,1,···,Npeak}.
1.3 VRB 储能模型
VRB 的电气模型有很多种,为了充分反映其充放电过程中的端电压、端电流以及SOC 等的动态变化特性,本文采用的VRB 等效电路如图2 所示[28−29].
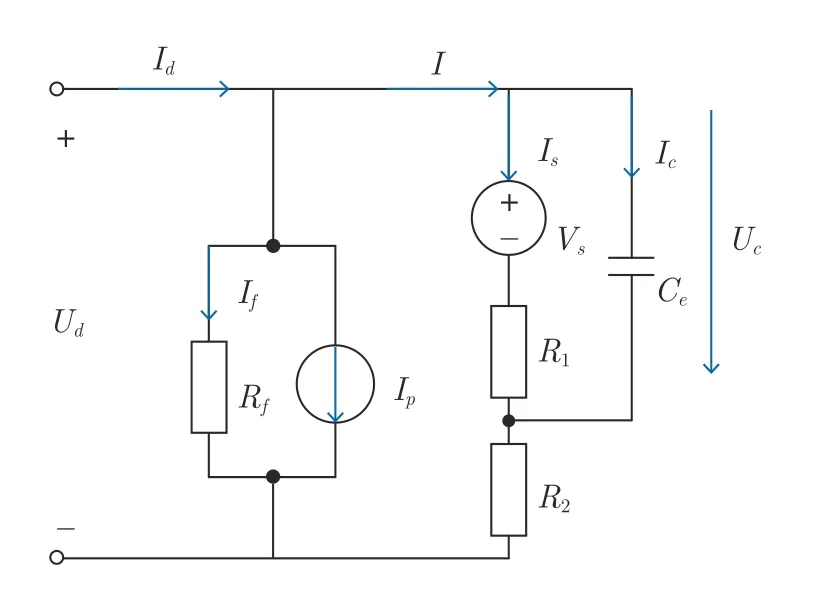
图2 VRB 等效电路图Fig.2 Equivalent circuit model of VRB
图中,Ud和Vs分别为VRB 外部端电压和内核电压,Id和Ip分别为充放电电流和泵损电流,R1和R2为等效内阻,Rf和Ce分别为寄生损耗和电极电容.
根据VRB 等效电路图,可得到其非线性数学模型如下:

在系统实际运行中,需尽量将VRB 储能装置的SOC 控制在0.2~0.8 之间以保证VRB 工作于安全区内,防止出现过充过放现象,提高电池充放电效率.本文以VRB 的端电压和SOC 作为安全充放电切换控制的约束条件,采用先恒流再恒压最后涓流充放电的三阶段式控制策略求解所建立的VRB 非线性数学模型.其中,三段式安全充放电控制策略的给定值可分别表示如下:
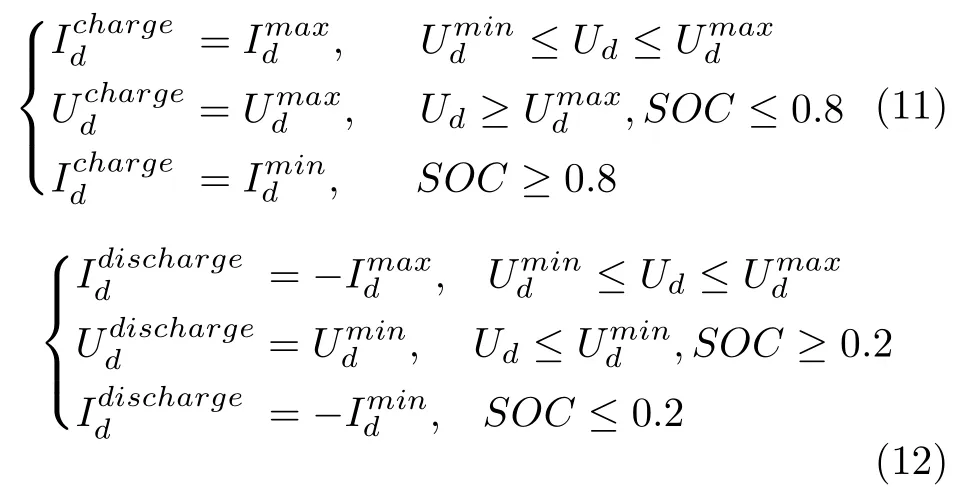
在VRB 储能装置的三段式充电过程中,端电压Ud、端电流Id及SOC 随时间的变化特性如图3所示.
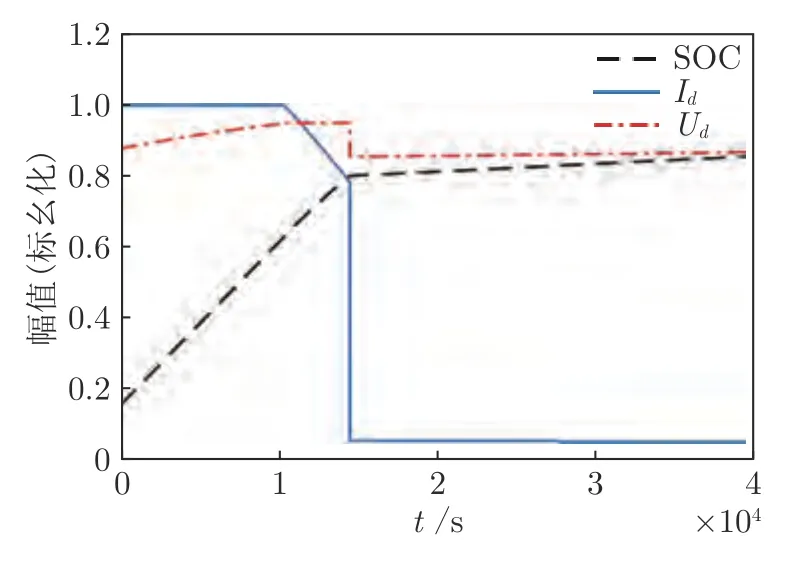
图3 采用三段式充放电策略时VRB 的充电曲线Fig.3 Charging curve using strategy three-phase of VRB
在一个周期内,VRB 储能装置约束如下[30]:
1)充放电功率约束:
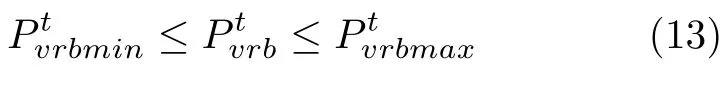
2)端电压约束:
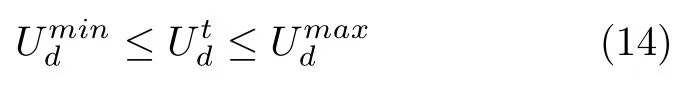
3)荷电状态(剩余容量)约束:
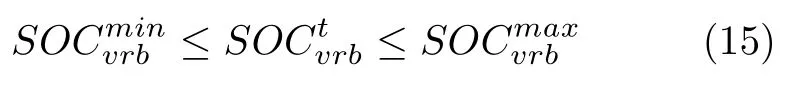
4)储能装置始末荷电状态一致约束:
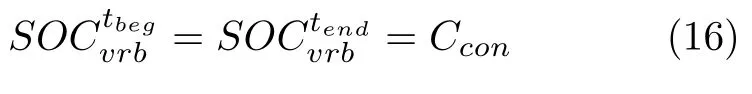
2 调度优化模型及求解
为制定各类柔性负荷调整计划和储能系统充放电计划,所求调度优化策略需考虑到任意决策时刻所有可能出现的源荷出力随机情况.为此,本文将系统决策过程建立为相应的DTMDP 模型,该调度优化模型包括状态、行动、转移代价及优化目标函数.
2.1 调度优化模型
将一天时间等分为K+1 个决策周期,采用等周期决策方式,决策时刻为tk,其中k ∈{0,1,···,K},∆tk表示决策周期k的持续时间.


系统行动包括当前状态下VRB 储能装置的充放电动作avrb∈Dvrb={−1,0,1},可削减负荷削减动作acu∈Dcu={0,1,···,Nacu},可转移负荷转移动作ash∈Dsh={−Nash,···,0,1,···,Nash}以及可平移负荷平移动作ahs∈Dhs={0,1,···,Nahs}.系统行动向量为a=(avrb,acu,ash,ahs)∈D,系统行动集为D=Dvrb×Dcu×Dsh×Dhs.
定义系统策略π为状态空间–行动集的映射,即对于任意状态sk,均可根据策略 π选择行动ask=π(sk)用以控制系统运行.
2.2 目标函数及代价
本文的优化目标是在考虑系统功率平衡、储能装置等各类约束情况下,通过学习优化的方法制定多类型柔性负荷调整计划和储能系统充放电计划,以缓解电网调峰压力并降低系统日运行代价.
假设当前时间到达决策时刻tk,通过观测可知系统处于当前状态sk,在该状态下选择行动,经过一个决策周期后,系统状态转移到下一决策周期的状态sk+1,并产生转移代价ck,由此得到一个状态转移过程为 〈sk,ask,sk+1,ck〉.其中,在决策周期k内系统运行过程中产生的各类代价可分别表示如下:

在决策周期k内通过执行行动ak状态转移过程中产生的运行代价ck可表示为:

主动配电系统调度呈一定周期性,应使每个调度周期末VRB 储能装置剩余容量等级与调度周期起始时刻一致并达到期望的容量等级,故将末状态代价设置为如下所示的差值函数cvrb(sK+1):
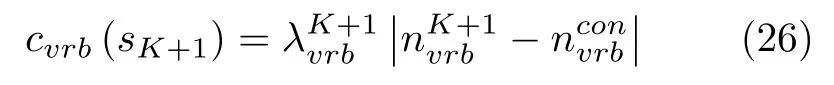
定义系统在策略π下以初始状态为s0的有限时段内优化性能准则为Vπ(s0),可表示如下:
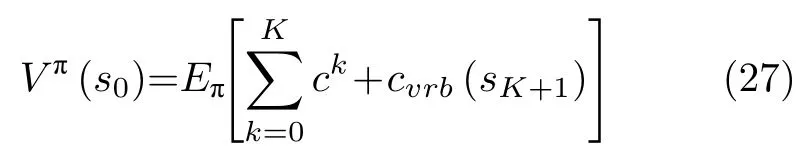
其中,ck取决于状态sk及根据策略π选取的动作ask.系统的优化目标为在策略集 Ω 中找到一个最优策略π∗,使得在该策略下系统平均日运行代价最低,即π∗=arg minπ∈ΩV π(s0).
2.3 学习优化过程
针对考虑源荷双侧随机性的工业园区主动配电系统的动态调度问题,本文采用强化学习方法对该问题进行策略求解.其中,Q 学习算法是一种模型无关的基于强化学习的随机动态规划方法,适用于求解随机环境下的最优控制策略[31].为此,本文采用基于模拟退火的有限时段Q 学习算法对所建调度优化模型进行策略求解,具体求解过程如下:
步骤1.初始化Q值表,样本轨道总数L,单条样本轨道决策周期数K+1,学习率αl,学习率更新系数ηα,模拟退火温度Ttemp及模拟退火系数ηtemp,并令当前样本轨道数l=0;
步骤2.k=0,并随机初始化系统状态sk;
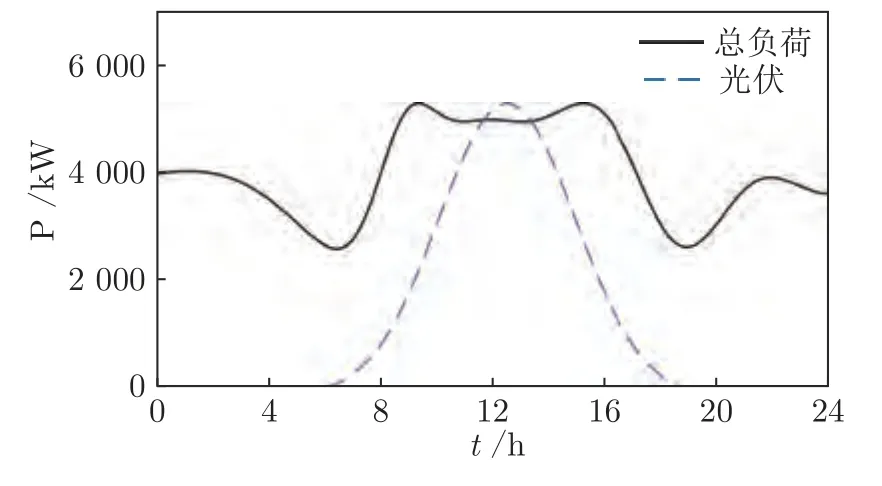
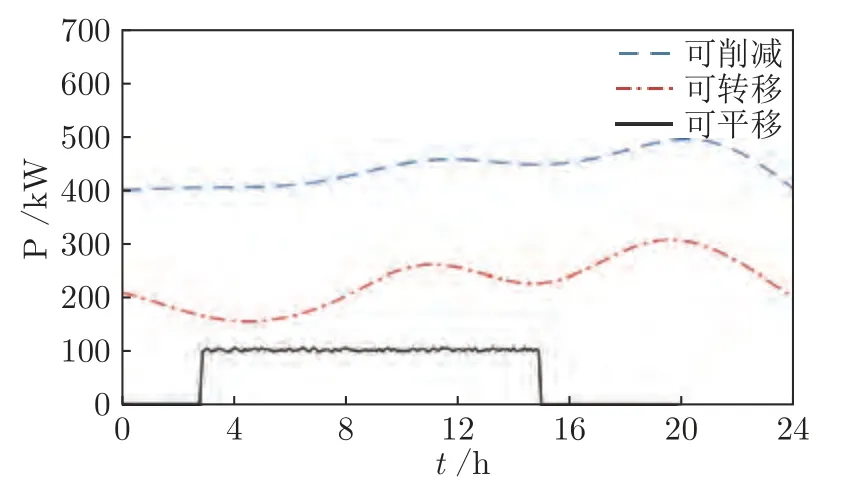
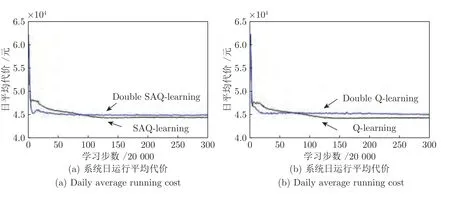
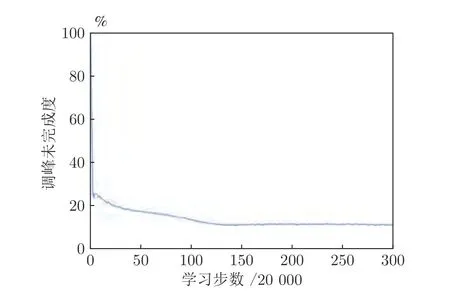
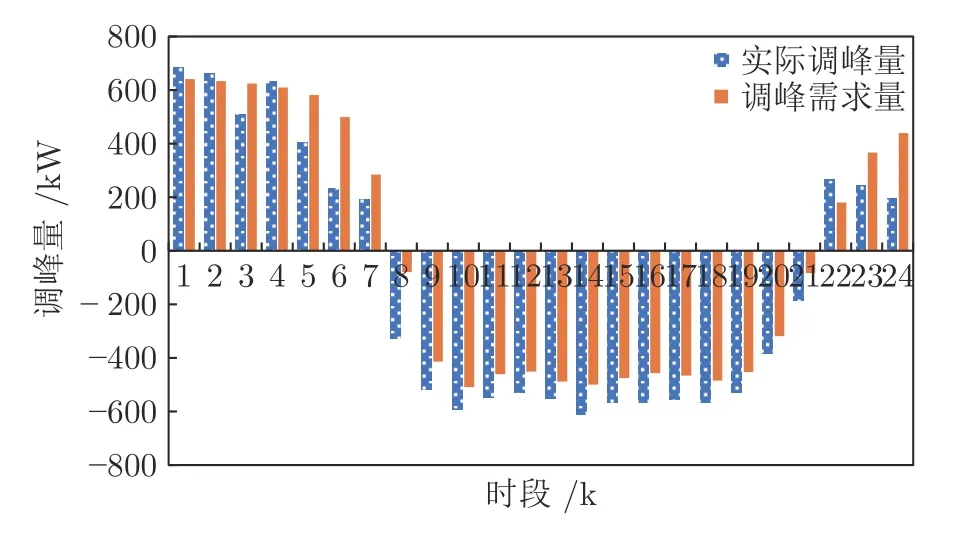
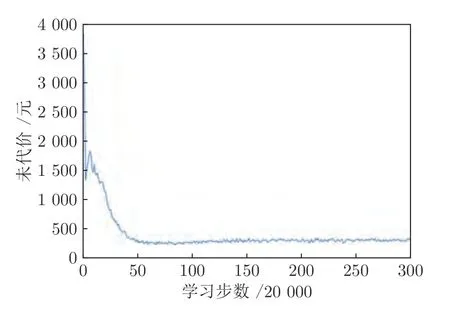
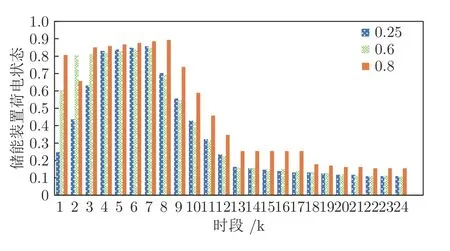
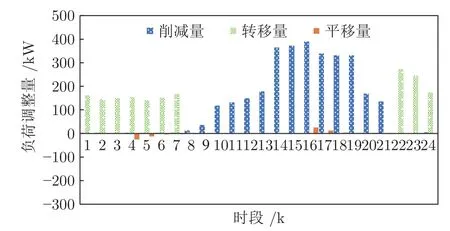
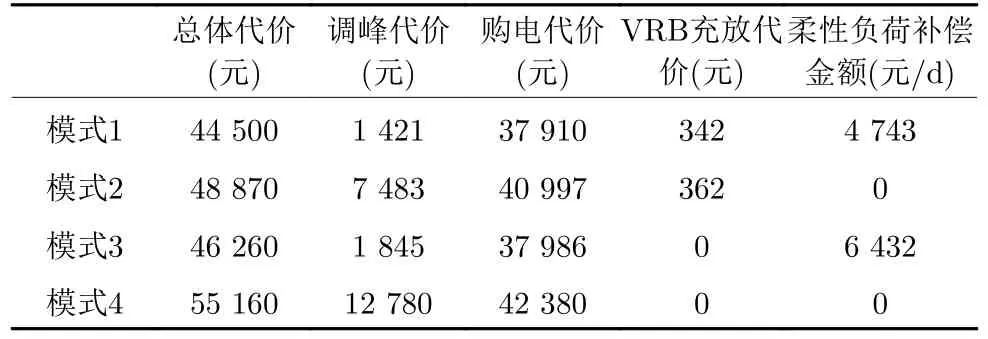
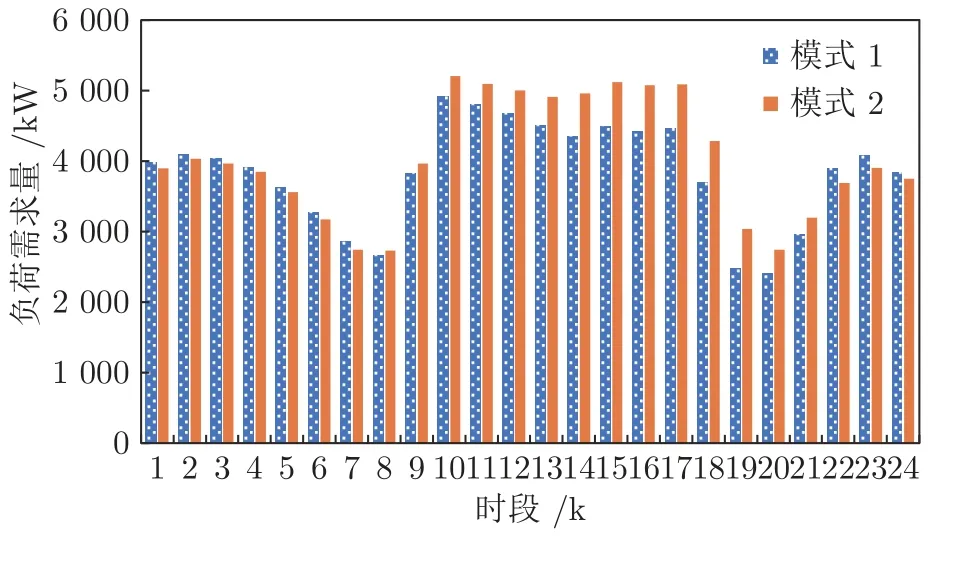
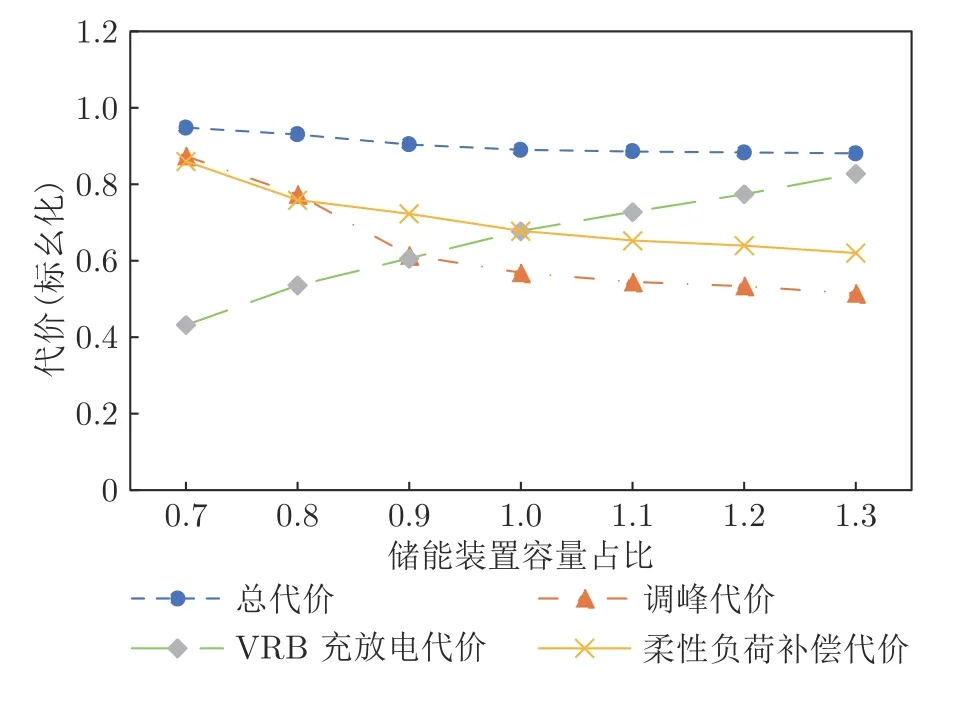
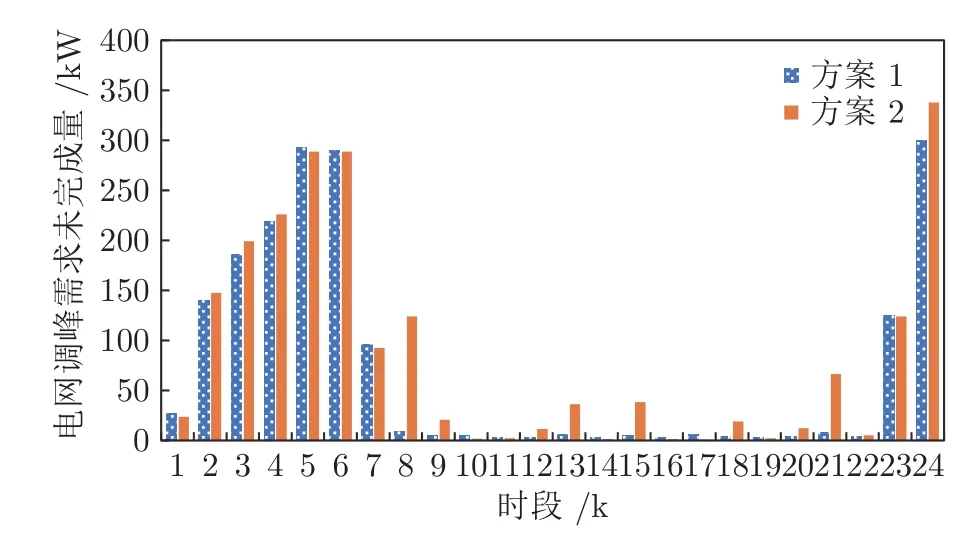
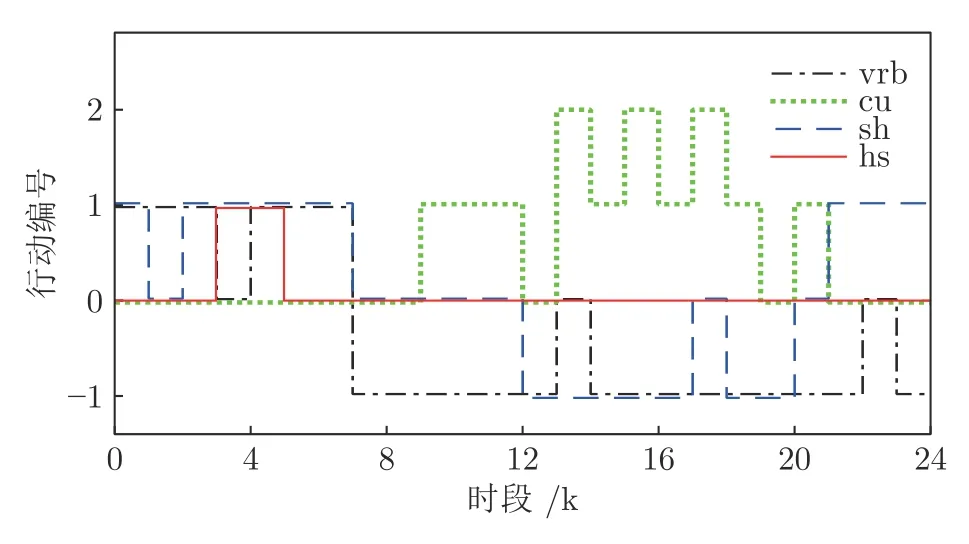
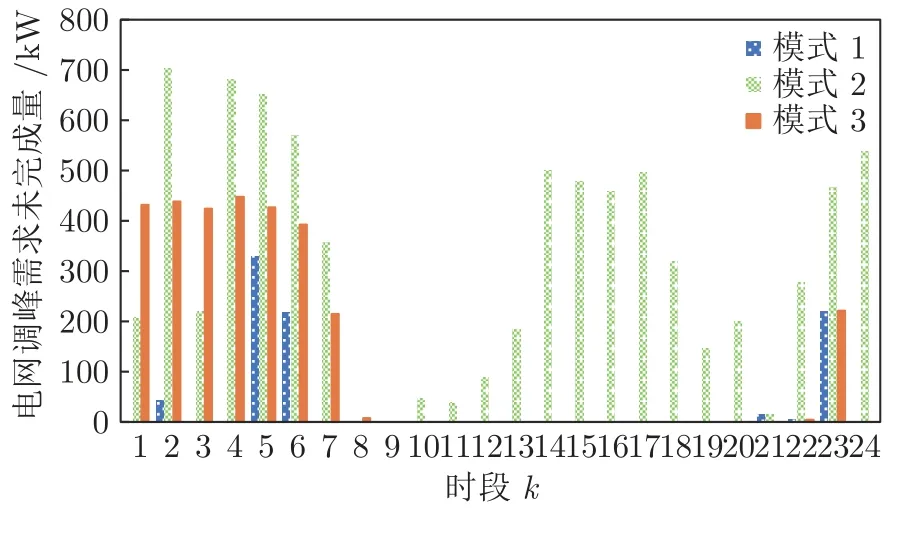
步骤3.根据Q值表和贪婪策略,选取在当前状态sk下对VRB 储能装置和各类柔性负荷的贪婪行动agreedy=arg minask∈D Q(sk,ask),同时随机选取有效行动arand.若 步骤4.执行当前所选行动ask,根据所建系统模型观察下一决策周期对应的系统状态sk+1,并计算在决策周期k内通过执行行动ask状态转移过程中产生的代价ck,根据式(28)更新Q值表,同时更新策略,即通过不断更新各状态-行动对对应的Q值和选取各状态下最小的Q值对应的储能装置充放电方案和各类柔性负荷调整方案作为该状态下新的行动,达到更新策略的目的.并令k:=k+1,返回步骤3; 步骤5.执行当前状态sK所选行动asK,并计算在决策周期K内通过执行行动asK状态转移过程中产生的代价cK及末状态代价cvrb(sK+1),并根据式(29)更新Q 值表,同时更新策略,并令l:=l+1,αl:=ηα ∗αl; 步骤6.若l 在本文算例中,根据某市各类负荷、PV 相关数据特征[21,32],拟合典型的工业园区主动配电系统内PV 出力、总负荷需求以及各类柔性负荷需求等随机因素的相应统计预测曲线如图4、图5 所示.其中,柔性负荷占园区内总体负荷需求的比例为16%,可削减、可转移、可平移3 类柔性负荷的比例分别为10 %、4.8 %、1.2 %.全天负荷整体平稳,但在早、中、晚各有一个低谷,且早晚低谷相对更低,呈现明显的日峰夜谷特点.在PV 发电装置附近配备有容量为3 MWh 的VRB 储能装置,单个VRB 储能单元相关参数如表2 所示[33].设置本文动态调度问题的决策周期为24 个时段,每个时段的持续时间为1 h. 图4 工业园区内PV 出力与总负荷需求预测曲线Fig.4 Prediction curves of PV and loads demand in industrial parks 图5 工业园区内各类柔性负荷典型日曲线Fig.5 Prediction curves of multi-type flexible loads in industrial parks 表2 VRB 模型参数设置表Table 2 Parameters of VRB 本文参照江苏省工业用户峰谷分时电价标准设定工业园区主动配电系统内各时段的具体电价,其中,高峰时段8:00—12:00 和17:00—21:00,电价为0.9947 元/kWh;低谷时段0:00—8:00,电价为0.2989 元/kWh;剩余时段的平电价为0.5968 元/kWh[34]. 根据第2.1 节可知,本文考虑到的系统状态变量和控制变量种类较多,仿真算例中所选取的状态−行动对个数更是多达7 558 272,由此形成的策略空间庞大,难以通过传统数值求解方法进行求解,因此本文采用学习优化方法对该动态调度问题进行策略求解. 1)学习优化过程分析 本文以一天24 小时为调度周期,充分利用各类柔性负荷和储能装置等可调度资源对工业园区主动配电系统进行调度协调控制,并采用基于模拟退火Q 的学习算法对该系统的动态调度优化问题进行求解.在学习过程中,通过Q 值更新公式不断更新Q 值表,得到Q 学习优化策略.设一条样本轨道为系统一日内运行过程,每经过20 000 条样本轨道,对所得策略进行一次评估,并设置策略评估过程中评估样本轨道数为3 000,对评估样本轨道结果取均值以估算系统日运行代价,图6 分别给出了传统Q 学习、双Q 学习、模拟退火Q 学习以及模拟退火双Q 学习的日平均代价学习优化曲线,各学习优化方法的收敛时间分别为54 820 s、14 803 s、44 508 s和11 154 s.从图6 中可以看出各优化算法下系统日运行代价均随着学习步数的增加而逐渐下降,并最终趋于收敛,其中,双Q 学习收敛速度较Q 学习快很多,这是因为双Q 学习是双重学习,可避免最大值带来的偏差影响,收敛更快,但Q 学习较双Q的优化效果更胜一筹;同时模拟退火Q 学习算法可利用模拟退火思想解决探索和利用的平衡问题,进而可提高收敛速度和算法性能,相较于传统Q 学习的收敛速度更快.在实际应用中,可综合考虑时间和效果进行相应优化算法的选取和实验. 图6 不同学习优化算法下的系统总学习优化过程曲线Fig.6 The optimal curve of the system under different learning optimization algorithm 图7 给出了基于模拟退火的Q 学习过程的策略性能曲线,学习曲线为每一条样本轨道所记录的日运行代价的平均值,填充区间为这3 000 条样本轨道所得数据在各点处的标准差区间,填充区域面积越小,则表明不同样本轨道得出的结果越接近,学习稳定性越好.由学习曲线可以看出系统日运行代价均随着学习步数的增加而逐渐下降,并趋于收敛,系统日运行平均代价较学习优化前降低28.7%,显著提高了系统运行效益;同时学习过程中不同样本轨道得到的数据波动并不大且随着学习步数的增加在不断减小直至趋于较小的稳定值.综上所述,本文采用的基于模拟退火法的Q 学习算法所求得的策略可以稳定、有效的适用于工业园区型主动配电系统的优化研究. 图7 系统学习优化过程的策略性能曲线Fig.7 The strategic performance curve of the system learning optimization process 图8 给出了电网调峰需求未完成度的学习曲线,经过学习优化,调峰需求未完成度逐渐降低并最终稳定在11.1% 左右;图9 为学习优化过后,各时段内电网调峰需求完成情况,明显可以看出在用电高峰时段实际调峰量完全满足其调峰需求,在用电低谷时段实际调峰量也基本完成了电网调峰需求.例如在5~7 时段,系统实际调峰量较电网调峰需求量相差较大,主要是因为从凌晨至今,大电网调峰需求均趋向于填谷,系统内储能装置SOC 已临近极值,故这段时间调峰效果稍差. 图8 调峰学习优化曲线Fig.8 The optimal curve of peak operation 图9 各时段电网调峰指令完成情况示意图Fig.9 The completion of peak adjustment instruction 图10 给出的是在随机初始SOC 情况下末状态代价的优化曲线,从图10 可以看出,通过学习优化,末状态代价可收敛在0 左右,即末状态储能剩余容量等级可达到期望值;图11 给出在不同初始荷电状态情况下,所得优化策略在一条样本轨道运行中系统内储能装置SOC 的变化情况.可以看出在不同初始荷电状态下,所得优化策略均可将荷电状态在夜间降至较低水平,且趋向于在低电价时段选取充电或闲置,而在用电高峰时段趋向于放电或闲置,以获取因电价差值产生的收益,缓解大电网的调峰压力,进而提高工业园区主动配电系统运行的经济性并提升需求侧调峰效果. 图10 末代价学习优化曲线Fig.10 The optimal curve of final cost 图11 不同初始荷电状态下各时段SOC 变化情况Fig.11 Changing process of SOC under different initial values 图12 为学习优化前后需求侧负荷曲线,由图12可以看出,与原负荷曲线相比,学习优化策略对工业园区主动配电系统有一定的调峰效果,学习优化前后系统总负荷特征如表3 所示.由表3 可知,学习优化前系统负荷峰谷差为2 689 kW,通过学习优化对系统内多类型柔性负荷选取控制行动,使峰谷差减少为2 535 kW,系统峰谷差降低5.7 %.上述结果说明通过学习优化不但可以满足电网调峰需求,而且可以在一定程度上降低系统自身峰谷差,有利于主动配电系统安全经济运行. 图12 学习优化前后系统负荷曲线Fig.12 The curves of load before and after learning optimization in the system 表3 学习优化前后系统总负荷特征Table 3 The characteristic of load before and after learning optimization in the system 图13 为学习优化后系统内3 类典型柔性负荷在调度日内各时段下的实际调整量,可以看出可削减负荷的削减量在负荷用电高峰期明显高于用电低谷期,可转移负荷趋向于将自身负荷用电从用电高峰转移到用电低谷,可平移负荷由于自身特性和限制只会小范围向后平移.通过对各类柔性负荷的动态调整可在一定程度上减缓电网调峰压力,并在一定程度上实现峰电谷用. 图13 学习优化后各时段典型柔性负荷调整量Fig.13 Adjustment of multi-type flexible loads after optimization 2)不同调度模式下的优化结果对比分析 在相同配置情况下,将VRB 储能装置与柔性负荷协同优化调度模式记为模式1;将仅考虑VRB储能装置的优化调度模式记为模式2;将仅考虑柔性负荷的优化调度模式记为模式3;将既不考虑VRB 储能装置也不考虑柔性负荷的优化调度模式记为模式4.4 种模式对应于系统不同的物理结构,其策略维度也不同,故分别对应不同的策略,分别记为策略1,2,3,4.现分别将其他模式对应的优化效果与模式1 进行比较,在各优化调度模式下主动配电系统运行过程中产生的日运行代价和调峰完成情况对比如图14 所示,各项代价指标的具体数值如表4 所示. 图14 不同调度模式下的调峰效果比较图Fig.14 Comparison effect of peak operation under different dispatching modes 表4 不同调度模式下的相关指标Table 4 Related indexes under different dispatching modes 由表4 数据可以看出各模式下系统优化效果由好到差分别为:模式1、模式3、模式2、模式4.由图14 可以看出,模式1 下的电网调峰需求完成度明显优于其他3 种模式,且模式1 下的系统日平均运行代价最低:模式2 的调峰完成度较差,主要是因为在模式2 下电网调峰需求由VRB 储能装置充放电来完成,然而各时刻下充放电功率与储能装置实际容量有关,无法动态调节,在一定程度上受到很大限制,而模式1 和模式3 中电网调峰需求可通过调节各类典型柔性负荷来完成,可动态调节,更有利于大电网调峰任务的完成.上述结论充分说明了本文引入VRB 储能装置与多类型柔性负荷进行协同优化调度的有效性. 由图15 可以看出,模式1 与模式2 的策略相比,负荷需求有明显差异,在负荷用电高峰时段模式1 的负荷需求明显低于模式2,而在负荷用电低谷时段模式1 的负荷用电需求又高于模式2,说明了策略1 通过在不同时段对各类型柔性负荷选取不同行动,即用电高峰选取削负荷行动,并将部分可转移、可平移负荷由高峰用电移至低谷,在一定程度上实现了削峰填谷,发挥了柔性负荷的调峰作用. 图15 不同调度模式下负荷优化结果比较图Fig.15 Comparison diagram of load optimal results under different dispatching modes 以模式1 选取的VRB 储能装置容量配置为基准,分别求解不同储能装置容量配置下对应的优化调度方案,经优化得到不同容量占比下系统运行过程中的各项代价比较情况如图16 所示.由图16 可知,随着储能装置容量的增加,系统日运行总代价缓慢降低,并且未完成电网调峰需求产生的调峰代价以及柔性负荷的补偿代价逐渐减小,储能装置充放电过程产生的损耗也逐渐增加,说明了在允许范围内适当增加储能装置的容量配置可以提高电网调峰需求完成度和降低系统日运行代价. 图16 不同储能容量占比下的各项代价比较图Fig.16 Comparison of costs under different proportion of energy storage capacity 以模式1 设置的各类柔性负荷占比为基准,分别求解不同柔性负荷占比下的优化调度方案,所得系统运行过程中产生的各项代价指标的变化趋势如图17 所示.由图17 可明显看出,随着柔性负荷的占比增加,系统运行过程中因调节各类柔性负荷需补偿的代价逐渐增加,而因未完成电网调峰需求产生的调峰代价先是逐渐降低直至柔性负荷占比为所设基准值的90%左右,此时若继续增加柔性负荷占比调峰代价则呈上升趋势,并且系统总体运行代价趋势与调峰代价趋势基本一致. 图17 不同柔性负荷占比下的各项代价比较图Fig.17 Comparison of costs under different proportion of flexible load 根据光伏及负荷统计预测曲线,在模式1 结构下,将源荷双侧随机因素作为系统状态和不作为系统状态的两种优化求解方式分别记为方案1 和方案2.将方案2 与方案1 所得的优化策略在随机环境下进行评估比较,结果如表5 和图18 所示. 从图18 可以看出总体上各时段内方案1 的优化策略对应的电网调峰需求未完成量要小于方案2,且方案1 在用电高峰时段下的调峰未完成量均趋于0,故方案1 的调峰效果明显好于方案2.由表5可知方案1 下的系统日运行代价相比于方案2 更低,且其调峰完成度也高于方案2.以上现象均说明了本文采用的将源荷双侧随机因素作状态的方案1与不将随机因素作状态的方案2 相比,其所得优化策略能够更加经济地适用于实际的随机环境,并可进一步提高电网调峰需求完成度. 表5 不同方案下的相关指标Table 5 Related indexes under different projects 图18 不同方案下的调峰需求未完成量比较图Fig.18 Unfinished amount of peak operation demand under different projects 3)学习优化策略分析 在所得优化策略下对一条样本轨道进行学习,可以观测得到该条仿真样本轨道中各时段PV 发电功率、各类负荷需求、电网调峰需求和电池荷电状态等实际状态值,以及相应状态下采取的最优控制行动如图19 所示,表6 记录了调度日内该样本典型状态和行动. 图19 优化策略下各时段行动选取情况Fig.19 Choice of action pairs under optimal policy 由图19 和表6 可知,VRB 储能装置在低电价时更趋向于选取充电动作来储存电量以备即将到来的负荷用电高峰,在高电价时则倾向于选取放电动作,利用存储的电能为负荷供电,以降低在用电高峰购电代价以及负荷高峰期的用电需求,获取“低价储电,高价卖电”的经济收益,这种低储高放方式不但可以赚取电价差的利润而且可以缓解电网调峰压力;可削减负荷在用电高峰期倾向于大幅度的削减负荷用电,在用电低谷期则不削减负荷用电;可转移负荷倾向于将负荷从高峰用电转移到低谷用电;可平移负荷向后平移2 个时段,使时间跨度由3:00—15:00 变为5:00—17:00,避免了夜间工作为工人带来的不便利.例如,在4 时低负荷、低电价的情况选择储能装置的动作为充电,可削减负荷的动作为不削减,可转移负荷的动作为转入,可平移负荷的动作是向后平移. 表6 优化策略下部分状态行动Table 6 Partial state-action pairs under optimal policy 针对模式1,2,3 所得相应的调度优化策略1,2,3,可得到各策略在同一样本轨道下各时段的调峰完成情况如图20 所示,可以看出模式1 下该样本的调峰未完成量明显小于模式2、3,且其在负荷高峰期的调峰未完成量均为0,完全满足电网在用电高峰期的调峰需求.表7 给出了各优化策略在该样本轨道下产生的各项代价指标,根据表中数据分析可知模式1 下的日运行费用也明显小于其他模式,说明了在单条样本下,考虑多类型柔性负荷与储能装置协同调度所得策略的优化效果更好,进一步证明了本文优化方法的有效性. 表7 优化策略下不同模式的相关指标Table 7 Related indexes under different modes in optimal policy 图20 优化策略下不同模式的调峰需求未完成量比较图Fig.20 Unfinished amount of peak operation demand under different modes in optimal policy 本文研究的是考虑电网调峰需求的工业园区主动配电系统内动态经济调度优化问题,并在此基础上考虑了源荷双侧不确定因素,将工业园区主动配电系统调度问题建立为马尔科夫决策过程模型,采用模拟退火Q 学习算法对该动态问题进行策略求解.仿真结果表明,考虑多类型柔性负荷和储能系统协同调度相比于传统单一模式可显著降低电网调峰需求未完成度以及提高系统运行效益,并且学习优化所得控制策略能够在考虑源荷随机情况下降低系统的运行成本,降低自身峰谷差,可在很大程度上满足电网调峰需求,有利于主动配电系统经济运行和提高电力系统运行稳定性. 由于本文考虑的系统状态和行动种类多,若后续考虑将系统状态和行动连续化以获取更加精确的模型和更高精度的控制效果,可能会导致维数灾问题,探索解决该类问题的方法十分值得进一步研究;同时,由于系统故障或人为行为等因素带来的系统物理结构的动态变化,考虑系统结构动态切换场景下的策略优化问题也是值得深入研究的一个方向;此外,随着新能源渗透率和柔性负荷规模的日益增大,考虑在源荷互动、多方参与的复杂电力市场交易环境下系统内各部分利益间的博弈问题以及多类型市场机制对系统调度优化的影响也是有意义的研究方向.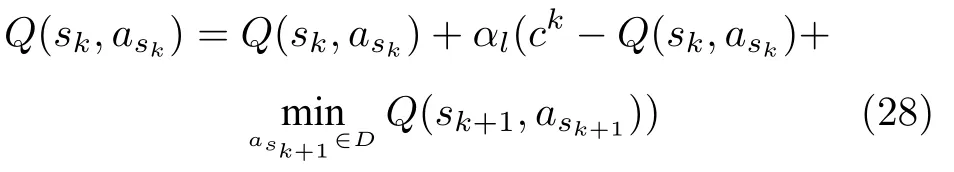
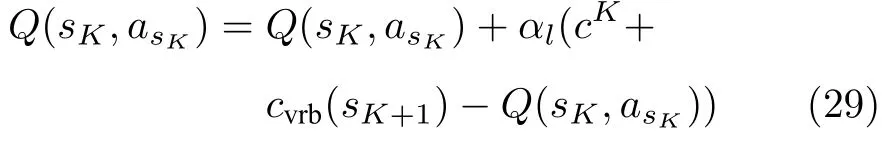
3 算例分析
3.1 算例描述

3.2 仿真结果分析








4 结论
