耦合气溶胶双参数化方案的大气能见度数值改进算法

张智察,倪长健,赵军平,冯 淼,谢滟馨,王杨菲

耦合气溶胶双参数化方案的大气能见度数值改进算法

张智察1,2,倪长健1*,赵军平2,冯 淼3,谢滟馨1,王杨菲1

(1.成都信息工程大学大气科学学院,高原大气与环境四川省重点实验室,四川 成都 610225；2.浙江省气象台,浙江 杭州 310017；3.成都市环境保护科学研究院,四川 成都 610072)

将气溶胶复折射率(Aerosol Complex Refractive Index, ACRI)和气溶胶粒径吸湿增长因子(Growth Factor,(RH))参数化方案进行耦合,提出了一种基于Mie散射模型的大气能见度数值改进算法.并利用成都市2017年10～12月WS600一体式气象站、AURORA-3000积分浊度计、AE-31黑碳仪以及GRIMM180环境颗粒物监测仪分别观测获得的相对湿度(RH),干气溶胶散射系数(sp),干气溶胶吸收系数(sp),气溶胶质量浓度(PM10, PM2.5, PM1)及其数浓度粒径分布([(RH)])的地面逐时观测资料,通过与两种能见度计算模型(经验参数的Mie散射模型和统计模型)在不同能见度区间(<2km, 2～5km, 5～10km, >10km)模拟结果的对比分析,评估了该改进算法的适用性.结果表明:三种能见度计算方法均能较好地模拟出能见度的变化特征;改进算法通过本地化参数化方案更准确地估计出DACRI和(RH),从而可更准确地模拟出四类能见度区间,对应模拟值与实测值的相关系数()分别为0.62, 0.90, 0.89, 0.93,平均相对误差(MRE)分别为9.86%, 10.39%, 9.94%, 14.06%.

气溶胶；复折射率；吸湿增长因子；参数化方案；能见度

随着我国社会经济的迅猛发展以及城市化进程城的不断加快,以大气能见度降低为主要特征的霾在秋冬季频繁发生[1].能见度降低不仅表征环境空气质量的恶化,也对人体健康和交通运输安全产生严重影响[2].

Koschmieder于1924年就提出了关于大气能见度与消光系数的关系,即大气能见度与消光系数之比为常数[3].因此,明晰大气消光系数的演化机理就成为对能见度研究的关键技术环节.诸多研究表明,气溶胶消光系数是大气消光系数的主体,其占比通常都在90%以上[4-5].目前,针对气溶胶消光系数或能见度的参数化方案主要包括统计模型和利用Mie散射的计算模型两种.

统计模型的核心是建立大气消光系数或能见度与其影响因子之间的统计关系[6].早在1985年,美国Improve计划就率先建立了PM2.5中各化学组分质量浓度与气溶胶消光系数之间的定量关系,这为早期的能见度预报提供了有效的计算方案[7].进一步研究指出[6,8-9],由于PM2.5中某些化学组分的散射消光能力存在显著的时空差异性,利用Improve关系式计算的散射系数可能大大偏离实际的观测数据.影响能见度的因素非常复杂,针对多区域的研究一致表明,颗粒物浓度尤其是细颗粒物质量浓度在区域能见度下降中占据主要地位[9-10].另外,Liu等[11]系统性研究了京津冀地区气溶胶消光系数随相对湿度的变化特征,发现当相对湿度小于85%时,气溶胶散射吸湿增长因子(RH)平缓增长,而当相对湿度大于85%时,(RH)急剧增大,表明气溶胶的吸湿增长特性是导致高湿条件下能见度急剧下降的重要诱因.白永清等[12]分析了武汉地区能见度与PM2.5质量浓度和相对湿度之间的非线性关系,指出细颗粒物浓度和相对湿度共同制约了能见度的变化.Chen等[13]利用HaChi外场观测数据的研究发现,相比于仅利用气溶胶体积浓度和相对湿度构建的消光系数参数化方案,考虑以气溶胶数浓度的消光系数参数化方案可以显著提升低能见度的模拟效果.

近年来,随着环境监测技术的发展,基于Mie散射模型的气溶胶消光或能见度模型也得到了深入的研究和应用.Chen等[14]利用在杨村观测的粒度谱、不同模态的气溶胶吸湿增长因子和环境消光系数,基于Mie散射计算气溶胶消光系数,得到的计算值与观测值吻合较好.虽然基于Mie散射模型的气溶胶消光系数计算模型物理意义清晰,但模型关键参数的取值存在较大经验性和人为任意性[11,13-14].气溶胶光学参数的实际变化是非常复杂的,其经验取值是大气消光系数计算不确定性的重要来源[5].为此,张智察等[15-16]利用免疫进化算法先后提出干燥条件下气溶胶复折射率(DACRI)和气溶胶粒径吸湿增长因子(RH)的反演方法,并基于成都地区DACRI与主要颗粒物质量浓度指标的统计分析,进一步构建了适用于该区域的DACRI和(RH)的参数化方案.

因此,着眼于改善目前统计模型与Mie散射模型中大气能见度模拟所需的关键参数取值的不确定性[17-18],以提升大气能见度的模拟精度,将DACRI和(RH)参数化方案进行耦合,提出了基于Mie散射模型的能见度改进算法,并在成都地区进行了实例验证,以期为区域能见度预报能力和大气环境管理水平的提升提供技术支持.

1 材料与方法

1.1 观测仪器

使用的数据包括成都市2017年10～12月由WS600一体式气象站、AURORA-3000积分浊度计、AE-31黑碳仪以及GRIMM180环境颗粒物监测仪获取的逐时观资料.

相关仪器介绍如下:(1)AURORA-3000型浊度计(Ecotech公司,澳大利亚)观测波长为525nm,采样频率为5min/次,TSP切割头,检测范围>0.25Mm-1,每24h进行零点检查, 24h零点漂移<±1%,每周用R134a气体进行跨度标定,通过内部温湿度传感器来控制浊度计内部加热系统,使得仪器内部腔室中气溶胶相对湿度控制在40%以下,将其作为气溶胶的干燥状态.(2)AE-31型黑碳检测仪(Magee Scientific公司,美国)观测黑碳(BC)质量浓度,数据采集频率为5min/次.黑碳仪采用TSP切割头,采样头与仪器连接中间增设硅胶管减少水分对黑碳测量的影响.浊度计和黑碳仪的监测资料经过质量控制后统一处理为小时均值数据.(3)GRIMM180环境颗粒物监测仪(GRIMM公司,德国)可以实时测量大气中PM10, PM2.5和PM1的颗粒物质量浓度以及31个粒径段的气溶胶数浓度,据此获得气溶胶粒子谱分布n[(dry)],其数据频率为5min/次,其中各粒径段粒子直径的起始值分别为0.25, 0.28, 0.3, 0.35, 0.4, 0.45, 0.5, 0.58, 0.65, 0.7, 0.8, 1.0, 1.3, 1.6, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 6.5, 7.5, 8.0, 10.0, 12.5, 15.0, 17.5, 20.0, 25.0, 30.0, 32.0mm.(4)气象要素(大气能见度和相对湿度RH)由WS600(LUFFT公司,德国)一体式气象站进行监测;气态污染物NO2体积浓度由化学发光NO, NO2-NO分析仪(Thermo 42i,美国)进行监测.

1.2 观测地点

GRIMM180大气颗粒物监测仪观测点位于成都市一环路联益大厦(104°02¢E,30°39¢N)顶楼,距地面81m.其余仪器观测点位于成都市环境保护科学研究院综合大楼楼顶(30°39¢N,104°02¢E),距离地面21m,四周2km内无高大建筑物,视野开阔,周围是集中居住区.两处监测点位周围无明显大气污染源,二者直线距离为410m,环境气象条件基本一致.

1.3 资料处理方法

将上述监测数据统一处理成小时均值数据.剔除了出现降水、沙尘以及大风现象所在日的全部数据;其次,剔除仪器烘干后相对湿度仍大于40%的异常数据,以排除水汽影响;最后,剔除超出界限值数据,连续无变化数据,缺测数据以及气溶胶质量浓度存在倒挂等异常数据,由此获得匹配样本1145个.

大气消光系数代表光线在大气中传播单位距离时的相对衰减率,在550nm波长处的环境大气消光系数ext(RH) (km-1)与大气能见度(km)的关系见式(1)和式(2)[19].

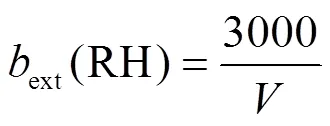
ext(RH)=sp(RH)+ap+sg+ag(2)

式中:sp(RH),ap,sg,ag,sp分别是550nm波长处环境条件下气溶胶散射系数,气溶胶吸收系数,干洁大气散射系数,干洁大气吸收系数,单位为Mm-1.

依据文献[20-21],按式(3)将AURORA-3000积分浊度计观测的525nm波长处的干气溶胶散射系数sp, 525nm订正得到550nm波长处的干气溶胶散射系数(sp),式中= 1.36,代表了成都市Angstrom波长指数[22].

根据吴兑等[2]针对AE-31型黑碳检测仪的对比观测试验原理,利用AE - 31型黑碳检测仪直接观测得到未经订正的880nm波长处黑碳(BC)质量浓度(BC)/μg·m-3,按式(4)反演532nm波长处的气溶胶吸收系数ap, 532nm(Mm-1),并由式(5)订正得到550nm波长处的吸收系数ap(Mm-1),见式(4).

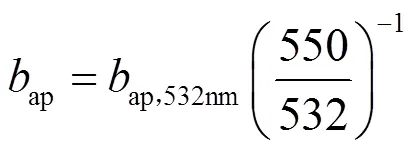
参照Penndorf(1957)[23]的研究成果,对应550nm波长处的sg一般取值为13Mm-1.参照Sloane (1985)[24]的计算方法,对应550nm波长处的ag的计算见式(6).

式中,NO2为NO2质量浓度(10-9g/m3).

2 能见度计算方案的设计

作为大气消光系数的主体,气溶胶散射系数极易受颗粒物质量浓度、颗粒物化学组分以及气溶胶吸湿性的影响,一直以来是大气消光系数和能见度预报不确定性的重要来源.因此,气溶胶散射系数的计算方法是决定能见度计算精度的关键.

本文将前2/3时间序列的样本(763)作为下文三种大气能见度计算方案的建模数据集.后1/3时间序列的样本(382)作为验证数据集,用于比较各个方案在大气能见度模拟中的适用性.首先将大气能见度划分为<2km, 2～5km, 5～10km以及>10km这4种范围,并对应给出了这4种范围大气能见度条件下常规气象要素的统计结果(表1).从表1可见,大气能见度越低,对应的PM2.5, BC, RH总体越高.

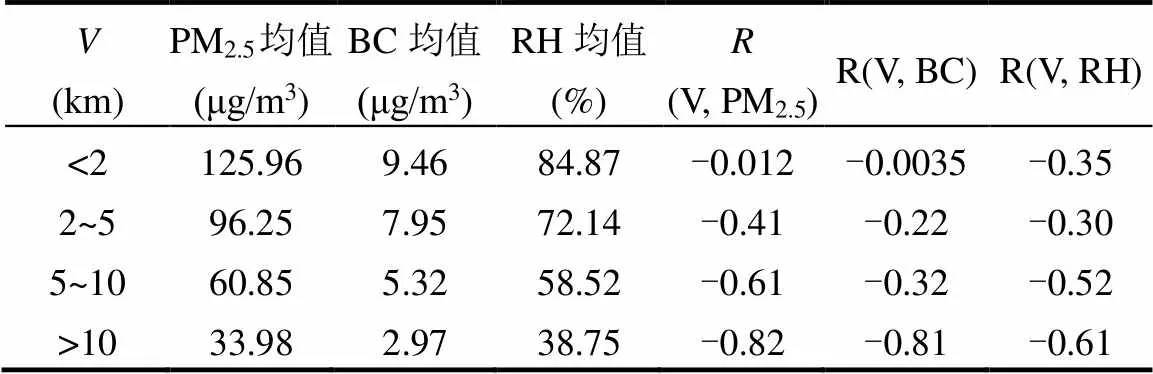
表1 4种范围大气能见度下常规气象要素的统计结果

注:(, PM2.5),(, BC),(, RH)分别表示与PM2.5质量浓度, BC, RH之间的相关系数.

2.1 能见度计算的统计模型(方案一)

气溶胶散射吸湿增长因子(RH)是环境条件下气溶胶散射系数与对应干燥条件下气溶胶散射系数的比值.根据已有的研究成果[25],成都地区秋冬季(RH)的计算公式见式(7).

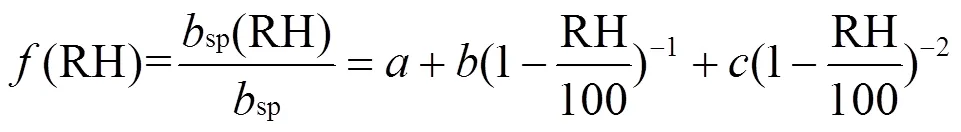
根据式(2),式(7)以及sp和PM2.5之间的统计关系[26],ext(RH)的计算公式见式(8).

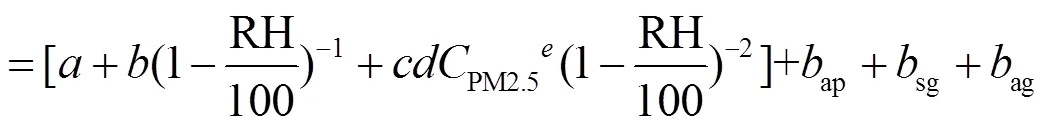
根据式(8),利用前述建模数据求解各待定参数,得到成都地区秋冬季ext(RH)的统计模型,见式(9).

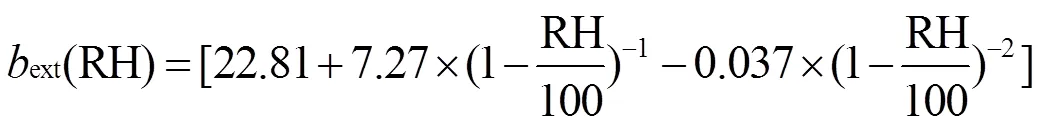
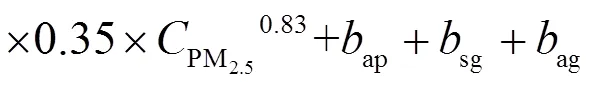
至此,利用式(9)计算ext(RH),再根据式(1)计算获得了大气能见度,建模计算结果表明,大气能见度的计算值总体较观测值略低3.81%,两者之间的和MRE分别为0.94和18.01%.其中,4种大气能见度模拟值与其观测值之间的分别为0.66、0.75、0.59和0.83, MRE则分别为12.42%、18.56%、17.21%和19.64%.

2.2 能见度计算的经验参数Mie散射模型(方案二)

基于Mie散射理论[15-16,27-28],ext(RH)的计算公式见式(10).

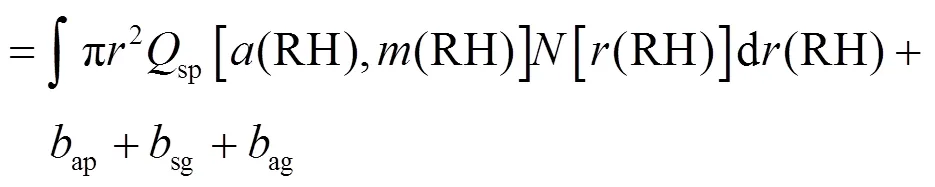
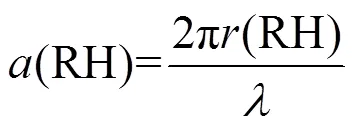
(RH) =re(RH) +i(RH) (12)

式中:(RH)是环境条件下气溶胶的尺度参数;re(RH)和i(RH)是环境条件下气溶胶复折射率(DACRI)(RH)的实部和虚部;sp[(RH),(RH)]是由Mie散射模型计算出的环境条件下气溶胶散射效率因子,由(RH)和(RH)决定;(RH)是环境条件下的气溶胶粒径;[(RH)]是环境条件下气溶胶数浓度粒径分布;(RH)是环境条件下气溶胶的粒径.环境条件下气溶胶尺度参数(RH)和复折射率(RH)可进一步分解为式(13-17)[29-30].

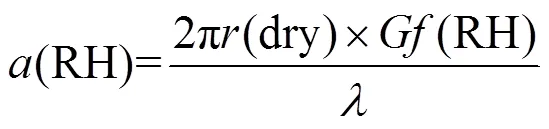
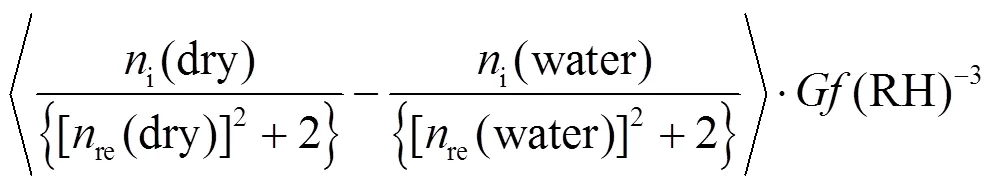
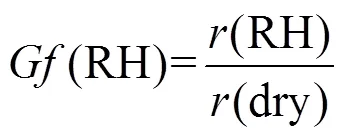
(dry) =re(dry) +i(dry) (16)

(water) =re(water) +i(water)=1.33+0×i (17)

式中:(RH)为气溶胶粒径吸湿增长因子;(dry)为干燥条件下气溶胶的粒径;re(dry)和i(dry)为干燥条件下气溶胶复折射率(dry)的实部和虚部;re(water)和i(water)为水复折射率(water)的实部和虚部.

由于DACRI观测与反演的复杂性,其实部re(dry)和虚部i(dry)在以往研究中通常分别被经验假定为1.55与-0.005[13].另外,基于孙景群等提出的(RH)参数化方案,见式(18).

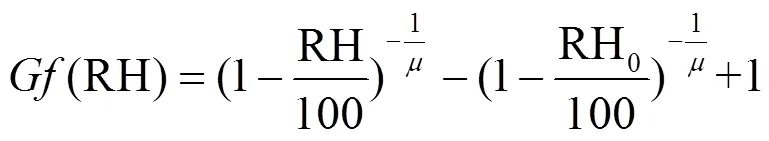
DACRI和(RH)是基于Mie散射模型模拟大气能见度所必须的关键光学参数,但受制于DACRI和(RH)观测与反演的复杂性,以往研究中re(dry)、i(dry)与(RH)参数化方案的参数()通常为经验取值.为此,本文首先采用式(18)的参数化方案来计算(RH),由于成都地区的气溶胶类型为污染型,再参考孙景群与Kasten等的研究成果[29-31],本文将式(18)中的参数假定为4.4.

在上述re(dry)、i(dry)与(RH)经验取值的情况下,基于建模数据集,根据式(1)可求得大气能见度,建模计算结果表明,re(dry)和i(dry)的经验取值与观测值之间不存在相关性(由于DACRI的经验定值),对应的MRE则分别为3.37%和77.80%,根据式(18)(=4.4的经验取值)所计算的(RH)与观测值之间的和MRE则分别为0.92和18.19%,根据式(18)计算的re(RH)和i(RH)与其观测值之间的分别为0.58和0.47,对应的MRE则分别为6.23%和82.15%,大气能见度的计算值较观测值平均低23.80%,其对应的和MRE分别为0.96和24.53%.其中,4种大气能见度模拟值与其观测值之间的分别为0.71,0.81,0.68和0.91, MRE则分别为29.63%,26.01%,26.81%和18.69%.从方案二的建模计算结果可见,re(dry)经验取值与其观测值之间的误差较小,但i(dry),(RH)以及大气能见度与其观测值之间的误差均很大.

2.3 能见度计算的双参数化方案Mie散射模型(方案三)

针对方案二中DACRI与(RH)经验取值的不确定性,张智察(2020)在分析DACRI与颗粒物质量浓度统计关系的基础上,利用多元逐步线性回归方法,提出了DACRI的参数化方案,见式(19)和式(20).

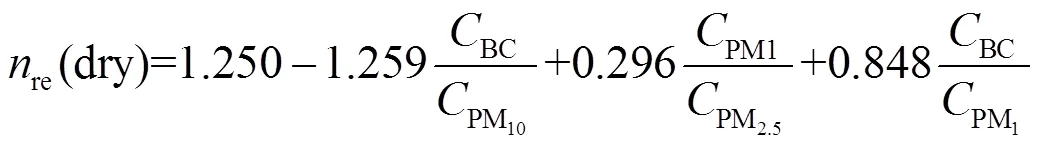
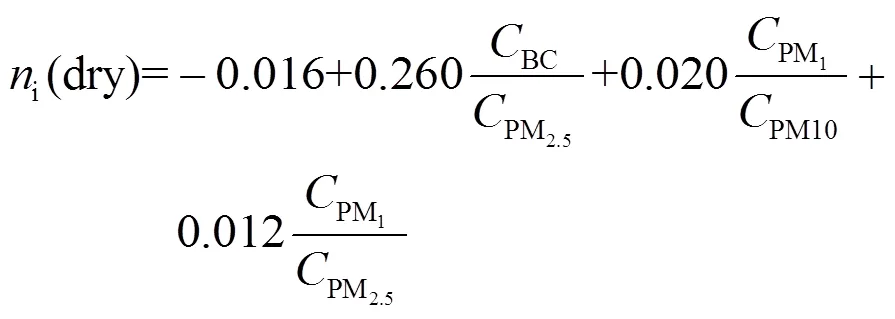
式中:BC,PM1,PM2.5和PM10分别为BC, PM1, PM2.5和PM10的质量浓度,单位为μg/m3.

不同类型气溶胶粒径吸湿性差异很大,即便是同一类型的气溶胶,受排放源以及气溶胶物化过程的影响,气溶胶粒径吸湿性也有差异.为此,张智察等[16]通过结合免疫进化算法与Mie散射理论反演(RH),分析了其与RH之间的关系,并基于式(18)提出了适用于成都地区秋冬季的(RH)参数化方案,见式(21).

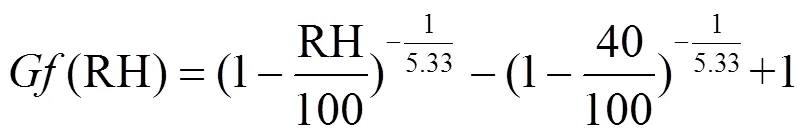
基于建模数据集,首先分别根据式(19)和式(20)分别计算re(dry)和i(dry),式(21)计算(RH).在此基础上,大气能见度的计算流程与方案二相同.最终计算结果表明,根据式(19)和式(20)计算的re(dry)和i(dry)与观测值之间的分别为0.55和0.85,对应的MRE分别为2.27%和14.72%,根据式(21)计算的(RH)与观测值之间的和MRE则分别为5.03%和0.92,根据式(18)计算的re(RH)和i(RH)与其观测值之间的分别为0.70和0.85,对应的MRE则分别为1.46%和18.98%,大气能见度的计算值较观测值平均略低4.92%,其对应的和MRE分别为0.93和14.26%.其中,4种大气能见度模拟值与其观测值之间的分别为0.66,0.79,0.65和0.91, MRE则分别为10.45%,13.72%,16.59%和13.21%.可见方案三针对复折射率和粒径吸湿增长因子的建模计算结果要显著优于方案二,且针对大气能见度的建模计算效果则要显著优于方案一与方案二.

3 三种能见度计算方案的适用性分析

3.1 方案一

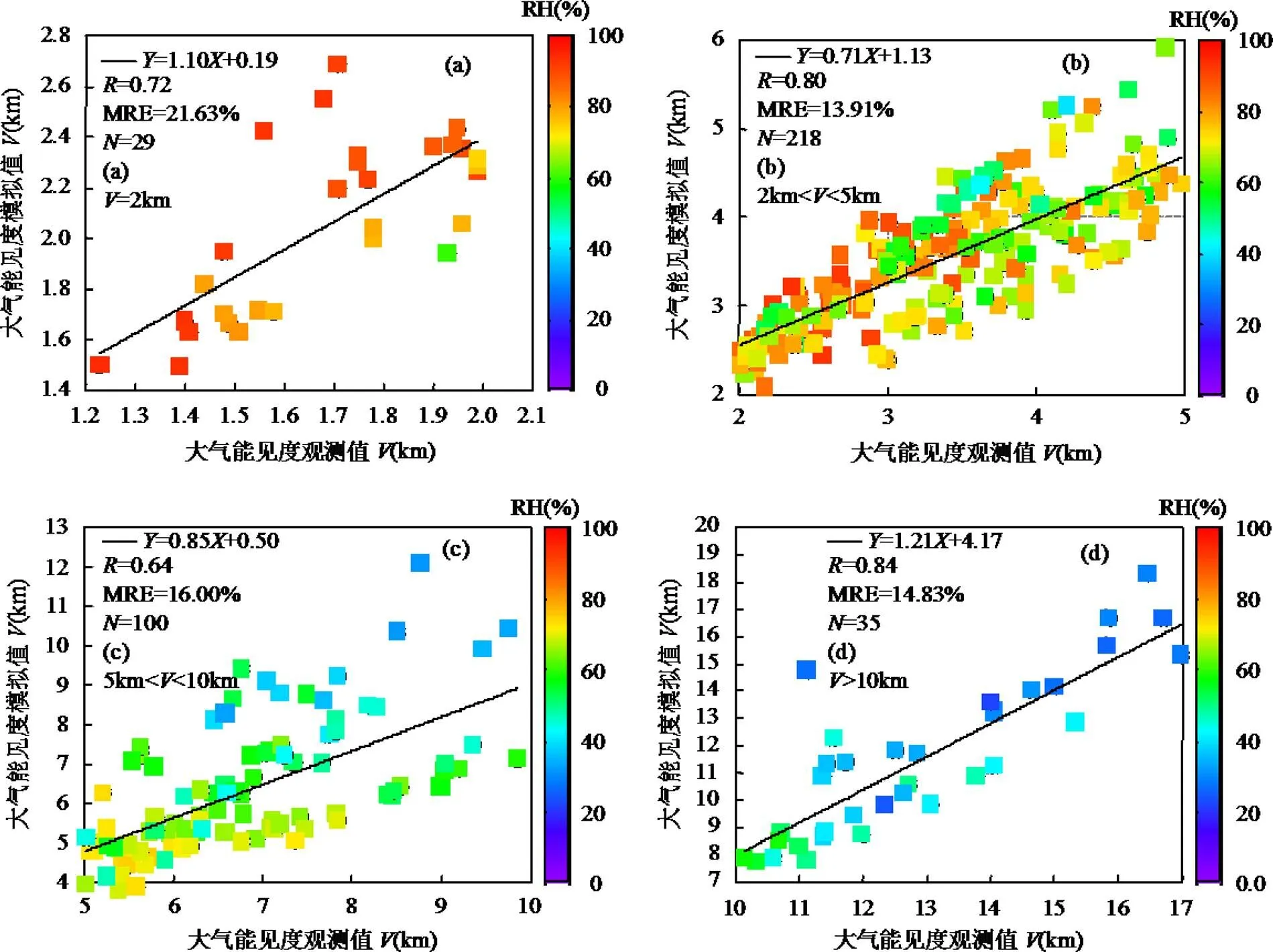
图1 不同范围大气能见度方案一模拟值与其观测值之间的对比(a: <2km; b: 2～5km; c: 5～10km; d: >10km)

基于验证数据集,根据方案一模拟了大气能见度,并分别给出了上述不同范围大气能见度模拟值与其观测值之间的散点图(图1). 模拟结果表明,4种范围(<2km, 2～5km, 5～10km以及>10km)的大气能见度模拟值与其观测值之间的分别为0.72, 0.80, 0.64, 0.84, MRE分别为21.63%, 13.91%, 16.00%, 14.83%.并随着大气能见度范围的增大,方案一的模拟效果逐渐降低,小于2km的低能见度(图1a)模拟误差最大(21.63%).结合表1与图1分析可知,小于2km的低能见度与RH之间的(, RH)为-0.35,显著大于此时大气能见度与PM2.5和BC之间的(, PM2.5)和(, BC),因此推测高相对湿度条件下气溶胶吸湿增长的不确定性可能是引起统计模型模拟大气能见度误差的重要因素.

3.2 方案二

基于验证数据集,根据方案二中re(dry)、i(dry)与的经验取值,首先根据式(18)及其=4.4的经验取值模拟获得了对应的(RH),其模拟值与观测值之间的和MRE分别为0.91和7.81%.虽然气溶胶粒径吸湿增长模型的参数为经验值4.4,但(RH)模拟值与其观测值之间的散点分布(图2)也能较好地体现不同RH条件下气溶胶粒径的吸湿增长特征,且误差尚在可接受范围之内.

图2 Gf(RH)方案二模拟值与其观测值的散点

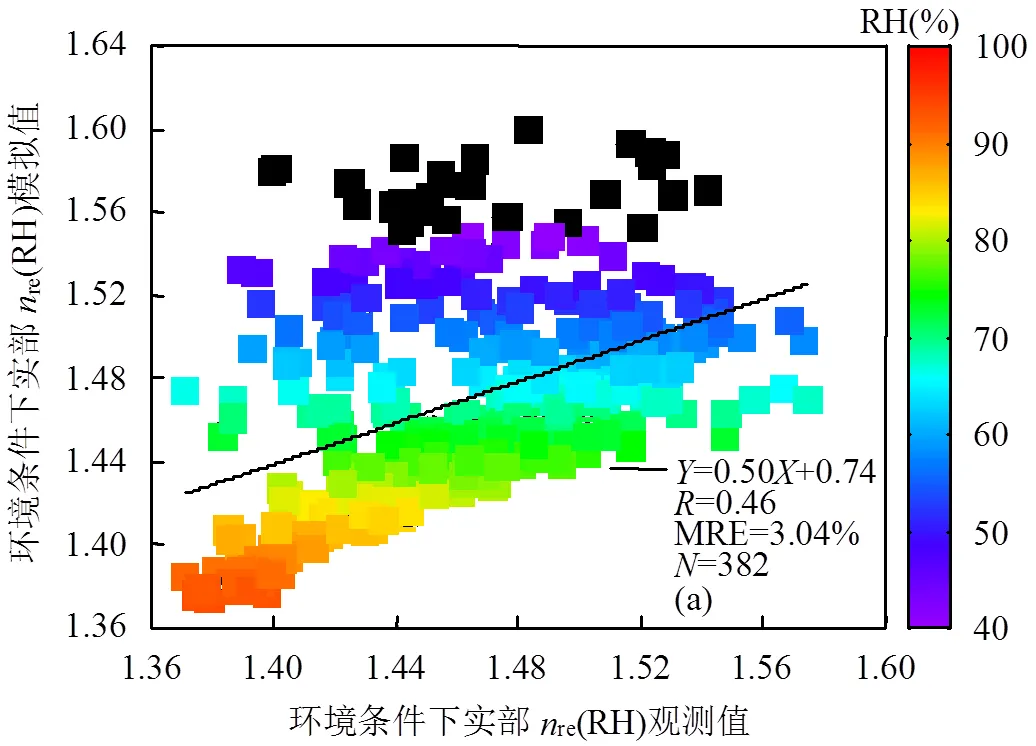
其次,re(dry)和i(dry)的经验取值与观测值之间的均为0, MRE则分别为2.79%和61.19%.在此基础上,基于前述(RH)的模拟结果,根据式(13-18))分别模拟了ACRI(图3)的re(RH)(图3c)和i(RH)(图3d),模拟结果表明,re(RH)和i(RH)的模拟值与其观测值之间的分别为0.46和0.39, MRE分别为3.04%和78.78%.从上述模拟结果可知,即使re(dry)和i(dry)为经验取值,其本身存在着很大的不确定性,但气溶胶吸湿增长之后,相应光学参数变化的不确定性也会进一步加大.另外,环境相对湿度越大,re(RH)和i(RH)与其观测值之间的相关系数也越高,表明相对湿度的增大会加强相对湿度对于折射率的决定作用.

根据前述模拟所得的(RH)、re(RH)和i(RH),依据方案二模拟获得了大气能见度,据此分别给出了上述不同范围大气能见度模拟值与其观测值之间的散点图(图4).4种范围(<2km, 2～5km, 5～10km以及>10km)的大气能见度模拟值与其观测值之间的分别为0.68, 0.91, 0.90, 0.92, MRE分别为22.79%, 25.06%, 22.85%, 12.01%.由此可见,(RH)、re(RH)和i(RH)的经验取值会导致大气能见度模拟的重大误差.另外,对比方案一和方案二的模拟结果可推测,以相对湿度作为因变量的计算ACRI和(RH)的参数化方案,在进一步结合Mie散射模型后,可更全面地表征大气能见度的非线性演变特征,而且在不主要考虑颗粒物质量浓度的本文前提下,相对湿度在大气能见度的非线性演变中起着决定性作用,因此方案二中的要显著高于方案一.当然,由于(RH)、re(RH)和i(RH)来源于相关的经验取值,这不可避免的会引起很大的模拟误差.

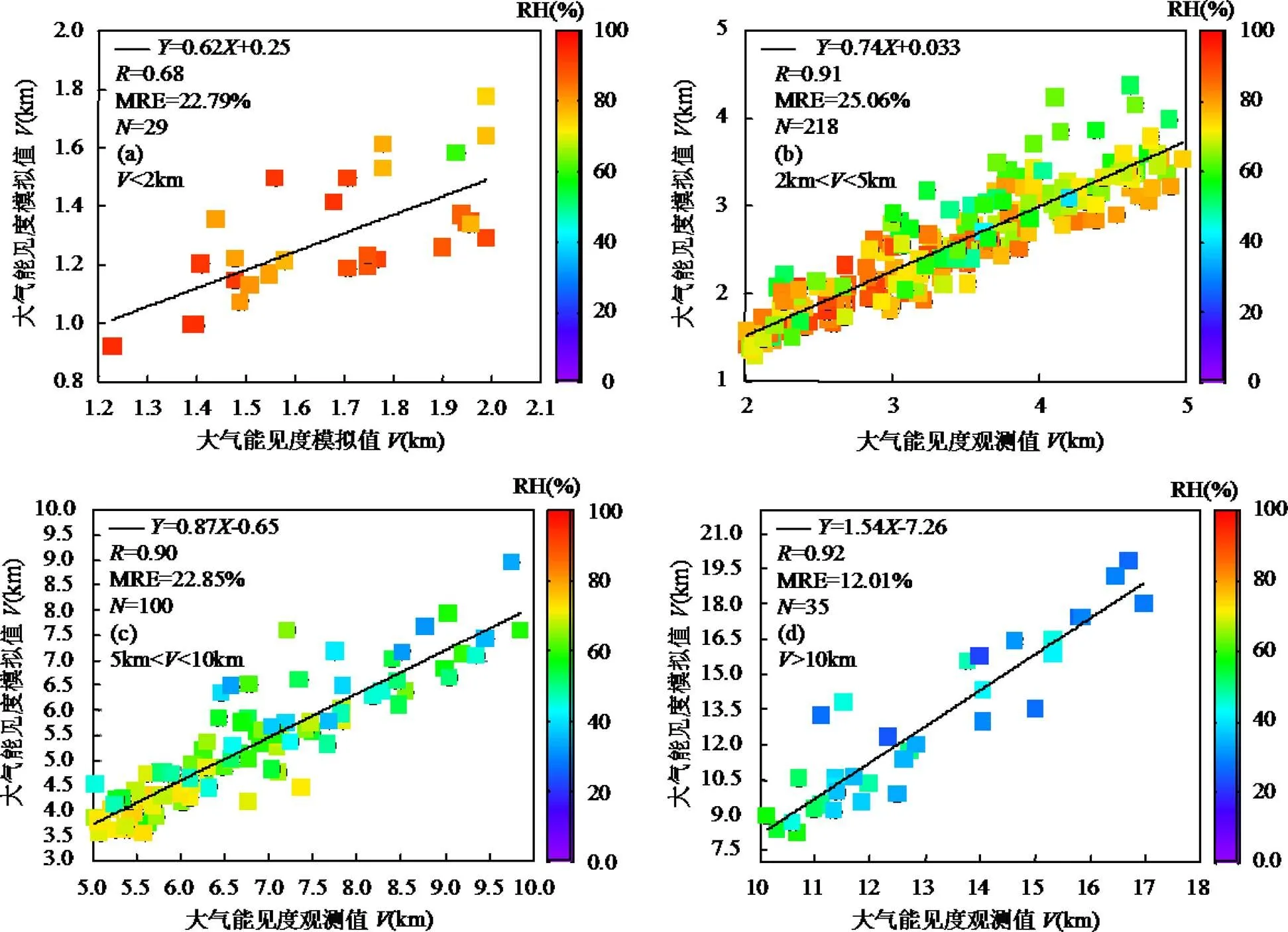
图4 不同范围大气能见度方案二模拟值与其观测值之间的对比

3.3 方案三

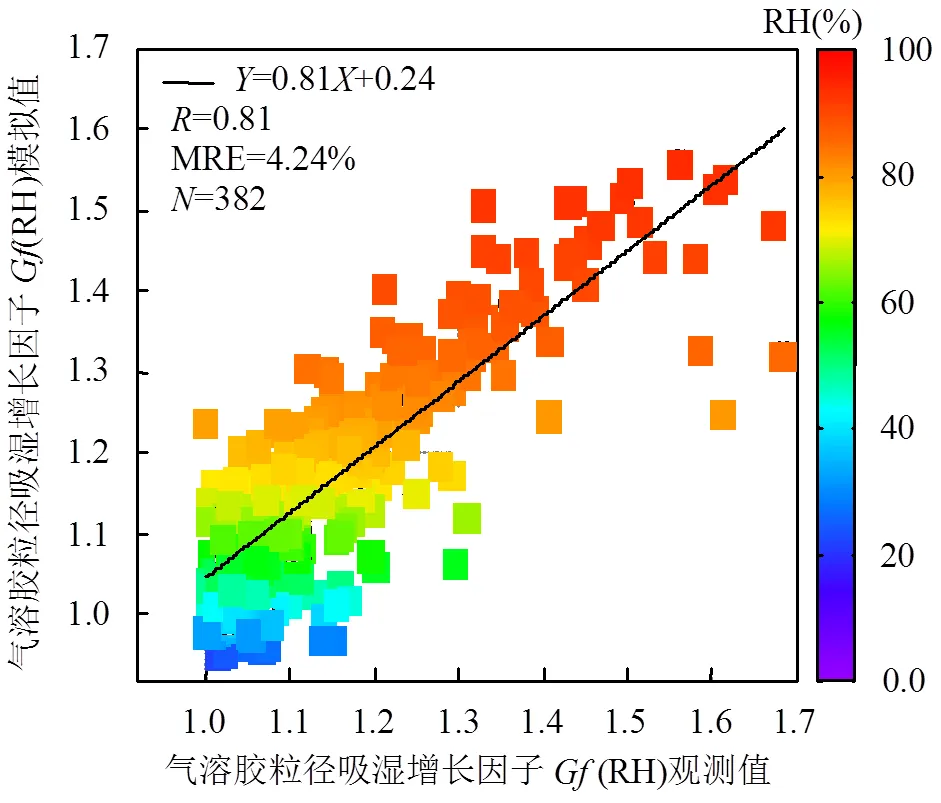
图5 Gf(RH)方案三模拟值与其观测值之间的对比

基于验证数据集,首先根据方案三中(RH)的成都秋冬季本地化参数化方案(式(21))模拟获得了验证集的(RH),其模拟值与观测值之间的和MRE分别为0.81和4.24%.相较于方案二中的经验参数化方案而言,采用本地化参数化方案模拟获得的(RH)精度更高.

基于上述(RH)的计算结果,再根据式(19)和式(20)分别模拟了干燥条件下气溶胶复折射率DACRI的re(dry) (图6a)和i(dry) (图6b),各自的模拟值与其观测值之间的分别为0.21和0.85, MRE分别为2.31%和13.36%.在DACRI和(RH)模拟结果的基础上,根据式(13～18)分别模拟了环境条件下气溶胶复折射率ACRI的re(RH) (图6c)和i(RH) (图6d),各自的模拟值与其观测值之间的分别为0.51和0.83, MRE分别为3.46%和18.84%,可见采用了本地化参数化方案的复折射率模拟效果有了显著的提升.

张智察等研究中已指出,re(dry)和i(dry)对参数化方案中自变量因子敏感程度的不同是导致两者模拟值与观测值之间和MRE存在差异的重要因素.此外,本文的DACRI参数化方案虽然可以有效地模拟出re和i,但在气溶胶化学组分信息的表征上可能仍不够精细,这很可能是导致ACRI模拟结果存在不确定性的主要原因.通过对比图6a与图6c以及图6b和图6d可知,re(dry)到re(RH)的模拟误差从2.31%提高至3.46%,对应i(dry)到i(RH)的计算误差则从13.36%提高至18.84%,这表明气溶胶的吸湿增长过程会增大ACRI,(RH)等关键气溶胶光学辐射参数的模拟误差,这一推论于方案二中针对大气能见度的模拟情况也有较好的体现,诸多研究结论也较好地验证了这一点[24,32-35].

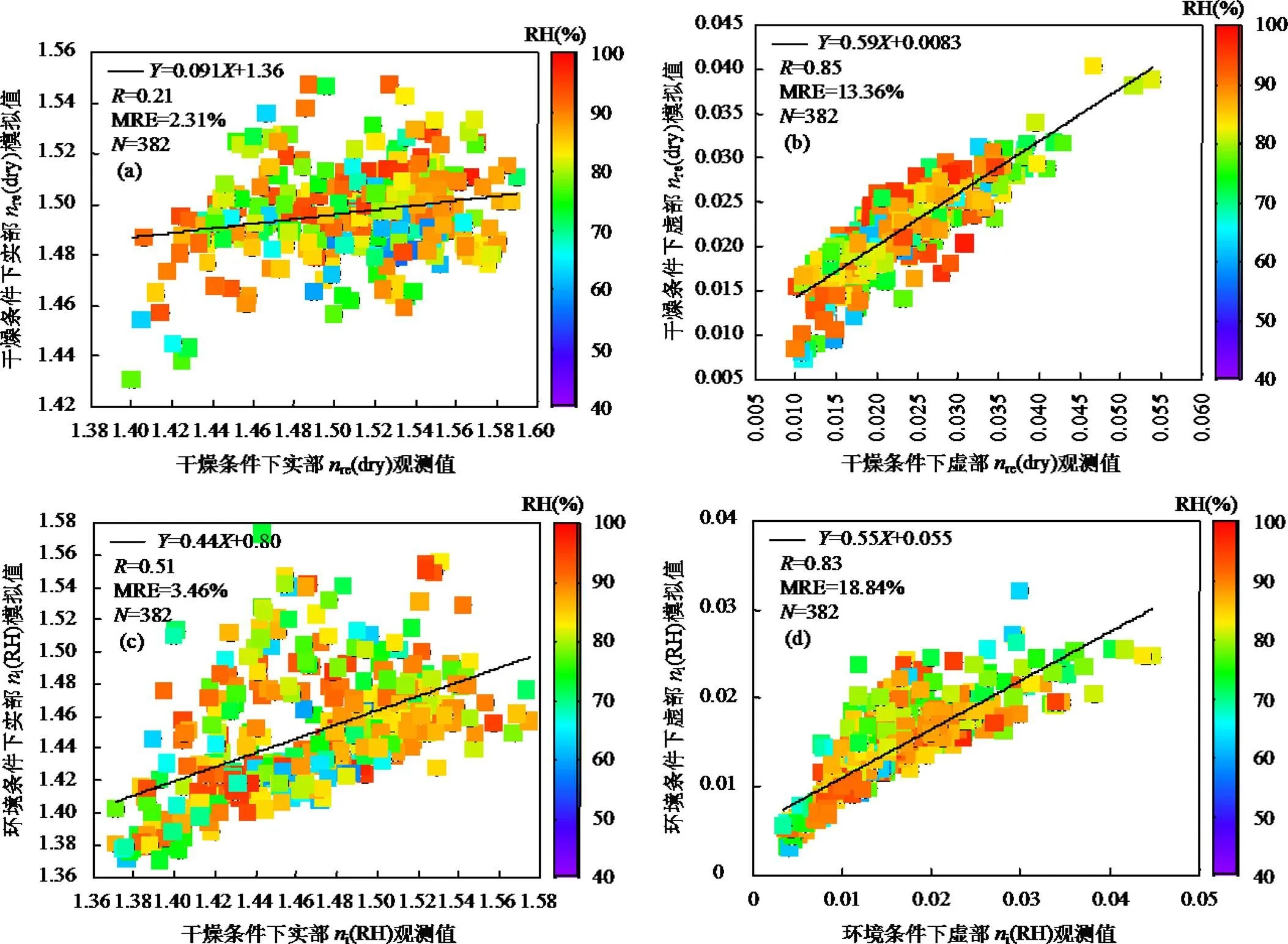
图6 ACRI方案三模拟值与观测值之间的对比

a:re(dry); b:i(dry); c:re(RH); d:i(RH)

根据前述参数化方案模拟所得的(RH)和ACRI,再依据方案三模拟获得了大气能见度,并分别给出了上述不同范围大气能见度模拟值与其观测值之间的散点图(图7). 4种范围(<2km, 2～5km, 5～ 10km以及>10km)的大气能见度模拟值与其观测值之间的分别为0.62, 0.90, 0.89, 0.93, MRE分别为9.86%, 10.39%, 9.94%, 14.06%.由此可见,较方案一和方案二而言,方案三的模拟效果在各方面均要显著占优.另外,在不主要考虑颗粒物质量浓度的本文前提下,方案三的与方案二基本一致,但模拟精度显著更优,这也表明大气能见度非线性演变特征受相对湿度的主导程度较大,光学参数的准确性则主导了大气能见度的模拟精度.

通过耦合DACRI和(RH)的成都地区本地化参数化方案来估算气溶胶光学辐射参数,并基于Mie散射模型来模拟大气能见度,最终取得了比传统方法更优的模拟效果,这反映了本文DACRI和(RH)的参数化方案在气溶胶光学辐射强迫效应模拟中的适用性.随着大气化学模式(GEOS-Chem/ WRF-Chem/WRF-CMAQ等)以及大数据机器学习算法的不断发展,目前大气污染物(BC, PM1, PM2.5, PM10and NO2),相对湿度RH以及气溶胶数浓度粒径分布()的可预报性也在不断提高,这为大气化学模式的改进提供一定参考,例如在模式的输出数据中直接运用新参数化方案估算气溶胶参数,再进行气溶胶光学辐射效应的模拟.

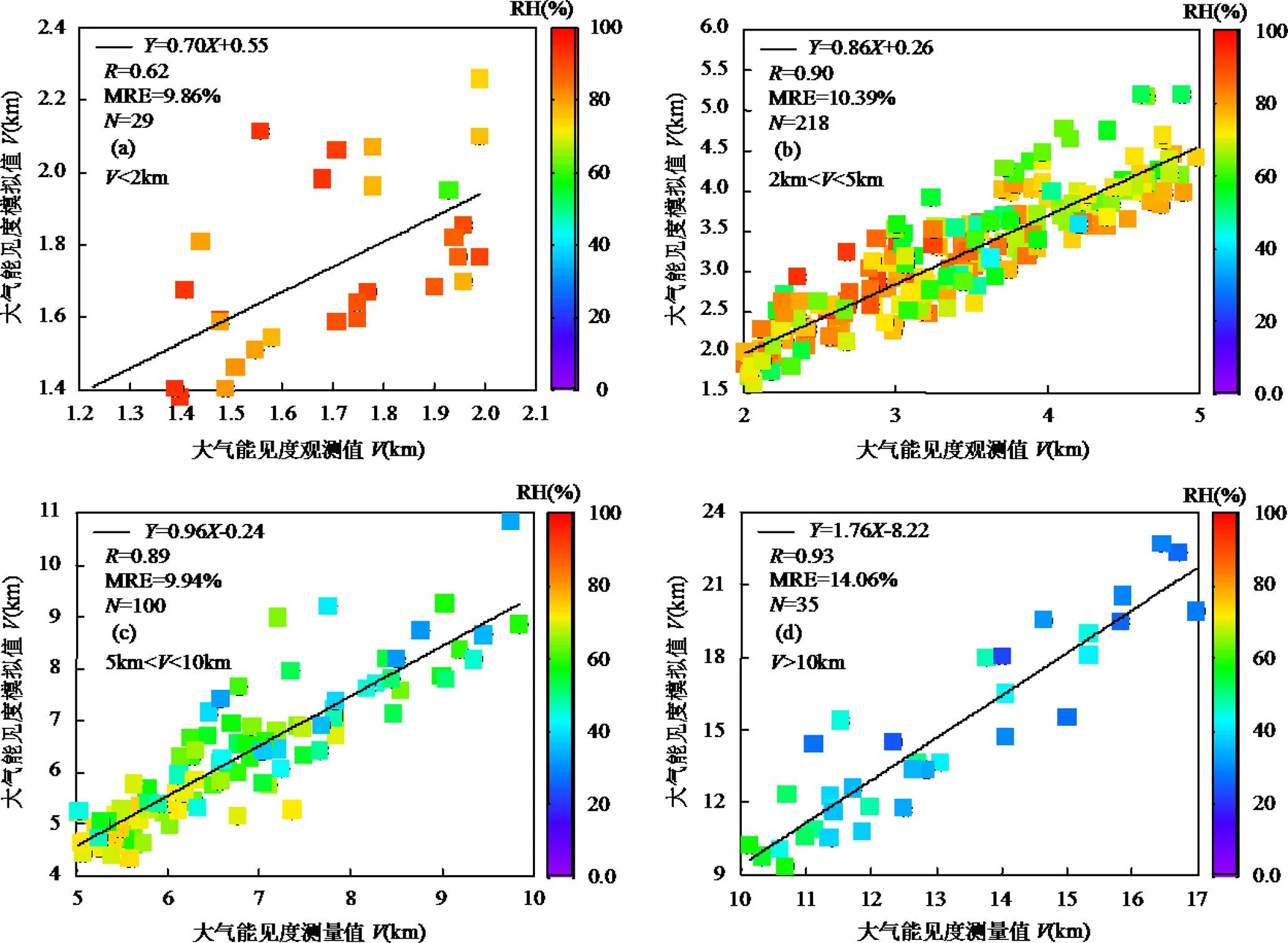
图7 不同范围大气能见度方案三模拟值与其观测值之间的对比

4 结论

4.1 经验参数的Mie散射模型、统计模型以及耦合气溶胶复折射率(DACRI)和气溶胶粒径吸湿增长因子((RH))参数化方案的大气能见度数值改进算法均能较好地模拟出能见度的变化特征.

4.2 改进算法通过本地化参数化方案更准确地估计出DACRI和(RH),从而可更准确地模拟出四类能见度区间(<2km, 2～5km, 5～10km, >10km),对应模拟值与观测值之间的相关系数分别为0.62,0.90, 0.89,0.93,平均相对误差(MRE)分别为9.86%, 10.39%,9.94%,14.06%.

[1] 张小曳.中国大气气溶胶及其气候效应的研究[J]. 地球科学进展, 2007,22(1):12-16.

Zhang X Y.Aerosol over China and their climate effect [J]. Advances in Earth Science, 2007,22(1):12-16.

[2] 吴 兑,毛节泰,邓雪娇,等.珠江三角洲黑碳气溶胶及其辐射特性的观测研究[J]. 中国科学:地球科学, 2009,(11):1542-1553.

Wu D, Mao J T, Deng X J, et al. Black carbon aerosols and their radiative properties in the Pearl River Delta region [j]. Sci. China Ser. D-Earth Sci., 2009,52(8):1152-1163.

[3] Koschmieder H. Theorie der horizontalen Sichtweite [J]. Beitrage zur Physik der freien Atmosphare, 1924:33-53.

[4] 刘新罡,张远航.基于观测的大气气溶胶散射吸湿增长因子模型研究—以2006CAREBeijing加强观测为例[J]. 中国环境科学, 2009,29(12):1243-1248.

Liu X G, Zhang Y H.Modelling research on the aerosol scattering hygroscopic growth factor based on measurement—Taking 2006 CAREBeijing campaign for example [J]. China Environment Science, 2009,29(12):1243-1248.

[5] 杨寅山,倪长健,邓 也,等.成都市冬季大气消光系数及其组成的特征研究[J]. 环境科学学报, 2019,39(5):1425-1432.

Yang Y S, Ni C J, Deng Y, et al. Characteristics of atmospheric extinction coefficient and its components in winter in Chengdu [J]. Acta Scientiae Circumstantiae, 2019,39(5):1425-1432.

[6] Pitchford M, Maim W, Schichtel B, et al. Revised algorithm for estimating light extinction from IMPROVE particle speciation data [J]. Journal of the Air & Waste Management Association, 2007,57(11): 1326-1336.

[7] Malm W C, et al. Spatial and seasonal patterns and temporal variability of haze and its constituents in the United States reports IV [R]. 2006:1-251.

[8] 马乾坤,成春雷,李 梅,等.鹤山气溶胶光学性质和单颗粒化学组分的研究[J]. 中国环境科学, 2019,39(7):2710-2720.

Ma Q K, Cheng C L, Li M, et al. The aerosol optical characteristics and chemical composition of single particles in Heshan [J]. China Environmental Science, 2019,39(7):2710-2720.

[9] 江家豪,彭 杏,朱 波,等. 深圳大气PM2.5化学组成的长期变化特征[J]. 中国环境科学, 2021,41(2):574-579.

Jiang J H, Peng X, Zhu B, et al. Long-term variational characteristics of the chemical composition of PM2.5in Shenzhen. China Environmental Science, 2021,41(2):574-579.

[10] 黄元龙.上海市大气气溶胶光学与化学性质研究[D]. 上海:复旦大学, 2014.

Huang Y L. Field studies of aerosol optical and chemical properties in Shanghai [D]. Shanghai:Fudan University, 2014.

[11] Liu X, Zhang Y, Jung J, et al. Research on the hygroscopic properties of aerosols by measurement and modeling during CARE Beijing-2006 [J]. Journal of Geophysical Research Atmospheres, 2009,114 (D00G16).

[12] 白永清,祁海霞,刘 琳,等.武汉大气能见度与PM2.5浓度及相对湿度关系的非线性分析及能见度预报[J]. 气象学报, 2016,74(2): 189-199.

Bai Y Q, Qi H X, Liu L, et al. Study on the nonlinear relationship among the visibility, PM2.5concentration and relative humidity in Wuhan and the visibility prediction [J]. Journal of Meteorology, 2016, 74(2):189-199.

[13] Chen J, Zhao C S, Ma N, et al. A parameterization of low visibilities for hazy days in the North China Plain [J]. Atmospheric Chemistry & Physics Discussions, 2012,12(11):4935-4950.

[14] Chen J, Zhao C S, Ma N, et al. Aerosol hygroscopicity parameter derived from the light scattering enhancement factor measurements in the North China Plain [J]. Atmospheric Chemistry & Physics, 2014, 14(3):8105-8118.

[15] 张智察,倪长健,邓 也,等.气溶胶等效复折射率反演的免疫进化算法[J]. 中国环境科学, 2019,39(2):554-559.

Zhang Z C, Ni C J, Deng Y, et al. Retrieval of equivalent complex refractive index of aerosol particles based on immune evolution algorithm [J]. China Environmental Science, 2019,39(2):554-559.

[16] 张智察,倪长健,邓 也,等.免疫进化算法反演均匀混合气溶胶吸湿增长因子[J]. 中国环境科学, 2020,40(3):82-89.

Zhang Z C, Ni C J, Deng Y, et al. Retrieval of hygroscopic growth factorof uniformly mixedaerosol particles based on immune evolution algorithm [J]. China Environmental Science, 2020,40(3):82-89.

[17] 周 鑫,丁菊丽,田 伟,等.能见度参数化方案概述[J]. 气象研究与应用, 2009,30(3):20-23.

Zhou X, Ding J L, Tian W, et al. introduction of visibility parameterization scheme [J]. Journal of Meteorological Research and Application, 2009,30(3):20-23.

[18] 胡 俊,赵天良,张泽锋,等.霾污染环境大气能见度参数化方案的改进[J]. 环境科学研究, 2017,30(11):1680-1688.

Hu J, Zhao T L, Zhang Z F, et al. Upgrading atmospheric visibility parameterization scheme for haze pollution environment [J]. Research of Environmental Sciences, 2017,30(11):1680-1688.

[19] Kotchenruther R A, Hobbs P V, Hegg D A. Humidification factors for atmospheric aerosols off the mid-Atlantic coast of the United States [J]. Journal of Geophysical Research Atmospheres, 1999,104(D2): 2239-2251.

[20] Bodhaine B. Aerosol absorption measurements at Barrow, Mauna Loa and the south pole [J]. Journal of Geophysical Research Atmospheres, 1995,100(D5):8967-8975.

[21] 伯广宇,刘 东,吴德成,等.双波长激光雷达探测典型雾霾气溶胶的光学和吸湿性质[J]. 中国激光, 2014,41(1):0113001.

Bo G Y, Liu D, Wu D C, et al. Two -wavelength lidar for observation of aerosol optical and hygroscopic properties in fog and haze days [J]. Chinese Journal of Lasers,2014,41(1):0113001.

[22] 李梅芳,叶芝祥.基于太阳光度计的成都双流地区夏季气溶胶光学特性研究[J]. 成都信息工程学院学报, 2014,29(2):213-216.

Li M F, Ye Z X. The studies of aerosol optical properties of Chengdu Shuangliu in summer based on the sun photometer [J]. Journal of Chengdu University of Information Technology, 2014,29(2):213-216.

[23] Penndorf Rudolf. Tables of the refractive index for standard air and the rayleigh scattering coefficient for the spectral region between 0.2 and 20.0μ and their application to atmospheric optics [J]. Journal of the Optical Society of America, 1957,47(2):176-182.

[24] Sloane C S, Wolff G T. Prediction of ambient light scattering using a physical model responsive to relative humidity: Validation with measurements from Detroit [J]. Atmospheric Environment, 1985, 19(4):669-680.

[25] 张智察,倪长健,尹单丹,等.两种气溶胶消光吸湿增长因子的适用性分析[J]. 激光与光电子学进展, 2020,57(9):090103.

Zhang Z C, Ni C J, Yin D D, et al. Applicability of the two kinds of aerosol extinction hygroscopic growth factors [J]. Laser & Optoelectronics Progress, 2020,57(9):090103.

[26] 陈一娜,赵普生,何 迪,等.北京地区大气消光特征及参数化研究[J]. 环境科学, 2015,36(10):3582-3589.

Chen Y N, Zhao P S, He D, et al. Characteristics and parameterization for atmospheric extinction coefficient in Beijing [J]. Environmental Science, 2015,36(10):3582-3589.

[27] Bohren C F, Huffman D R. Absorption and scattering of light by small particles [M]. John Wiley & Sons Inc. 1983.

[28] 沈建琪,刘 蕾.经典Mie散射的数值计算方法改进[J]. 中国粉体技术, 2005,11(4):45-50.

Shen J Q, Liu L. An improved algorithm of classical Mie scattering calculation [J]. China Powder Science and Technology, 2005,11(4): 45-50.

[29] 孙景群.湿气溶胶的光散射特性[J]. 高原气象, 1983,2(3):49-54.

Sun J Q. Relationship between visibility and relative humidity [J]. Plateau Meteorology, 1983,2(3):49-54.

[30] 孙景群.能见度与相对湿度的关系[J]. 气象学报, 1985,43(2):230- 234.

Sun J Q. The relationship between visibility and relative humidity [J]. Journal of Meteorology, 1985,43(2):230-234.

[31] Kasten F. Visibility forecast in the phase of pre-condensation [J]. Tellus, 1969,21(5):631-635.

[32] Ycc A, Rws A, Ghm A, et al. Source apportionment of visibility degradation problems in Brisbane (Australia) using the multiple linear regression techniques [J]. Atmospheric Environment, 1999,33(19): 3237-3250.

[33] Ebert M, Weinbruch S, Rausch A, et al. The complex refractive index of aerosols during LACE 98 as derived from the analysis of indivi-dual particles [J]. Journal of Geophysical Research: Atmospheres, 2002,107(D21):LAC 3.

[34] Wex H, Neusü C, Koziar C, et al. Particle scattering, backscattering, and absorption coefficients: An in situ closure and sensitivity study [J]. Journal of Geophysical Research Atmospheres, 2002,107(21):LAC 4.

[35] Cheng Y F, Eichler H, Wiedensohler A, et al. Mixing state of elemental carbon and non-light-absorbing aerosol components derived from in situ particle optical properties at Xinken in Pearl River Delta of China [J]. Journal of Geophysical Research Atmospheres, 2006,111(20): 4763-4773.

An improved numerical algorithm for simulating atmosphere visibility by coupling two aerosol parameterization schemes.

ZHANG Zhi-cha1,2, NI Chang-jian1*, ZHAO Jun-ping2, FENG Miao3, XIE Yan-xin1, WANG Yang-fei1

(1.School of Atmospheric Sciences, Chengdu University of Information Technology, Chengdu 610225, China；2.Zhejiang Meteorological Observatory, Hangzhou 310017, China；3.Chengdu Academy of Environmental Sciences, Chengdu 610072, China)., 2021,41(11)：5009～5018

Based on the Mie theory, an improved numerical algorithm for simulating atmosphere visibility was proposed by coupling the parameterization schemes of aerosol complex refractive index (DACRI) and aerosol hygroscopic growth factor(RH). By utilizing the monitored data at an hourly time step recorded by WS600 integrated weather station, AURORA-3000 integrating nephelometer, AE-31aethalometer and GRIMM180 environment particle monitors from October to December in 2017 in Chengdu, the applicability of the improved algorithm was futher evaluated by compared with those of two visibility calculation methods, which are Mie theory model with empirical parameters and statistical model, in different visibility intervals (<2km, 2～5km, 5～10km, >10km). The results show that the three visibility calculation methods can capture the variation characteristics of visibility well; The improved algorithm better simulate visibility by adopting localization parameterization schemes to estimate DACRI and(RH). The corresponding correlation coefficients () between the simulation and the observation are 0.62, 0.90, 0.89, and 0.93, respectively. The mean relative error (MRE) are 9.86%, 10.39%, 9.94%, and 14.06%, respectively.

aerosol；complex refractive index；hygroscopic growth factor；parameterization scheme；visibility

X513

A

1000-6923(2021)11-5009-10

张智察(1995-),男,浙江丽水人,成都信息工程大学硕士研究生,主要从事大气物理学与大气环境方面研究.发表论文7篇.

2021-03-30

国家重点研发计划项目(2018YFC0214004;2018YFC1506006);四川省科技厅应用基础研究(2021YJ0314)

* 责任作者, 教授, ncj1970@163.com