保持稀疏重构的半监督字典学习在扶梯场景下的应用

王国庆 邵卫华 李克祥 夏文培 陈林林

（浙江索思科技有限公司，浙江 温州 325000）

0 引言

近年来，随着中国经济的高速发展，社会城镇化水平也不断提高，电扶梯作为在公共场所运输行人和物品的重要工具之一，其保有量逐年增加，越来越多的电扶梯被应用于车站、商业建筑和旅馆等场所，已成为生活中不可或缺的部分。复杂场景下人的运动跟踪与行为理解研究已经成为一个极具吸引力的探索方向，该文针对电扶梯的应用场景，研究了保持稀疏重构的半监督字典学习方法，并进行了实际场景下人体检测的实验，为后续异常行为分析奠定基础。

1 保持稀疏重构的半监督字典学习

为了解决因噪声和遮挡而导致运动区域出现人体误判的问题，该文拟根据数据本身之间的稀疏结构关系，利用半监督的方法学习人体与其他运动目标具有区分性的模板字典，实现对模板字典的在线更新，同时也为下面人体的鲁棒跟踪提供了可靠的模板。稀疏表示理论表明，如果每类样本都足够充分的话，那么每个样本都倾向于能用其所在的类别中的其他样本线性来表示，而且这种表示方式是稀疏的。此外，同一类样本共享少量的字典模板，这些字典模板反映了该样本的本质特征。采集一些先验的人体样本作为正样本，将这些样本所组成的集合记为X+，检测到的运动区域样本为无标签样本Xunlabel，随机采集到的背景样本集合记为X-。 记X=[XunlabelX+X-]，X（X为样本集合。）在当前字典D下的稀疏表示矩阵为A=[AunlabelA+A-]（Aunlabel为无标签集合；A+为正样本；A-为负样本）。记G为原始数据的稀疏重构系数矩阵，即G的第i行表示样本xi在X中的稀疏重构系数（其中要求xi不能用它本身来表示，即gii≠0，第i行的稀疏重构系数不能为0。则建立以下优化问题，如公式（1）所示。

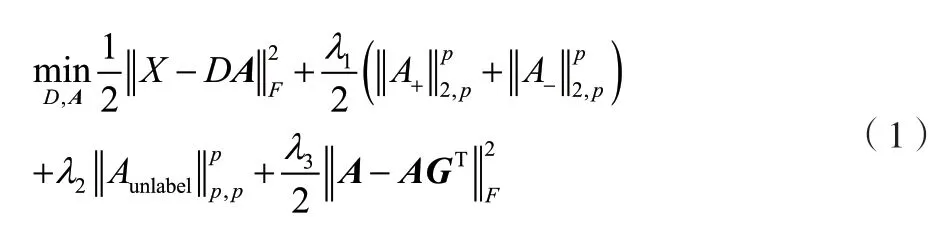
式中：D为字典；F、p为稀疏系数；λ为特征值。

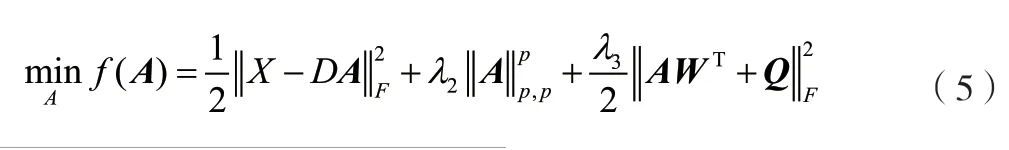
为了求解上述优化问题，引入函数（如公式（6）所示）（其中A0为A的初始值；J（A，A0）为定义的一个优化函数；H为定心矩阵回归系数，（η1、η3为λ系数里的分母部分；λ3为λ系数里的分母部分）。则A的求解可通过如公式（7）所示的迭代进行求解（λ、H如公式（8）、公式（9）所示）。

式中：J（A，Ak）为函数的迭代计算。

公式（7）可通过软阈值方法获得解析解。

2 稀疏重构

2.1 稀疏编码

稀疏编码（Sparse Coding）是指找到图像块在当前字典下稀疏表示系数的过程，即稀疏分解。字典的训练速度性能与稀疏编码过程的 优劣有直接关系，会影响图像的重构效果。

2.1.1 基于稀疏重构的字典训练算法

完备字典构造方法可分2类：非自适应字典学习和自适应字典学习[1]。非自适应字典是通过数据模型得到的，其计算速度比较快，但字典结构一般固定不变，稀疏表示信息的能力有限。自适应字典学习方法可以选择建立训练样本，然后在该样本集的基础上学习得到一个字典，该字典对信号的表示也更为稀疏、简洁。字典学习问题的优化稀疏性约束方法，如公式（9）所示。

式中：D为训练数据集，D=（x1，x2，...，xn）∈Rm×n（矩阵对每一数据表示权重为X=（a1，a2，...，an）∈Rm×K）；x为定心矩阵回归系数；s、t为矩阵值正则化参数；y为原始样本；Dx为查字典过程的矩阵乘法表示；ε为任意极小正数。

也可表示为公式（11）。

式中：||X||0为l0范数，即X中非零值的个数；T0为非零数目的最大值。

采用光流算法[2]结合稀疏重构对通过一段‘港龙鹰眼’捕获到的一段汽车视频进行实验，对比实验情况可见，结合稀疏重构算法后，对运动目标的检测更加准确，汽车捕捉数量明显增多，如图1所示。

图1 稀疏重构算法对比实验

2.2 半监督学习实验

使用行人数据训练集1 750张，；测试集数据270张，其中标注数据为70张。先用有标签的数据训练网络，提取该网络中所有数据的特征，进而以这些特征为依据，采用SVM算法[3-4]对无标签数据进行分类，同时将认为分类正确的数据拣入数据集，再重新进行网络训练。通过循环训练，已标注的数据逐渐增加，分类器的效果逐渐得到提升。下面列出了在半监督学习数据集上对监督学习算法的评估并给出了实验场景，运行算法模型拟合带有标注的训练数据集，同时在测试数据集上对其进行评估。

2.2.1 生成算法

2个样本集合：L={（xi，yj）}和U={xj}，L=Llable，表示有标注样本；U=UNlabel，表示无标注样本。

对有标注数据集L={（xi，yj）}ij和无标注数据集U={x}1+uj=l+1进行 以下操作：1）使用监督学习从L中训练F模型。2）将F模型应用于U中未标记的实例。3）从U中删除一个子集S，将{（x，f（x））|x∈s}加入L。4）重复上述操作直到U为空集。

算法中用欧式距离来定义表现最好的无标记样本，再用F模型对其进行标记，将标记的数据加入L中，同时对F模型也进行动态更新。

2.2.2 半监督SVM支持向量机生成模型

半监督SVM支持向量机[5]生成算法模型为f（x）=wTx+b。

首先，对二分类问题进行讨论，即定义y{-1，1}，其特征空间为RD，决策边界的定义如下{x|wTx+b=0}（w为决定决策边界方向和尺度的 参数向量；wT为模型参数转置；b为偏移量参数 ）。如图2所示，定义w=（1，1）T，b=-1，可得决策边界实线a，由图2可知，决策边界总是与w向量垂直的。

其次，算法模型为f（x）=wTx+b，决策边界是f（x）=0，通过sign（f（x））来预测x的标签，计算实例x到决策边界的距离，例如原点x=（0，0）到决策边界的距离为|f（x）|/||w||，如图2中的实线b。定义有标签实例到决策边界的有符号距离为1/ 2≈0.707。

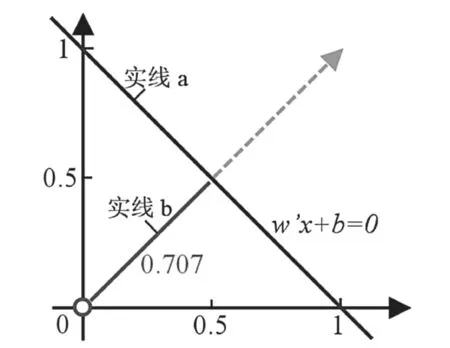
图2 决策边界线

上述得出的标签预测器sign（f（x）），对无标签样本，其预测标签为sign（f（x）），假定该预测值就是x的标签，那么就可以直接在x上应用hinge损失函数如公式（12）所示。

由于标签是用f（x）生成的，因此无标签样本总是能被正确分类，然而hat loss仍然可以惩罚一定的无标签样本。从公式（12）中可以看出，hat损失函数更偏爱f（x）≥1orf（x）≤-1（惩罚为0，离决策边界比较远），而惩罚-1＜f（x）＜1（特别是趋近于0）的样本可能会被错误分类。这样可以写出S3VMs在有标签和无标签数据上的目标方程，如公式（13）所示。

经上述推导的结果是不平衡的（大多数甚至所有的无标签数据可能被分为一个类），一种修正该错误的启发式方法就是在无标签数据上限制预测类的比例与标签数据的比例相同（如公式（14）所示）。

式中：为有标签样本；yi为无标签样本。

由于是不连续的，很难满足这个约束，因此对其进行松弛，转化为包括连续函数的约束，如公式（15）所示。

最后，如果仅使用有标签数据学得的决策边界将穿过密集的无标签数据，但如果假定2个类是完全分开的，那么期望的决策边界可以很好地将无标签数据分成2类，而且也正确地对有标签数据（虽然它到最近的有标签数据的距离比SVM小）进行分类。

通过上述公式的推导，将半监督SVM算法训练与监督算法训练进行比较，如图3所示。图3（a）表示监督学习进行迭代训练4次，精确度达到0.8618，图3（b）表示采用半监督学习进行迭代训练5次，精确度达到0.9186，可以达到比较好的效果。

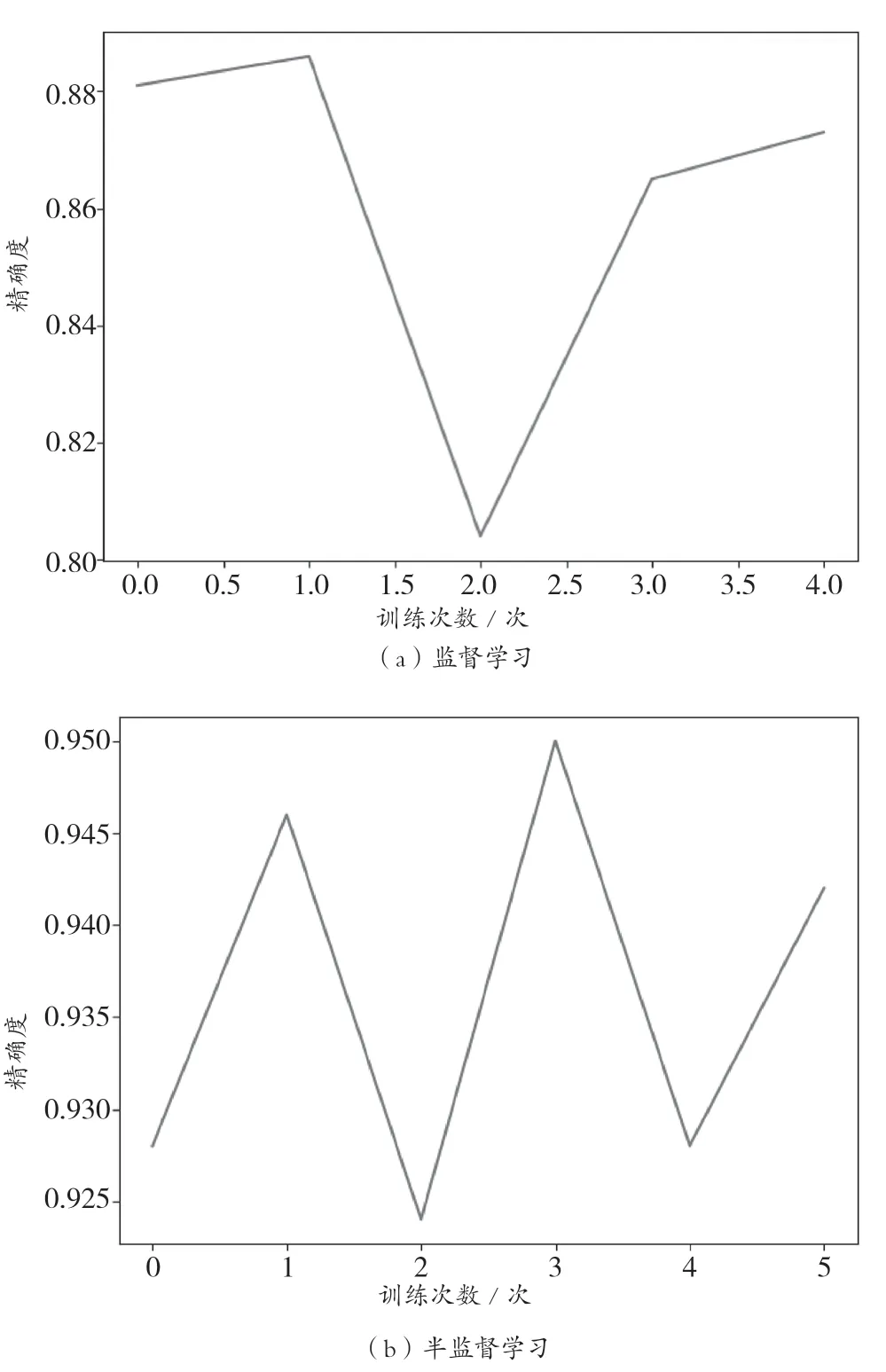
图3 训练比较

2.3 扶梯场景实验：人体捕捉

综合上述算法得出的结论，使用手扶梯摄像头拍摄场景视频输入，结合深度学习卷积神经网络准确、快速地捕获人体目标，从而实现目标检测。

步骤一：获取视频输入得到每帧图像数据，创建背景模型内核函数。在整个算法中由于需要对视频帧进行相关操作，这里需要初始化定义帧的变量。

步骤二：转换帧为灰白图，也就二值化操作。对图像进行均值滤波高斯[6]模糊处理，并使用背景差法，以移除灰色值。

步骤三：进行形态运算，先创建轮廓列表用于存放目标轮廓，判断目标轮廓 是否满足阀值，添加轮廓列表进行排序找到最大轮廓。确定最大轮廓的坐标值和数量，设置一个数组来存储最近的目标轮廓边界值。跟踪最近目标轮廓边界索引值，比较两轮廓包围的接近程度进行合并。调用最接近函数进行检测找到关闭盒子的极限值。存储对角线的点值，找到最近线边界线的极限值。

步骤四：列出所有目标轮廓并画出目标，如图4所示。

图4 人体检测

3 结论

在视觉算法目标检测领域，图像数据的不足是影响目标检测精确的主要根源，稀疏重构的半监督字典学习算法理论在目标运动跟踪中共享少量的字典模板，这样就将无标签样本的信息也融入优化问题中。实验所采用的算法虽然在运行目标捕获中有一定成效，但是仍然存在不足。例如在捕获运动目标时不能做出分类预测。目前也正在验证与CNN、GAN以及RNN等相关深度神经网络结合的可行性，以期使该算法发挥出最大的优势。