基于状态空间MPC的无人机无人车联合运动控制*
2021-12-01周锐森冯友兵
周锐森 冯友兵
(江苏科技大学电子信息学院 镇江 212003)
1 引言
无人机无人车联合运动作为异构智能体协同运动控制重要组成部分[1],受到国内外普遍关注。无人车在危险、肮脏环境下的救援运输能力与无人机在灾情探测、搜救、检查的能力具有很强的互补性,二者协同可以有效拓宽UAV以及UGV的应用范围,在军事和民用活动中都具有很大的实用价值[2]。
当前无人器联合运动方法主要有基于行为法、虚拟结构法、人工势场法、领导-跟随法等。文献[4]基于反步法运用行为法生成虚拟机器人实现无人车的联合运动控制;文献[5]根据领导-跟随法基于Lyapunov方法设计状态观测器实现多无人机的联合运动跟踪控制。其中一致性算法已经有大量研究[6~7],比如文献[3]基于虚拟结构法将自适应拓扑通信与一致性算法相结合实现多无人机的联合运动控制,可是一般都只是将联合运动的成员看作质点忽略其模型运动特征,在建立了无人器非线性模型后根据位置速度误差得到控制率。却忽略了模型本身运动中姿态控制的约束问题,虽然有学者提出基于hp自适应伪谱法的控制[8],但约束只考虑到转换矩阵中欧拉角奇异值问题而忽略实际工程中的物理意义。在实际工程中,不论是四旋翼无人机还是无人车都会因为控制输入量过大或者对其变化率过大,造成无人器过分响应导致飞机翻机坠毁、无人车失联等问题。
模型预测控制可以将运动系统实际的约束条件加入预测运动中,实现最优控制。Ahmed Hafez等[9~10]提出一种基于模型预测控制的无人机无人车联合运动方案,相比其他方法能够更好的控制对智能体运动的约束。本文参考相关文献并结合实际工程的经验,在满足无人机无人车联合运动的要求下,对无人机无人车模型分别进行各自要求解耦变化得到符合实际无人机无人车联合运动的四旋翼无人机状态空间模型以及无人车模型。并引入虚拟领航者作为领导者,各个智能体在联合运动位置要求下将领导者轨迹几何计算得到各自参考轨迹,完成联合运动。
2 四旋翼无人机与无人车的非线性动力学模型转化
2.1 四旋翼无人机非线性动力学模型线性化变换
如图1所示,惯性坐标系为OE—XEYEZE,OB—XBYBZB为机体标系。建立准确的无人机模型是设计控制器关键,为便于求解,对模型做出下列假设:
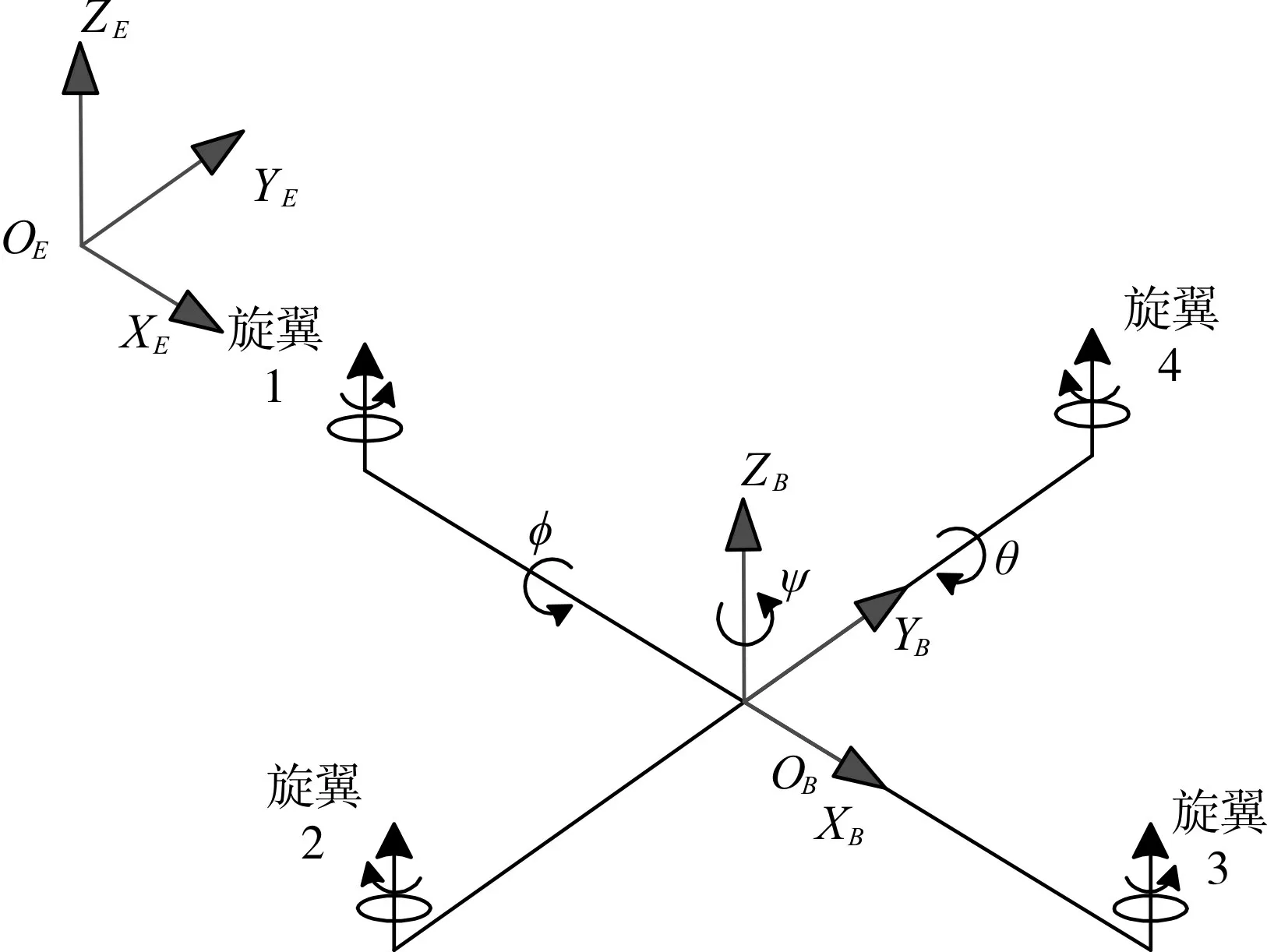
图1 四旋翼结构示意图
1)四旋翼是刚体;
2)四旋翼质量转动惯量不变;
3)四旋翼重心和几何重心一致。
其中四旋翼无人机质量为m;重力加速度为g;设[Vx Vy Vz]T为惯性坐标系下的速度矢量;[x y z]T为无人机惯性坐标系下的质心位置;[Фθ Ψ]T为无人机机体坐标系下姿态角分别为滚转角、俯仰角、偏航角。
利用Newton-Euler法[13]忽略空气阻力可将动力模型描述为
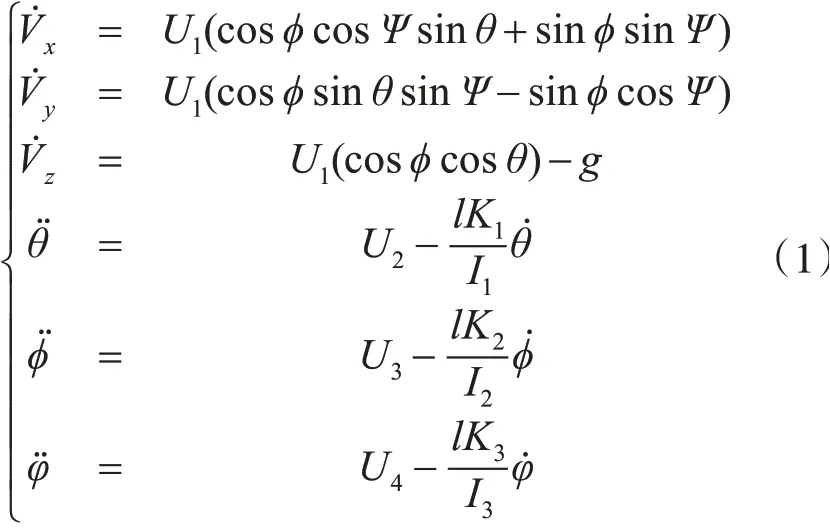
式中U1为四旋翼无人机升力输入;U2、U3、U4为姿态控制输入量,由下级PID姿态控制飞控控制;l为每个旋翼末端到飞行器重心距离;Ii为每个轴转动惯量;Ki为阻力系数。
一 般 将U1(cosФcosΨsinθ+sinФsinΨ)、U1(cosФsinθsinΨ)以及U1(cosФcosθ)当做XYZ轴的输入UXUYUZ独立设计其控制率[14],并把UXUYUZ作为下级姿态控制量解算欧拉角。然而这样在实际工程中很难得到XYZ轴位移与各个欧拉角的直接关系;同时由于耦合的关系,它们相互影响也很难使得所谓控制率能够精确实现;在实际工程的模型预测控制中无法对应找到准确的输入约束。但是由于无人机无人车联合运动的特殊性,可进一步变形:
1)设置无人机在固定高度,所以不需要Z轴变化,Z轴的合力为0,速度以及加速度都为0:
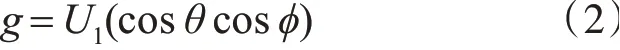
2)在很多参考文献,如文献[4]~[5]都有预先限定偏航角完成四旋翼无人机运动控制,所以可以限定偏航角为0并带入原先模型,于是可得:
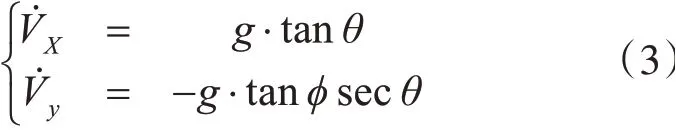
将gtanθ和-gtanФsecθ作为新的输入UXUY。
综合式(1)~(3)可以得到联合运动控制中无人机状态方程:
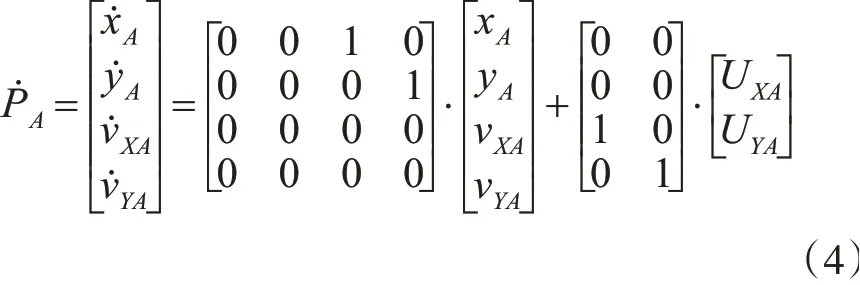
其中PA=[xA yA vXA vYA]T是无人机位置速度矢量,UA=[UXA UYA]T为无人机输入控制量,其对应的姿态控制量为滚转角φ,俯仰角θ。
2.2 无人车运动模型
由于无人车为一阶运动系统较为简单,本文无人车采用两轮差速运动,假设单位时间内左右轮位移分别为Δl和Δr,两轮之间距离为d,无人车的角度变化为ω,线速度变化为V。则有:
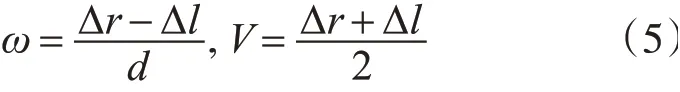
不考虑电机驱动动态性能对无人车影响,不考虑车内部摩擦、阻尼对系统影响。运动学方程为
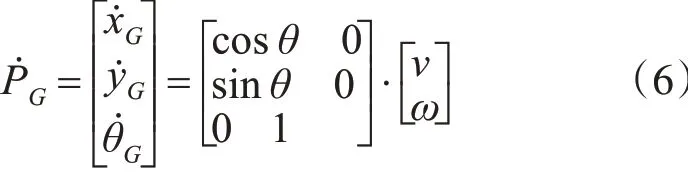
其中PG=[xGyGθG]T是无人车质心M在惯性坐标系下的位置矢量包括坐标以及航向角,输入为线速度v、角速度ω。
3 控制器设计
3.1 控制策略
以领导者-跟随者为控制策略,如图3通过引入虚拟领航者,假设一个虚拟点为虚拟领航者提供领航者的运动轨迹和实时速度,跟随者无人机与无人车通过接收到领航者位置后几何解算得到期望轨迹,并作为跟随者的参考轨迹输入无人车无人机的MPC联合运动控制器。
图2 联合运动策略示意图
虚拟领航者策略一方面能够解决由于领航者故障导致整体联合运动失控问题,另一方面可以设计准确的控制率得到每时每刻的准确轨迹与速度,为模型预测中求解优化提供准确的参考输入,设虚拟领航者状态空间方程为
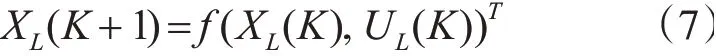
领航者的状态量为XL(K)=[xL(K),L(K)]T,输入量为UL(K)=[VXL(K),VYL(K)]T,输出为YL(K)=[xL(K),yL(K),VXL(K),VYL(K)]T。无人器通过联合运动队形要求,根据虚拟领航者提供的状态信息生成参考轨迹用于模型预测控制中的滚动优化求解。将优化求解的控制量作用于控制对象以及对应模型。
设YRA(K)=[xRA(K),yRA(K),VRAX(K),VRAY(K)]T为无人机接收虚拟领航者信息后为满足队形需求保持距离几何计算得到的参考轨迹输入,YRG(K)=[xRG(K),yRG(K),VRGX(K),VRGY(K)]T为无人车接收虚拟领航者信息后几何计算的参考轨迹输入,与传统轨迹跟踪不同,为了满足联合运动控制效果,提取速度信息为参考轨迹元素,可以提高联合运动的动态效果。控制器通过滚优化得到输入控制率完成无人机无人车联合运动控制。
由于无人车为一阶系统,速度本为输入量。为了提高运动中实时跟随效果,对传统无人车运动状态空间模型变化得到增广模型设计对应MPC控制器。而无人机虽然为二阶运动模型,但是又分为外环轨迹运动控制与内环姿态控制,本文内环姿态控制使用传统PID控制器,并按照工程实际要求对其设置姿态角输出限幅,控制器结构示意图如图3。
3.2 四旋翼无人机姿态控制
姿态控制模型可以简化为
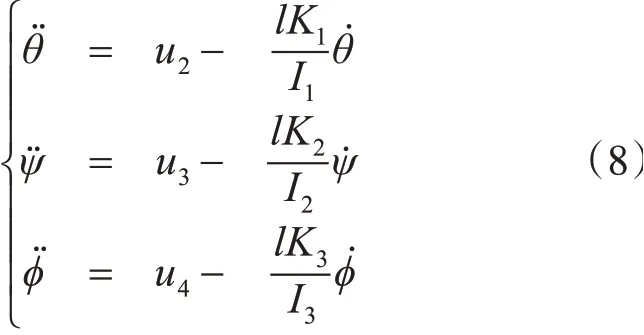
[Фθ Ψ]T为机体坐标系下姿态角分别为滚转角、俯仰角、偏航角;u2、u3、u4为姿态控制输入量,由PID姿态控制飞控控制;l为每个旋翼末端到飞行器重心距离;Ii为每个轴转动惯量;Ki为阻力系数。其PID较为简单也并非本文主要研究内容,在此不再赘述。
3.3 四旋翼无人机位置运动状态空间模型
对式(5)离散化,假设采样时间为T得
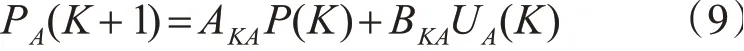
式中:
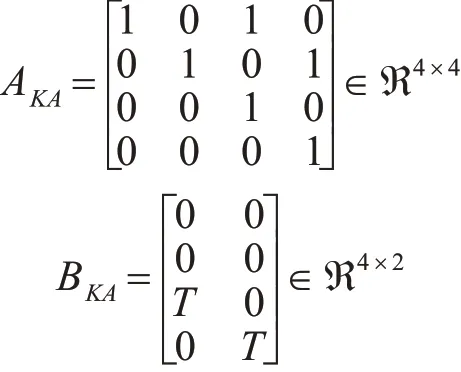
定义无人机联合运动增广状态矩阵为
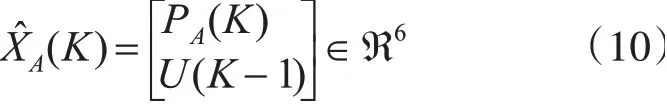
可得增广状态空间模型为
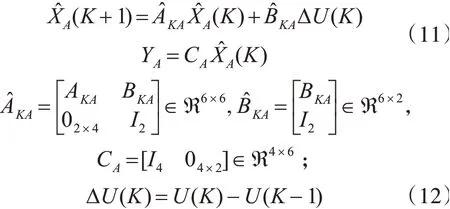
设NPA为预测步长,NCA为控制步长,在任意采样时刻K,离散状态输出可表示为
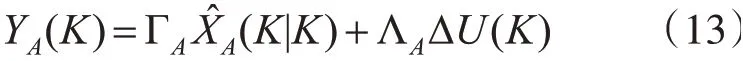
其中:

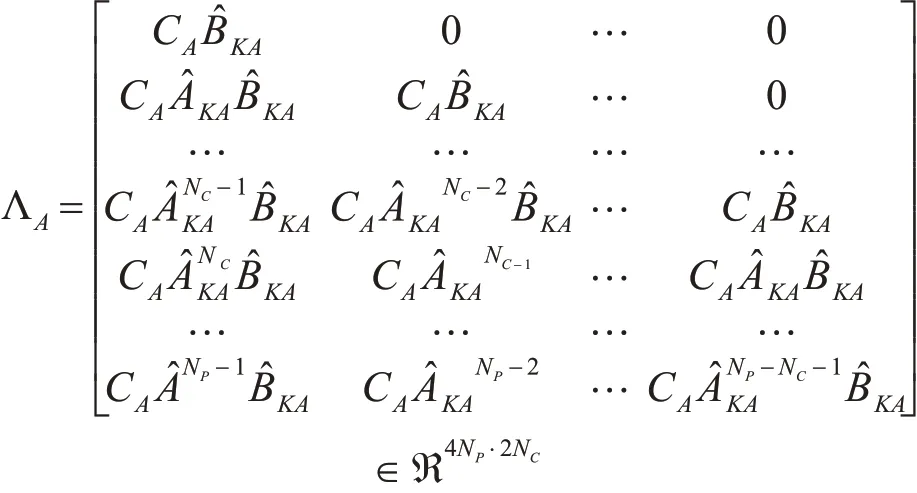
3.4 无人车位置运动状态空间模型
首先假定一个针对无人车模型的参考轨迹微分动态为
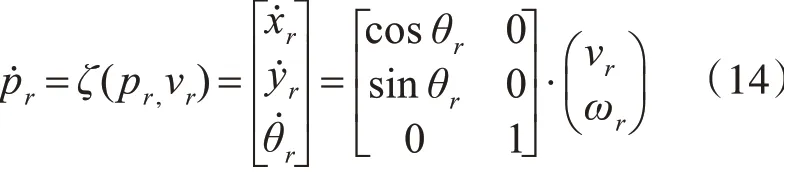
其中Pr=[xryrθr]T为假定参考轨迹。
利用泰勒公式局部线性化,把方程在参考轨迹点(pr,vr)处展开得到
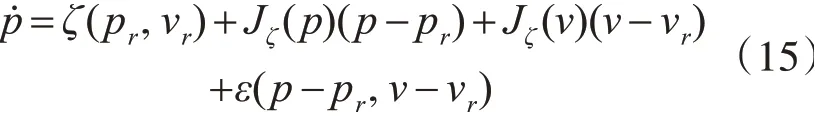
其中ε(p-pr,v-vr)为高阶余项可以忽略不计,而和分别为ζ(p,v)相对于P和v的雅可比矩阵。将方程(14)与方程(15)相减可得线性状态误差方程为
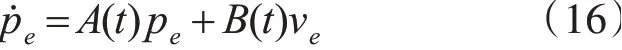
但是实际中无人车的参考信息是离散形式YRG(K)=[xRG(K),yRG(K),VRGX(K),VRGY(K)]。可以用其反向表示处所需要的假定领航者信息,对式(16)离散化,假设采样时间为T得:
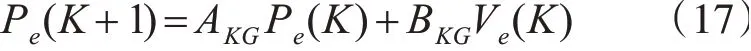
其中:

定义联合运动增广状态矩阵为
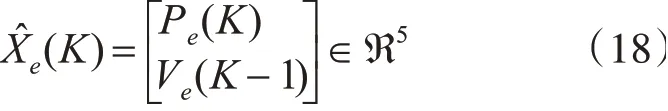
可得增广状态空间模型为
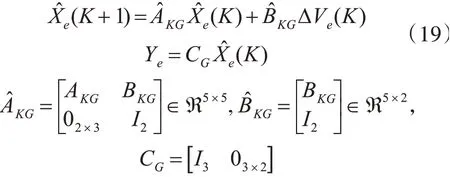
设NPG为预测步长,NCG为控制步长,在任意采样时刻K,离散状态输出可表示为
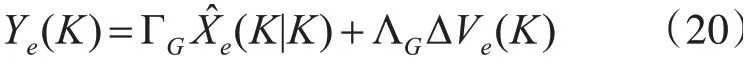
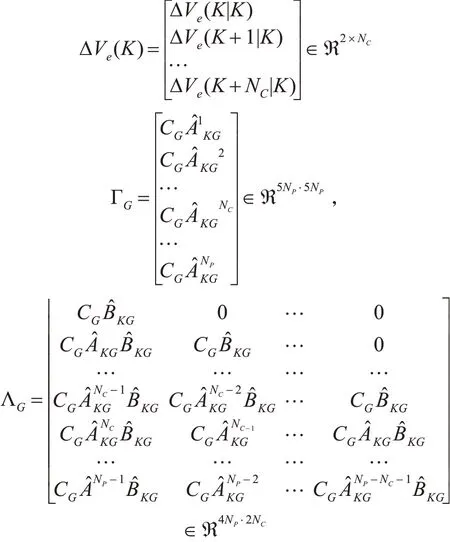
式中:
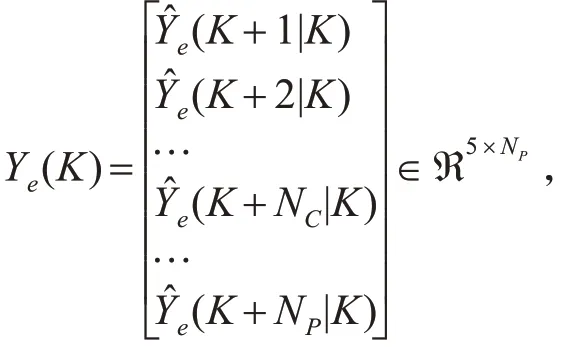
3.5 滚动优化控制输入量
MPC控制器的输出是由最小化目标函数得到的,由于在设计运动预测模型时,已将速度作为状态量并且将控制输入的偏差考虑到输入中,而输出偏差即为加速度。对无人机运动模型而言加速度就是外环输入,对无人车而言超出控制范围,所以不必再把输出偏差作为控制器的最优函数参考量,因此采用经典目标函数,设计无人车无人机的目标函数:
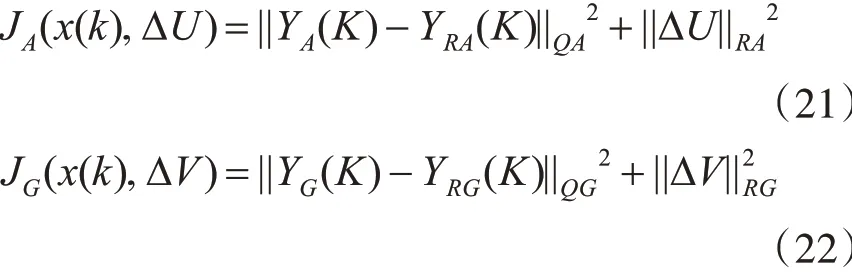
其中无人机受实际飞控姿态角角度约束,而无人车受驱动电机性能约束,可以有:
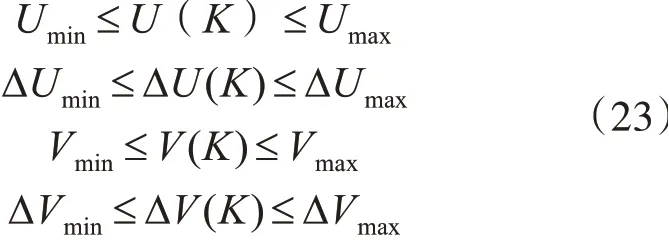
式(18)~(19)转化为二次规划问题可得:
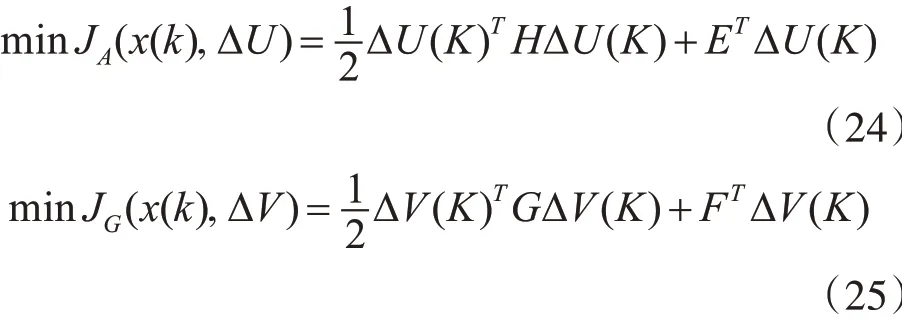
其中:
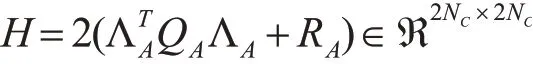
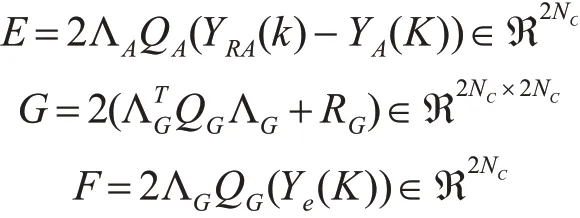
YA(K),YG(K)为无人机无人车预测输出,YRA(K)YRG(K)为无人机无人车的参考轨迹,QAQG为各自系统误差权重矩阵,RARG为各自输入权重矩阵。通过求minJA(X(K),ΔU),minJG(X(K),ΔV)的二次优化问题得到控制时域控制输入增量序列,将其中第一个控制增量作为联合运动运动中无人机无人车各自的输入。
4 仿真实验与分析
参考文献[15]无人机的姿态系统参数为m=0.5kg,l=0.3m,g=9.8m/s2,K1=0.01,K2=0.01,K3=0.01。IX=0.006kg·m2,IY=0.006kg·m2,IZ=0.012kg·m2。初始姿态角Ф=0rad,θ=0rad,Ψ=0rad。
外环控制器预测时域长度NPA为8,控制时域长度NCA为2,加权矩阵QA为diag[1 1 0.1 0.1],加权矩阵RA为diag[0.1 0.1]无状态约束,参考工程中飞控代码,将角度取0.6rad为俯仰角,横滚角的上下限,输入约束为[-6.1-8.3]≤u≤[6.1 8.3],[1.5 1.5]≤Δu≤[1.5 1.5]。无人车预测时域长度NP为20,控制时域长度NC为4,加权矩阵QG为diag[1 1 0.1 0.1],加权矩阵RG为diag[0.1 0.1]。输入约束为[-4-π]≤v≤[4 π],[-2.4-π/5]≤Δv≤[2.4 π/5]。
4.1 单无人机单无人车联合运动的仿真验证
四旋翼无人机1号初始位置为(1m,2m,4m)初始速度为(0m/s,0m/s,0m/s)。两轮差速无人车1号初始位置为(0m,0m)初始速度为(0m/s,0m/s)。
队形要求无人车紧跟虚拟领航者,无人机保持在无人车X轴后方1m的距离。仿真时间100s,仿真步长0.05s。设虚拟领航者的初始位置为(0m,0m)运动轨迹为

图4 为单无人车无人机的二维轨迹图,图5~图8为无人机无人车和参考轨迹之间的位置误差以及速度误差的关系图,由图可知位置误差保持在1m之内,虽然X方向参考轨迹是平滑的,但是无人车由于自身运动限制,不如无人机灵活,会产生波动,尤其在拐弯处波动更加明显。总体追踪精度较好。而由图9可知无人机的俯仰角θ横滚角Ф变化在0.5rad之内,满足飞控稳定性。
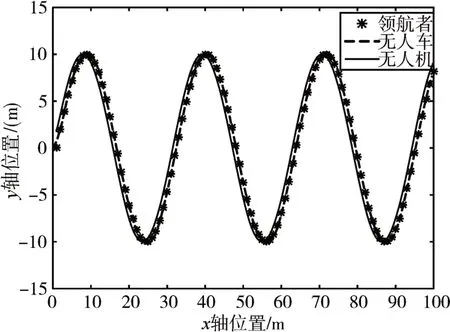
图4 单无人车单无人机联合运动控制二维轨迹图
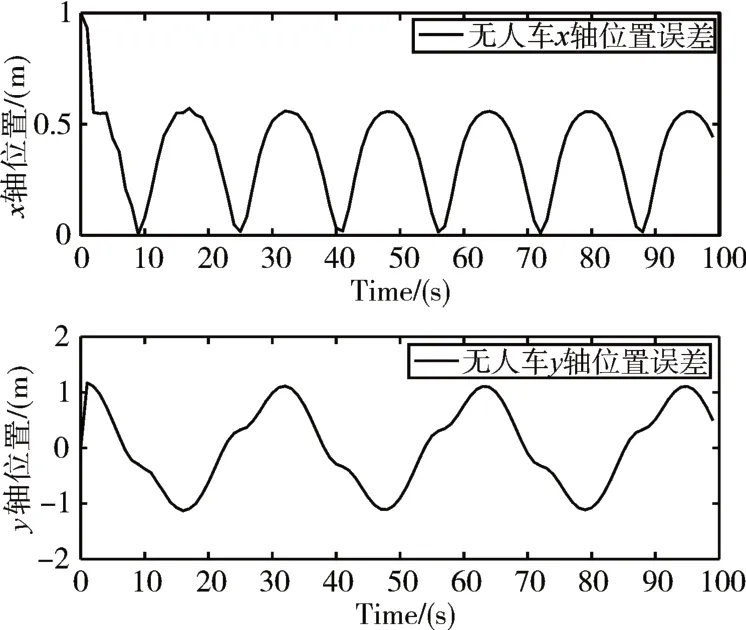
图5 无人车XY轴方向上与参考轨迹的轨迹误差
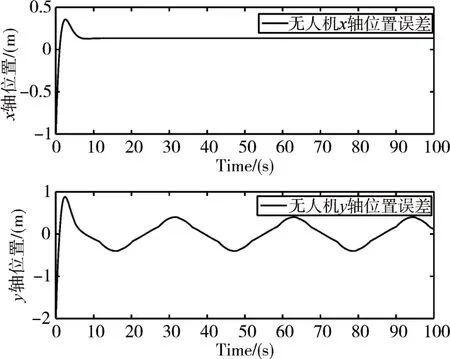
图6 无人机XY轴方向上与参考轨迹的轨迹误差
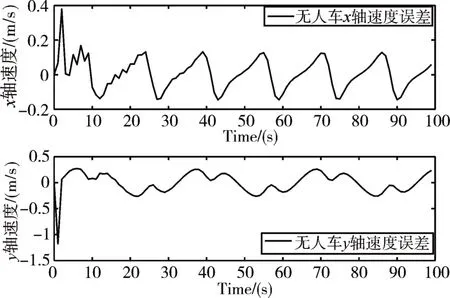
图7 无人车XY轴方向上速度误差
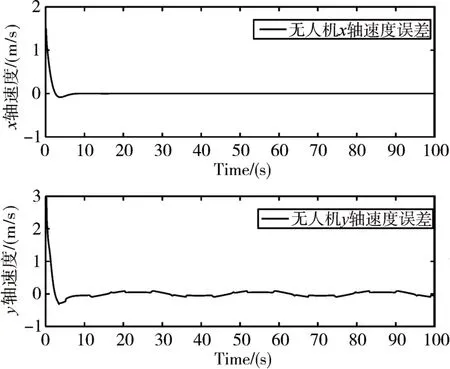
图8 无人机XY轴方向上速度误差
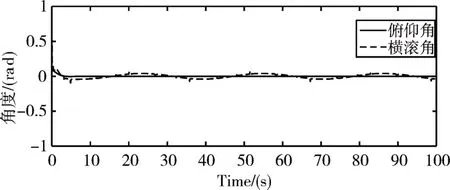
图9 无人机俯仰角横滚角的实时输出
4.2 多无人机多无人车的仿真验证
在前述实验的基础上增加无人机2号,无人车2号;之前配置保持不变。并设之前为无人机1号,无人车1号,设无人机2号初始位置为(1m,3m,4m)初始速度为(0m/s,0m/s,0m/s)设其与1号无人车保持在Y轴上方1m,同样2号无人车在1号无人车Y轴上方1m。可得无人器联合运动的二维以及三维轨迹如下。
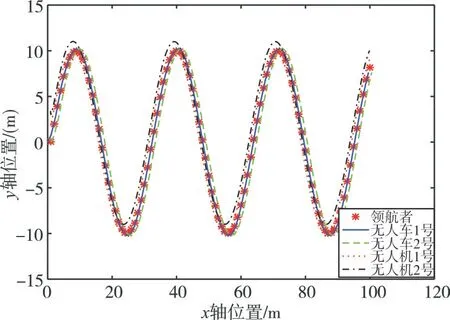
图10 多无人机无人车联合运动二维轨迹图
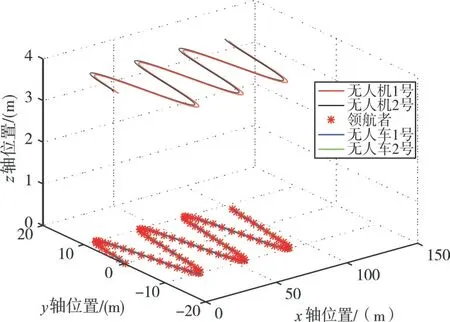
图11 多无人机无人车联合运动三维图
根据运动轨迹可知,即便在曲线运动中,在位置误差允许范围内,无人机无人车完成了较好的联合运动。
5 结语
本文将传统四旋翼无人机运动模型以及两轮差速无人车运动模型进行约束变化得到对应的MPC运动控制模型,并且将实际工程中角度约束带入预测运算,将速度约束加入轨迹约束条件提高联合编队运动性能,对无人机无人车联合运动控制实现和运行有一定工程意义,但是其中还未考虑各种阻力约束,在以后研究中将考虑加入干扰观测器提高其运动控制效果。
