巨厚松散层下开采地表下沉的影响因素分析

李青海，张存智，李开鑫，于胜文，曹有勋，杨 涛

(1.山东科技大学 能源与矿业工程学院,山东 青岛 266590；2.山东科技大学 测绘科学与工程学院，山东 青岛 266590；3.鄂托克前旗长城六号矿业有限公司，内蒙古 鄂尔多斯 017000)

0 引 言

当煤炭资源被采出后，上覆岩体所处的三向应力状态被打破，引起围岩应力重新分布，导致上覆岩层自下而上逐渐运动，依次形成垮落带、断裂带、弯曲下沉带。当弯曲下沉带扩展至地表时，将会引起地表沉陷。地表沉陷过程中有时伴随地下水位下降和水资源流失等水文地质破坏，不可避免对矿区生态环境造成影响，这与国家“绿色”发展理念相违背。推进煤炭安全绿色开采，最大限度减轻煤炭开采对生态环境的影响，实现与生态环境和谐发展是煤炭工业发展的方向。

开采区域内，上覆松散层厚度超过50 m的表土层称作厚松散层，厚度超过100 m的表土层称作巨厚松散层[1]。在松散层厚度不超过50 m的条件下，地表下沉系数(最大下沉量与煤层厚度的比值)基本为0.7～0.8[2]，而在松散层超过50 m的条件下，地表下沉系数较大，在松散层厚度超过100 m时，下沉系数接近于1.0，甚至出现大于1.0的情况[3]。专家学者对厚松散层开采覆岩运动规律进行了大量研究，其中，方新秋等[4]建立了薄基岩工作面结构力学模型；杨永康等[5]建立了综放开采的“拱—台阶”岩梁组合模型，揭示了综放的覆岩移动规律及破煤机制；鞠金峰等[6]基于特大采高工作面关键层“悬臂梁”运动对直接顶的作用，阐述了端面漏冒的发生机理；陈忠辉等[7]根据特厚煤层综放开采采高大、采空区矸石垮落不充分、不能有效支撑基本顶岩梁的特点，建立了基本顶断裂力学模型；杨治林等[8]应用初始后屈曲理论和尖点突变模型探讨了顶板岩层分岔失稳机理及屈曲后的不稳定性，建立了顶板破断后台阶下沉的判据；刘学生等[9]建立了煤层顶板破断力学模型，采用塑性极限分析定理推导了关键层的断裂步距；徐平等[10]建立了单层薄基岩Winkler弹性地基连续梁力学模型；杜锋等[11-12]建立了厚黏土层薄基岩综放采场基本顶周期来压岩层破断的力学模型。同时，基于覆岩力学特性建立了多种形式的地表沉陷预测模型，具体有SINGH等[13-14]基于弹塑性理论和现场观测数据，建立了地表沉陷预测模型。高超等[15]基于层状弹性梁板岩层沉陷控制理论和随机介质理论，建立了适合近浅埋深特厚煤层综放开采地表沉陷预测模型。杨建立等[16]基于不连续变形数值分析方法建立了地表沉陷预测模型。彭林军等[17]基于深部开采结构力学模型，提出了盆地水平煤层地表沉陷预测模型。于秋鸽等[18]将工作面上覆岩层分为关键层下部软弱岩层、关键层、松散层3部分，根据关键层理论建立了地表偏态下沉预测模型。

鉴于不同参数对地表下沉的影响较大，国内外专家学者针对不同参数对地表下沉的影响规律进行了大量研究，具体有谭志祥等[19]基于实测资料获得下沉系数与采宽比和基岩厚度的关系。张文泉等[20]模拟分析了厚松散层薄基岩条带开采中采出率、采宽、基岩厚度、松散层厚度及采高对地表下沉的影响规律。张立亚等[21]系统研究了多煤层条带开采中不同采深、不同采宽、不同层间距和上下煤柱的空间位置关系对地表下沉和水平移动的影响规律。郭振华等[22]分析了分步开挖、分步充填、膏体强度逐步增强的开采、充填过程对地表下沉的影响规律。

现有研究中对多种尺寸参数对地表下沉的影响规律进行了研究，但对厚松散层作用下不同尺寸参数比值、不同力学参数对地表下沉的影响规律研宄相对较少。因此，主要分析不同尺寸参数和不同力学参数对巨厚松散层下开采地表下沉的影响规律。在尺寸参数方面，考虑到松散层厚度、基岩厚度、煤层采高、煤层埋深等参数不同时，将会对地表下沉产生不同影响，为提高研究规律的通用性，在此选择松散层厚度与基岩厚度比，煤层埋深与煤层厚度比2个尺寸参数进行分析。在力学参数方面，在此主要考虑基岩力学参数对地表下沉的影响，选择基岩的抗拉强度、黏聚力、内摩擦角3个力学参数进行分析，以期为现场地表沉陷控制提供依据。

1 研究背景

巨野煤田内的郭屯煤矿上覆新近系和第四系黏土层平均达到590 m，属典型的巨厚松散层下开采矿井，选取该矿井1305工作面为工程背景。1305工作面煤层平均厚度4.04 m，煤层埋深约850 m，其中松散层厚约724.7 m，基岩厚约126.25 m。基岩各岩层力学参数见表1。

表1 岩层力学参数Table 1 Rock mechanics parameters

2 模型参数的确定

2.1 数值模型的建立

综合考虑模拟效果及模型运算速度等因素，采用PFC二维软件建立模型进行分析。参考1305工作面煤层赋存条件，煤层下方岩层厚度取14.71 m，煤层厚度取4.04 m，煤层上覆岩层厚度取126.25 m(受粒子数的影响，模型高度方向尺寸较小)，其中，煤层上覆岩层包含1层厚25.25 m薄基岩和1层101 m巨厚松散层，则模型高度为145 m。模型长度取500 m，建立模型如图1所示。模型中共59 708个粒子，粒子之间采用Flatjoint接触，在模型范围内施加2×104N的模拟应力梯度。模型中假设薄基岩均为泥岩，当基岩包含多层不同岩性岩层时，其对地表下沉的影响规律将在后续研究。

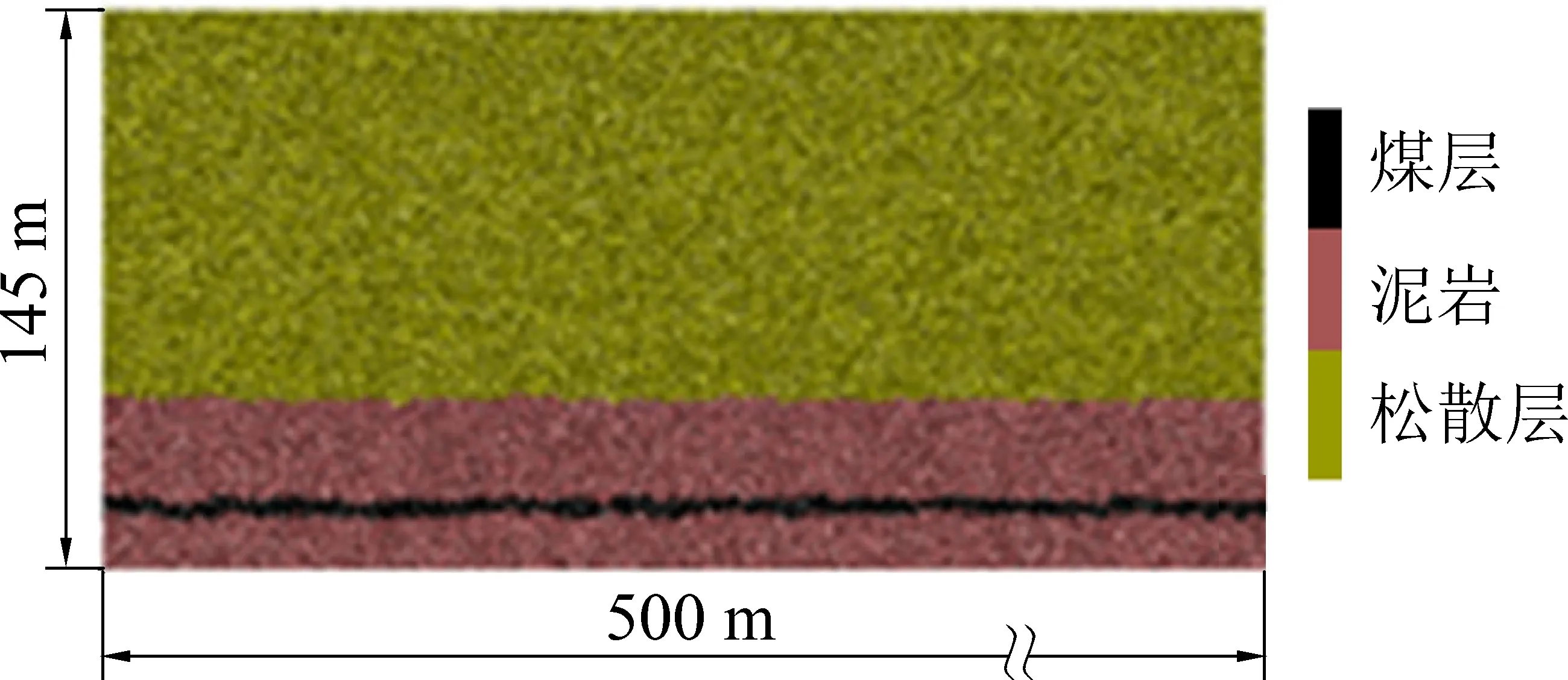
图1 1305工作面数值计算模型Fig.1 Numerical calculation model of No.1305 working face

2.2 岩体参数校核

依据参考文献[23]可知，PFC软件中输入的力学参数与数值计算获得的力学参数存在一定差异，因此，首先对岩层力学参数进行校核。在现场地质条件中由于裂隙、断层等构造的存在，现场节理岩体强度较试块强度有所弱化，而当岩体尺寸足够大、其中的块体尺寸相对较小时，岩体强度将达到稳定值。由于涉及的采场范围达到500 m，岩层高度达到145 m，其中包含的块体尺寸相对较小，因此，基于弱化后的现场节理岩体强度进行模拟分析。在此，首先基于表1提供的完整试块强度计算现场节理岩体的强度，然后通过反复调试确定数值计算中获得对应岩体强度时所需输入的相关参数。

鉴于Hoek-Brown强度准则在描述节理岩体中的优势，在此首先根据Hoek-Brown强度准则计算现场节理岩体强度数值[24]。Hoek-Brown强度准则计算公式为

(1)

其中：σ3为岩体的围压；σ1为岩体在对应围压下破坏时的应力；σc为完整试块的单轴抗压强度；mb，s，a分别为岩体参数。在节理岩体中，CAI等[25]将地质强度指标(GSI)引入具体参数计算，各参数计算公式为

(2)

(3)

(4)

式中：mi为Hoek-Brown常数；D为应力扰动因子(现场无爆破等大范围扰动时可取0)。

在岩体强度弱化的同时，岩体弹性模量弱化公式[25]为

(5)

根据现场地质资料，参考文献[24]确定细砂岩GSI取50，mi取12，泥岩GSI取40，mi取10，煤层GSI取30，mi取8。依据Hoek-Brown强度准则，获得现场各类岩体的弹性模量和不同围压下岩体强度参数见表2。

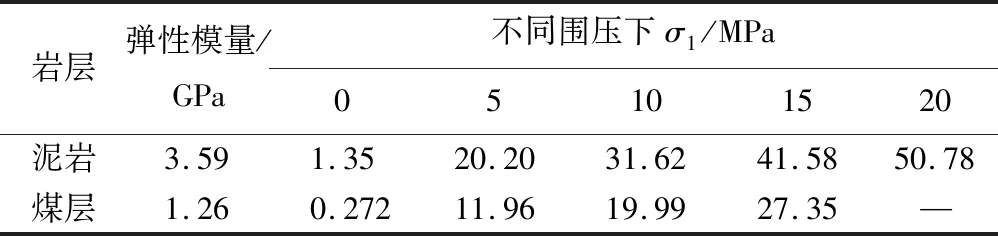
表2 现场岩体Hoek-Brown强度参数Table 2 Field rock mass Hoek-Brown strength parameters

由表2知，依据Hoek-Brown准则计算获得泥岩和煤层的单轴抗压强度分别为1.350和0.272 MPa，与现场岩体单轴抗压强度存在一定差距。基于岩层不同围压下的应力数值，拟合获得节理岩体莫尔-库伦强度准则为

泥岩：σ1=2.03σ3+10.62

煤层：σ1=1.54σ3+4.38

(6)

依据节理岩体的莫尔-库伦强度准则确定弱化后的泥岩和煤层的单轴抗压强度分别为10.28、4.34 MPa，这与现场较接近。两岩层完整试块单轴抗压强度分别为40.8、15.8 MPa，对比发现各岩体强度基本弱化为完整试块强度的0.25倍。同样基于0.25倍的弱化标准确定岩体的抗拉强度。泥岩、煤层完整试块抗拉强度分别为5.7、1.8 MPa，确定弱化后的抗拉强度分别为1.43、0.45 MPa。通过反复调试获得各岩层在数值计算中的输入参数见表3。由于松散层参数较小，依据前述的弱化准则进行弱化时发现结果离散性较大，在此，松散层参数参考土力学相关资料选取[26]，由表3可知，松散层的弹性模量、抗拉强度、黏聚力等数值均比泥岩对应参数小的多，这与现场实际相一致。基于该参数获得各岩层计算结果见表4。

表3 输入岩层力学参数Table 3 Rock mechanics parameters in simulation

表4 基于输入参数的数值计算结果Table 4 Numerical simulation results based on input parameters

2.3 开挖尺寸的确定

在数值模型中，当开挖尺寸不同时对地表下沉的影响程度不同，鉴于此，基于建立数值模型，依次计算分析在模型中间位置分别开挖120、140、160、180、200 m时地表下沉规律的差异，模拟获得120～200 m开挖尺寸模型如图2所示，地表下沉和裂隙演化与开采长度的关系如图3所示。

图2 120～200 m开挖尺寸模型Fig.2 Diagram of models excavated from 120 m to 200 m

图3 地表下沉和裂隙演化与开采长度的关系Fig.3 Relationships between surface subsidence，fracture evolution and mining lengths

由图2可知，当开挖长度分别为120、140、160、180、200 m时，模型内产生的裂隙数量分别为13 005、14 116、18 275、19 444、20 104条，地表最大下沉量分别为2.479、2.712、2.813、2.916、2.926 m。随着开挖长度的增大模型内部裂隙近于线性增加，每一次裂隙的增加表明垮落范围的进一步扩大，这与现场随着开挖长度的增加基本顶岩梁周期性断裂、工作面周期来压相一致。当开挖长度自120 m增大到180 m时，模型顶部下沉量基本呈现线性增加，而自180 m增大至200 m时最大下沉量基本无变化，则可以认为在模型走向长度为500 m时，在模型中间开挖180 m时地表最大下沉量趋于稳定，进一步增大开挖长度对最大下沉量影响不大。鉴于此，在后续分析中选择180 m开挖长度计算分析各因素对下沉系数的影响规律。

3 尺寸参数对地表下沉的影响规律分析

3.1 松散层厚度与基岩厚度比对地表下沉的影响规律

煤层埋深不变，模型高度不变，改变松散层厚度和基岩厚度，建立煤层上方松散层厚度与基岩厚度比分别为0.4、0.6、0.8、1.0、2.0、3.0、4.0、5.0、6.0、7.0、8.0、9.0、10.0的数值模型，模拟分析不同松散层厚度与基岩厚度比下沉系数演化规律。在后续分析中将松散层厚度与基岩厚度比为0.4的模型简称为0.4∶1.0模型，类似地，其他模型相应简称比为0.6∶1.0模型、0.8∶1.0模型、1∶1模型、2∶1模型等模型。模拟获得不同模型最大下沉量统计和下沉系数统计见表5。部分松散层厚度与基岩厚度比裂隙扩展规律如图4所示。定义松散层厚度与基岩厚度比为r，则r与下沉系数q的关系如图5所示，由图5可知，在r<2时，随着r的增大下沉系数迅速增大，而当r≥2时下沉系数基本趋于稳定，不再随r的增大而增大。通过拟合获得下沉系数q与r的演化关系为：

图5 下沉系数与松散层厚度/基岩厚度拟合曲线Fig.5 Fitting curve of subsidence coefficients and ratios of loose layer thickness to bedrock thickness

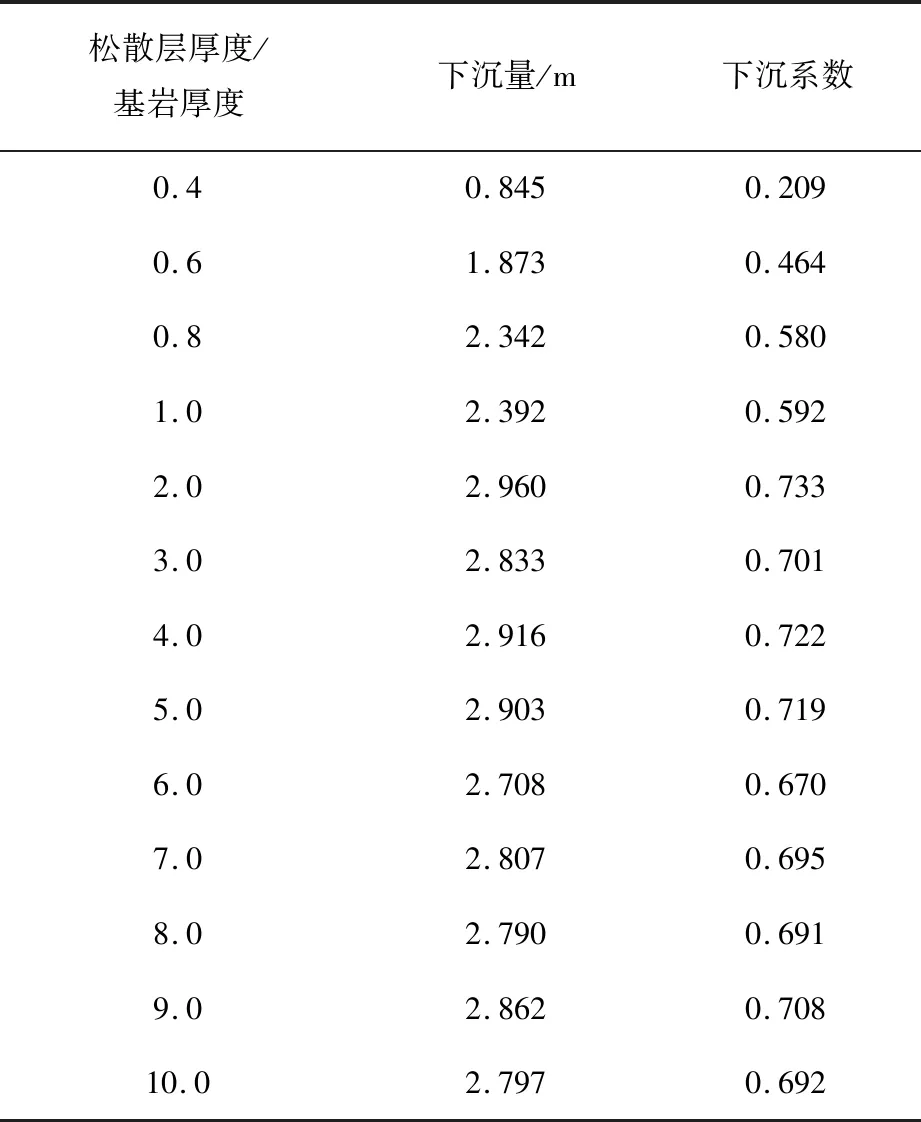
表5 不同松散层厚度/基岩厚度下沉量和下沉系数Table 5 Subsidence amounts and subsidence coefficients of models with different ratios of loose layer thickness to bedrock thickness

q=-1.719exp(-r/0.316)+0.701，R2=0.974

(7)

后续分析中选择松散层厚度与基岩厚度比为0.5、1.0、2.0、4.0，即0.5∶1模型、1∶1模型、2∶1模型、4∶1模型对比分析不同参数的影响规律。

3.2 埋深与煤厚比对地表下沉的影响规律

模型高度不变，煤层埋深126.25 m不变，煤层厚度M取2.04、2.54、3.04、4.04、5.04、6.04、7.04 m，分别建立松散层厚度与基岩厚度比为0.5∶1、1∶1、2∶1、4∶1四类模型，模拟分析不同埋深/煤厚对地表下沉的影响规律(在此假设煤层一次全部采出)。模拟获得各模型最大下沉量及下沉系数见表6。后续分析中定义埋深与煤厚比为系数P，对应获得下沉系数q和P的演化关系如图6所示。

图6 下沉系数和埋深/煤厚演化关系Fig.6 Relationships between subsidence coefficients and ratios of buried depth to coal thickness

由表4和图6可知，在不同模型中，下沉系数基本呈现随P的增大线性降低趋势，其中，4∶1模型和2∶1模型中，随P的增大下沉系数演化规律较接近且下沉系数降低速率较大，而在1∶1模型中，随P的增大下沉系数降低速率较2∶1模型减小，在0.5∶1模型中，下沉系数降低速率较1∶1模型更小，则当基岩厚度较大时(例如1∶1模型)，埋深与煤厚比对地表下沉系数的敏感性较小，而当基岩较薄时(例如4∶1模型)，埋深与煤厚比对下沉系数的敏感性较大。对比发现，当P达到61.89时，在4∶1模型、2∶1模型、1∶1模型、0.5∶1模型中地表下沉系数分别为0.347、0.353、0.398、0.321，各模型下沉系数相差不大，即当P增大到一定程度，下沉系数受松散层厚度/基岩厚度的影响较小。

4 力学参数对地表下沉的影响规律分析

4.1 基岩抗拉强度对地表下沉的影响规律

模型高度不变，煤层厚度4.04 m，煤层埋深126.25 m，煤层下方岩层厚14.71 m，建立松散层厚度与基岩厚度比分别为4∶1、2∶1、1∶1、0.5∶1.0模型，在此基础上依次改变抗拉强度数值(受计算过程影响，各模型抗拉强度数值选取并非完全相同)，统计获得不同模型最大下沉量及对应的下沉系数见表7，下沉系数与基岩抗拉强度演化关系如图7所示。

表7 不同基岩抗拉强度时下沉量和下沉系数Table 7 Subsidence amounts and subsidence coefficients of models with different tensile strengths in bedrock

图7 下沉系数与基岩抗拉强度演化关系Fig.7 Relationships between subsidence coefficients and bedrock tensile strengths

由图7可以看出，在4∶1模型、2∶1模型中，抗拉强度对下沉系数的影响规律基本一致，均呈现随抗拉强度的增大逐渐降低的趋势，同时可以看出，相同抗拉强度时两模型的下沉系数较接近。

在1∶1模型中，随着抗拉强度的变化下沉系数波动较大，整体呈现随抗拉强度的增加逐渐降低的趋势。在0.5∶1.0模型中，抗拉强度为3～7 MPa时下沉系数呈现明显的离散性，忽略该离散数值的影响，下沉系数基本呈现随抗拉强度增大逐渐降低的趋势。

4.2 基岩黏聚力对地表下沉的影响规律

模型高度不变，煤层厚度4.04 m，煤层埋深126.25 m，煤层下方岩层厚14.71 m，建立松散层厚度与基岩厚度比分别为4∶1、2∶1、1∶1、0.5∶1模型，在此基础上依次改变黏聚力(受计算过程影响，各模型黏聚力选取并非完全相同)，统计获得不同模型最大下沉量及对应下沉系数见表8。不同下沉系数对比如图8所示。可以看出，在不同模型中，下沉系数演化趋势基本一致，均是随黏聚力的增加下沉系数逐渐降低并趋于稳定。在3.05 MPa的低黏聚力状态下，4∶1模型、2∶1模型、1∶1模型、0.5∶1模型中的下沉系数分别为0.740、0.759、0.731、0.708，各模型中下沉系数均较大且数值较接近，在此黏聚力数值时下沉系数基本不随松散层厚度/基岩厚度比例的改变而改变。

表8 不同基岩黏聚力、下沉量和下沉系数Table 8 Statistical of subsidence values and subsidence coefficients with different cohesions in bedrock

图8 下沉系数与基岩黏聚力演化关系Fig.8 Relationships between subsidence coefficients and bedrock cohesion

当黏聚力自3.05 MPa提高至10.10 MPa时，0.5∶1模型中下沉系数降低幅度最大，自0.708降低至0.265，1∶1模型降低幅度次之，自0.731降低至0.367，2∶1模型降低幅度较小，自0.759降低至0.560，4∶1模型降低幅度最小，自0.740降低至0.728，则从上述分析可知，基岩厚度越厚，一定范围内提高黏聚力数值下沉系数降低越大。同时可以看出，同一岩层厚度下，随着黏聚力的增大下沉系数并非一直降低，而是存在一个临界黏聚力数值，当大于该临界值时进一步提高黏聚力时下沉系数基本无变化。对比发现，在0.5∶1、1∶1、2∶1和4∶1模型中该临界黏聚力分别是7.05、10.10、15.15和20.2 MPa，该临界值呈现随着基岩厚度降低逐渐增大的趋势。

4.3 基岩内摩擦角对地表下沉的影响规律

模型高度不变，煤层厚度4.04 m，煤层埋深126.25 m，煤层下方岩层厚度14.71 m，建立松散层厚度/基岩厚度分别为4∶1、2∶1、1∶1、0.5∶1.0模型，在此基础上依次改变内摩擦角(受计算过程影响，各模型内摩擦角选取并非完全相同)，统计获得不同模型最大下沉量及对应下沉系数见表9。不同下沉系数对比如图9所示。从图9可以看出，在不同模型中，下沉系数演化趋势基本一致，均是随内摩擦角的增加下沉系数逐渐降低并趋于稳定。当内摩擦角自5°提高至15°时，0.5∶1.0模型下沉系数降低幅度最大，下沉系数自0.495降至0.252，降幅达到0.243，1∶1模型、2∶1模型和4∶1模型降低幅度基本相同，1∶1模型中下沉系数自0.592降至0.463，降幅为0.129，2∶1模型和4∶1模型中下沉系数基本自0.722降至0.601，降幅为0.121。

图9 下沉系数与基岩内摩擦角演化关系Fig.9 Relationships between subsidence coefficients and bedrock internal friction angles

表9 不同基岩内摩擦角、下沉量和下沉系数Table 9 Subsidence values and subsidence coefficients of models with different internal friction angles in bedrock

同时可以看出，基岩厚度一定时存在一个临界内摩擦角，在小于临界值范围内改变内摩擦角值下沉系数变化较大，而当大于该临界值时进一步提高内摩擦角值下沉系数基本无变化。对比发现，在0.5∶1模型中该临界内摩擦角约是12.5°，在1∶1、2∶1和4∶1模型中该临界内摩擦角约是20°。同时，虽然1∶1、2∶1和4∶1模型临界内摩擦角数值一致，但是由于各模型基岩厚度的差异，在达到临界内摩擦角时，对应的下沉系数差异明显，1∶1模型下沉系数最小，其值为0.393，2∶1模型次之，其值为0.50，4∶1模型最大，其值为0.582。达到临界内摩擦角后，地表下沉系数基本呈现基岩厚度越大，下沉系数越小，基岩厚度越小，下沉系数越大的反比关系。

5 结 论

1)下沉系数基本呈现当松散层厚度与基岩厚度比r<2时，随着r的增大下沉系数迅速增大，而当r≥2时下沉系数基本趋于稳定，不再随r的增大而增大。

2)下沉系数基本随着埋深与煤厚比P的增大呈现线性降低趋势。当基岩厚度较大时(例如1∶1模型)，地表下沉系数对埋深与煤厚比的敏感性较低，当基岩较薄时(例如4∶1模型)，地表下沉系数对埋深与煤比厚的敏感性较高。

3)下沉系数基本呈现随着抗拉强度的增大逐渐降低的趋势。基岩厚度一定时，存在临界黏聚力，在小于临界值的范围内提高黏聚力下沉系数逐渐降低，当超过该临界值时进一步提高黏聚力下沉系数基本无变化；同样地，存在临界内摩擦角，在小于临界值的范围内提高内摩擦角下沉系数逐渐降低，而当大于该临界值时进一步提高内摩擦角值下沉系数基本无变化。