实时电价下含换电站的孤立微电网双层优化调度
2021-11-30郭兴众杨秀茹
王 昊,郭兴众,杨秀茹
(安徽工程大学 高端装备先进感知与智能控制教育部重点实验室,安徽 芜湖 241000)
面对全球能源不断紧张的局面,电动汽车产业已经成为热门产业。我国近些年加大了对电动汽车产业的投入,电动汽车可以充当负荷吸收微电网中多余的能量,将电动汽车入网技术运用于微电网,可以实现微电网盈利。
伴随电动汽车进入人们的生活,电动汽车电池换电站作为电动汽车能源供给的主要来源应运而生。将换电站与含可再生能源的微电网结合,对有效利用可再生能源具有重大作用,使得换电站和微电网各自的收益最大。文献[5-6]分别在充电和换电两种不同的模式下计算含电动汽车的微电网经济调度模型,证明了在相同条件下,换电模式比充电模式更能提高微电网的经济性。文献[7]在含分布式电源的微电网模型基础上,加入电动汽车换电站模型,论证了换电站的储能作用。文献[8]以网损最小为目标函数,利用遗传算法对含有光伏发电的充电站集中调度,通过充电站最优充放电计划的安排降低负荷峰谷差和网损。文献[9]提出了微电网和电动汽车换电站的模型,利用入侵杂草算法优化,同时对比其他优化算法突出此算法的优越性。文献[10]建立不同目标函数,以换电站充电功率为变量参与有序充电调度。
目前对微电网的研究多集中于微电网的经济调度优化问题。文献[11]从负荷需求侧出发,综合考虑微源出力、需求侧管理、环境治理三种成本为目标函数,运用改进粒子群算法优化,最后解决了孤立微电网供电不足的问题。文献[12]考虑了可再生能源出力不稳定性对孤立微电网的影响,将基础负荷功率电源和调频电源作为调频特性的部分,实施两步优化,先日前调度确定基础电源的出力,再制定调频电源的出力方案。但是,此调度未能发挥基础电源出力的灵活性,降低了微电网的调节能力。
研究将传统储能系统接入微电网的模式代替为电动汽车电池交换站的接入。以风电机组、光伏机组、电动汽车电池交换站及柴油发电机组作为孤立微电网的内部结构模型,以孤立微电网成本最小和换电站利益最大分别建立双层模型,以不平衡功率引导的电价和换电站充放电总功率作为双层模型联系的桥梁,并以此网为例验证模型的有效性。
1 孤立微电网结构和双层调度
研究基于换电站的孤立微电网模型。微电网内部由风机、光伏、柴油发电机、电池换电站及负荷组成。其中,风、光是自然资源,不同时刻的出力具有不确定性,输出功率不可控;柴油发电机属于可控制的分布式电源,可以由微电网控制其出力。而换电站与微电网不是同一个经济实体,所以两者之间的调度须通过微电网制定的电价引导换电站的出力,进而将换电站的出力计划反馈给微电网,微电网得到反馈优化柴油机的出力,调整电价。
含换电站的孤立微电网调度如图1所示。由图1可知,上层模型通过制定内部电价优化下层换电站充、放电功率,下层将功率反馈给上层微电网,从而实现两者的利益最大化。其中,电价是自变量,换电站的出力功率是因变量。

图1 含换电站的孤立微电网调度
2 基于双层优化的孤立微电网模型
2.1 上层孤立微电网模型
上层模型是通过优化柴油发电机不同时刻的出力以及制定电价使其净成本最小。
(1)风机(WT)数学模型。
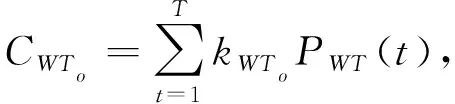
(1)
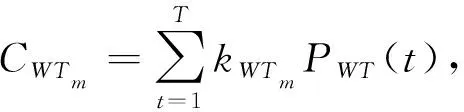
(2)
C
=C
+C
,(3)
式中,C
表示WT运行时需要的管理成本;C
表示WT管理电源产生的费用;k
表示WT单位运行的维护系数;k
表示WT发电管理费用系数;P
(t
)为第t
时段WT出力;T
为调度周期。(2)光伏发电(PV)模型。
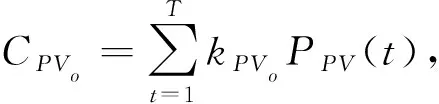
(4)

(5)
C
=C
+C
,(6)
式中,C
表示PV运行时需要的管理成本;C
表示PV管理电源产生的成本费用;k
表示PV单位运行时的维护系数;k
表示PV的发电管理费用系数;P
(t
)为第t
时段PV出力;T
为调度周期。(3)柴油发电模型。设定微电网处于孤岛运行情景下,故除分布式电源供电以外的微电网剩余负荷均由柴油发电机组承担。柴油发电机在运行的过程中会产生运行费、燃料费和气体污染处理费用。
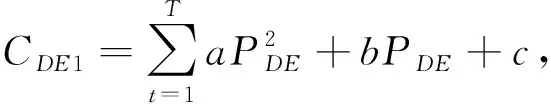
(7)

(8)

(9)
C
=C
1+C
2+C
3,(10)
式中,C
1为柴油机消耗燃料的成本;C
2为柴油机的运行成本;C
3为柴油机对气体污染物的处理成本;P
为柴油发电机的实际功率;a
、b
、c
分别为柴油发电机的系数;k
是柴油机的运行维护系数;C
是对i
类气体污染物处理的成本系数;α
是柴油机运行时产生i
类气体污染物的排放量。(4)可中断负荷模型。孤立微电网主要用于偏远的地方,远离大电网,利用内部微源独立发电作用于负荷。当微源出力不足以提供负荷供电需求时,则需要考虑中断负荷的供应,由电网控制负荷的工作状态,对被中断负荷的用户给予补偿。

(11)
式中,C
为孤立微电网出力不足而导致的中断负荷补偿成本;k
表示中断负荷的单位补偿费用;P
(t
)为t
时刻中断负荷的功率。(5)弃风、弃光成本模型。在负荷水平不高的情况下,微电网中会存在多余的微源出力,造成可再生能源的浪费,主要存在多余风、光能源的不及时消纳。其成本模型如下:
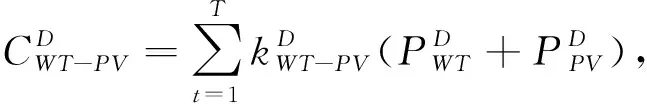
(12)
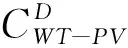
(6)能量交换成本。换电站在低负荷的阶段吸收多余的微电网功率,在高负荷阶段释放自身存储的功率,起到削峰填谷的作用,所以换电站与微电网之间存在能量交换,成本模型如下:

(13)
式中,C
为能量交换成本;e
为t
时刻的电价;P
(t
)为微电网和换电站在t
时刻的交换功率,换电站向微电网购电时P
(t
)为正,反之为负。综上,孤立微电网的成本模型如下:

(14)
上层目标函数的约束条件如下:
①功率平衡约束
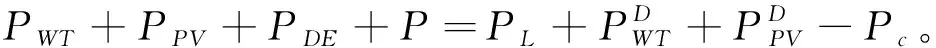
(15)
②柴油发电机功率约束
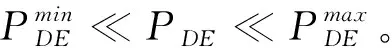
(16)
2.2 下层电动汽车换电站的模型
电动汽车换电站可以更换电动汽车的电池,并对换下的电池进行充放电并存储。本模型以整个换电站的储能为控制目标,对其参与微电网的充、放电过程进行控制。在任意t
时刻,换电站内有一部分电机处于充电状态,也有一部分电机处于放电状态,所以在t
时刻换电站总的充放电功率为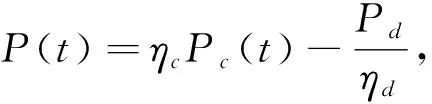
(17)
式中,P
(t
)、P
分别是电机在t
时刻的总充、放电功率;η
、η
分别是充、放电效率。换电站根据上层的电价调整自身的充放电功率,从而实现换电站利益最大化,即
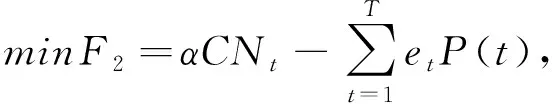
(18)
式中,α
为换电站向电动汽车用户提供的换电零售价;N
是电动汽车用户向换电站更换电池的需求量;C
为电池的额定容量。下层目标函数的约束条件如下:
(1)任何时刻换电站电池电量应该满足用户的换电需求
CN
≤q
≤q
,(19)
式中,q
是换电站t
时刻存储的电池电量;q
是换电站最大存储电量。(2)电量平衡
q
=q
-1+P
-1Δt
-CN
-1。(20)
(3)换电站内电机的数量有限,所以总充放电功率具有约束。在t
时刻,换电站最大的充、放电功率为
(21)
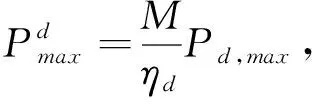
(22)

(23)
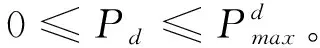
(24)
2.3 实时电价的制定
为了优化换电站充放电功率,孤立微电网采用实时动态电价模式。分时电价具有改善用户充电习惯,对微电网内部起到削峰填谷,降低微电网和用户费用成本的作用,是时间段的电价。研究的电价是根据每一个时刻的负荷变化来制定每一时刻的相应电价,是时间点的电价。
实时动态电价是基于不平衡功率来制定的。当微电网孤立运行时,电网中不平衡功率为
P
=P
+P
+P
-P
,(25)
为了制定实时动态电价,引入不平衡率U
,计算如式(26)所示:
(26)
根据以上U
的值,U
在各个取值范围的电价如表1所示。
表1 波动范围和电价的制定
3 基于改进遗传算法的双层模型优化
研究基于改进遗传算法求解双层优化模型。为提高最优解和优化效率,研究对传统遗传算法加以改进。对于实数问题的优化,设置一个步长为step
的邻域扰动算子,将个体的染色体任意一个位置进行一点或多点扰动,即随机生成-1至1之间的随机数rand
,然后在染色体原位置上的值加上step
*rand
。引入步长step
,整体扰动策略分为两个部分,将全局扰动策略运用于总进化次数的前一半,即将每个染色体的基因位都进行扰动;同理,将局部扰动策略运用于总进化次数的剩余过程,即从个体的染色体中任意选择一个基因位进行扰动,且扰动的步长为step
=step
*(1-rate
),(27)

(28)
式中,rate
是迭代次数;i
是当前迭代次数;maxgen
是最大迭代次数,即步长随着进化代数的增加而降低。扰动变量r
作如下改进:low
=-step
,(29)
up
=step
,(30)
(1)rate
<0.
5,r
=r
*(up
-low
)+low
。(31)
(2)rate
>0.
5,存在扰动概率m
,当rand
<m
,r
=rand
*(up
-low
)+low
,(32)
式中,low
、up
分别是扰动下界和扰动上界;rand
是0~1的随机数。最后,把扰动变量的值赋予个体,得到新个体进入下次优化。采用整体策略的好处在于,不仅使算法前期收敛速度快,而且后期算法的局部搜索能力也大为提高。运用此种改进遗传算法解决研究双层模型的具体求解流程如图2所示。
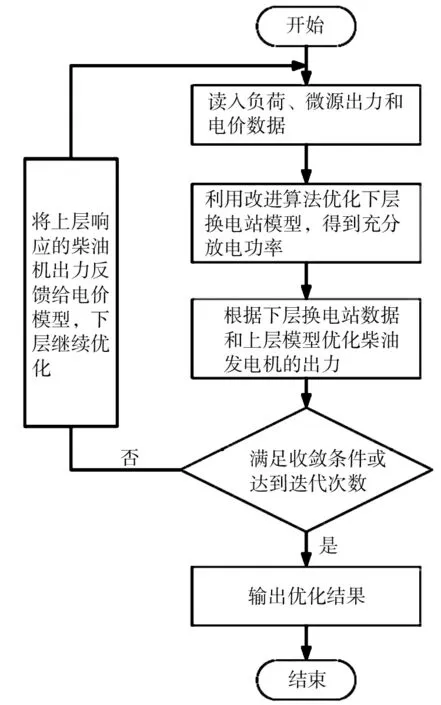
图2 改进遗传算法求解模型
4 算例分析
4.1 参数设置
孤立微电网系统由风电机组、光伏机组、电动汽车电池交换站及柴油发电机组成。微电网内部基础参数如下:柴油发电机的出力限制范围为0~100 kW,系数a、b、c分别为0.000 11、0.180 1、6。调度周期为1 d,设定1 h为一个研究时段。微电网中基础负荷功率数据和风光发电出力的预测数据分别如图3、图4所示。各微源的成本系数,柴油发电机的污染物排放量和治理费用,以及微电网弃风弃光和切负荷的单位补偿成本系数分别如表2、表3、表4所示。

表2 各个微源的成本系数

表3 污染物治理费用和排放系数

表4 弃风弃光和切负荷单位补偿成本

图3 负荷功率曲线图4 风光出力预测曲线
换电站的参数如下:假定换电站有50台充放电机,充放电功率均为8 kW,充放电效率均为0.95;站内每个电动汽车的电池容量均为30 kWh,型号均相同。换电零售价取统一价格为1.3 元/(kW·h)。电动汽车各时段的换电需求以及微电网一天的分时电价如图5、表5所示。
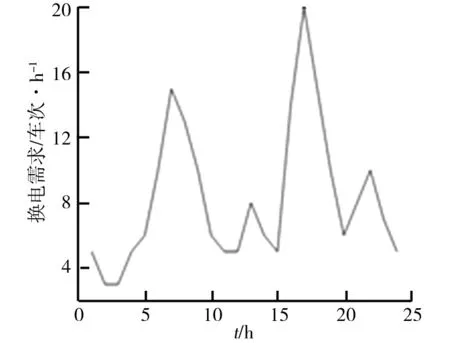
图5 用户换电需求

表5 分时电价数据
改进遗传算法参数为:种群规模为100,交叉概率、变异概率分别为0.6、0.01,最大迭代次数为1 000。步长因子越大,加快收敛,结果容易在最优值附近震荡;而因子越小,收敛减慢,但容易找到最优值。综上,步长因子为0.001。
4.2 结果分析
为了说明孤立微电网与电动汽车换电站互动带来的经济效益,研究设计了两种方案进行仿真对比:方案1是基于分时电价下孤立微电网与电动汽车换电站的互动;方案2是基于实时电价下孤立微电网与电动汽车换电站的互动。
方案1及方案2的换电站总充放电功率曲线图如图6、图7所示。上述两类图中换电站都满足在低电价阶段大规模充电,在高电价阶段适当放电,以此增加换电站收益。但图7在采用实时电价后,换电站总充放电功率随每时刻电价的变化而变化,且变化范围大、频率高、追踪效果好。所以方案2下换电站收益更好。

图6 方案1中换电站总充放电功率图7 方案2中换电站总充放电功率
两种方案下微电网总成本和换电站总利润如表6所示。方案1和方案2中微电网的总成本如图8、图9所示。方案1和方案2中换电站的总利润如图10、图11所示。由表6可以看出,在微电网总成本方面,方案1的总成本为4 938.96元,而方案2的总成本为3 374.81元。对比方案1,方案2的微电网总成本减少了1 564.15元,即31.7%;在两者换电站收益方面,方案1、方案2的换电站收益分别为625.21和3 641.47元,相比方案1可以看出,方案2收益增加明显,为482%。上述分析表明,实时电价的实行有利于最大化微电网和换电站的经济利益。

表6 两种方案中微电网成本和换电站利润

图8 方案1中微电网总成本图9 方案2中微电网总成本
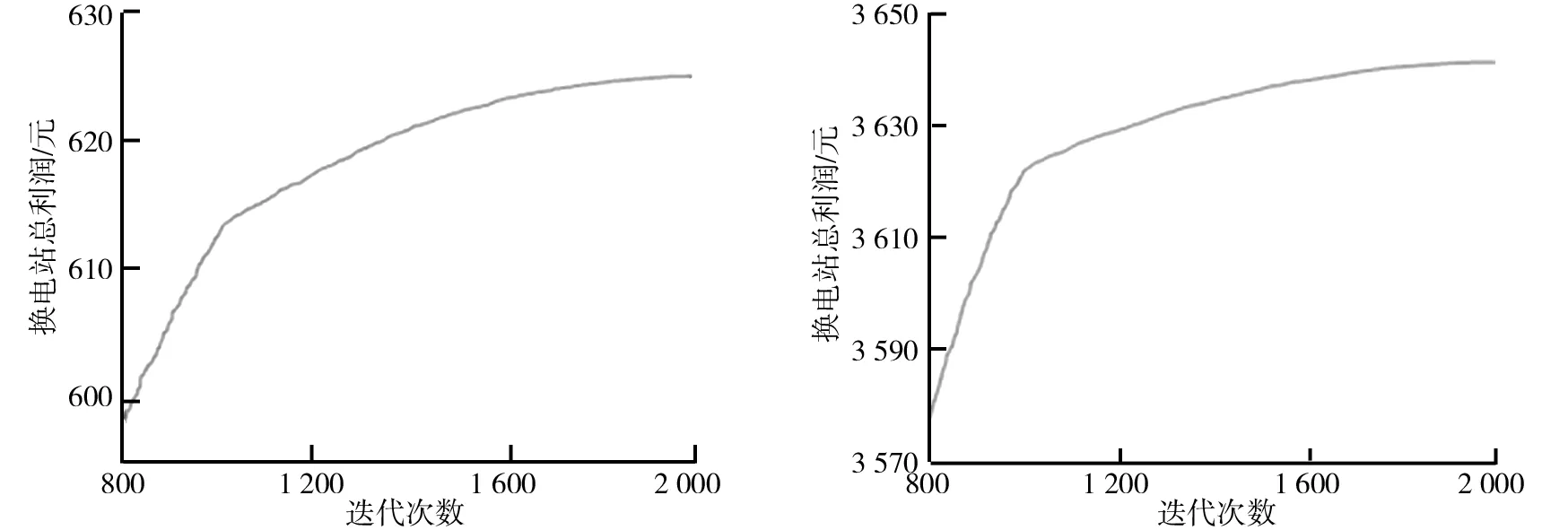
图10 方案1中换电站总利润图11 方案2中换电站总利润
模拟退火算法学习的是金属退火的原理,是由开始给定的温度慢慢冷却的过程。由于该算法有一定的概率跳出局部最优解,能以较快速度找到问题的近似最优解,但并不一定能找到全局最优解,同时,结果也受到温度的初始值和退火速度等影响。为了比较改进遗传算法的优越性,研究用模拟退火算法对微电网和换电站的双层模型进行优化,对比两种算法的结果。模拟退火算法下在实时电价方案中微电网的总成本和换电站的总利润如图12、图13所示。对比图12、图13,在微电网总成本方面,改进遗传算法的最优值好于模拟退火算法,其拥有更好的全局搜索最优解的能力。在换电站利润方面,模拟退火算法收敛速度过快,导致得不到全局最优解。

图12 模拟退火算法下微电网总成本图13 模拟退火算法下换电站总利润
5 结论
研究利用改进遗传算法对孤立微电网和电动汽车电池换电站两种不同的利益主体的双层模型进行优化。仿真结果表明,研究提出的基于孤立微电网和电动汽车电池换电站的双层模型及算法不仅可以降低微电网成本,而且可以最大化换电站的利益。同时,与模拟退火算法相比,改进遗传算法精度更高。
