基于有限缓冲区的混流装配线排产优化

徐 兵，杨新愉

(长春工业大学机电工程学院，长春 130012)

0 引言

随着生产需求多样且复杂化，混流装配的生产方式越来越多的被企业应用，混流装配线的投产排序问题也越来越被企业和学者关注。文献[1]首次提出混流装配线的平衡和排序问题，后期利用单一产品装配线的相关技术和方法最早解决了混流装配线的平衡问题。文献[2]设计了基于禁忌搜索的遗传算法对混流装配线平衡和排序的优化问题进行求解。

由于空间资源的限制，研究缓冲区有限的混流装配线排产优化问题虽更复杂却也更具备实际意义。文献[3-4]提出了改进ICA算法，求解具有有限缓冲区的柔性流水车间排产优化问题研究。文献[5]提出一种混合探路者算法对带能耗阈值约束和有限缓冲区的绿色流水车间调度问题进行了求解。粒子群算法因其概念简明、实现方便、收敛速度快等优点，近年来越来越多的被运用于解决此类NP-hard[6]等组合优化问题中。文献[7]为了解决柔性流水车间有限缓冲区间歇调度问题，提出了一种自适应细胞自动变异粒子群优化算法，表明了该算法具有很强的鲁棒性，寻优结果较优。文献[8]为了解决多车间混流装配线的作业排序问题，提出了种群库概念改进离散粒子群算法。

对排产优化问题，许多学者做了很多努力但是大多数研究往往针对一条生产线解决单一LBFFSP问题，无法针对企业缓冲区有限和多生产线等多因素的实际情况解决排产优化问题。因此，基于前人对粒子群算法在组合优化问题上的研究，本文结合部分企业生产线的实际情况，引用了基于惯性权重的粒子群算法，研究混流装配线的排产优化和缓冲区容量限制问题。

1 混流装配线排产数学模型

1.1 问题描述

氮氧化物传感器的生产具有多品种小批量的特点，其生产工艺流程主要分为三大工序：底座与外壳的生产、半成品装配、成品检验。本文研究的主要是前两道工艺的排产优化问题，其数学规划模型如图1所示。

图1 具有有限缓冲区的混流装配线排产数学规划模型

此类传感器的生产由两条子生产线和总装配线复合而成，即子生产线是由一条专门生产不同种类的底座和一条生产不同类型外壳的混流生产线所组成。缓冲区的大小影响着整条线的生产效率，为了提高氮氧化物传感器的生产效率及实现子生产线与总装配线的生产负荷均衡。特此，在总装配线的前一道工序设立一个有限缓冲区。该生产线根据当天生产计划进行排产需考虑以下要素：

①第一条子生产线加工的第一个工件如果与第二条子生产线第一个加工的工件同时完成，则该两条子线加工出来的半成品不需要相互等待可直接进入下一道装配线进行组装；

②若两条子线的第一个工件不是同时加工完毕，则先出来的工件需要等待后出来的工件然后再进入装配线进行组装；

③投产顺序在第二及以后的工件在完成各自子生产线最后一道工序的加工后，需考虑工件出来的先后顺序、缓冲区的容量、缓冲区内工件的数量以及装配线上第一道工序是否空闲等因素；才能决定当前工件是否堵塞在现在的工位上、是否进入缓冲区等待、是否进入装配线上进行下一步的加工。

在排产过程中经常会存在两条子线生产加工出来的产品因速度不一样导致需要组装的产品相互等待、装配线装配的时间过长而缓冲区的容量不够导致前面子线出现堵塞现象甚至停机停产，因此研究子生产线和装配线的投产顺序以及缓冲区容量的大小对缩短产品的生产周期和提高设备的利用率有着至关重要的作用。针对这种生产模式，本文优化了子生产线和装配线的投产顺序以及有限缓冲区的容量。为方便讨论，文中对于子生产线和装配线及缓冲区所组成的生产系统统称为混流装配线。

1.2 数学模型

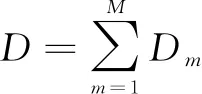
1.3 符号定义

该生产线基本符合Fm|blocking|Cmax阻塞流水车间调度问题[9]的描述，每一条子生产线及装配线上的工件i及机器j都是独立的，π={π(1),π(2),...,π(n)}表示一个工件序列，其中n=ds；为方便讨论，引入以下符号：

①第一条子生产线：pπ(i),j表示工件i在机器j上的加工时间；b表示这条线最后一台机器后面的缓冲区的工位数；dπ(i),j表示工件i在机器j上完成加工后的释放时间；第一条子生产线dπ(i),j的计算过程如下：

dπ(1),1=pπ(1),1,i=1,j=1;

(1)

dπ(1),j=dπ(1),j-1+pπ(1),j,i=1;j=2,3,…,m;

(2)

dπ(i),1=max{dπ(i-1),1+pπ(i),1,dπ(i-1),j+1},i=2,3,…,n;j=1;

(3)

dπ(i),j=max{dπ(i),j-1+pπ(i),j,dπ(i-1),j+1},i=2,3,…,n;j=2,3,…m-1;

(4)

dπ(i),j=max{dπ(i-1),j,dπ(i),j-1}+pπ(i),j,i≤b+1;j=m;

(5)

dπ(i),j=max{max{dπ(i-1),j,dπ(i),j-1}+pπ(i),j,ZDπ(i-1),1},i>b+1;j=m;

(6)

②第二条子生产线：Pπ(i),j表示工件i在机器j上的加工时间；π={π(1),π(2),...,π(n)}表示一个工件序列；B表示这条线最后一台机器后所设立的缓冲区的工位数；Dπ(i),j表示工件i在机器j上完成加工后的释放时间；第二条子生产线的Dπ(i),j计算与上述计算完全一致，下列列举总装配线需要用到的部分公式，计算过程如下：

Dπ(1),1=Pπ(1),1,i=1;j=1;

(7)

Dπ(i),j=max{Dπ(i-1),j,Dπ(i),j-1}+Pπ(i),j,i≤B+1;j=m;

(8)

Dπ(i),j=max{max{Dπ(j-1),j,Dπ(i),j-1}+Pπ(i),j,ZDπ(i-1),1},i>B+1;j=m;

(9)

③总装配线：ZPi,j表示工件i在机器j上的装配时间；π={π(1),π(2),...,π(n)}表示一个工件序列；ZDπ(i),j表示工件i在机器j上完成加工后的释放时间；Cmax(π)表示一个工件序列π的总加工时间，所有可能的加工序列集合用Π表示。ZDπ(i),j与Cmax(π)的计算过程如下：

ZDπ(1),1=max{dπ(1),m,Dπ(1),m}+ZPπ(1),1,i=1;j=1;

(10)

ZDπ(i),1=max{max{dπ(i),m,Dπ(i),m,ZDπ(i-1),1}+ZPπ(i),1,ZDπ(i-1),j+1},i=2,3…n;

(11)

ZDπ(1),j=ZDπ(1),j-1+ZPπ(1),j,i=1;j=2,3,…m;

(12)

ZDπ(i),j=max{max{ZDπ(i-1),j,ZDπ(i),j-1}+ZPπ(i),ZDπ(i-1),j+1},i=2,3,…,n;j=2,3,…,m-1;

(13)

ZDπ(i),j=max{ZDπ(i-1),j,ZDπ(i),j-1}+ZPπ(i),j,i=2,3,…,n;j=m;

(14)

Cmax(π)=ZDπ(n),m

(15)

1.4 目标函数

求解有限缓冲区的混流装配线排产优化问题，就是寻找一个加工序列π*，使得该序列所有工件经过子生产线及总装配线的加工，完成的总加工时间最小，即满足Π。

Cmax(π*)≤Cmax(π),∀π∈∏

(16)

寻找最佳的缓冲区容量，就是找到最小的缓冲区B*、b*，使得该容量下缓冲区所起的作用接近无限缓冲区，以尽量减少缓冲区工位数占用生产线的空间资源。根据式(1)～式(15)，当缓冲区B,b趋于无穷的时候，存在一个工件序列使得总加工时间最少，即满足N。

(17)

2 问题的求解方法

子生产线与装配线是两个不同的工艺阶段，为了保证满足产品型号及数量符合订单需求，根据后面瓶颈工序装配线的投产顺序决定前两条子生产线的零部件的投产次序。在有限缓冲区按照先进先出不改变投产顺序的规则下，它们既相关又独立，因此，按照两个不同的工艺阶段，先研究装配线的装配排序，再研究子生产线的投产顺序。

对于混流装配线的排序问题，许多学者运用粒子群算法(PSO)求解这类问题均取得了较好的效果[10]。然而因为粒子群算法有易于陷入局部最优的缺点，文章采用线性递减惯性权重[11-12]的粒子群算法求解本文研究的具有有限缓冲区的混流装配线排产优化问题，通过将惯性权重w设置为动态变化引入PSO算法中，提高算法后期的局部搜索能力，使得算法跳出局部最优从而找到最好的解。根据本文研究混流装配线的特点，最大生产周期随着有限缓冲区的容量变化而变化，具有有限缓冲区的混流装配线排产优化问题的粒子群算法流程设置如图2所示。

图2 粒子群算法求解混流装配线流程图

2.1 粒子群算法设计

(1)编码解码。粒子群算法中的每个粒子都代表一种生产排序方式，粒子的维度表示加工序列总的工件数，该算法的编码方式运用粒子的每个维度代表一个工件。采用rands函数，其在[-1,1]随机产生的任意实数表示粒子每一维的位置，把随机生成的实数按照从小到大的规则排序，以排序后的位置顺序为基准与维数进行映射，从而获得工件的加工顺序。设某一加工序列工件数为6，即粒子的维度为6，表1详细介绍了粒子的编码解码方法。

表1 粒子编码解码方法

(2)初始种群。随机产生的实数经一定规则重新排序后得到新的工件序列为初始种群。

(3)适应度值计算。根据式(1)～式(15)编写适应度函数并运用MATLAB软件进行计算。

(4)引入惯性权重w。为了避免算法陷入局部最优，在粒子群更新速度和位置的初期，引入线性递减的惯性权重w，随着迭代的进行，惯性权重动态变化，迭代初期较大的惯性权重使得算法保持了较强的全局搜索能力，而迭代后期较小的惯性权重利于算法进行更精确的局部搜索。通过五种惯性权重的算法性能比较，采用公式(18)引用惯性系数。

w(k)=wstart-(wstart-wend)(k/Tmax)2

(18)

其中，Wstart为初始惯性权重；Wend为迭代到最后一代时的惯性权重；k为当前迭代代数；Tmax为最大迭代代数。

(5)粒子速度与位置更新。在每次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，其公式参考文献[13]即：

(19)

(20)

(6)局部优化。为了提高粒子群算法的局部搜索能力，对每代速度位置更新后生成的粒子进行局部变异，随机生成两个[-1,1]的随机数更新粒子位置，形成领域解,通过sort函数将领域解转换成工件排序，通过设置循环次数不断搜索更新领域最优解。通过局部搜索，可以提高粒子个体新解的质量。

2.2 最大生产周期算法设计

清楚了解每条生产线零部件出来的时间先后顺序及装配线第一道工序的运行情况和缓冲区是否满负荷，就会方便计算工件序列在整个生产系统的最大生产周期。本文针对混流生产系统，设计了有限缓冲区容量由B=0,b=0时最大生产周期不断向无限缓冲区时最大生产周期靠近而逐步增加的计算算法，流程如图2所示。以下介绍了工件在各个阶段是否释放的计算算法，用于判断每个工件在任意时间点所在机器的闲忙状态。设计了工件在各个生产阶段是否释放的计算算法，方法如下：

步骤1：参数初始化。0时刻的工件开始加工时间为0，缓冲区工件数量为0。

步骤2：对两条子生产线SL(1,2)每一次加工完成进入缓冲区的时间以及后一条装配线第一道工序机器闲忙状态进行判断。

(1)对第一个工件在第一条生产线完成最后一道工序的释放时间dπ(1),m和第二条生产线的第一个工件完成最后一道工序的释放时间Dπ(1),m进行比较；此时，装配线上的第一道工序机器空闲，工件在两条子生产线最后一道工序SL(1,2),m上正常释放，取释放时间长的作为后一道工序的开始加工时间ZSπ(1),1=max{dπ(1),m,Dπ(1),m}。

(2)令i=i+1，i∈(1,2,…,n-1)。在x时刻作出判断，第一步先判断第一条生产线第i个工件完成最后一道工序SL1,j=m的释放时间dπ(i),m与第二条生产线第i个工件完成最后一道工序SL2,j=m的释放时间Dπ(i),m，再判断缓冲区内是否有工件、缓冲区工件数是否已达到最大容量、第i-{B,b}-1个工件在装配线上的第一道工序ZL3,j=1是否释放；若缓冲区内无剩余容量且第i-{B,b}-1个工件在ZL3,j=1上正在加工，此时该机器在忙，第i个工件被堵塞在当前工位上；若缓冲区内有剩余容量，则无论ZL3,j=1是否空闲，工件i在加工完成后正常释放。

(3)返回步骤(2)，并开始循环判断，直到i=n-1，即判断完一个序列π的最后一个工件的生产状态后跳出循环。

步骤3：计算得出最后结果。

3 案例分析

设某日公司内的一条混流装配线生产7种氮氧化合物传感器，传统排产方式规定一班次为一个最小循环，假设在一个班次对7种产品的需求量分别为D(1),D(2),...,D(7),7种产品经过组装线的3道工序进行组装，组装时间如表2所示。

表2 各种产品在装配线上各工序的加工时间

某日该线氮氧化物传感器的日生产任务为生产A1、B1、C1、D1、E1、F1、G1等7种不同品种传感器共150件，7种产品在一个最小循环数量分别为5:7:7:5:8:8:10，一个班次为50件产品，分三次完成。表3为一个最小循环生产这7种氮氧化物传感器所需要的零部件类型及数量，表4是各零部件在各自生产线上各工序的加工时间。

表3 各种产品所需零部件数量

表4 各工序加工时间

运用粒子群算法寻找个体最优值，整个生产系统参数设置如下：迭代次数为200，粒子种群规模为20，粒子的维数为50，学习因子c1=c2=1.49，最终得到两条子生产线及装配线的最佳投产排序为：3 21 6 32 36 17 11 18 19 10 28 37 2 46 38 44 30 22 14 5 35 49 31 20 12 48 25 34 4 33 1 43 50 29 40 41 26 24 9 15 16 7 42 23 8 13 47 45 27 39，通过粒子编码解码得到该传感器最佳排序为：ADBEFCBCCBEFAGFGEDCAFGEDBGEFAFAGGEFGEDBCCBGDBCGGEF；最短生产周期为448 min，与传统排产方式所得的生产周期480 min，缩短了生产周期6.7%；第一、二条子生产线最佳的缓冲区容量分别是B为17、b为14，因此总的缓冲区最小可设为31便能达到无限缓冲区的效果。最小生产周期迭代如图3所示。

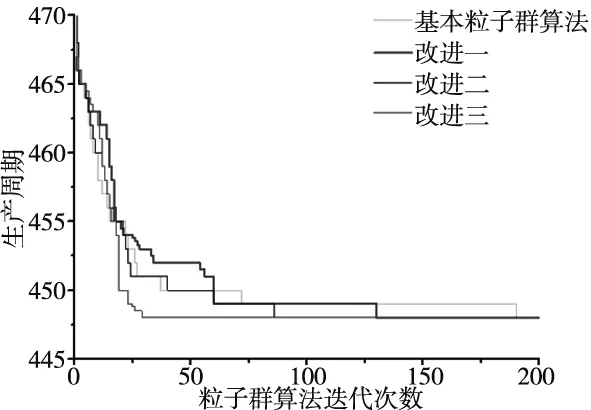
图3 粒子群算法改进图

由图3可知，基本粒子群算法及改进后的粒子群算法能快速找到比传统排序更优的生产排序，通过引用惯性权重及遗传变异不断改进后的粒子群算法，其寻优能力及收敛速度比改进前有了显著提高，验证了改进后算法的有效性。

4 总结

混流装配线的投产排序问题在企业多品种少批量的生产模式下起着重要的作用。本文以某公司一氮氧化物传感器生产线为例，研究了具有有限缓冲区的两条子生产线及装配线复合而成的生产系统排序问题。针对不同零件在机器设备加工时间不均衡的约束，分别对子线及总装线的运行匹配度进行优化，以减少零件在机器上的堵塞时间。采用基本粒子群算法对每一排序进行生产周期的计算，引用惯性权重提高算法的全局搜索能力，并采用随机变异方式改进算法，提高粒子的多样性，最终得到该生产任务的最优排序方案以及缓冲区的最佳容量，显著提高了企业该生产线的生产效率及资源利用率。