塔架式钢结构吸热塔的优化设计研究
2021-11-29陈俊岭张劲尧章荣国
陈俊岭,张劲尧,章荣国,邹 辉
(1.同济大学建筑工程系,上海 200092;2.上海电力设计院有限公司,上海 200025)
0 前 言
太阳能是一种取之不尽的清洁能源,发展潜力巨大。近年来,在国家政策的支持下,中国太阳能发电市场保持高速发展[1]。吸热塔是光热发电中太阳能收集的核心部分,具有高度大、顶部重量大、温度影响敏感等特点。目前,国内外对吸热塔结构的优化研究比较少,但与之类似的高耸结构在优化设计方面的研究成果非常丰富。Guedez[2]等以塞维利亚地区的塔式光热发电厂为研究背景,提出了一种基于热经济学的塔式太阳能光热电站的优化设计方法,该方法可确定成本、获利能力和投资之间的最佳折衷曲线。崔磊和邓洪洲[3]运用相对差商算法,对输电塔的塔腿辅材进行了优化,结果表明该方法的优化效果优于遗传算法和模拟退化算法。徐奴文等[4]运用遗传算法,在简化荷载作用下,以屈曲性能为约束,对风力机塔架进行了最优化设计,得到了较满意的结果。孟冉和马宏旺[5]采用遗传算法对预应力钢筋混凝土风机塔进行了优化,运用Python语言编译了遗传算法ABAQUS命令流文件,实现了遗传算法与ABAQUS的对接,为解决大型复杂结构的优化问题提供了一种新思路。罗乐[6]采用遗传算法,对特高压输电塔进行了截面优化、形状优化和拓扑优化,该算法能够自动寻找最优截面面积、节点位置、塔身节点个数、辅材及横撑的数量,显著地减小了用钢量。陈俊岭等[7]提出一种组合式塔架用于大型风电机组,综合考虑应力、频率和长细比约束等因素,基于粒子群算法对下部格构式塔架进行形状和杆件截面优化。
目前已建成的吸热塔结构大多采用单筒形式的钢筋混凝土结构,一方面是因为单筒形式的钢筋混凝土塔筒形式简单、施工方便;另一方面是因为吸热塔的顶部有质量巨大的熔盐吸热器,一般认为钢筋混凝土结构具有较高的刚度和承载能力。实际上,格构式钢塔架是传统高耸结构常用的结构形式,具有刚度大、加工安装方便、材料用量省等优点,但在吸热塔结构中的应用尚比较少。本文以某100 MW熔盐塔式光热电站的200 m高吸热塔为工程背景,通过采用有限元分析软件ABAQUS对连续体进行拓扑优化得到格构式塔架杆件布置的大体形式,再运用基于遗传算法的Matlab优化设计程序对各项设计参数进行优化,为太阳能热发电站钢结构吸热塔的优化设计提供参考。
1 ABAQUS拓扑优化
根据传统高耸结构的设计经验,格构式塔架底部宽度一般取塔高的1/4~1/10[8]。初选格构式塔架的底部宽度为塔高的1/8,塔架高度为200 m,塔架底部宽度确定为25 m;塔架顶部宽度根据顶部吸热器的尺寸确定为15 m。根据上述参数确定格构式塔架的基结构,建立单元类型为S4R的棱柱体壳单元模型作为拓扑优化的设计域。
根据吸热塔的受力特点,待优化模型承受的荷载主要包括顶部吸热器的重力荷载、吸热器上作用的风荷载、井道以及塔体上作用的风荷载。格构式塔架的井道一般布置在塔体中心,常常设计为自承重结构:即井道结构的重量由井道本身承担并直接传递至基础,井道上的风荷载通过横杆和横隔传递至外塔架主体,由格构式塔架承担。本文采用实体模型进行拓扑优化时,由于井道在塔体的内部,仅按实体模型的轮廓面积沿高度分为16段计算塔架上作用的风荷载,作用在吸热器上的风荷载等效为塔架顶部的水平集中力。塔架底部设置为完全固定支座,考虑风荷载作用方向的不确定性,增加了对称约束条件,强制棱柱壳体的4个面具有相同的结构,初始模型如图1。

图1 待优化模型的边界条件示意图
通过拓扑优化,得到如图2所示优化结果,结构中可以不布置材料的部分已经被删去,只留下对结构刚度贡献较大的部位。从图2可以看出,塔柱布置在棱边,腹杆的布置方式为交叉形。整体看来优化结果合理,力的传递路线明显,但塔面上的腹杆只有斜杆,没有横杆,可能的原因是在拓扑优化中塔体的受力以水平力为主,而实际中横杆的受力通常很小,塔架的抗侧刚度主要由斜杆贡献,因此在拓扑优化中只保留了斜杆部位的材料。传统高耸结构中的格构式塔架体系一般由塔柱、斜腹杆、横杆等主要杆件组成,不同杆件在体系中所起的作用不同。一般而言,塔架在水平荷载下产生的倾覆弯矩由受压(拉)的塔柱共同承担;水平荷载在塔体内产生的剪力由斜腹杆受拉或受压承担;横杆的受力较小,但其具有非常重要的作用,不仅可以减小塔柱和斜杆的计算长度,和横隔协同作用可确保多边形塔架横截面的几何不变性,增加塔架的抗侧刚度。总体而言,结构拓扑优化只是一种概念性设计,它可以为设计人员提供结构优化的参考方案,在实际设计中还需要根据实际经验和具体情况,对拓扑优化的结果做出进一步改进[9]。

图2 拓扑优化结果示意图
格构式塔架腹杆常见的布置方式有单斜杆、交叉斜杆、“米”字形腹杆、再分式腹杆、K式腹杆等多种形式。本文的格构式吸热塔架高度为200 m,拓扑优化后塔柱和斜杆的长度为20~30 m,因此最终决定在斜杆交叉点增设横杆形成 “米”字型腹杆,同时配置图3所示的横隔来减小塔柱和斜杆的长细比。需要注意的是,吸热塔顶部放置吸热器等设备,设计时横隔的布置应结合井道结构进行布置,但本文由于缺少井道结构的相关设计资料,且考虑到横隔在塔架中的主要作用是维持塔架横截面的几何不变性[10],因此为了便于编写优化设计程序,横隔的结构布置进行了如图3所示的简化处理。

图3 钢塔架横隔布置示意图
2 遗传算法优化程序
2.1 遗传算法
遗传算法是一种随机搜索的优化算法,其基本思想来源于达尔文的进化论和孟德尔的遗传学说,通过模拟自然界的生物进化过程来求解问题[11]。进化过程主要通过选择、交叉、变异来实现,具体运算步骤如下:
(1) 设置初始参数,如染色体长度、种群数量、交叉概率、变异概率等。
(2) 随机地生成初始群体。
(3) 评价个体的适应性:通过预设规则,计算种群中各个体的适应度。
(4) 选择运算:按照适应度越大选择概率越大的原则,选择新群体。
(5) 交叉运算:两两交叉,生成新群体。
(6) 变异运算:染色体基因随机地发生变异。
(7) 判断终止条件:若最优个体满足约束条件,且迭代次数达到预设值,则输出最优解,终止程序;否则跳转至步骤(3)。
2.2 数学模型
(1) 目标函数
本文以吸热塔结构总质量为目标函数,通过将杆件的质量乘以1.2的放大系数来考虑节点质量,见式(1)。
(1)
式中:W为结构总质量,kg;Lj为第j号杆件的长度,m;ρj为第j号杆件的材料密度,kg/m3;Aj为第j号杆件的横截面积,m2。
(2) 约束条件
根据GB 50135-2019《高耸结构设计标准》[12]第5.2.1条规定,塔桅钢结构宜按整体空间桁架做静力结构分析。因此格构式塔架中的所有构件都可视作轴心受力构件,优化过程中的约束条件主要包括强度、整体稳定性、位移、长细比的限值要求。
1) 应力约束条件
拉应力约束条件
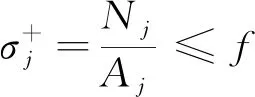
(2)
受压稳定约束条件

(3)
以上的两种应力状态可以在数学上简化为“等效应力”[6],等效应力约束条件为:
(4)
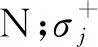
2) 位移约束
根据GB 50135-2019《高耸结构设计标准》[12]第3.0.11条的规定,高耸结构在以风为主的荷载标准组合下,钢塔架按线性分析的水平位移角限值不得大于1/75。因此,结构优化的位移约束条件为:
umax=u*
(5)
式中:umax为最大水平位移,m;u*为水平位移限值,m,为塔架高度的1/75。
3) 杆件长细比约束
(6)
式中:λj为第j号杆件的长细比;λc为压杆的容许长细比,λt为拉杆的容许长细比,按GB 50135-2019《高耸结构设计标准》第5.5.4条采用。
(3) 罚函数
钢塔架的优化设计属于离散变量的优化问题,每条染色体都代表一种可能解,但这种解并不一定能够满足上述的约束条件,如果直接采用结构总质量作为适应度函数,会导致优化结果中出现大量结构总质量很低但是不满足约束条件的个体。为了考虑约束条件,可以采用罚函数的方法来建立适应度函数。通过罚函数形式定义的目标函数如式(7)所示:
(7)
(8)
(9)
(10)
式中:Cv为目标函数,kg-1;d1,d2,d3分别按式(8)~(10)计算,代表位移、应力、长细比与规范限值的相对差值;σmax为最大等效应力值,MPa;λmax为最大长细比,λ*为相应的长细比限值;penal表示罚函数的惩罚因子,是一个很大的常数。当所选个体满足约束条件时,由于惩罚因子的放大作用,其适应度值将远远小于满足约束条件的个体,从而将不满足约束条件的个体过滤掉。
3 截面优化和形状优化
3.1 截面优化
(1) 优化参数的选取
为使得截面优化结果贴近设计经验、满足设计要求,本文通过设置截面库的方式,将所有杆件沿高度方向分层、根据杆件位置分类。所有杆件均采用圆钢管,沿高度方向分为10层,每层的塔柱、斜杆、横杆和横隔采用不同规格截面,共有40种规格的圆钢管。根据设计经验,格构式塔架中的横杆虽然受力较小,但是当腹杆为“米”字型时,为便于构件之间的连接,一般情况下交叉点处的横杆保持连续、斜杆断开,因此横杆截面应不小于斜杆截面,因此将斜杆与横杆截面用同一变量来表示,则设计变量个数为30。根据型钢规格表及常用的径厚比,共设计了128种钢管截面作为截面库,以7位数的二进制编码表示,则染色体的总长度为210位,每一条染色体就表示一种截面的设计方案。优化参数如表1所示。限于篇幅,截面库的规格不再单独列出。

表1 截面优化参数设置表
(2) 优化结果及分析
经过67次的迭代后,结构的总重量即收敛得到一个较好的优化结果,结构重量的进化曲线如图4所示。由图4可以看出,结构重量随着迭代次数的增加逐步下降并趋于稳定。
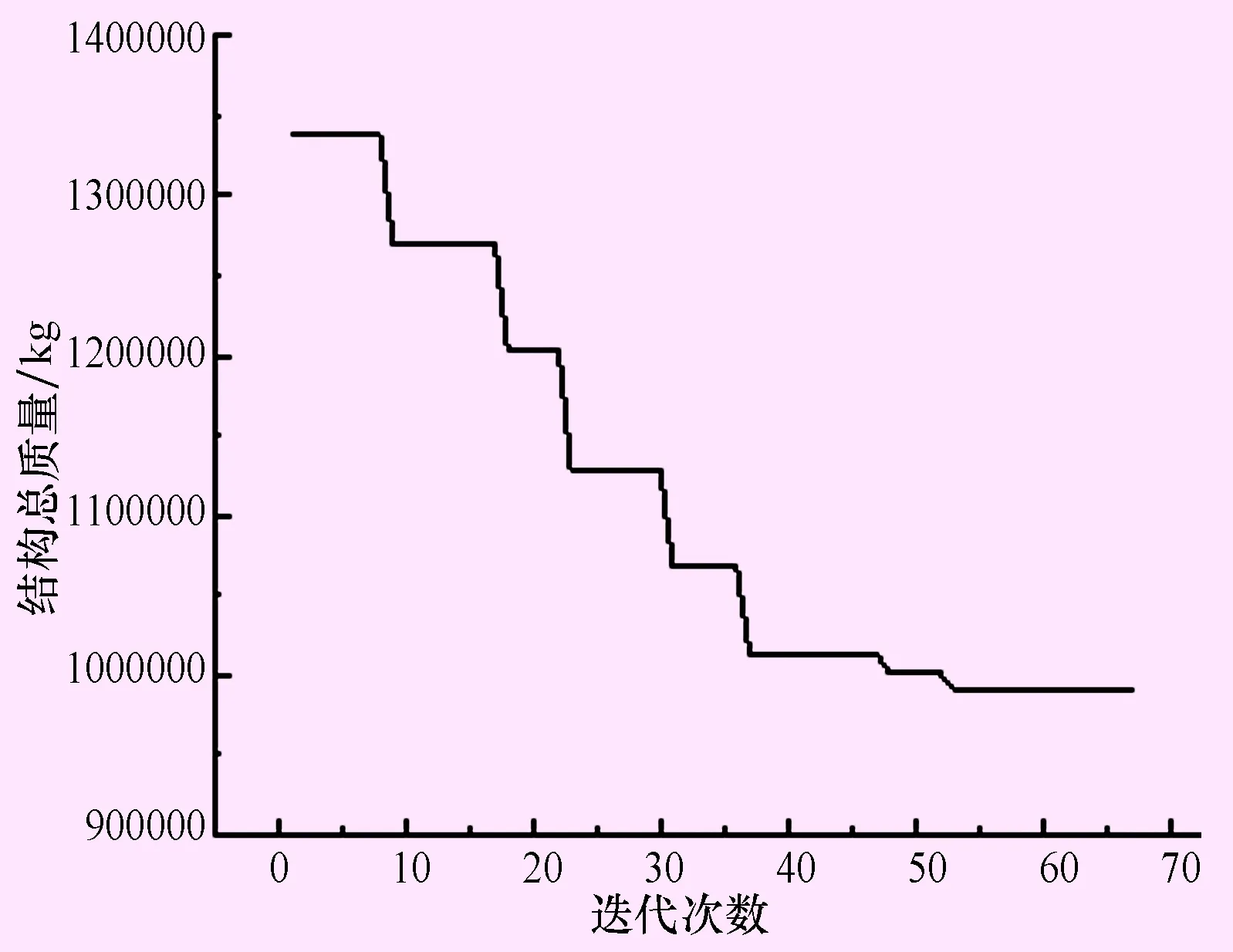
图4 结构总质量随迭代次数的变化曲线图
10次随机运行的截面优化结果见表2,结果中最大质量为998 574 kg,最小质量为990 706 kg,相差0.7%,可见本文程序具有比较好的收敛性。

表2 钢结构吸热塔的截面优化结果表
塔架中的最大应力出现在底层塔柱部位,图5为最大等效应力值的变化曲线。最大等效应力值起初为315 MPa,超过了强度设计值295 MPa,随着迭代次数的增加,由于罚函数的作用将不满足强度条件的个体淘汰,等效应力最大值总体呈上升趋势,最终收敛于271 MPa。
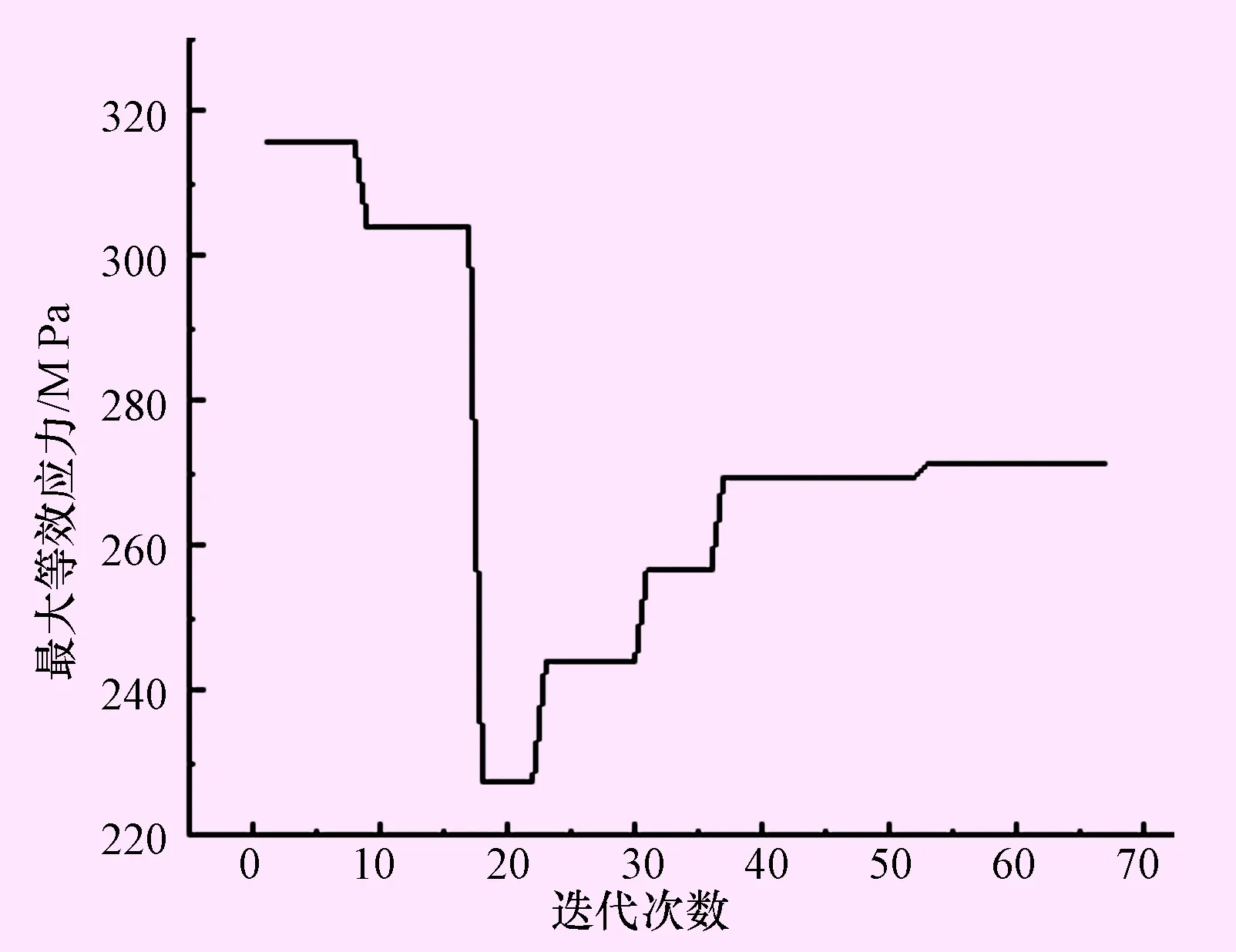
图5 最大等效应力值随迭代次数的变化曲线图
3.2 形状优化
(1) 优化参数的选取
增加各层塔架结点的竖向坐标改变量为新的设计变量,调节各节段的高度。将塔柱外轮廓线分段,调整每个折线段的倾斜角度,实现塔架各节段宽度的优化。分别将塔架的外轮廓线分为2、3、4、5段,对比不同分段情况下的优化结果。以3段式为例,形状优化的参数设置见表3。

表3 形状优化参数设置表
(2) 优化结果及分析
1) 折线分段数参数化分析结果
分别将外轮廓线分为2、3、4、5段,每种分段情况下进行10次形状优化,结果见图6。

图6 不同折线型分段数的优化结果图
从图6中可以观察到,优化后结构总质量的最小值发生在分段数为5的情况,但是收敛性较差。分段数为3时,优化后的结构总质量较低,且收敛性较好。因此本文将塔架的折线分段数取为3。
2) 结构重量变化
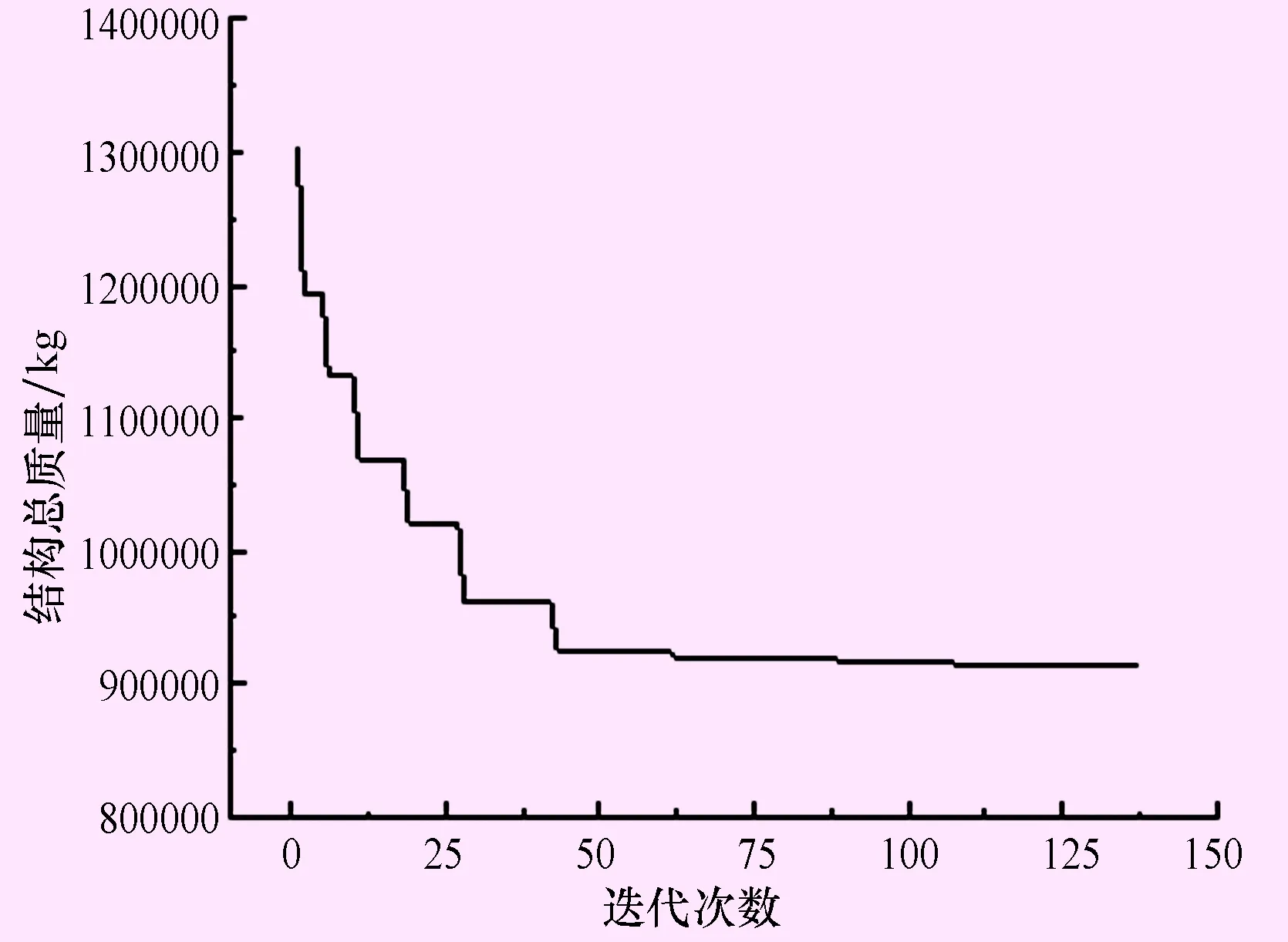
图7 结构重量随迭代次数的变化曲线图
结构的重量变化趋势见图7。结构总质量随着迭代次数的增加逐步下降并趋于稳定,经过137次迭代后收敛于912 804 kg。该最小值相比较于截面优化的结果降低了7.9%。
3) 截面尺寸、形状参数的优化结果尺寸、形状优化的结果见表4、5。
优化后的塔架的立面示意图如图8所示。

表4 优化后塔架构件的截面参数表

表5 优化后的形状参数列表
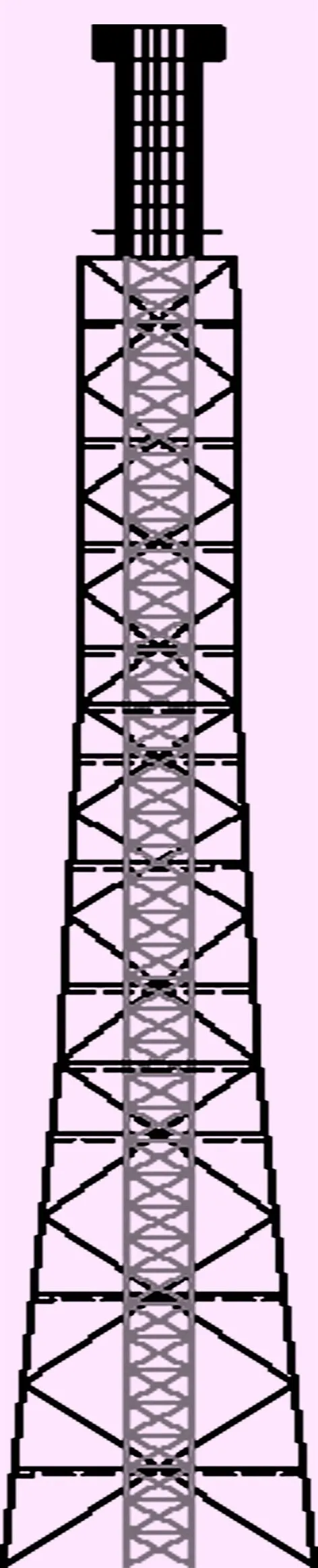
图8 优化后吸热塔的立面示意图
4 结 论
本文通过ABAQUS的拓扑优化模块,在设计域内实现了拓扑优化,得到了塔架的初始构型。通过基于遗传算法的Matlab程序实现了钢结构吸热塔的截面优化和形状优化,可以得出以下结论:
(1) 在ABAQUS中建立锥台型的壳单元模型,基于变密度法原理,可以很好地实现基本模型的拓扑优化,得到塔架腹杆初始布局形式,优化结果基本符合钢塔架的设计习惯,为后续的截面尺寸优化和形状优化提供了基结构。
(2) 通过遗传算法,以杆件截面面积作为优化设计变量,可以在拓扑优化得到基结构的基础上实现截面尺寸优化,得到合理的杆件截面布局,截面的材料利用更加充分,同时能够实现结构总质量最小化,降低总造价。
(3) 通过结点的移动和外轮廓线角度的变化,可以实现钢塔架的形状优化。经过截面尺寸和形状的组合优化后,结构的总重量进一步降低,优化效果相对于单纯的截面尺寸优化更好。同时塔架各节段的高度、宽度和立面廓线型式更加合理,外形更加美观。
