公路隧道洞口浅埋段围岩压力计算方法探讨
2021-11-29韩文斌
韩文斌,薛 旋
(中国电建集团西北勘测设计研究院有限公司,西安 710065)
0 前 言
公路山岭隧道从生态、环保角度考虑,严格遵循“早进洞、晚出洞”原则,甚至洞口出现“零”开挖现象。为此,隧道进、出口需穿越较长浅埋段,该地段围岩一般以Ⅳ~Ⅵ级为主,地质条件较差,开挖过程中易出现围岩掉块、坍塌,支护结构开裂、变形等现象。一直以来,公路隧道洞口被视为隧道实施的重难点、高风险区域。为避免此类现象的发生,降低工程风险,设计前期需根据地质及周边情况,选择合理的计算方法,分析得到围岩压力,进行支护与结构设计,确保浅埋段洞口的安全、经济、可靠。常规浅埋段围岩压力按松散体考虑,且至地表,采用荷载-结构法计算时,在一定围岩厚度范围内围岩压力偏大,经验支护参数无法满足设计要求。若采用地层-结构法计算时,围岩压力明显较小,支护结构参数符合常规经验值。本文结合设计经验与规范理论,对洞口浅埋段围岩压力计算方法进行论述,提出较合理的计算方法,为公路隧道洞口浅埋段围岩压力计算提供思路。
1 规范计算方法及存在的问题
1.1 规范计算方法
根据JTG 3370.1-2018《公路隧道设计规范》(第一册 土建工程)[1]附录D规定(以下简称规范),浅埋段隧道围岩压力计算方法如下:
(1) 超浅埋段:埋深H小于或等于等效荷载高度hq时,垂直压力视为均布:
q浅1=γ·H
(1)
式中:q浅1为垂直均布压力,kN/m2;γ为隧道上覆围岩重度,kN/m3;H为隧道埋深,指隧道至顶面的距离,m。
侧向压力e按均布荷载考虑时,其值为:
(2)
式中:e浅1为侧向均布压力,kN/m2;Ht为隧道高度,m;φc为围岩计算摩擦角,°。
(2) 浅埋段:埋深H大于hq,小于Hp(Ⅳ~Ⅵ级围岩取Hp=2.5hq)时,围岩垂直压力均布荷载:
(3)
式中:q浅2为垂直均布压力,kN/m2Bt为隧道开挖宽度,m;θ为洞顶开挖宽度范围下沉岩体与两侧沿面的摩擦角,°,Ⅳ级围岩取0.7~0.9φc,Ⅴ级围岩取0.5~0.7φc。
λ为侧压力系数。
(4)
(5)
式中:β为破裂面与水平面夹角,°。
侧压力视为均布压力时:
(6)
1.2 存在的问题
从上述公式(1)~(6)看出,隧道洞口浅埋段围岩压力按塌落拱等效荷载高度hq为界,分2种情况考虑围岩坍塌、滑移产生的松散压力。当洞顶埋深H小于或等于等效荷载高度hq时,洞顶至地面深度内围岩均考虑沿两侧破裂滑移斜面(破裂角为 )整体滑移、坍塌对结构产生围岩压力;当埋深H大于hq,小于2.5hq时,洞顶至地面深度内围岩考虑在开挖宽度范围内松散围岩先下沉,对两侧岩面产生较大下滑力,从而带动两侧岩体沿一定的斜面滑移,最终对结构产生围岩压力,浅埋隧道荷载分布示意见图1。
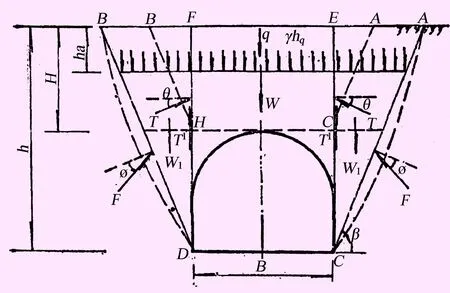
图1 浅埋隧道荷载分布示意图
从已实施的山岭隧道来看,上述理论计算公式与实际差别较大,主要存在以下问题:
(1) 一般洞口以Ⅳ~Ⅵ级围岩为主,按照规范规定,洞口段浅、深埋分界深度为2.5hq。以双车道开挖宽度9 m≤Bt<14 m为例,算得:hq=5~38.3 m,2.5hq=12.5~34.25 m,假定洞口天然地形坡比为1∶1,隧道浅埋段长度与埋深相当,浅埋段整体较短,若按上述公式分段计算围岩压力,需对应2种不同的支护与衬砌结构,在两断面分界处存在扩挖的现象,且支护与衬砌纵向整体性差,不利于围岩与结构稳定,施工繁琐。
(2) 对于公式(3)~(6)算得的围岩压力较大,相对应的支护与衬砌结构设计参数值(支护与衬砌厚度等)远大于规范建议值与经验值,导致理论与实际不符。
2 计算方法探讨
公路隧道浅埋段围岩压力计算方法来源于TB 10003-2016《铁路隧道设计规范》,它以大量的铁路坍方调查资料为依据,通过统计回归分析,提出了围岩压力计算公式。李鹏飞[2]等人对7种围岩压力计算公式:普氏公式、太沙基公式、全土柱理论[3]、比尔鲍曼公式以及《公路隧道设计规范》(第一册 土建工程 JTG 3370.1-2018)、SL 279-2016《水工隧洞设计规范》的建议公式,进行了适用性分析与比较,明确了《公路隧道设计规范》中给出的建议公式概念明确,适用范围较为广泛,但由于隧道在深、浅埋段采用了不同围岩压力计算方法,导致深、浅埋交界处出现围岩压力突变现象,还需对理论解析进一步修正与完善;顾鑫杰[4]等人对山岭隧道塌方成因进行了分析,认为在浅埋松散段可采用普氏压力公式计算围岩压力,而对于Ⅰ~Ⅳ级围岩仅考虑形变压力。以往研究的内容未反应规范中公式的不足或解决方法。
现针对规范计算方法存在的上述问题,通过举例分析,提出较合理的计算方法。以双车道开挖宽度9 m≤Bt<14 m为例,探讨合理的围岩压力计算方法。参考规范建议值,Ⅳ级围岩计算摩擦角取φc=50°~60°,θ=40°~48°,γ=21 kN/m3;Ⅴ级围岩计算摩擦角取φc=40°~50°,θ=24°~30°,γ=18 kN/m3;Ⅵ级围岩计算摩擦角取φc=30°~40°,θ=12°~16°,γ=16 kN/m3。
hq=0.45×2s-1ω
(7)
式中:s为围岩级别;ω为隧道开挖宽度影响系数。
计算得深、浅埋分界深度分别为:Ⅳ级围岩为12.5~17.1 m;Ⅴ级围岩为25.2~34.2 m;Ⅵ级围岩为50.5~95.75 m。采用上述公式分别对双车道浅埋段Ⅳ~Ⅵ级围岩压力进行了计算,取H=hq,得到q浅1、e浅1;H=2.5hq,得到q浅2、e浅2,结果见表1。不同跨度,各级围岩压力与埋深的关系见图2~4。
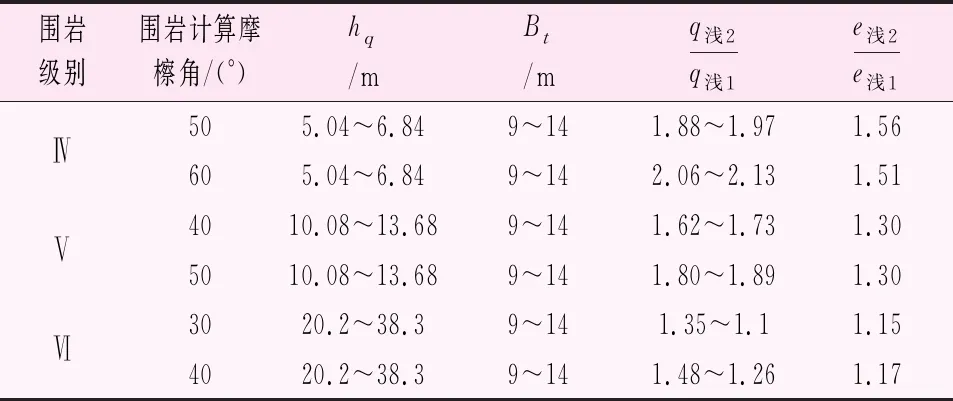
表1 Ⅳ~Ⅵ级围岩浅埋段围岩压力计算表

图2 浅埋段Ⅳ级围岩竖向荷载与埋深关系图
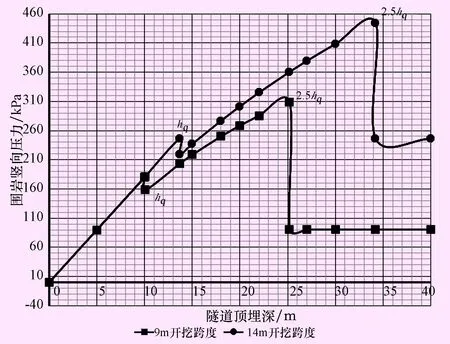
图3 浅埋段Ⅴ级围岩竖向荷载与埋深关系图
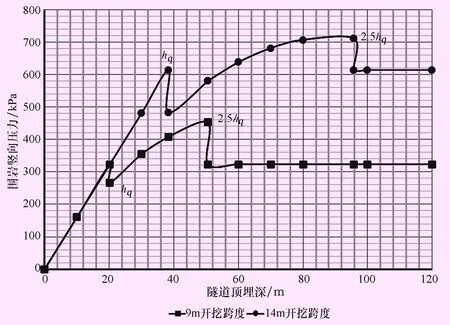
图4 浅埋段Ⅵ级围岩竖向荷载与埋深关系图
从表1可以看出围岩级别越高,浅埋段围岩压力比值越小;Ⅳ~Ⅴ级围岩竖向压力q浅2与q浅1比均值达1.88,侧压力e浅2与e浅1比均值达1.42,而Ⅵ级围岩两者竖向压力比均值为1.22(最低1.1),侧压力比均值为1.16。
从图2~3可以看出:
(1) 对于Ⅳ~Ⅵ级围岩,均在洞顶埋深hq、2.5hq处,即超浅埋与浅埋、浅埋与深埋交界面,围岩压力出现突变,深、浅埋交界面处突变最大。
(2) 同跨度情况下,洞顶埋深在hq (3) 从图3可以看出,Ⅵ级围岩埋深hq以上部分围岩压力增长缓慢,逐步稳定,且深、浅埋分界处围岩压力没有较大突变,与工程实际较吻合。 产生上述偏差主要原因为规范中针对浅埋段围岩压力的计算公式假定条件不尽合理: (1) 规范中在不同区段采用了不同的计算理论:超浅埋段采用全土柱理论,浅埋段采用了谢家烋[5]理论,深埋段采用了铁路隧道经验公式,导致三区段交界面处出现突变。 (3) 浅埋段洞顶围岩均按松散体考虑,提出了“全高度松散压力”的理论公式,即洞顶以上均为连续塑性松动区,这也是从洞口安全角度考虑,将浅埋段以塌落拱矢高为界,至深、浅埋分界范围内的围岩均视为松散塌落范围。实际浅埋段在开挖前或过程中对围岩采取了超前加固措施,且在开挖后及时施做了支护系统,很大程度约束了围岩变形,并在洞顶以上一定厚度变形逐渐趋于稳定。可以理解为隧道开挖后仅在塌落拱范围内形成塑性松动区,以外区域为逐渐趋于稳定的弹性区,该区域将会产生形变压力[6]。 为此,对于浅埋段Ⅰ~Ⅴ级围岩埋深hq (8) 式中:Pi为作用于隧道结构上任意一点形变压力, kN/m2;P0为隧道深处原始地应力,kN/m2;c为围岩的粘聚力,kN/m2;φ为围岩内摩擦角,°;a为隧道开挖半径,m,当隧道接近圆形断面时,可以直接开挖跨径或高度作为拟合断面直径;当与圆形断面差异大时,可以按采用开挖断面的最小外接圆作为拟合断面;R为隧道开挖后形成的塑性区半径,m;取hq与a之和。 另外,从安全及便于实施角度考虑,洞口浅埋段应以合理的围岩压力进行支护与衬砌结构设计,统一结构设计参数,即超浅埋与浅埋段间取大值。 通过上述对山岭公路双车道浅埋段围岩压力的规范计算方法进行数据分析与论证,得出以下结论。 (1) 当埋深H小于或等于hq时,按规范计算的Ⅰ~Ⅵ级围岩压力基本与实际吻合,且与经验结构参数匹配; (2) 当hq (3) 公路隧道洞口浅埋段深、浅埋分界合理,浅埋段取围岩压力相对大值,并对结构进行统一设计,以便实施。
3 结 论
