多站融合情况下云数据中心的功率分配方法

2021-11-29张正文孙树娟

能源与环保 2021年11期

张正文，李津，孙树娟

(国网雄安新区供电公司，河北保定 071600)

随着云服务在互联网上日益占据主导地位，以及基于云服务的物联网的出现[1-4]。预计到2021年，云数据中心流量将占数据中心总流量的95%[5]。随着万物物联理念的提出，电网作为传统行业，也在积极的对自身进行升级和改革[6-7]。为了解决海量数据处理造成的流量大、时间长等问题[8-9]，在此智能电网引入了多站融合的概念，通过将分布密集的变电站建设运营成为数据中心等，从而解决该问题。但一个数据中心拥有数千台服务器、存储设备、冷却设施和电力变压器，数据中心部门估计占全球电力消耗的1.4%。如果直接将变电站转化为数据中心，而不是考虑给其分配有限能量，这可能导致发电站超载，对电网造成严重破坏，同时，还可能剥夺更需要电力的其他数据中心的能量。为了克服这一问题，提出了一种针对数据中心用电量的博弈论方案(G-Power)，其中每个数据中心由博弈中的一个参与者表示。该方案的基本思想是根据数据中心的收费优先级、关键运行应用程序的优先级和其他数据中心的优先级3个指标为每个数据中心分配最优的功率，以达到公平的功率分配。

1 系统结构与问题表述

在提出的系统中，智能电网控制器(公用事业公司)负责供电，响应用户的用电需求。电力来自与云数据中心通信的多个发电站(双向通信)。因此，智能电网控制器可以查看每个数据中心的电源行为。智能电网和云数据中心的系统架构如图1所示。

在提出的系统中，数据中心的目标是购买最大功率，以便为其存储的能量充电并处理最大的应用程序。这将提高云提供商的利润。此外，每个数据中心都试图增加其充电状态并以自私的方式要求电力，而不考虑计划用于数据中心的有限能源。这可能使发电站过载，并对电网造成严重损害。

2 G-Power模型建立

2.1 博弈描述

在这里介绍了G-Power的原理，首先用非合作博弈理论对数据中心的功率分配进行了建模。因此，考虑对策：G=(I，Si，gaini)i∈T，其中I表示一组玩家(数据中心)，d1，d2，…，dn，其中n是参与博弈的数据中心的数量。

在提出的方案中，设计了回报函数来反映4个主要函数：第1个函数计算数据中心对具有高功率的需求(效用函数)；其余3个函数是优先级成本函数，分别计算数据中心收费优先级的成本、关键应用程序优先级的成本以及总关键应用程序优先级的成本。支付函数包括以下4个函数。

(1) 效用函数。在G-Power中，效用函数被建模为，当每个参与者增加其电力需求值时，会获得更多的利润。在网络研究中常用的效用函数[16]，选择使用对数函数来设计G-Power的效用函数。因此，选择一个效用函数：

γi(xi)=log(xi+1)，∀i∈I

(1)

式中，xi为玩家di需求的电量。

(2)数据中心的费用函数优先权。该函数定义了玩家根据其电量需求xi和其收费优先级Dvi支付的惩罚。在提出的方法中，优先级是根据活跃服务器ASi和玩家di的荷电状态SoCi计算的，具体公式见式(2)：

(2)

因此，有以下函数：

ρi(xi，Dpi)=xi×Dpi

(3)

(3)关键应用程序优先级的成本函数。在这个优先级成本函数中，考虑了一个玩家di的关键运行应用程序。在G-Power中，将实时应用程序视为关键应用程序。该功能基于玩家的电量需求xi及其关键应用优先Api。将优先级Api计算为关键应用程序记录Critical_appsi占总应用程序记录Total_appsi的比率。因此，定义函数如下：

σi(xi，Ani)=xi×Ani

(4)

(5)

(4)总关键应用优先级的成本函数。该优先级成本函数基于玩家功率量需求xi及其总关键应用优先级TPi。优先级TPi是玩家关键应用与所有玩家关键应用之和的比率。因此，有以下成本函数：

τi(xi，Tpi)=xi×Tpi

(6)

(7)

在定义了玩家di的4个函数之后，可以得出支付函数：

gaini(xi，x-i)=αiγi(xi)+βiρi(xi，Dpi)+ωiσi(xi，Api)+ψiτi(xi，Tpi)

(8)

其中，x-i={xk}(k∈i)且是除玩家di外的所有玩家的电力需求量(策略)向量。s=(xi，x-i)是策略配置文件。αi，βi，ωi和ψi分别是γi，ρi，σi和τi的玩家偏好系数。这些参数的设置是为了满足系统的目标和要求，例如，当ωi值越大，获得具有高关键应用率的玩家和那些具有低关键应用比率的玩家的功率之间的差异就越大，反之亦然。

2.2 纳什均衡

在博弈论中，纳什均衡(NE)是一个基本概念，常用于预测所有参与者的未来行为和确定永久状态。这意味着博弈中的每个玩家都没有兴趣改变自己的策略，并执行相同的操作。因此，如果存在一个NE，则非合作博弈有一个解。在G-Power的对策G=(I，Si，gaini)i=T中，如果没有一个玩家能够通过改变策略来增加其收益，那么一组策略代表一个NE。

(9)

综上所述，在计算G的对策解之前，证明了NE的存在性和唯一性。

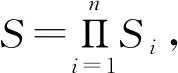
当时，每个参与者的策略集是闭有界的。那么，集合Si，∀i∈I是紧的。

考虑2点y1，y2∈Si和ε=[0，1]。因此，得到

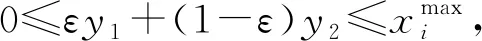
通过计算s={xi}，∀i∈I的增益的Hessian矩阵，可以证明的支付函数的凹性如下：

(10)

(11)

因此，可以看到H(S)对于所有策略s∈S是负定的，因此，gainxi，x-i)在Si，∀i∈I中是严格凹的。根据Nikaido-Isoda定理[10]，G-Power的博弈G至少具有一个NE。

(2)纳什均衡的唯一性。设u=(u1，u2，…，un)是正参数的随机向量，使用Rosen定理[11]来得到支付函数的加权正和，其定义如下：

(12)

这里δ(xi，x-i；u)伪梯度给出的：

(13)

并且

(14)

另外，g的Jacobian矩阵J(xi，x-i；u)可以定义如式(15)所示。

(15)

式中，Bij=uiDij，∀i，j∈I。

由此可见，对于所有对称矩阵是负定的。因此，函数是根据Rosen定理(18)对角线严格凹的。因此，博弈G在其纯策略空间中具有唯一的NE，这也符合Rosen定理。

(16)

约束条件为：

为了解决问题(F)，使用拉格朗日乘子法使G-Power的函数在2个不等式约束下最大化。引入了2个拉格朗日乘子λi和li，函数可定义为式(17)：

(17)

因此，对于每个玩家di，G-Power的拉格朗日函数满足以下KKT条件，如式(18)所示：

(18)

(19)

在这里条件1和条件2可以用公式(20)和(21)表示：

βiρi(xi，Dpi)+ωiσi(xi，Api)+ψiτi(xi，Tpi≥αi

(20)

(21)

3 实验仿真与结果

3.1 实验设置

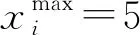
3.2 结果与评估

图2分别使用式(2)、式(5)和式(7)显示了每个数据中心在1 d内不同的成本(数据中心的费用优先级、关键应用程序优先级和总关键应用程序优先级)。

图2 数据中心成本变化

可以观察到，在每个数据中心，数据中心的收费优先级在非高峰时段较低，而在高峰时段较高。这可以解释为这样一个事实：数据中心没有太多活动服务器，在非高峰时间存储能量，相反，在高峰时间，数据中心已对其能量进行了充电并拥有大量活动服务器。另一方面，关键应用程序和总的关键应用程序优先级在非高峰时段较高，而在高峰时段较低。这意味着，与数据中心中运行的应用程序总数相比，在高峰时段运行的关键应用程序要比在非高峰时段运行的应用程序多得多。

图3描述了使用基于博弈的功率分配方案在一个特定小时内(0：00)4个数据中心的功率分配。可以看到，G-Power方案根据每个数据中心的优先级成本进行了公平的分配。

图3 基于博弈的电量分配

与自私方案的性能比较如图4所示。

图4 与自私方案的性能比较

图4(a)显示了随机选择的一个数据中心，G-Power与自私方案的功率分配比较。可以观察到自私方案总是以所需的总功率供应，而不管数据中心有什么关键应用或能量消耗。这可能会使电网过载并使发电站超载。另一方面，在G-Power中分配的能量随着时间的推移而变化，可能会减少到1.27 MW。这通常发生在非高峰时段(例如图4(a)中的3：00)，此时数据中心正在充电，并且没有很多正在运行的应用程序。此外，它可能会达到最大值5 MW，如上午11：00和19：00。所呈现的结果是由于提出的方案中使用的博弈论，该方案考虑到：①每个数据中心的活动服务器和充电状态；②在数据中心运行的关键应用程序；③在所有数据中心运行的关键应用程序，如图4(b)、图4(c)和图4(d)所示。在图4(b)中显示了根据数据中心在活动服务器和充电状态方面的收费优先级的功率分配值。可以看到，在G-Power中，分配的电力随着优先级的降低而减少。然而，自私方式方案在不考虑任何优先级的情况下，总是具有稳定的功率分配。此外，图4(c)和图4(d)还表明，关键应用程序优先级和总关键应用程序优先级分别与功率分配成反比关系。当一个玩家的关键应用程序增加时，它的能力就会增强，反之亦然。