基于虚拟样机的行星齿轮系统参数化建模及故障分析
2021-11-29刘奇洪赖展宇陶鸿景化一行
刘奇洪 , 赖展宇 , 陶鸿景 , 王 帅 , 化一行
(中国矿业大学(北京)机电与信息工程学院,北京 100083)
0 引言
机械行业中使用最广泛的传动方式就是齿轮传动。通过行星齿轮与定轴齿轮的对比,不难发现行星齿轮拥有多个优点,其中最显著的就是在传递动力的时候能够起到功率分流的作用,并且输入轴和输出轴在同一水平线上。因此,在实际机械应用当中,行星齿轮大量应用在复杂的大型机械装备中,如风力发电、工程机械、直升机等。
但是,在现实中存在着很恶劣的工作环境,尤其是低转速重载荷的情况,再加上机械系统中的行星齿轮由于制作过程中的误差和装配误差而导致频繁振动,因此,系统很容易出现裂纹、点蚀和脱落等局部故障。局部故障通常会逐步加剧,最终导致齿轮断裂的情况发生。行星齿轮机构的齿轮一旦发生断裂,会严重地影响整个机械系统的运转并造成严重的财产损失,更重要的是机械机构的运行乃至工作人员人身安全都会受到威胁。
因此,国内外学者对行星齿轮系统动力学特性及故障诊断进行了大量研究,并且已经取得了丰富的成果[1-3]。而目前对行星减速轮系的建模分析大多都是建立在正常状态下,缺乏对故障状态下的行星轮系建模研究[4]。Ericson等考虑了行星轮轴承径向和切向承载情况,计算了两个方向上轴承刚度并引入模型中,研究行星齿轮传动各阶固有频随负载的变化[5]。Liang等在建立行星齿轮传动系统动力学模型时,引入了啮合间的相位差,分析了在太阳轮出现裂纹时的时变啮合刚度[6]。Zhang等分别采用集中质量模型和有限元模型,对两级行星齿轮传动动态特性进行对比分析,研究了各刚度对系统振动模式的影响[7]。
随着计算机仿真和虚拟样机技术的发展,如今可通过建立齿轮传动系统的虚拟样机模型,对系统动力学响应特征进行分析[8]。因此,笔者在前人研究的基础上,利用虚拟仿真对故障行星齿轮系统进行动力学特性分析,并进行了动力学仿真,希望为后续进行行星齿轮故障时的动力学分析和故障所需诊断提供可靠的理论支持。
1 含断齿故障行星齿轮系统实体模型建立
1.1 建立故障行星齿轮系统各部件模型
本研究通过使用UG软件开展对行星齿轮的建模工作,所具有基本参数如表1所示。

表1 基本参数表
1.2 齿轮的装配
在UG中建模和装配,本研究主要对太阳轮的断齿在恒速恒载、恒速变载、变速恒载、变速变载的情况下发生故障的齿轮所具有的动力特性进行研究。
故障齿轮建模如图1所示。
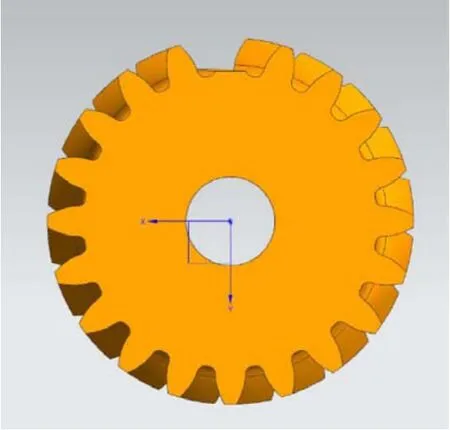
图1 太阳轮断齿
太阳轮断齿后装配图,如图2所示。
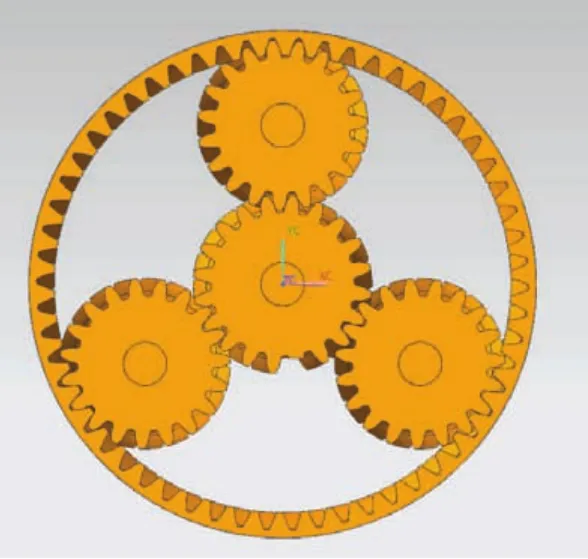
图2 装配图
2 故障行星齿轮系统动力学分析
2.1 故障行星齿轮系统动力学模型的设置
将模型在UG中保存后导入到Adams中,设置太阳轮与地面转动副,行星架与地面转动副,行星轮与行星架转动副,内齿圈与地面固定副,重力参数后得到如图3所示的模型。
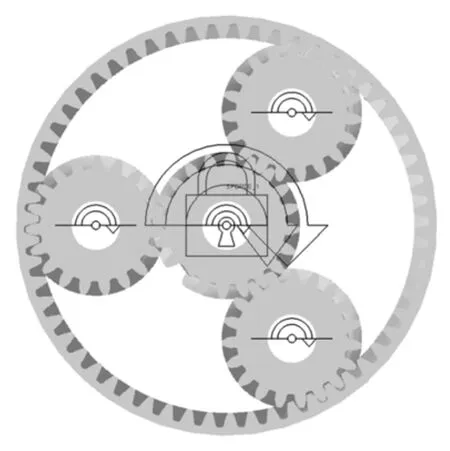
图3 模型与旋转副
2.2 参数计算
2.2.1 特征频率的计算
转速和齿数都会影响齿轮的啮合频率,在此系统中太阳轮、行星轮、齿圈的啮合频率均为
断齿故障是齿轮严重故障种类之一,断齿故障产生时,齿轮啮合会在断齿处产生冲击振动。而在齿轮的旋转中,按照一定的时间间隔会有规律地重复出现冲击。而此时存在故障的行星轮需要和太阳轮、齿圈分别啮合,如此就会导致在断齿处有两个不同的冲击。此时行星轮的局部故障特征频率为
经过计算得出行星齿轮系统的啮合频率:fm=61.96 Hz。
太阳轮局部故障特征频率:fp=3.1 Hz。
2.2.2 接触力的计算
实际上多由在齿顶处啮合的轮齿分担较多的载荷,为便于计算,通常按全部载荷作用于齿顶来计算齿根的弯曲强度。接触力的计算公式如下:
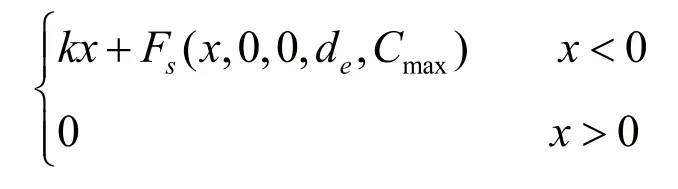
式中:k——啮合刚度;
x——齿间距离;
e——非线性指数;
Fs——阶跃函数;
Cmax——达到最大穿透深度时的最大阻力;
de——最大阻尼时的击穿深度。
最终得出刚度如下。

3 仿真运动分析
3.1 仿真条件设置
由于采用MMKS单位制(以mm为长度单位),以下长度单位均使用mm。
1)添加行星轮与太阳轮的接触:由接触力计算结果得到刚度为力指数为1.5,阻尼为95 N·s/mm,穿透深度为0.1 mm。
2)添加行星轮与内齿圈的接触:由接触力计算结果得到刚度为力指数为1.5,阻尼为160 N·s/mm,穿透深度为0.1 mm。
3)添加负载力矩:为了使得在仿真过程中负载不发生突变,防止仿真数据异常,同样选择使用step函数,将负载力矩在0.2 s内由0增加至1.79×107N/m。
3.2 正常行星齿轮系统的仿真
正常行星齿轮系统中的太阳轮输入转速图像如图4所示,在0.2 s时加速到了1 500°/s,符合由step函数添加的转速驱动。

图4 太阳轮输入转速曲线
行星架的输出转速曲线如图5所示,由理论计算所得行星架理论转速应为384.6°/s,在仿真得到的曲线中,速度稳定后的行星架角速度均值约为384°/s,基本符合理论计算。

图5 行星架输出转速曲线
在正常行星齿轮系统中,行星轮和太阳轮啮合力幅值的时域和频域曲线如图6所示。
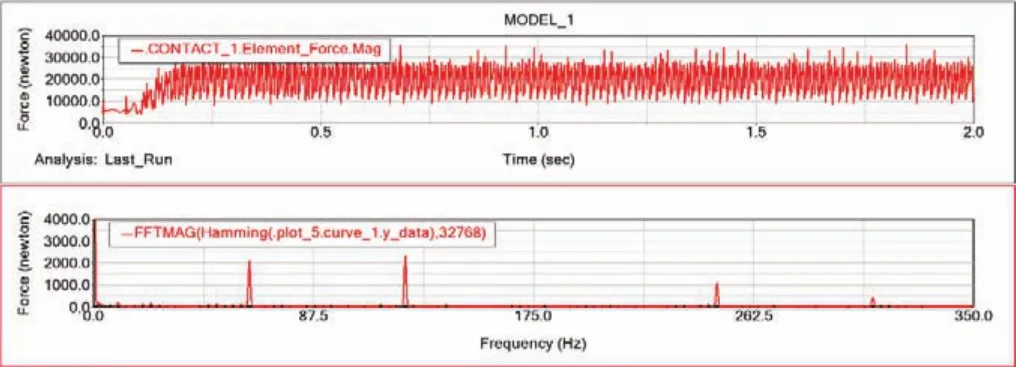
图6 行星轮太阳轮啮合力幅值的时域和频域曲线
由啮合力的时域曲线可知啮合力的均值为21 816 N,其频谱的峰值61.97 Hz及其倍频成分,基本符合理论计算中行星轮系啮合频率(61.96 Hz)及其倍频成分。
3.3 太阳轮单齿断齿故障的行星齿轮系统仿真
3.3.1 恒速恒载时太阳轮单齿断齿故障时的时域频域分析
在恒速恒载情况下发生单齿断齿故障时,太阳轮与行星轮啮合力的时域频域曲线如图7所示。
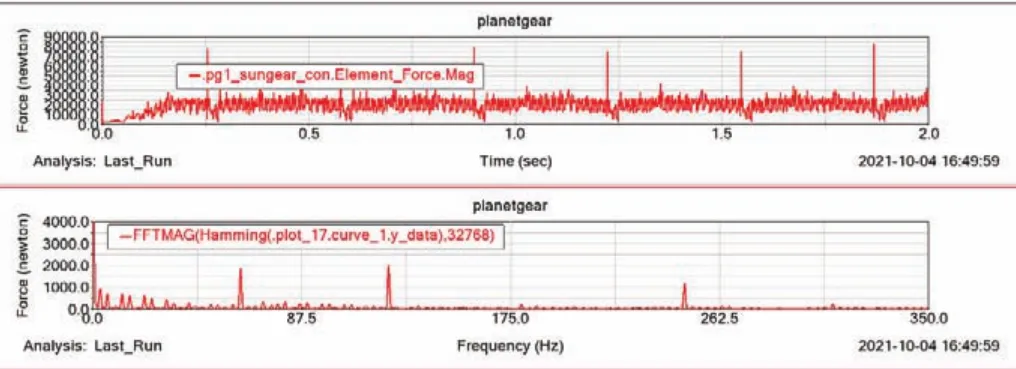
图7 恒速恒载时太阳轮单齿故障的啮合力时域频域曲线
除去冲击,其啮合力均值为21 260 N,冲击间隔为0.322 7 s,啮合频率前的边带成分第一个峰值出现在3.35 Hz处,大小为953.94 N;第二个峰值出现在6.1 s处,大小为733.84 N。此后的边带成分都以此规律分布,逐渐递减。图7中显示出断齿使得行星轮系运行过程中发生了强烈的冲击,且在频域曲线的低频区域产生了较为明显的边带成分。
3.3.2 恒速变载时太阳轮单齿断齿故障时的时域频域分析
在恒速变载情况下发生单齿断齿故障时,太阳轮与行星轮啮合力的时域频域曲线如图8所示。载荷以正弦周期变化,周期为4 s,峰值仍为1.79×107N/m。
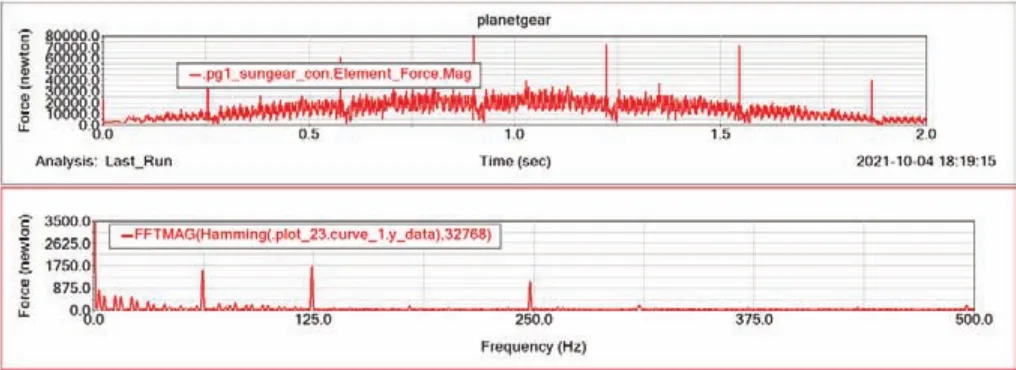
图8 恒速变载时太阳轮单齿故障的啮合力时域频域曲线
图中曲线显示出在负载逐渐增加的过程中,断齿带来的冲击强度越来越大,且在低频区域会产生较为明显的边带成分,边带成分频率的分布规律与恒速恒载时相似。
3.3.3 变速恒载时太阳轮单齿断齿故障时的时域频域分析
在恒载、速度以正弦量变化的情况下发生单齿断齿故障时,太阳轮与行星轮啮合力的时域频域曲线如图9所示。其中,速度为正弦周期变化,周期为4 s,峰值仍为1 500°/s,其行星架速度响应曲线如图10所示。
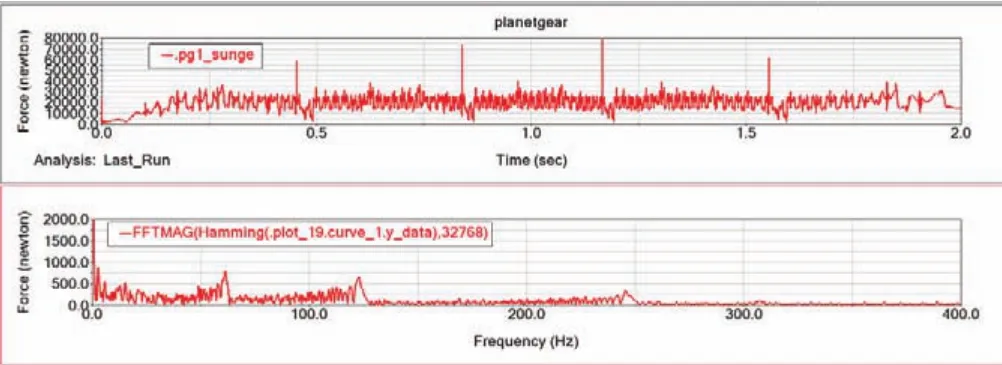
图9 变速恒载时太阳轮单齿故障的啮合力时域频域曲线

图10 行星架速度响应曲线
如图所示,由于负载恒定,即使在低速区也产生了同样大小的冲击,但由于速度变化导致啮合的峰值频率在不断变化,导致虽然能辨别出处于最大速度时的峰值频率,但边带成分极为明显。
3.3.4 变速变载时太阳轮单齿断齿故障时的时域频域分析
在变速变载情况下发生单齿断齿故障时,太阳轮与行星轮啮合力的时域频域曲线如图11所示。载荷以正弦周期变化,周期为4 s,峰值仍为1.79×107N/m;速度为正弦周期变化,周期为4 s,峰值仍为1 500°/s。
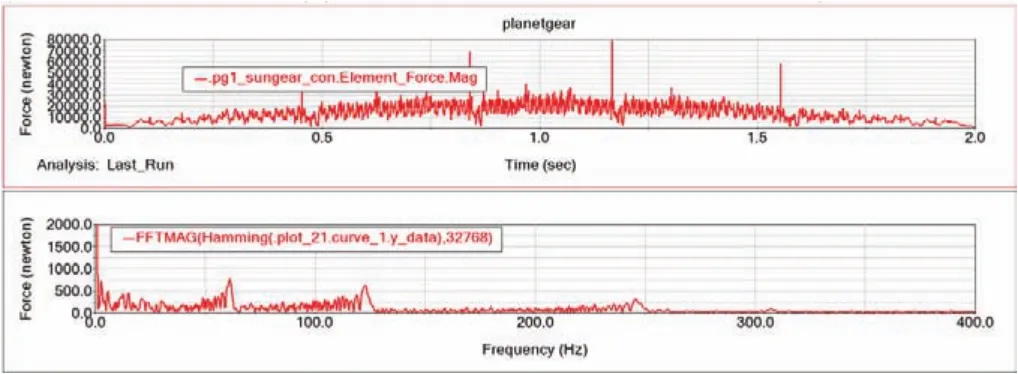
图11 变速变载时太阳轮单齿故障的啮合力时域频域曲线
如图11所示,冲击随着负载的增大而增大;同样的,由于速度变化,啮合力峰值频率也在变化,导致边带成分极为明显。
4 结语
1)本研究采用UG建模,基于ADAMS软件对行星齿轮以及太阳齿轮断齿故障进行了动力学仿真,通过采集齿轮的振动信号和频谱特性,定位故障位置。
2)通过分析和对比正常行星轮系与故障行星轮系的啮合力幅值与频谱曲线得出,当齿轮发生断齿故障时会导致啮合力产生周期性冲击,其啮合力幅值与频率曲线与正常情况偏离。且在变速变载等情况下,故障齿轮处于变速的情况下其啮合力幅值频率曲线的偏离程度最高。
3)根据以上结论,在分析故障行星轮减速系统时,可以通过分析其啮合力幅值频率曲线来判断该系统是否存在特定的故障。
