发展数学核心素养的三个支点：爱提问、善思考、会探究

梁伊媛

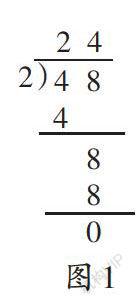
[摘 要]课程改革背景下，以个人全面发展和终身学习为主体的核心素养逐渐取代了以学科知识结构为主体的传统课程标准体系。通过理论研究并结合工作实践，从爱提问、善思考、会探究三个角度论述了发展学生数学思维力，培养数学核心素养的基本路径，为培养学生的核心素养添砖加瓦。

[关键词]核心素养;笔算除法;动手操作

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）32-0085-02

核心素养是一个综合性的概念，它指的是学生在学习中逐步形成的适应个人长远发展和未来社会发展所需的关键能力。从整体上来看，思维能力是数学核心素养的重要组成部分，要培养学生的核心素養，发展学生数学思维能力是至关重要的环节。笔者通过理论研究并结合工作实践，从爱提问、善思考和会探究三个角度论述了发展学生数学思维力，培养数学核心素养的基本路径。

一、爱提问，在增强学生“提问力”中发展素养

学起于思，思源于疑。问题是学生学习和思考的原动力。当学生在思考中产生疑问时，就会引发提出问题、解决问题的动力，可见，由认知失衡到认知平衡的过程实际上就是提问和释疑的过程。学生主动提出问题，是学生掌握学习主动权的生动体现。与解决他人提出的问题相比，主动提出问题并解决，更能使学生产生真正的学习需求，成为一个学习者和思考者，进而迸发出更大的创造力，实现学生核心素养的提升，对此，发展学生的提问能力是顺应儿童天性的需要。小学生活泼好动，对陌生事物往往具有强烈的好奇心。正是在这种好奇心的驱使下，他们才会对未知事物提出问题，并借助一个个问题，在已知世界与未知世界中建立某种联系，从而增强自身学识，发展自身能力，提升核心素养。

例如，教学两位数除以一位数的笔算时，引导学生理解除法竖式的算理和算法是本节课的核心。教师首先引导学生把48根小棒（10根1捆的有4捆，单独的有8根）平均分成2份，每份是2捆零4根，即24根小棒。在此基础上，教师为学生呈现48÷2的竖式计算过程（如图1所示）。

师：对于48÷2的竖式计算，同学们有什么疑问？

生1：为什么要把“2”写在商的十位上，把“4”写在商的个位上？

生2：除法竖式和我们刚才摆小棒的过程有什么关联？为什么要先摆小棒，然后再学习除法竖式？

师：同学们的问题提得很好。有没有哪位同学能够为大家答疑解惑呢？

生3：把4捆小棒平均分成2份，每份是2捆，即20根小棒，所以要把“2”写在商的十位上，表示2个十，即20。把8根小棒平均分成2份，每份是4根小棒，所以把“4”写在商的个位上，表示4个一，即4。

师：这个解释非常生动易懂。谁能解释另一个问题呢？

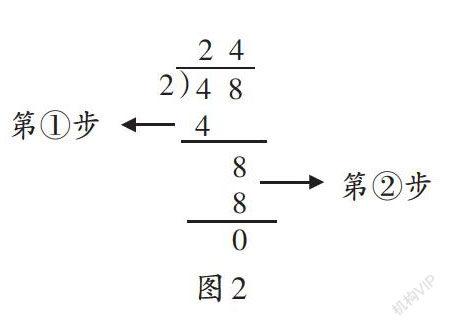
生4：我认为除法竖式可以分成两步，这两步与摆小棒的过程是对应的（如图2所示）。第①步表示把4捆小棒平均分成2份，每份2捆;第②步表示把8根小棒平均分成2份，每份4根。

生5：是啊，除法竖式是摆小棒过程的另一种表达方式，先摆小棒再学竖式，使得理解除法竖式问题变简单了。

师：同学们还有什么疑问吗？

生6：在这道题中，4捆小棒平均分成2份，每份刚好2捆，但是如果是5捆零8根小棒又该怎么分呢？换句话说，58÷2该怎样列竖式呢？

……

问题不会凭空产生，它必然借助于某种知识载体和现实情境酝酿而生。教学中，教师首先引导学生通过数学操作初步认识了48÷2的计算过程，这就为学生的下一步提问准备了知识条件。在此基础上，教师呈现除法竖式计算，给予了学生思考的空间，促使学生主动提问，让提问与释疑有机结合。教学中，学生是提问的主体，同时也是答疑解惑的主角，教师仅仅是学生学习活动的组织者和指导者。学生在提问和释疑过程中，获得的不仅仅是问题与答案本身，同时也看到了别人发现问题和提出问题的视角，由此提问能力也得到了发展。

二、善思考，在提升数学“思考力”中发展素养

法国作家法朗士曾云：“形式是一只金瓶，思想之花插入其内，便可流芳百世。”这句话凸显了思考的重要价值。课程标准把“能进行有条理地思考， 能比较清楚地表达自己的思考过程与结果”确立为重要的教学目标。数学思考是一种深层次的、全面的思维活动，数学思考力是一种重要的隐性学力。在小学数学教学中，教师不能仅满足于使学生获得某种知识和技能，更要致力于增强学生的数学思考力，这既是贯彻课程标准的客观要求，也是发展核心素养的内在需求。因此，数学教学必须萌发学生数学思考的种子，积蓄学生数学思考的潜质，引领学生学会数学思考。在实际教学中，首先，教师要创设思考的情境。要使学生学会思考，就要有能够引发学生兴趣的素材，这就需要教师创设真实情境，调动学生思考。其次，教师要关注学生思考的质量。柏拉图曾言，我们应该区分两种不同的存在——经验的存在和理性的存在。经验的存在是有缺陷的，理性的存在才是完美的。这就要求教师要关注学生的思考方式，使学生超越经验化、生活化的认知，直达问题本质，从而让数学思考走向智慧、深刻。

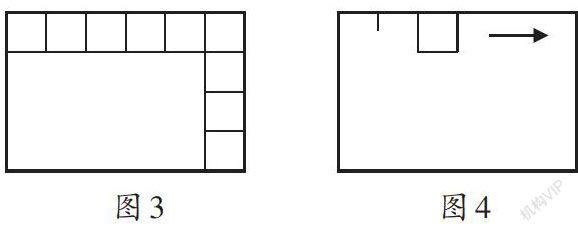
例如，教学长方形的面积时，教师出示了一个长为6厘米，宽为4厘米的长方形，引导学生运用“平铺法”求长方形的面积。学生通过用1平方厘米的小正方形铺满长方形（每行6个，共4行），从而得出长方形的面积是6×4=24（平方厘米），学生由此意识到长方形的面积与小正方形的个数有关。在此基础上，教师进一步把学生的思考引向深处：“我们刚才用了24个小正方形，摆起来用的时间比较长，能够少摆几个小正方形吗？”学生思考，并尝试动手操作。其中一组学生出示了下列摆法（如图3所示）：仅摆出一行一列，就能够用每行个数乘每列个数计算出小正方形的个数。教师并未止步，“还能够再少摆些吗？”这时有小组发现，只用1个小正方形动态量一量长方形的长和宽，也可以知道每行摆几个，一共摆几行，从而求出长方形的面积（如图4所示）。

“学而不思则罔，思而不学则殆。”案例中，教师为学生提供了生动的学习素材，引导学生在操作中思考。从“摆满”到“少摆”再到“只摆1个”，这不仅是学生数学操作上的简化，更是学生数学思维质的飞跃。在这个过程中，学生的思维步步深入，逐渐逼近问题本质，学生的数学思考力在潜移默化中得到了提升，并最终促进了核心素养的发展。

三、会探究，在提升学生“探索力”中发展素养

爱因斯坦曾言，我们体验到的一种最美好、最深刻的情感，就是探索奥秘的感觉，谁缺乏这种情感，他就丧失了在心灵的神圣的颤栗中如痴如醉的能力。数学探究能力是学生学习力的重要体现，也是数学核心素养的重要组成部分。数学学习的过程不应该是一个平铺直叙的过程，而应该是曲折反复的探究过程。探究的过程不是一帆风顺的，在这个过程中，学生或许会遇到各种各样的困惑和问题，但正是这种曲折的探索过程，学生对未知世界的探索力才能得到发展。

例如，教學3的倍数特征时，受2的倍数特征和5的倍数特征的影响，学生一开始把探究的重点放到个位数上，有学生提出：“个位上是3、6、9的数是3的倍数。”这个结论很快被其他学生否定：“27是3的倍数，但是它的个位数字是7;21是3的倍数，但是它的个位数字是1……”教师趁势为学生出示“100以内3的倍数表”（如图4所示），学生发现，3的倍数的个位可能是0至9中的任何一个数字，至此，探索似乎到了“山穷水尽”的境地。这时，教师引导学生转变思路：每个学生先在纸上写出两个3的倍数（两位数和三位数各一个），然后把各数位上的数字调换一下，看看调换后的数还是不是3的倍数。通过探究学生发现，如果一个数是3的倍数，那么不管怎样调换各数位上的数字，这个数还是3的倍数。教师提问：“这说明了什么？”学生讨论后回答：“这说明3的倍数与各数位上的数都有关系。”至此，探索迎来了“峰回路转”，教师指导学生分析自己所写的3的倍数，看看它各数位上数字之和有什么特点？学生通过研究发现，如果一个数各数位上数字之和是3的倍数，那么这个数就是3的倍数。最终，探索迎来了“柳暗花明”的新局面。

数学学习的过程应该是一个探索的过程和再创造的过程。教学中，教师引导学生对“3的倍数特征”展开探索，当学生的思考、讨论陷入僵局，探索陷入“山穷水尽”时，教师及时点拨，巧妙引导，使学生转变思路，最终迎来“峰回路转”，当学生把探索的重点聚焦到“各数位上数字之和”时，探索中“柳暗花明”的新局面就出现了。正是在曲曲折折、反反复复的“真探索”中，学生对知识的认知更深刻了，学生的研究力和探索力也得到了发展。

数学有形， 素养无形。核心素养作为一项综合能力，它的实现必然要依托现实的载体和可行性路径。思维是数学能力之“核”，也是核心素养之“魂”。在笔者看来，爱提问、善思考和会探究是培养学生思维品质，发展学生数学思维，提升学生数学学习力的重要举措，希望更多教师从这三个方面入手，促使课堂成为学生能力和素养生长的“原野”！

（责编 覃小慧）