是泵，不是筛子

阚尚锦

[摘 要]对比“圆的认识”的教学，重点分析如何在课堂教学中培养与提升小学生的数学学习力，让数学学科的教学从被动选拔转变成主动学习。

[关键词]儿童视角;圆的认识;主动学习

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）32-0006-02

当下，课堂教学的研究如火如荼，各种理论层出不穷。作为小学一线数学教师，我在学习了这些理论后得出：数学教学不该是筛选学生的“筛子”，应该是帮助学生经历数学学习过程，激励学生学习的“泵”。本文以“圆的认识”的教学为例，通过对比课堂教学的三个方面，找到激发学生数学学习的动力，进而促进学生自发性学习。

一、教育内容选取关注儿童视角，促进学生主动学习

“圆的认识”这一节课的内容对于学生而言是熟悉的。某次问卷调查中发现，五年级96名学生中，有18.8%的学生认为自己很了解圆，有74.0%的学生认为自己比较了解圆，只有7.2%的学生表示不了解圆。这一数据可以看出大部分学生对“圆”并不陌生。

熟悉的地方往往没有风景，学生在生活中常常会看见圆，因此很多教师的教学会从生活中的圆引入——先给出几张生活中的圆形物体的图片，问学生认不认识，再揭示要学习的课题“圆的认识”，然后通过折叠、测量、对比等方式让学生发现圆的特征，其间穿插教学圆的半径与直径的概念，在一遍又一遍复述“在同圆或等圆中半径都相等”“在同圆或等圆中直径都相等”等概念中结束这一节课。如此教学，学生一般会在教师的精心设计下记住各种概念的条条框框。

很有幸，我读到了特级教师华应龙所著的《华应龙与化错教学》一书。他在书中关于“圆的认识”的教学目标厘定是这样写的：“我思考：半径和直径是不是应该‘浓墨重彩地去渲染？圆的概念都没有给出，是否要咬文嚼字地概括半徑和直径的概念？‘半径都相等和‘直径都相等要不要加上“在同一个圆内或等圆中”？以后再说‘正方形的四条边都相等，还要不要加上‘在同一个正方形呢？数学上的严谨就是这样的吗？这是不是教学内容上的形式主义呢？……”华应龙老师的一系列疑问让我陷入深深的沉思：我们在教学中是不是过于注重所谓的数学的严谨而忽视了儿童立场？在儿童的视角中，圆的特征其实已经无须再通过一系列的动手操作来探究发现，儿童在生活中已经对于圆的特征有所认知，而需要教师重视与提升的是他们在推理、思辨中抽象和概括出这些特征的能力。概念性的课程往往离不开严谨的表述，而儿童的表述是零碎的、不严谨的，所以在这类课程里确实需要教师规范他们的表达，但教师把控的“度”很重要，一不小心就会框住学生，变成形式主义的严谨。

特级教师周卫东说过：“教学中不仅要具有成人视角，在吃透教材编写意图的基础上，还要有具有儿童立场。”记得初为人师的我，课堂上学生迷茫的眼神让我虚汗直冒，作业中学生的错误让我莫名其妙……慢慢地我才明白，曾经的自己仅仅站在成人的角度看待知识、分析现象、解决问题，课堂中的设计、表述和方法都是适合成人认知的，并没有站在儿童的立场用儿童的思维思考和发现，没有用儿童的语言表达和交流，师生都很辛苦：一个辛苦表达而无所授，一个辛苦接受而无所得。因此，要想在课堂中提升学生的数学学习力，教师需要选择好教育内容，而关注儿童视角是基础。

二、教学过程设计把握数学本质，转变课堂研究重点

“圆的认识”这一节课中有许多重要的数学本质，其中最重要的一条就是“圆，一中同长也”。学生只有深切体会到圆的一中同长，才真正把握了圆的本质。但在“圆的认识”教学中常会看到这样的教学场景：

师：刚刚咱们已经了解了圆心、半径和直径，你还知道圆的哪些特征呢？

生1：我知道圆的半径都是一样长的。

师：是吗？请其他同学利用手边的圆片，量一量、比一比，看看他说的对不对。

显然，如此浅显的量一量、比一比等操作是无法让学生深刻感知圆的本质的。

不同于上述教法，强震球老师是这样教学的：

师：学会了画圆之后我们来进行一场比赛吧。请两位同学和我比一比用绳子在黑板上画圆，两位同学一人负责按住绳的这一端，另一人负责画圆。

（教师很快就画好了圆，而两位同学却画不出）

师：你们输了，但你们好像有话要说。

生1：不公平，我们的绳是有弹性的，一用劲，绳的长度就变了，但你的绳没有弹性，无论怎么拉，长度都不会改变。

师：看来想要画一个圆，这个圆的圆心到它圆上任意一个点的距离——

生2：一定要相同，不然就不是圆了。

很明显，强老师紧紧把握住了“圆，一中同长也”这一本质，他巧妙地设计了一个师生比赛，在比赛之初他并没有告诉学生两个画圆工具的区别，为的就是用有弹性的绳画圆打破学生认知的常规束缚。学生在画圆时能够深刻感受到，当绳的长度发生改变时是无法画出圆的，而其他学生也在台上同学喊出“不公平”之后恍然大悟。强老师这样的设计为的就是学生的这一“悟”：原来学生对圆中半径概念的感知只在于文字，只在于它是圆心到圆上任意一点的线段，而并没有真正理解其特征，比赛中的这一“不公平”恰好能够使学生对圆的本质特征产生深刻的认识。

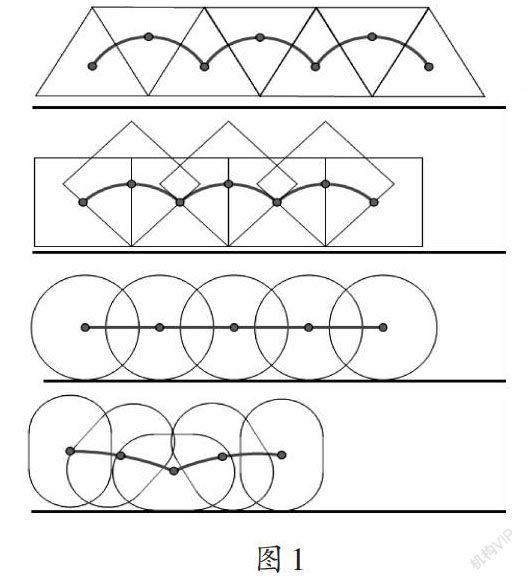
同样，黄爱华老师教学这一课时也很好地把握了圆的本质。他在课上提出了一个问题：“为什么车轮要做成圆形呢？”一石激起千层浪，学生提出各种猜想，在讨论和探究以及动画的演示中学生也逐渐感知到圆与其他平面图形的区别，即圆上任意一点到圆心的距离是一样的，根据这一本质，只有做成圆形的车轮才能保证在车轮旋转的过程中坐在车上的人感到舒适和平稳。动画演示呈现不同图形旋转过程中中心点的变化轨迹（如图1），能够让学生感知到车轮是圆形的表层因素。直观的轨迹让学生更加清晰地发现车轮选择圆形的原因就是圆的本质特征——“一中同长”。

美国数学家赫斯说过：“问题不在于教学的最好方式是什么，而在于数学到底是什么，如果不正视数学的本质问题，便永远解决不了教学的争议。”在教学中想要促进学生学习力的生长，教师需要转变课堂的研究重点，不是教学后以大量低层次的练习来补充课堂，而是要给学生空间和时间研究数学学习内容的本质，让学生亲身感受数学这门学科的魅力。

三、课堂练习优化，促进学生学习力再生长

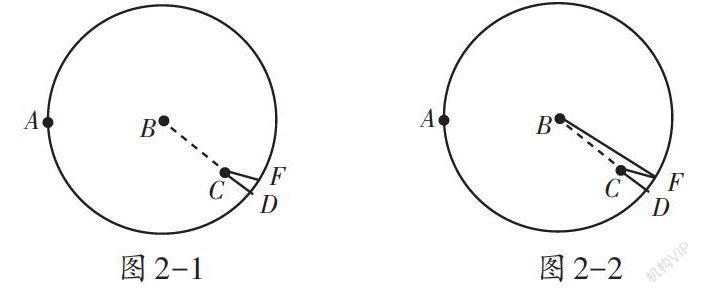
“圆的认识”这一节课的提升练习有很多，但让我眼前一亮的是李培芳老师选取的海上爆破素材，他给出A、B、C三点，以及2条信息和3个问题，让学生自己探究。很快，学生在动手操作后发现C点在以B点为圆心、3 km为半径的圆内，而A点在圆上，因此C点更危险。但当探究到此时在C点的甲该怎样跑时，李老师给出了两种方案供学生选择：沿着半径继续走路线CD;另辟蹊径走路线CF（如图2-1）。学生各执一词，此时李老师没有直接出示答案，而是给予学生充分的时间思考、合作探究。最后大部分学生都选择了路线CD，因为只要连接BF（如图2-2），根据三角形两边之和大于第三边这一特征就可以得知路线CF加路线BC大于半径的长度，而路线CD加路线BC等于半径，因此，选择路线CD。

不同于往常简单的基础练习，这样具有综合性的练习的第一个问题需要学生自己动手画一个以B为圆心、3 km为半徑的圆，画好后还要通过A、C两点与圆的关系来判断，由于A点在圆上，证明A到B的距离恰好是3 km，根据C点在圆内得到CB距离小于3 km，故C点的位置更加危险。经过这一系列的逻辑分析，不仅强化了学生对圆的认识，还提升了学生分析问题的能力。第二个问题的解决对学生的要求更高，需要学生发现题中隐含的三角形，并灵活运用三角形的特征和圆的特征来解决问题。李老师的这一练习融合了三角形和圆的特征，使得学生想要解决每一个问题都要动脑思考。

这样综合性的练习在课堂中是必要的，但这种能够提升学生思维的练习常常会被一些“优秀”学生所垄断，成为个别学生的课堂。对此，李老师让学生小组探究，让每一个学生都试一试、画一画。因此，在班上总有学生解决问题不够灵活时，教师应该反思自己在教学中是否关注到了每一位学生思辨能力的培养，因为每一位学生数学学习力的培养都应该得到重视。

以往的数学教学常常是“筛子”，学生是被动地被选拔，课堂教学常常成为优秀学生展示的平台，而数学学习能力较弱的学生成为课堂中的隐形人，从而导致不少学生害怕数学学习，教师应该及时转变这样的局面，将数学教育从“筛子”转变为“泵”，增强学生的自信心，激发学生学习的动力，让学生的数学学习轻松、快乐。

（责编 金 铃）