大型圆柱壳体装配平台测量系统的误差标定方法
2021-11-27黄维邵吴金波
黄维邵,吴金波
(华中科技大学船舶与海洋工程学院,湖北 武汉 430074)
0 引言
大尺寸精密测量技术已在船舶、航空和高铁等众多工业领域发挥着重要的作用[1]。大型圆柱壳体尺寸庞大、结构外形复杂,在其装配过程中需要通过大尺寸测量系统对壳体任意位置的内径尺寸、板厚、焊缝间隙和板壁差值等数据进行在线测量,以保证装配的精度。当前,龙门式测量机和全站仪都是常用于大型壳体测量的设备[2]。而对于本文研究的装配平台,需实时调整圆柱壳体形状,龙门式测量机由于其自身尺寸结构以及平台装配环境限制,无法满足在装配过程中对壳体尺寸在线测量的需求;而全站仪仅能实现单点测量,无法满足装配过程中对壳体焊缝间隙进行扫描测量的需求,效率较低。
为满足大型圆柱壳体装配平台在装配过程中对壳体尺寸数据进行在线测量的需求,提高测量的效率和精度,本文设计了一种适用于该平台的测量系统。
同时,为了获取准确的壳体内径、板厚、焊缝间隙和板壁差值等尺寸数据,测量系统需满足以下要求:首先,测量机构末端传感器的激光发射点在其基坐标系下的空间位置精度需满足测量需求;其次,测量前需获得大型圆柱壳体实际圆心和测量系统基坐标系原点间的圆心位置误差。针对第1个要求,本文对测量机构展开了误差标定工作:
a.由于硬件加工和安装误差,测量机构运行过程中的几何参数往往和理论值有偏差,称为几何参数误差。
b.为适应装配平台的测量需求,设计的测量机构的尺寸较大,故机械臂在沿立柱轴向平移以及自身伸缩运动过程中,因自重引起的机构柔性变形误差也不可忽略。
依据上述2点,本文建立了测量机构的误差标定模型,通过激光跟踪仪测量出机械臂末端的实际位置,辨识和计算出误差参数,并对误差进行补偿,最终提高了测量机构末端测量点的定位精度。
1 大型圆柱壳体装配平台及测量系统
随着信息技术的不断发展,工业生产制造开始向自动化智能化的方向发展[3]。圆柱类大型壳体的装配一直是工业生产制造过程的难点,其对接质量和效率直接影响到整体生产成本和周期[4]。因此,对圆柱壳体的装配进行研究,将信息化和自动化制造模式引入其生产制造中,提高制造的精度和效率,已成为行业的发展趋势。
本文所研究的大型圆柱壳体装配平台如图1所示。通过自动化调整系统在壳体拼装阶段根据测量机构反馈的数据可实现壳体尺寸的周向调整、顶推调整和径向调整,实现对壳体圆度、垂直度以及壳体间对接纵缝的调节。

图1 装配平台 图2 测量系统
测量系统工作时,通过图2中的升降电机驱动丝杆,控制机械臂的升降运动,完成壳体高度方向上的扫描测量。图3中旋转电机驱动齿轮组控制机械臂在水平面内旋转,完成壳体的环向扫描。测量机构的伸缩机械臂由固定的基础导轨和可移动的一级导轨、二级导轨组成,如图4所示。机械臂伸出时,电机驱动丝杆推动一级导轨向外滑动,使1号滑轮和1号同步带动作,拉动二级导轨同步伸出;反之,机械臂缩回时,丝杆带动一级导轨缩回,2号滑轮和2号同步带动作,拉动二级导轨同步缩回。因此,测量机构可被认为是具有旋转、升降和伸缩功能的三自由度机器人。测量机构的旋转角度通过安装在大齿轮上的编码器测得;升降高度由伺服电机编码器得到;而机械臂的伸长量则通过安装在导轨上的磁栅尺测得。测量机构末端测量点的位置为点激光位移传感器激光发射点的位置。

图3 旋转机构

图4 伸缩机械臂侧视图
2 误差标定
2.1 运动学建模
机器人的运动学误差标定分为建模、误差测量、参数辨识和误差补偿4个步骤[5]。
首先建立测量机构的名义运动学模型,如图5所示。

图5 D-H坐标系
本文以测量机构底座丝杆中心为原点建立基座参考坐标系{O0x0y0z0},以旋转机构中心为原点建立升降机构和旋转机构的坐标系{O1x1y1z1}和{O2x2y2z2},以伸缩机械臂末端点激光位移传感器的激光发射点为原点建立机构末端坐标系{O3x3y3z3}。由图5可知,θ2为x1轴到x2轴绕z1轴旋转的角度,逆时针转动为正,故本文中旋转角度θ2为负值。旋转角度0°位置和-90°位置,如图5所示。
本文采用修正D-H模型进行建模[6],修正D-H参数如表1所示,d1为机械臂高度;θ2为机械臂的旋转角度;d3为机械臂的总长度。
在确定测量机构的修正D-H参数后,即可通过式(1)得到相邻连杆坐标系间的齐次变换矩阵为
(1)
其中,px=aicosθi,py=aisinθi,pz=di,nx=cosθicosβi-sinθisinαisinβi,ny=sinθicosβi+cosθisinαisinβi,nz=-cosαisinβi,ox=-cosαisinθi,oy=cosαicosθi,oz=sinαi,ax=cosθisinβi+sinαisinθicosβi,ay=sinθisinβi-sinαicosθicosβi,az=cosαicosβi。
(3)
(4)
机构末端相对于基座参考坐标系的位姿变换矩阵可由3个相邻连杆坐标系依次相乘得到[7],即测量机构的运动学模型为
(6)

(7)
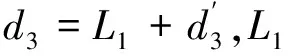
2.2 几何误差建模
从上述运动学模型可知,机构末端位置为机械臂运动学参数的多元函数。假设几何参数误差足够小,则对机构末端的位置进行全微分,可近似得到机构末端的几何参数误差模型为
Δpδ=JδΔq
(8)
Δpδ为几何参数误差引起的末端位置误差;Jδ为误差系数矩阵;Δq为几何参数误差矩阵。
进行冗余性分析后[8],即可得到几何参数误差模型为
(9)
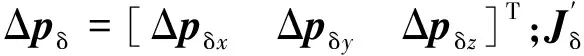
(10)
Δq′=[Δθ1Δa1Δα1Δβ1Δα2Δd3]T
(11)
Jδθ1=[-d30 0]T
(12)
Jδa1=[cosθ20 -sinθ2]T
(13)
Jδα1=[0 -d3cosθ20]T
(14)
Jδβ1=[0 -d3sinθ20]T
(15)
Jδα2=[0 -d30]T
(16)
Jδd3=[0 0 1]T
(17)
2.3 柔性误差建模

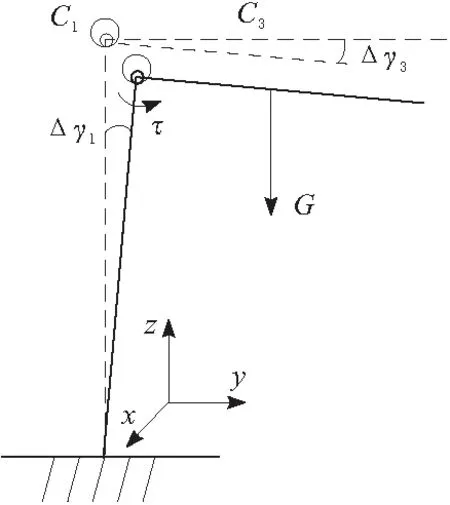
图6 测量机构柔性示意图
(18)
m1、m2和m3分别为基础导轨、一级导轨和二级导轨的质量;L1、L2和L3分别为基础导轨、一级导轨和二级导轨长度,如图4所示。
设立柱柔度为C1,则角Δγ1与弯矩τ之间的关系为
Δγ1=C1τ
(19)
机械臂升降运动时,立柱有效长度的改变导致其柔度的变化。同时,如图5所示,立柱由4根导向杆组成,机械臂绕立柱旋转过程中4根导向杆的受力方向改变,也会导致其整体柔度C1的变化。故升降和旋转机械臂,都会导致角Δγ1的改变。因此,其柔度是关于机械臂高度d1和旋转角度θ2的函数,即
C1=f1(d1,θ2)
(20)
而由材料力学的相关知识可知,当旋转机构角度固定时,立柱柔度可写为与立柱高度相关的线性函数[9],即
C1=k1d1
(21)
k1为与立柱材料和横截面尺寸相关的固定参数。所以,当旋转角度θ2固定时,角Δγ1与弯矩τ之间的关系为
Δγ1=k1·(d1τ)
(22)

(23)

由于几何参数误差、立柱和机械臂弯曲导致的末端位置误差满足线性叠加关系[10-11],则根据几何关系可以得出弯曲偏移角Δγ1和Δγ3带来的末端位置误差为
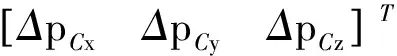
(24)
(25)
cΔγ1为cosΔγ1;sΔγ1为sinΔγ1;sΔγ3为sinΔγ3;cθ2为cosθ2;sθ2为sinθ2。由于偏移角很小,所以cosΔγ1≈1,sinΔγ1≈Δγ1,cosΔγ3≈1,sinΔγ3≈Δγ3,故可将式(25)线性化处理为
(26)
因此,测量机构统一的误差标定模型为
Δp=JΔx
(27)

(28)

JC1=[-d1sinθ2d1cosθ2-d3]T
(29)
JC3=[0 0 -d3]T
(30)
2.4 误差测量、参数辨识及补偿
本文采用激光跟踪仪对测量机构末端测量点的实际位置进行测量,测得的位置坐标pa=[paxpaypaz]T,并结合式(7)的名义运动学模型,得到测量机构末端测量点的位置误差。
将式(10)~式(17)代入式(9),系统几何参数误差模型为
(31)
基于式(31)可知,当机械臂转角θ2和长度d3固定时,改变高度d1,几何参数误差造成的末端位置误差并不会发生变化。而由式(26)可知,当机械臂长度d3不变时,改变高度d1,机械臂弯曲角Δγ3产生的末端位置误差也保持不变。因此,结合统一误差标定模型(27)和式(22)所示的立柱弯曲角Δγ1可知,当机械臂旋转角度θ2和长度d3固定时,升高或降低机械臂引起的末端位置误差的变化是由立柱弯曲角Δγ1的改变导致的。
基于上述结论,使用控制变量法,即可通过如下步骤对测量系统的立柱柔度参数、几何参数误差和机械臂弯曲偏移角进行辨识和计算。
首先,划分机械臂的工作空间。将工作范围在0~-90.00°的机械臂旋转角度θ2分为θ21、θ22、θ23、θ24、θ25和θ26,共6组;将工作范围在467~1 867 mm的机械臂高度d1分为d11、d12、d13、d14、d15、d16、d17和d18,共8组;将工作范围在3 275.00~3 875.00 mm的机械臂长度d3分为d31、d32、d33和d34,共4组。固定机械臂旋转角度θ2和长度d3分别为θ21和d34,测得8组机械臂高度所对应的末端位置误差,根据式(27)建立8组误差方程,即
(32)
Δpz141、Δpz142、Δpz143、Δpz144、Δpz145、Δpz146、Δpz147和Δpz148是高度为d11、d12、d13、d14、d15、d16、d17和d18时对应的Z方向的末端位置误差;Δpδz14为旋转角度θ21和长度d34下由几何参数误差引起的Z方向的末端位置误差;k11为转角θ21对应的立柱柔度参数;τ4和Δγ34分别为长度d34时的弯矩和机械臂弯曲角。建立误差方程后,对式(32)两两作差,消去几何参数误差和弯曲角Δγ34导致的末端误差,则可计算出旋转角度为θ21时的立柱柔度参数k11,即
(33)
而后旋转机械臂至θ22、θ23、θ24、θ25和θ26,重复上述操作,即可计算出6组旋转角度对应的立柱柔度参数k11、k12、k13、k14、k15和k16。通过三次样条插值法[12],即可确定整个0~-90.00°工作空间内的立柱柔度参数k1。至此,完成柔度参数k1的计算共使用了6组旋转角度和8组高度下对应的48组数据。
在得到立柱柔度参数k1后,结合式(27),则几何参数误差和机械臂弯曲导致的末端位置误差Δp′为
Δp′=Δp-JC1k1d1τ
(34)
基于上述48组数据,采用迭代最小二乘法[13],即可对几何参数误差和机械臂长度为d34时的机械臂弯曲偏移角Δγ34进行辨识,辨识算法为:
(35)
(36)
(37)

最后,在得到立柱柔度参数k1和几何参数误差后,固定机械臂旋转角度和高度分别为θ25和d18,依次伸长机械臂至d31、d32和d33,即可得到3组伸长量的机械臂弯曲偏移角Δγ3s,s=1,2,3,即
(38)
Δpz5s8是机械臂旋转角度、高度和长度分别为θ25、d18和d3s时Z方向的末端位置误差;Δpδz5s为旋转角度θ25和长度d3s下由几何参数误差引起的Z方向的末端位置误差;τ是长度为d3s时的弯矩。同理,经三次样条插值即可得到机械臂不同伸长状态下由自身柔度导致的偏移角Δγ3。综上所述,完成测量机构几何参数误差及柔性误差的标定工作,共需测得51组数据。
(39)
3 验证和结论
为证明上述误差标定算法的有效性,选取Leica高精度激光追踪仪ATS600为第3方测量仪器,以其测量数据作为标准数据进行标定和验证。由于激光追踪仪默认的工作坐标系是以其激光出射点为原点的坐标系,因此,试验开始之前要将测量机构基坐标系设置为激光跟踪仪的工作坐标系。激光跟踪仪获取测量机构基坐标系轴线数据后,使用附带的Spatial Analyzer软件即可拟合出测量机构的基坐标系,并将其作为工作坐标系[14]。
实验时机械臂参数如表2和表3所示。

表2 机械臂导轨长度

表3 机械臂质量
根据2.4节中的误差标定方法,并结合测量机构实验现场的工作区间大小、现场试验条件和靶标位置,选取的51组测量点如图7所示。其中,机械臂旋转角度θ21、θ22、θ23、θ24、θ25和θ26分别为-4.24°、-5.24°、-34.10°、-35.10°、-63.90°和-64.90°;机械臂高度d11、d12、d13、d14、d15、d16、d17和d18分别为467 mm、667 mm、867 mm、1 067 mm、1 267 mm、1 467 mm、1 667 mm和1 867 mm;机械臂长度d31、d32、d33和d34分别为3 275.00 mm、3 475.00 mm、3 675.00 mm和3 875.00 mm。立柱柔度参数k1的计算结果如表4所示。

图7 测量点位置

表4 立柱柔度参数计算结果
由于θ21和θ22、θ23和θ24、θ25和θ26的角度值较为接近,为方便计算,选取θ21、θ24和θ263个点进行三次样条插值,可得到不同工作空间内的立柱柔度参数k1取值情况如下所述:
当θ2∈(-90.00°,-64.90°)时,取值为
k1=(0.234 5-0.001 600(θ2+90.00))×10-12
(40)
当θ2∈(-64.90°,-35.10°)时,取值为
k1=(0.194 5-0.001 800(θ2+64.90))×10-12
(41)
当θ2∈(-35.10°,0)时,取值为
k1=(0.175 2+0.001 100(θ2+35.10)-
0.000 100 0(θ2+35.10)2×10-12
(42)
在计算出不同旋转角度的k1后,即可通过式(34)~式(37)对几何参数误差和偏移角Δγ34进行辨识,结果分别如表5和表6所示。
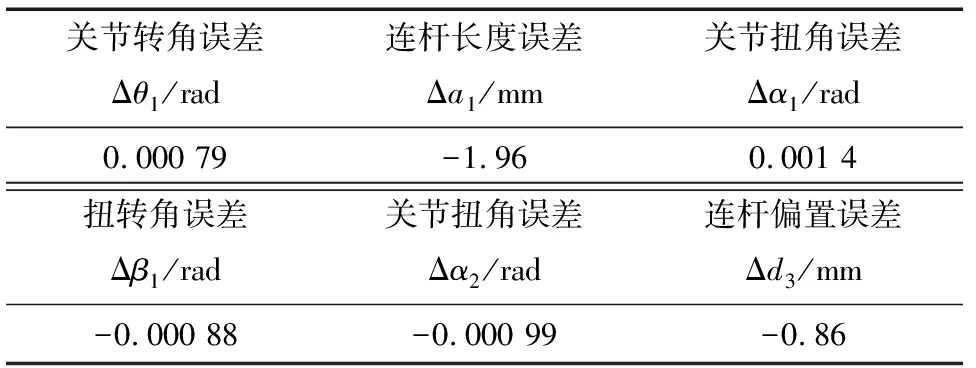
表5 几何参数误差辨识结果
在确定整个工作空间内的vk1和几何参数误差后,通过式(38)计算出机械臂长度分别为d31、d32和d33时对应的机械臂偏移角,计算结果如表6所示。
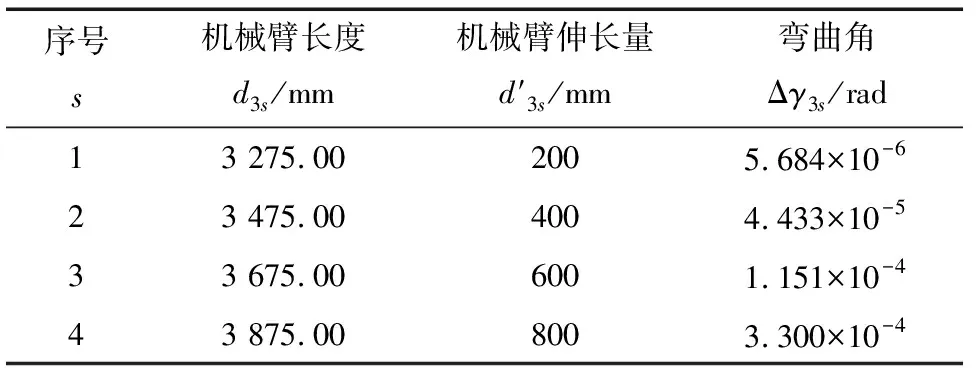
表6 机械臂弯曲角Δγ3
同理,经三次样条插值,得到机械臂伸长量区间内偏移角Δγ3的取值情况如下所述:
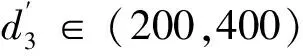
(43)
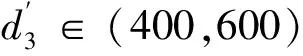
(44)
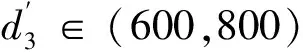
(45)
得到测量系统的几何参数误差Δq′、立柱柔度参数k1和机械臂弯曲偏移角度Δγ3后,即可通过式(39)对上述误差进行补偿。为了验证误差补偿的效果,以式(46)为误差指标重新在工作区间内随机选取5个测量点进行验证,可得测量机构误差补偿前后对比如图8所示。

图8 补偿前后误差对比
(46)
由图8可知,补偿后测量系统末端测量点的定位精度提高至2 mm以内,证明了误差标定算法的有效性。
4 结束语
本文设计了一种适用于大型壳体的尺寸测量系统,分析了系统的误差来源。为保证测量系统末端测量点的定位精度,综合考虑了几何参数误差和柔性误差的影响,提出了误差标定方法,并通过实验验证了标定算法的有效性。
