快速高精度电动调整镜研究

邢海斌，刘力双，夏润秋，陈青山，吕 勇

（北京信息科技大学 仪器科学与光电工程学院，北京 100192）

引言

随着高能激光技术的不断发展，战术激光干扰武器、战略高能激光毁伤武器越来越多地得到应用。高能激光器作为激光武器系统的关键组件，其性能指标尤为重要。单台高能激光器对晶体、光学镀膜等光学元件有较高的技术要求，且体积大、成本高、周期长，限制了其在高能激光武器上的应用。目前，大多采用多台激光器合束的方法实现高能激光的输出。高能激光合束系统光学组件中的反射镜运行时需要满足快速高精度调整的要求，从而精确控制光束传输方向。

光束方向的快速高精度调整方法之一是采用快速反射镜[1]。目前市面上的快速反射镜大多是采用压电陶瓷[2-3]或者音圈电机[4]的驱动方式，以追求高谐振频率，高带宽[5]等指标。例如2004年中科院光电所吴琼雁等人通过优化控制算法将音圈电机快反镜带宽提高到了310 Hz[6]，中国科学院大学的凡木文等人2015年在普通PI 控制方法基础上增加了双二阶滤波器，使音圈电机快反镜与之前相比带宽提高了1 倍[7]。

激光合束系统通常需要在进入工作状态前调整反射镜，在工作过程中不再移动，所以调整镜一般采用步进电机作为驱动机械，微位移机构作为驱动方法。该方法具有较好的分辨率，行程较大，可自锁，工作过程中不需要加电，缺点是会存在机械间隙造成空回[8-9]。

为了减少装备的准备时间，高能激光武器系统的合束系统对反射镜的调整到位时间和精度提出了更高的要求。论文针对该需求设计了一种基于步进电机驱动[10]的大口径二维调整镜，在±500″范围内，调整镜到位时间在3 s 以内，控制误差小于2″，实现了光束小角度高精度的快速调整。论文对系统工作原理和模块设计进行了分析，对系统的控制算法、传感器标定等关键技术进行了研究，采用了S 形加减速控制算法[11-12]与分段线性标定方法，提高了调整镜的调整速度与线性度。

1 调整镜系统工作原理

设计的调整镜系统工作原理如图1所示，调整镜主体效果图如图2所示。系统主要由调整镜主体与驱动控制器两部分组成，其中调整镜主体包括：反射镜模块、刚性支承模块、精密调整机构、精密位移测量模块等；控制驱动器主要由主控模块、驱动模块、通信模块等组成，主控模块接收上位机控制信息，通过控制算法，配合传感器标定，调整镜中反射镜完成偏转，实现对光束的指向控制。

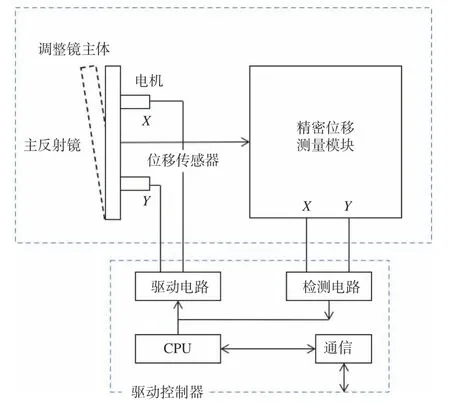
图1 调整镜系统工作原理示意图Fig.1 Schematic diagram of working principle of adjusting mirror system

图2 调整镜主体效果图Fig.2 Effect picture of adjusting mirror main body

2 功能模块设计

2.1 控制模块设计

控制模块中硬件部分主要分为两部分，分别是主控模块与传感器信号检测处理模块。

调整镜的微位移由精密位移测量模块进行检测和位置输出，经由检测电路发送到CPU，CPU 再通过与上位机进行通信，得到目标角度与传感器测得的角度的差值，进行相应算法输出后，使调整镜偏转到相应的角度。

CPU 采用TI 公司最适用于数字控制的C2000系列产品，TMS320F28379S 控制芯片。角度传感器使用电涡流传感器，探头固定于镜面镜托后，信号通过SPI 通信的方式与控制芯片进行通信。步进电机驱动芯片采用DRV8886 芯片，软件部分则主要包括控制算法、上位机控制显示界面。具体工作流程为：激光到达快速反射镜之后，核心控制模块通过USB 接口与上位机通信，实时发送镜面偏转角度；当下位机接收到上位机的位置信号后，通过控制算法驱动调整镜，从而达到控制镜面偏转的效果。调整镜系统上位机操作界面如图3所示。

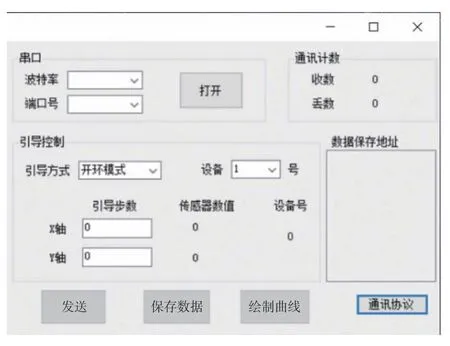
图3 调整镜上位机操作界面Fig.3 Operation interface of adjusting mirror

2.2 控制算法设计

快速反射镜的控制算法一般采用传统的PID 控制算法进行镜面偏转的控制[13-14]。但是，PID 控制算法的缺点是在细分固定的情况下不能同时保证驱动速度和精度。因为项目需求，调整镜需要在精准的前提下快速到位，所以需要采取一种新型的控制方法来解决PID 算法现有的问题。

论文采用S 形加减速算法作为调整镜的控制算法，算法流程如图4所示。首先对调整镜的偏摆角度信号进行采集，之后计算目标值与实际值之间的差值，若是大于1″，则进入变细分算法调节器；若是低于1″，则继续等待下一次目标值。

图4 调整镜控制算法流程图Fig.4 Flow chart of adjusting mirror control algorithm

变细分S 形加减速算法调节器共分为5 个状态：空闲状态、开始状态、加速状态、最大速度以及减速状态。当调节器收到目标位置指令后，调节器会首先进入开始状态，在以1/16 细分控制步进电机转动大约1″后进入加速状态。在加速状态中通过目标值与实际值之间的偏差值计算得到此状态下所需的角度以及步长，然后将步长平均分为4 份，分别使用1/8、1/4、1/2 细分以及全步进状态进行电机控制，之后则进入最大速度状态中。在此状态中再次计算实际值与目标值之间的偏差，得到所需的步长之后，使用全步进方式进行推进，在经过1/4 距离后进入到减速状态。在减速状态中会通过实际值与目标值的偏差将剩下的步长均等的分成4 份，之后分别通过1/2、1/4、1/8、1/16细分进行推进，最终达到目标值。

2.3 系统标定方法研究

传感器标定是指给传感器加上一个标准的被测量，然后调整传感器的某些部件或者软件参数，使得传感器的输出与被测量准确对应[15]。

一般传感器的标定方法采用曲线拟合法进行标定[16]，需要进行米字形采点，之后分别对X轴和Y轴进行公式拟合，最后对标定结果进行检验。对于调整镜来说，因为一体式的机械结构无法使反射镜模块的X轴与Y轴的中心点进行固定，所以在镜面发生偏转的时候，X轴与Y轴会发生耦合，既当X轴电机保持固定的时候，Y轴电机利用推杆推动镜面，同时将中心点向前推进，与此同时，因为X轴推杆处保持不变，并且还有弹簧进行拉紧，所以当仅有一个轴进行开环偏转的时候，另一个轴也会随之发生偏转。因此，在标定时所呈现出来的平面也并不是均匀正交分布的，采点传感器数值平面图如图5所示。

图5 采点传感器数值平面图Fig.5 Numerical plan of sampling point sensor

图5 给出了通过自准直仪标定后的角度分布，其中水平横坐标X轴与竖直纵坐标Y轴为调整镜X轴与Y轴的传感器数值。因为调整镜系统传感器电路中使用的是16 位A/D 转换芯片，所以传感器数值均为0～216之间，也即0～65 535 之间。由于调整镜X、Y轴耦合的原因，图5 中数字①处下方的直线为调整镜X轴传感器采点所形成的直线，数字②处上方的直线为调整镜Y轴传感器采点所形成的直线。利用Matlab 对传感器数值与各点所对应的自准直仪中调整镜真实角度值进行曲面拟合，拟合曲面如图6所示。

图6 整体拟合曲面Fig.6 Overall fitting surface

图6 中AngleX坐标单位为（″），可以看出拟合曲面无法将所有的点准确覆盖住，带来的结果是利用此拟合公式，调整镜大角度偏转出现不线性情况，因此本文提出一种分轴分段线性的标定方法。

分段标定方法共分为3 个步骤：首先在调整

镜±500″范围内均匀采点，将传感器A/D 值与相应的自准直仪呈现出的调整镜偏转角度值记录下来；之后利用Matlab 进行曲面拟合。使用自准直仪对曲面公式进行检验，将调整镜非线性程度大于2″的角度确定为需要分块的角度，观察其在采点平面的位置，确定需要分块的A/D 值；最后将曲面进行分块处理，以X轴传感器A/D 值进行划分，将非线性严重的X、Y正方向与X、Y负方向的大角度点去掉，使现在的曲面变成3 块曲面，即去掉大角度点的中心部分曲面，X、Y正方向曲面与X、Y负方向曲面3 个部分。

对X、Y正方向与X、Y负方向曲面进行更高密度的传感器采点与自准直仪数据记录，并进行曲面拟合。

在程序中，加入重新标定的大角度曲面公式，使它们分别作为相应位置的拟合曲面。在它们与中心部分结合的部分，选取X轴传感器A/D 值一小段使用加权方式进行计算，如此便可以解决调整镜非线性标定问题。

使用分段线性标定方法之后，分段区域共为5 块，共需要4 个分区值。分段区域分别为X和Y正方向大角度区域、加权区域1、中心区域、加权区域2、X和Y负方向大角度区域。程序流程图如图7所示。

图7 分段标定程序流程图Fig.7 Flow chart of piecewise calibration procedure

X轴分段标定程序伪代码如表1所示。

表1 程序伪代码Table 1 Program pseudo-code

程序中关键部分为加权部分的计算，程序以X轴A/D 值进行划分，使用if 函数分别对不同区域进行判断，使用曲面公式或两曲面公式加权的方式对角度值进行计算，最终返回角度值。Y轴同理。

X、Y正方向与X、Y负方向采点去除后，采点分布图如图8所示，曲面拟合图形如图9所示。

图8 分段后采点分布图Fig.8 Distribution of sampling points after subsection

图9所示为去除大角度点的拟合曲面与X、Y正方向和X、Y负方向的拟合曲面。可以看出拟合曲面覆盖住了所有的点，并且曲面整体较之前相比扭曲程度大幅减小。经过自准直仪的测试，调整镜±500″范围内非线性度误差小于2″。

图9 分段后曲面拟合图Fig.9 Surface fitting diagram after subsection

3 试验与结果分析

基于以上原理设计并制作了调整镜，如图10所示，并在相应实验环境中对其定点速度与线性度进行了检验。

图10 调整镜实验环境Fig.10 Experimental environment of adjusting mirror

1）速度

使调整镜以频率1 Hz 运行-500″～+500″的阶跃信号，示波器记录PSD 到位响应信号，响应时间小于3 s。

2）线性度

使用上位机控制调整镜运动到-500″～+500″范围内任意点，通过自准直仪观测镜面偏转角度，记录数据，数据如表2所示。

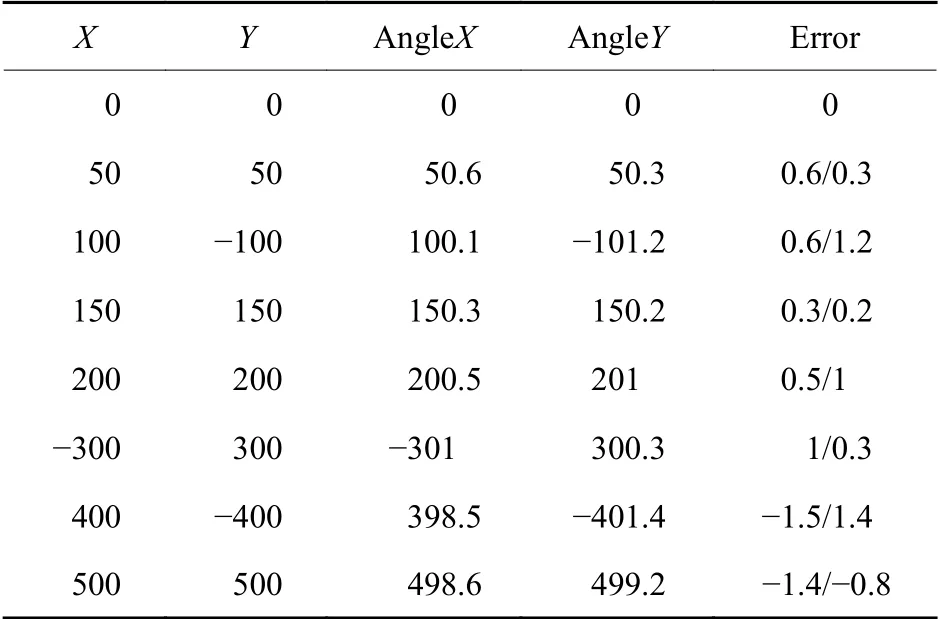
表2 调整镜线性度测试表Table 2 Linearity test of adjusting mirror(″)

根据表2 可知，调整镜的偏转误差均小于2″，调整镜的控制精度不受转动范围大小的影响。根据实验结果可以得出以下结论：调整镜在-500″～+500″范围内工作时，控制精度小于2″，可以满足项目要求的偏转速度与偏转精度。

4 结论

采用步进电机驱动的方式进行调整镜的设计，使用钢制一体化结构使调整镜具有良好的定点稳定性，并基于S 形加减速算法与分段线性的标定方法，使调整镜具有良好的偏转速度与线性度。到位调整相应速度小于3 s，偏转闭环重复定位精度小于2″，证明该系统可以达到较高的精度和速度。该系统能够较好地调整光束偏转方向，有效提高激光发射设备的激光发射精度。