基于三组元可调光焦度器件的变焦光学系统设计
2021-11-26程洪涛李恒宇
程洪涛,李恒宇
(1.上海健康医学院 发展规划处,上海 201318;2.上海大学 精密机械工程系,上海 200444)
引言
基于可调光焦度器件的变焦光学系统广泛应用在机器视觉、医疗和科学实验中[1-4]。可调光焦度器件的优点是给变焦系统设计提供了额外的自由度,不需移动光学器件,使系统结构更紧凑,极大提升了变焦光学系统的鲁棒性[5-7]。 目前,基于可调光焦度器件的变焦光学系统的研究主要集中在依据可调光焦度器件的调焦模型参数分析组元间的高斯光学参数,应用商业光学设计软件建立初始结构并优化[8-10],这些方法没有从几何光学理论上进行整体初始设计和研究,缺乏理论基础。
本文在近年来可调光焦度器件变焦系统的一阶和三阶研究理论基础上进行进一步拓展研究[11-13],提出了基于放大率的三组元可调光焦度器件变焦系统几何光学设计计算方法。其中分析了可调光焦度器件变焦的关键参数设计计算过程,得到了可调光焦度器件的控制方程,同时给出了三组元变焦物镜的设计实例,并与文献[14] 的基于三组元可调光焦度器件的分析进行比较验证,结果表明该方法完全可行。
1 三组元变焦系统光学设计原理
三组元折射系统是最典型的光学系统,应用在很多场合,三组元可调光焦度器件的变焦系统可等效成薄透镜,如图1所示。这种系统的倍率变化是以3 个实时的可变光焦度器件来实现的。透镜1、透镜2、透镜3 的光焦度分别为 φ1、 φ2、 φ3。组元的间距为d1、d2、d3、d4,共轭距为 Λ,系统放大率为m,系统倍率比为M=m2/m1,m2是最大放大率,m1是最小放大率 。假设d1、d2、d3、d4、m、M为已知。
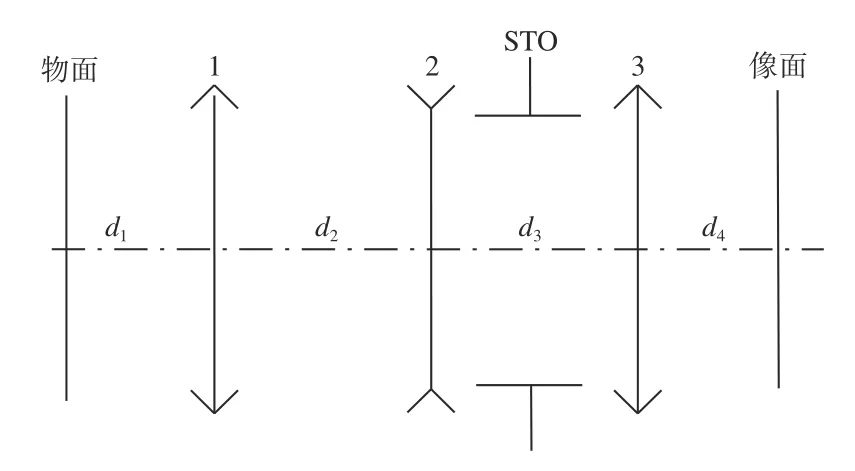
图1 三组元可调光焦度器件变焦系统等效薄透镜示意图Fig.1 Three-element equivalent thin lens zoom system based on variable focal power devices


2 三组元变焦系统初始参数计算
三组元变焦光学系统数据参数如表1所示。由于实际的可调焦系统有厚度,且变焦过程中透镜之间的距离会改变,在以下讨论和分析过程中,假定随着可调光焦度器件光焦度的改变,透镜间距基本保持不变,相对孔径大小保持不变,则变焦系统光学参数如表2所示。
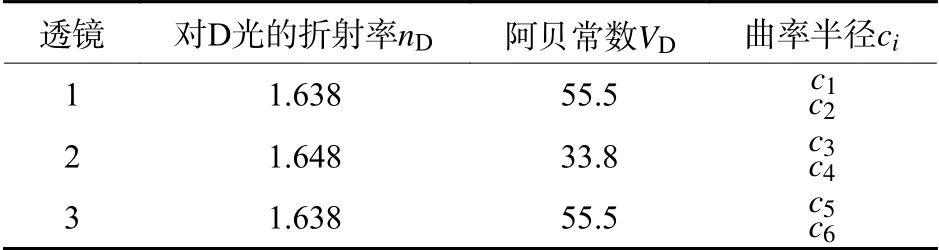
表1 可调光焦度器件参数Table 1 Parameters of variable focal power devices

表2 系统参数Table 2 System parameters
依据(9)式~(12)式可知,三组元变焦系统可调光焦度器件光焦度调焦方程为

(13)式~(16)式确定了透镜1、2、3 的光焦度控制方程和系统总的光焦度。需要进一步确定各器件的形状参数X的取值,同时考虑系统像差的复杂性和综合性,因此不考虑其他像差作为设计参考。以系统追求最小球差系数作为出发点,根据文献[12]中的公式:

得到以最小球差为优化参数时透镜1、2、3 的形状参数变化方程:
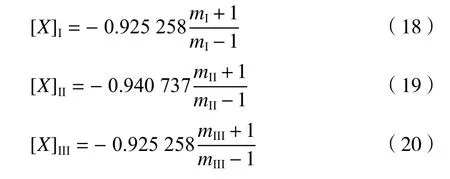
式中mI、mII、mIII分别为透镜1、2、3 的倍率值。针对该系统的成像质量,由于考虑到是薄透镜系统模型(简化的物理模型),因此本文采用光线追迹程序来完成三组元光焦度补偿变焦系统的像差评价。首先依据上面的探讨选取3 个位置的成像结果进行计算,分别是m=-0.05、m=-0.025、m=-0.01,根据(14)式~(16)式得到对应的各器件的放 大率一览表,如表3所示。

表3 系统放大率与变焦器件光焦度对应值Table 3 System magnification corresponds to focal power
根据薄透镜光学原理模型的光线追迹程序,代入表3 中透镜1、2、3 的光焦度值,同时应用(13)式得到三组元变焦系统的光焦度计算值,光焦度计算值和光线追迹值对比结果如表4所示。
从表4 中可以看出,计算值与光线追迹值相吻合(部分误差是因为光线追迹时小数点取6 位有舍入误差),说明公式(13)~(16)正确。

表4 光焦度计算值和光线追迹值对比Table 4 Comparison of focal power and ray tracing values
为进一步评估系统的光学性能,需要知道可调光焦度器件的曲率半径。(18)式~(20)式已经给出了可调光焦度器件的形状参数,根据曲率半径求解公式就可得到。计算公式如下:

根据(18)式~(22)式,可以得到在3 个不同放大率情况下各器件的不同曲率半径值。
m=-0.05
1)当时,各器件的曲率半径值如下:

?Xc0.191 433c10.047 092c2-0.031 959 0.533 793c3-0.364 148c40.110 685 0.525 336c50.376 812c6-0.117 259
2)当m=-0.025 时,各器件的曲率半径值如下:

Xc0.530 635c10.112 502c2-0.034 498 5 0.663 054c3-1.520 12c40.307 987 0.282 097c50.370 207c6-0.207 295
3)当m=-0.01 时,各器件的曲率半径值如下:

Xc0.612 388c10.149 478c2-0.035 934 0.803 405c3-5.463 306c40.595 573 0.214 103c50.370 919c6-0.240 098
将以上3 种情况下的数据输入到光线追迹软件中,波长取可见光(F、d、C),得到的像质评价结果如图2 和表5所示。

图2 不同放大率情况下的点列图Fig.2 Spot diagram with different magnification
从图2 可以看出,系统的像质质量在放大倍率数值较小时像质表现较好,放大倍率较大时像质表现较差。表5 给出不同放大倍率情况下的像差系数也说明了这种趋势,这符合变焦系统的特点,同时也表明了本文计算方法在小视场时更精确。

表5 不同放大率情况下的像差系数Table 5 Aberration coefficients with different magnification
3 归化对比验证
为了说明设计结果的有效性,并与文献[14]基于三组元可调光焦度器件的分析进行比较,对上面讨论的结果取放大率m值分别为-0.03、-0.025、-0.02,得到系统的变倍比为1.5。根据(13)式~(16)式得到不同放大率情况下的光焦度值如表6所示。根据(18)式~(20)式计算出本例在3 种变焦情况下的透镜形状参数,如表7所示。
对表6 进行缩放归化,得到的光焦度值如表8所示。从表8 可以看出,经过适当缩放后系统的焦距f′分别为1.2、1、0.8,与文献[14] 中表2 变焦系统总的焦距数据相同。下面比较本例和文献[14]的变焦系统的成像质量。
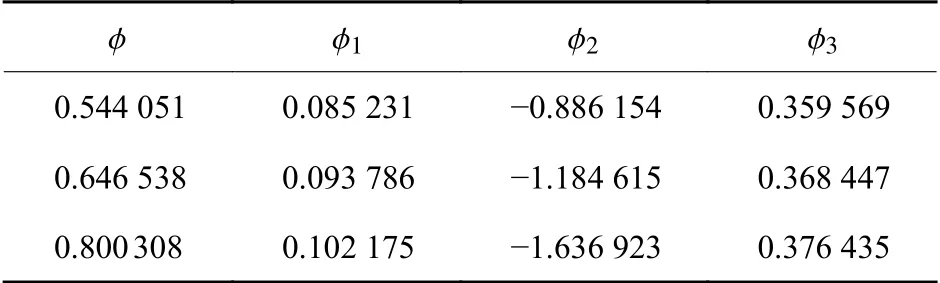
表6 不同放大率情况下的光焦度值Table 6 Focal power values with different magnification
首先,计算出本例在3 种变焦情况下透镜的曲率半径,依据表7、表8 和(21)式、(22)式得到三组元可调光焦度器件的曲率半径,如表9所示。
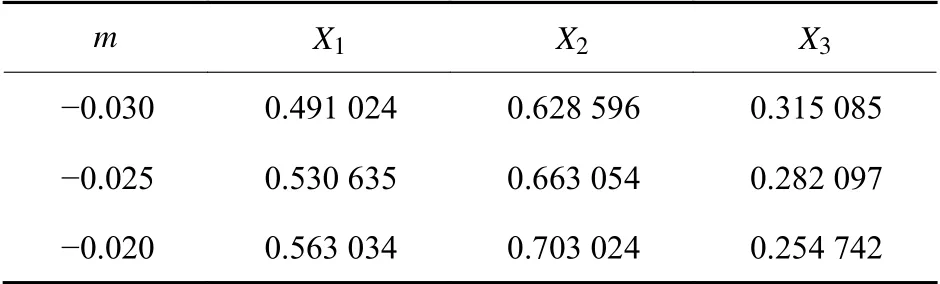
表7 不同放大率情况下形状参数值Table 7 Shape parameter values with different magnification

表8 归化后变焦器件的光焦度值Table 8 Focal power values after naturalization

表9 归化后光焦度器件曲率半径值Table 9 Radius of curvature after naturalization
其次,将表9 的数据输入到光线追迹软件中,该光线追迹软件是根据几何光学原理而特别设计的计算机程序,程序中应用了y-nu光线追踪原理,可以用来验证理论计算的结果是否正确。波长取可见光(F、d、C),得到的像质评价结果如图3所示。
根据文献[14]中表2 数据及其系统参数得到其点列图像质评价,如图4所示。

图4 文献[14]归化后不同焦距情况下的点列图Fig.4 Spot diagram of different focal lengths after naturalization in reference [14]
分析图3 与图4 可以看出,本例归化后不同焦距情况下的点列图整体表现要优于文献[14],说明在小视场范围内基于像差独立性原理以球差为最小优化值的求解是可信的。
4 结论
以薄透镜为可调光焦度器件的简化模型,探讨了基于三组元可调光焦度器件的变焦系统的初始设计理论。系统设计实例给出了系统长15 mm,相对孔径为1 /3的三组元可调光焦度变焦系统的初始控制方程,设计结果表明,系统结构简单、控制参数明确、变焦无轴向机械移动,可应用在光学内窥镜等狭小空间变焦的光学系统。
