环模制粒机齿轮减速器动力学特性分析

那日苏，贾开发，李 鑫，李 帅，张伟国

环模制粒机齿轮减速器动力学特性分析

那日苏1,2，贾开发1，李 鑫1，李 帅1，张伟国1

（1. 内蒙古工业大学机械工程学院，呼和浩特 010051；2. 内蒙古自治区液压传动与控制工程技术研究中心，呼和浩特 010051）

环模制粒机的内部激励会引起整机振动，振动是导致环模与压辊使用寿命降低的主要原因。该研究针对环模制粒机振动大、关键部件使用寿命短等问题，以SZLH420型环模制粒机减速器为研究对象进行动力学分析与试验。首先基于累积势能法计算齿轮时变啮合刚度，建立斜齿轮传动动力学模型，采用解析法对传动系统进行模态分析和非线性动力学求解，求得最大振幅向（水平径向）为0.008 mm、向（轴向）为0.004 2 mm、转角为0.000 87°，并通过有限元仿真验证动力学模型和固有频率。最后进行主轴扭矩测试与斜齿轮振动加速度试验。结果表明，整机振动加速度频率与斜齿轮一致，故斜齿轮传动系统对整机振动具有重要影响，其主要振动频率在4.25、9.17、13.86、18.13、23.86、47.53 Hz附近；齿轮振动最大幅值向为0.006 mm、向为0.004 mm，与动态响应计算对应振幅最大差值不超0.002 mm，验证了理论计算的准确性。研究结果可为环模制粒机性能的提高提供理论与试验依据。

振动；模态分析；斜齿轮；齿轮动力学；动态响应

0 引 言

环模制粒机（Ring Mold Granulator，RMG )是目前颗粒饲料生产的主要加工装备[1-2]。在生产过程中，制粒机振动会造成辊模磨损、环模使用寿命降低、可靠性差等问题，制约了颗粒饲料的推广使用。

斜齿轮减速器是制粒机的主要传动部件，齿轮啮合刚度与啮合误差的变化是造成传动系统振动的主要原因。国内外学者针对齿轮减速器动力学特性的研究主要集中在啮合刚度分析[3-4]、振动测试分析、模态分析及动态响应[5-7]分析等方面。Yang等[8-9]提出了正常和故障情况下齿轮时变刚度的计算方法，王峰等[10]开展了齿背接触特性的圆柱斜齿轮动态啮合刚度的研究，陈会涛等[11-14]研究了随机外部激励对齿轮传动系统动态特性的影响。

综上所述，目前的研究主要集中在外部激励对整机振动特性的影响，但针对传动系统内部激励引起的振动，导致关键零部件损坏、生产效率下降等问题鲜见报导。因此，本文以SZLH420型RGM为研究对象，采用势能法计算齿轮啮合时变刚度，建立六自由度斜齿轮系统动力学模型，求解RMG斜齿轮固有频率以及动态响应，并通过改变啮合刚度和啮合误差研究其动态响应，结合有限元分析和生产试验验证理论计算。分析齿轮减速器对整机动力学特性的影响，为传动系统计算分析和结构优化提供可靠依据。

1 环模制粒机结构及参数

该环模制粒机主要由驱动装置、传动装置、制粒装置等部分组成，其结构如图1所示，其主要性能参数如表1所示。制粒机空心轴经过抱箍带动环模转动，与和实心轴相连的双压辊形成相对转动，进而实现物料挤压成型。由于负载较大，故传动装置采用斜齿轮副传动。运转时，主电机通过联轴器与齿轮轴连接，从而驱动大齿轮带动空心轴回转，实现制粒。

表1 环模制粒机主要性能参数

2 RMG斜齿轮时变啮合刚度计算

为分析RMG齿轮传动系统的振动特性并进行动态响应计算，需进行斜齿轮传动啮合刚度的计算。斜齿轮传动具有平稳可靠的特点，将斜齿轮沿圆周展开（如图2所示），随着啮合位置的变化，齿轮上接触线长度循环往复变动，虽能够消除刚性冲击，但仍受柔性冲击的影响。

斜齿轮传动系统中，轴向振动、径向振动主要是由时变啮合刚度和啮合误差波动造成的。依据势能法，齿轮变形势能是由赫兹接触变形势能U、弯曲变形势能U、剪切变形势能U、轴向变形势能U组成。斜齿轮具有螺旋角，不能简单等效为悬臂梁结构。采用切片法，将斜齿轮沿着齿宽方向切成片，再用积分原理，将齿轮切片看作直齿相互刚性配合连接计算，即累积积分势能法。由累积积分势能法计算模型[4]，可得斜齿轮弯曲刚度k、剪切刚度k、轴向变形刚度k、基体弹性刚度k以及赫兹接触刚度k。则时变啮合刚度为

式中下标1和2分别代表主动斜齿轮和从动斜齿轮；代表齿轮同时啮合的齿数，表2为斜齿轮的基本参数。

表2 RMG斜齿轮减速器基本参数

将RMG减速器斜齿轮的基本参数依据势能法[4]进行计算，得多齿啮合时变刚度如图3所示。

在单一啮合周期进行曲线积分，除以啮合周期得曲线积分的平均值，即平均啮合刚度为K=5.2×108N/m，由图3可见，啮合刚度存在波动，则系统必然存在内部激励。

3 RMG斜齿轮动力学研究

3.1 RMG斜齿轮动力学分析

3.1.1 动力学模型分析

以420型RMG减速器斜齿轮传动系统为研究对象，输入轴和输出轴均为刚性轴，根据约束条件建立六自由度弯-扭-轴耦合动力学模型，如图4所示。不考虑摩擦的影响，依据牛顿第二定律建立RMG传动系统的动力学方程为

主动轮：

从动轮：

式（2）和（3）中，(=1,2)分别代表主、从动轮；m为质量，kg；y为切向位移，m；z为轴向位移，m；I为转动惯量，kg/m2；θ为转角位移，rad；T为斜齿轮的驱动力矩或负载力矩，N·m；F、F为系统的切向、轴向啮合力，N。

将制粒机斜齿轮减速器动力学方程（2）和（3）改写成矩阵形式为

式中为质量矩阵、为阻尼矩阵、为刚度矩阵、为广义系统外力矩阵。

3.1.2 RMG斜齿轮模态分析

为有效避免共振，应对齿轮系统进行模态分析[15-17]。模态分析时，阻尼和外力对系统的影响较小，可忽略。则斜齿轮动力学微分方程（4）可由下式表示：

由六自由度动力学模型确定该系统具有6个固有频率和6个主振型。设方程（5）解为=sinωt，即

3.1.3 RMG斜齿轮动态响应分析

具有时变刚度和啮合误差的动态系统啮合力分别为

式中r为分度圆半径，mm；k为平均啮合刚度，N/m；c为平均啮合阻尼，N/(m/s)。将上式带入动力学方程（2）和（3）中，考虑阻尼并对斜齿轮动力学微分方程进行求解[18]。RMG驱动电机的转速为1 480 r/min、负载扭矩2为3 700 N/m、综合啮合误差为()。综合啮合误差是由制造、装配误差所引起的，是齿轮振动不可忽视的重要因素，由式（10）计算得到。

式中f为基节误差，m；f为齿形误差，m。

经傅里叶级数变换，将时变啮合刚度（()）拟合为正态分布：

式中k为啮合刚度幅值，N/m。

平均啮合阻尼c为

式中为啮合阻尼比。

3.2 动力学计算与结果分析

3.2.1 动力学模型模态数值确定

根据制粒机斜齿轮参数，主动轮材料为优质碳素钢，密度为7.85 g/cm3，从动轮材料为可锻铸铁，密度为7.30 g/cm3。小齿轮采用齿轮轴，将轴的质量分配至节点，则主动齿轮轴的等效质量为

式中1为等效齿轮轴质量，kg；m为齿轮质量，kg；m为轴质量，kg。支撑轴为质量均匀分布的刚体，其转动惯量1为

式中为轴半径，mm；为材料密度，g/cm3。齿轮可以视为均质圆环，其内径是齿轮轴半径，外径是分度圆半径，则齿轮转动惯量2为

式中为分度圆半径，mm。轴承支撑刚度一般在107～108N/m，随着外部激励的变化在一定范围内波动。在不考虑波动的情况下，采用文献[21]中相关参数计算方法得动力学模型模态分析各项参数如表3所示。

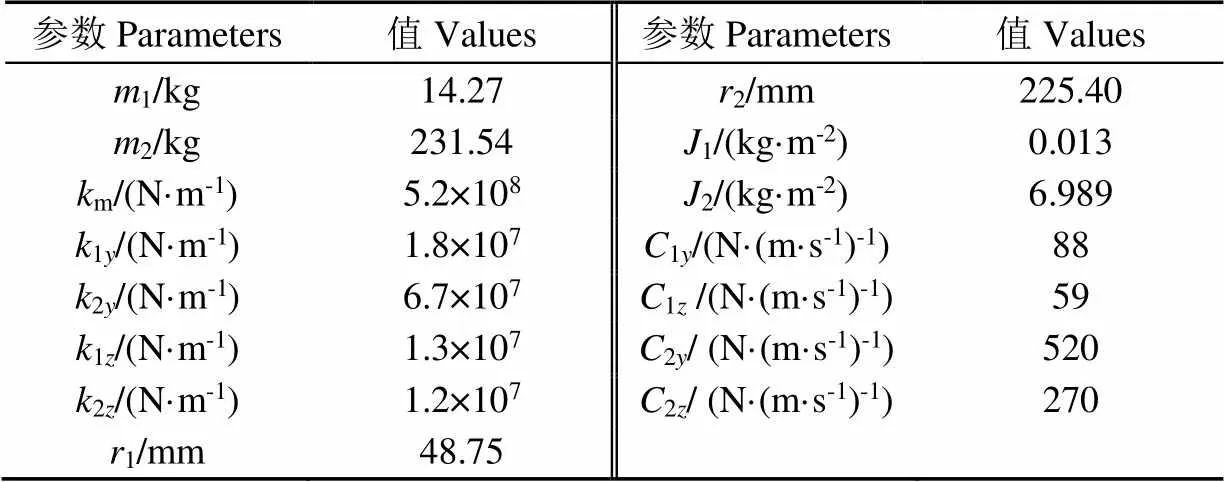
表3 动力学模型中的各项参数

3.2.2 RMG斜齿轮模态分析计算

将RMG斜齿轮模型参数带入模态分析计算式中，得其固有频率（表4）和主振型，其6个固有频率对应主振型分别为16：

向量(=1～6)分别代表6个自由度的最大位移。建立齿轮模型，将斜齿轮模型导入有限元仿真中进行模态分析[22-23]，结果如表4所示。

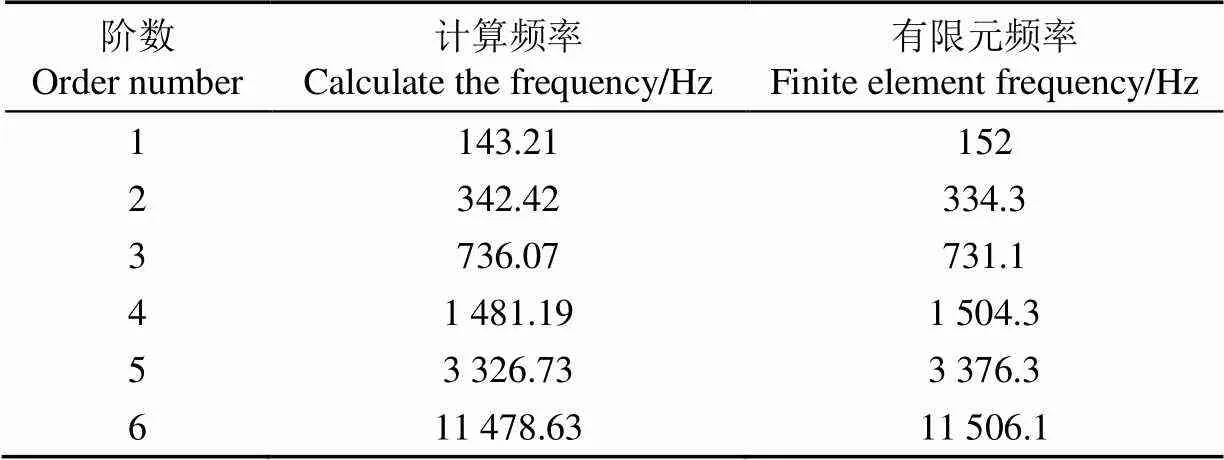
表4 RMG斜齿轮系统的固有频率

由表4得有限元频率与计算频率最大偏差为2.3%，两结果偏差较小，验证了动力学模型与理论计算的正确性。

3.2.3 RMG斜齿轮动态响应分析计算

应用Runge-Kutta方法进行非线性动力学微分方程求解，得斜齿轮传动系统动态响应，绘制各自由度的位移时域曲线，如图5所示。减小辐板开孔率、增加辐板厚度和轮圆厚度[24]以及齿面修形都会提升啮合刚度[25]，故将齿轮传动平均啮合刚度提高1倍，取k=1.04×109N/m，计算其动态响应，如图6所示。实际工作中，随着工作时间的增加，综合啮合误差将增大，故将其提高1倍，计算其动态响应如图7所示。

由图5可知，主动轮向最大位移约为0.008 2 mm，向最大位移约为0.004 2 mm，最大转角位移约为0.000 229°；从动轮向最大位移约为0.001 mm，向最大位移约为0.000 32 mm，最大转角位移约为0.000 87°；将转角位移转变为齿轮分度圆位移，约为0.01 mm，从动轮分度圆位移约为0.202 mm；得转角位移波动对系统振动影响最大、方向位移波动对其影响最小。由图6可知，当啮合刚度增大后，主动轮向位移减小0.000 5 mm，向位移减小0.000 1 mm，最大转角位移缩减0.000 086°；从动轮向位移缩减0.000 3 mm，向缩减0.000 07 mm，最大转角位移缩减0.000 3°。由图7可见：当啮合误差增大后，主动轮向位移增大0.000 4 mm，向最大位移增大0.003 3 mm，最大转角位移增大0.000 058°；从动轮向位移增大0.000 3 mm，向位移增大0.000 1 mm，转角位移增大0.001 3°。故应提高啮合刚度，降低啮合误差。

由计算式（8）和（9）可知，啮合误差和动态刚度具有较强的非线性且两种非线性相互叠加，造成系统响应出现周期或拟周期运动，增加了系统的冲击，令系统响应更加复杂，故出现图5～图7的波动曲线。依据机械手册，制粒机配合精度8级，要求向位移小于0.016 mm，向位移小于0.005 mm，未满足标准要求时将会造成产量和制粒质量的下降。由上述分析结果可知，相同条件下，增大齿轮啮合刚度，各振动幅值均有所下降；增大啮合误差，各振动幅值均有所增加。故采用减小辐板开孔率、增加辐板厚度、齿面修形、增加安装精度等方法均会优化系统动态响应。动态响应曲线波动复杂，与实际啮合过程中轮齿啮入、啮出、单齿与多齿交替啮合造成复杂响应的情况一致，故计算结果与生产实际情况相符。

图5 实际六自由度转角和位移

图6 增大啮合刚度转角和位移

图7 增大啮合波动误差转角和位移

4 RMG主轴扭矩和加速度振动测试试验

4.1 试验原理与设备

通过主轴扭矩试验研究主电机是否与传动系统发生共振，验证主电机是否为整机振动的主振源。通过振动试验验证齿轮传动的动态响应计算，并分析齿轮传动对整机振动的影响[26-27]。

以SZLH420型RMG为测试设备，采用北京必创有限公司TQ201H型无线扭矩测试节点、A302型无线加速度测试节点、BS951-T型无线网关、便携式电脑等进行试验，如图8所示。应用全桥测量方法测表面物理变形量，与半桥相比具有灵敏度高、测试结果更加准确的特点，同时可消除导线温度与弯曲应变压缩（拉伸）影响。将测试信号无线传输至节点，经计算机将动态信号分析处理，实现跟踪、记录。

为精准测量齿轮减速器的振动特性，将被测位置表面用砂纸擦拭打磨，使应变片与被测件严密贴合，避免变形量损失。分别选取代表性测点，对整机振动、斜齿轮振动以及主轴扭矩进行测量。

4.2 数据信号采集

4.2.1 主轴扭矩测试信号

将扭矩传感器安装至主轴测点，为保证测试波形准确性，多次更换主轴测点位置，取最具代表性的试验数据如图9所示。测得扭矩在710 N/m附近波动，其转矩符合主电机额定扭矩，其波动说明RMG载荷冲击较为严重。

4.2.2 整机振动试验

将振动传感器分别固定在RMG基座、箱体等测试位置进行振动测量试验[28-29]，通过对比启机、运转、停机以及各个测点的加速度采集数据，为比较整机两方向振动加速度，得整机向和向加速度曲线如图10所示。可见整机振动较为明显，向振动加速度高于向。

4.2.3 RMG齿轮传动振动试验

待RMG无进料且运行较为平顺，转速达到1 480 r/min的额定工况时，适合模拟只有主动齿轮与从动齿轮传动的工况，将无线加速度扭矩节点固定在靠近回转轴的支撑刚体上，得齿轮向和向加速度曲线如图 11所示。

4.3 结果与分析

4.3.1 频域曲线分析

为便于分析观察，将实测时域曲线图9～11经快速傅里叶变换，转换为频域曲线，如图12～14所示。

由图12可知，主轴扭矩的频域变化主要发生在1.5、4.78、24.46、25.1和25.43 Hz附近的频率。由斜齿轮系统的固有频率（表4）可知，斜齿轮固有频率较高，主电机不会与斜齿轮传动系统发生共振，为测量斜齿轮振动提供了前提条件。由图13可见，整机向加速度振动频域中，整机振动发生在4.25、9.17、13.86、18.13、23.86、47.53 Hz附近；向加速度振动频域中，整机振动发生在4.31、9.23、13.92、18.26、23.89、47.38 Hz附近。整机振动的向和向振动频率极为相近，但向幅值较大，其5阶频率23 Hz与电机激振频率24.46 Hz极其相近，可认为是主电机振动造成的。与图14对比可见，二者振动频率一致，说明齿轮是造成整机振动的重要原因。

图14 斜齿轮Y、Z方向加速度频域曲线

4.3.2 位移曲线分析

通过Bee Data软件分别对整机和斜齿轮、向加速度时域曲线图进行二次积分得到整机的、方向振动位移，如图15、16所示。

图15 整机Y、Z方向振动位移

由图15可见，整机向最大振动位移约为0.032 mm，向最大振动位移约为0.025 mm，向振幅高于向。由图16可见，主动轮向的最大位移约为0.006 mm，向的最大位移约为0.004 mm；从动轮向的最大位移约为0.003 mm，向的最大位移约为0.001 mm。齿轮振动主要发生在向，向振动较小。由于试验条件无法测定扭转位移振动，但根据理论计算结果可得扭转振动最大。齿轮传动的内部激励是构成整机振动、影响制粒效率以及制粒质量的重要因素。

图16 齿轮Y、Z方向上的位移曲线图

经动力学分析与试验结果分析可知：主动轮向位移偏差约为0.002 mm、向偏差为0；从动轮向位移偏差约为0.002 mm、向偏差约为0.000 63 mm，试验与计算结果最大偏差为0.002 mm，验证了理论计算的正确性与可靠性。齿轮传动内部激励引起的动态响应是造成整机振动重要原因。优化传动系统响应可通过增大啮合刚度和减小啮合误差等。具体可以通过减小辐板的开孔率、进行齿形优化、提高安装精度、进行定期保养等措施优化动态响应，进而避免由齿轮啮合引起的振动。

5 结 论

在RMG传动系统中，环模为易损件，振动是造成环模使用寿命降低的主要因素，研究系统内部激励对提高系统性能，降低颗粒饲料加工成本，具有重要的现实意义和实际应用价值。

1）采用累积势能法计算斜齿轮的时变啮合刚度，建立斜齿轮传动动力学模型，通过解析法求得斜齿轮传动的固有频率和动态响应，结果表明：分度圆位置扭转波动最大为0.202 mm，其次向0.008 mm、向0.004 2 mm；齿轮传动具有内部激励是引起振动重要原因，其动态响应具有周期性和拟周期性。

2）将啮合刚度提高1倍，动态响应波动下降0.000 5 mm，可以在一定程度上优化系统动态响应。随着工作时间增加，斜齿轮配合精度下降，轴承磨损增加，导致综合啮合误差增大，其动态响应波动呈非线性增加。故对齿轮系统进行维护、保养以及提高安装精度会有效避免振动。

3）由试验分析可得：主电机激振是引起整机振动的重要组成部分；主电机激振频率不会造成斜齿轮系统共振。理论计算与试验结果相符，验证了齿轮传动是引起制粒机振动的重要原因，为环模制粒机的结构优化提供了理论基础。

[1] 谭智，陆静. 饲料环模制粒机主体结构及工艺参数优化研究进展[J]. 饲料研究，2020，43(9)：118-120.

Tan Zhi, Lu Jing. Research progress on main structure and process parameters optimization of feed ring mold granulator[J]. Feed Research, 2020, 43(9): 118-120. (in Chinese with English abstract)

[2] 沈江飞，武凯，崔先岸，等. 转子偏心下环模制粒机的振动分析与结构优化[J]. 振动与冲击，2016，35(24)：59-65,95.

Shen Jiangfei, Wu Kai, Cui Xianan, et al. Vibration analysis and structural optimization of a ring die pellet mill with rotor eccentricity[J]. Journal of Vibration and Shock, 2016, 35(24): 59-65,95. (in Chinese with English abstract)

[3] 史丽晨，李坤，王海涛，等. 拖拉机行星齿轮箱故障响应特性动力学仿真及验证[J]. 农业工程学报，2018，34(7)：66-74.

Shi Lichen, Li Kun, Wang Haitao, et al. Fault response characteristics of tractor planetary gearbox based on dynamical simulation and its validation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 66-74. (in Chinese with English abstract)

[4] 魏鹏，邓松. 基于势能法的两级斜齿轮系统时变啮合刚度计算与动态特性研究[J]. 机械传动，2020，44(9)：51-57,71.

Wei Peng, Deng Song. Time-varying mesh stiffness calculation and research on dynamic characteristic of Two-stage helical gear system based on potential energy method[J]. Journal of Mechanical Transmission, 2020, 44(9): 51-57,71. (in Chinese with English abstract)

[5] 万志国，窦益华，张明泉，等. 齿轮系统动力学模型内部激励参数的优化设置研究[J]. 机械设计与制造，2021，(3)：101-105.

Wan Zhiguo, Dou Yihua, Zhang Mingquan, et al. The research on optimization settings of internal excitation parameters of gear system dynamic model[J]. Machinery Design & Manufacture, 2021(3): 101-105. (in Chinese with English abstract)

[6] 张建宇，李加军，杜晓钟，等. 内、外混合激励下风力机主传动系的扭振响应分析[J]. 机械设计与制造，2020，(8)：25-30.

Zhang Jianyu, Li Jiajun, Du Xiaozhong, et al. Analysis on torsional vibration response of main drive system of wind turbine under internal and external mixed excitation[J]. Machinery Design & Manufacture, 2020(8): 25-30. (in Chinese with English abstract)

[7] 林腾蛟，李润方，杨成云，等. 增速箱内部动态激励及系统振动响应数值仿真[J]. 农业机械学报，2002(6)：20-22，15.

Lin Tengjiao, Li Runfang, Yang Chengyun et al. Numerical simulation for inner dynamic excitation and system vibration response of speed increasing gearbox[J]. Transactions of the Chinese Society for Agricultural Machinery, 2002(6): 20-22, 15. (in Chinese with English abstract)

[8] Yang D C H, Lin J Y. Hertzian damping, tooth friction and bending elasticity in gear impact dynamics[J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1987, 109(2): 189-196.

[9] Liang X H, Zhang H S, Liu L B, et al. The influence of tooth pitting on the mesh stiffness of a pair of external spur gears[J]. Mechanism and Machine Theory, 2016, 106: 1-15

[10] 王峰，张健，徐兴，等. 融合齿背接触机理的圆柱斜齿轮振动特性分析与双面修形优化研究[J]. 振动与冲击，2018，37(24)：53-60.

Wang Feng, Zhang Jian, Xu Xing, et al. A study on vibration characteristics of a cylindrical spur gear with the contact mechanism of back teeth and optimization of double teeth surfaces modification[J]. Journal of Vibration and Shock, 2018, 37(24): 53-60. (in Chinese with English abstract)

[11] 陈会涛，吴晓铃，秦大同，等. 随机内外激励对齿轮系统动态特性的影响分析[J]. 中国机械工程，2013，24(4)：533-537.

Chen Huitao, Wu Xiaoling, Qin Datong, et al. Dynamic characteristics of gear transmission system subjected to random internal and external excitation[J]. China Mechanical Engineering, 2013, 24(4): 533-537. (in Chinese with English abstract)

[12] 刘大维，李国政，陈焕明，等. 车辆随机动载作用下路面动态响应研究[J]. 农业机械学报，2011，42(2)：28-33.

Liu Dawei, Li Guozheng, Chen Huanming, et al. Dynamic response of pavement based on random dynamic load of vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(2): 28-33. (in Chinese with English abstract)

[13] Zhou W G, Zhu R P, Liu W Z, et al. An improved dynamic transmission error model applied on coupling analysis of gear dynamics and elastohydrodynamic lubrication[J]. Journal of Tribol, 2022, 114(5): 51-60

[14] 秦大同，吕雪慧，陈锐博，等. 运行工况下风电传动系统机电耦合建模及其动态特性研究[J/OL]. 中国机械工程，1-9[2021-06-30]. http: //kns. cnki. net/kcms/detail/42. 1294. TH. 20210430. 1303. 010. html.

Qin Datong, Lv Xuehui, Chen Ruibo, et al. Electromechanical coupling modeling and dynamic characteristic analysis of wind turbine transmission system under operation conditions[J/OL]. China Mechanical Engineering, 1-9[2021-06-30]. http: //kns. cnki. net/kcms/detail/42. 1294. TH. 20210430. 1303. 010. html. (in Chinese with English abstract)

[15] Guo F Q, Du H M. Modal analysis of components and whole of gear pump[J]. IOP Conference Series: Earth and Environmental Science, 2021, 632(3): 1-15.

[16] 王冰. 齿轮传动系统传动轴模态仿真及振动实验测试研究[J]. 机械制造与自动化，2021，50(3)：110-112.

Wang Bing. Research on modal simulation of planetary gear transmission system frame and vibration experiment[J]. Machinery Building & Automation, 2021, 50(3): 110-112. (in Chinese with English abstract)

[17] 刘炀，周曼莉，孙飞杨. 基于Matlab和Workbench的变速器斜齿轮模态特性研究[J]. 现代机械，2019(3)：47-51.

Liu Yang, Zhou Manli, Sun Feiyang. Study on modal characteristics of transmission helical gear based on Matlab and Workbench[J]. Modern Machinery, 2019(3): 47-51. (in Chinese with English abstract)

[18] Han L, Qi H J. Dynamic response analysis of helical gear pair considering the interaction friction and mesh stiffness[J]. Journal of Theoretical and Applied Mechanics AIMETA, 2019, 54(5): 2325-2337.

[19] 钭奕轶. 斜齿轮传动系统的非线性动力学分析与研究[D]. 杭州：浙江理工大学，2019.

Dou Yizhi. Nonlinear Dynamics Analysis and Research of Helical Gear Transmission System[D]. Hangzhou：Zhejiang Sci-Tech University, 2019. (in Chinese with English abstract)

[20] 庞杰，韩振南. RV减速器传动系统动力学特性分析[J]. 机械设计与制造，2021(1)：147-151,155.

Pang Jie, Han Zhennan. Dynamic characteristics analysis of RV reducer transmission system[J]. Machinery Design & Manufacture, 2021(1): 147-151,155. (in Chinese with English abstract)

[21] 沙发明. 双离合变速器斜齿轮非线性动力学分析[D]. 合肥：合肥工业大学，2015.

Sha Faming. Study on Nonlinear Dynamic Characteristics of Helical Gear in Dual-clutch Transmission[D]. Hefei：Hefei University of Technology, 2015. (in Chinese with English abstract)

[22] 范舒阳. 斜齿轮动态接触理论及仿真研究[D]. 哈尔滨：哈尔滨工业大学，2020.

Fan Shuyang. Research on Dynamic Contact and Simulation of Helical Gear[D]. Harbin: Harbin Institute of Technology, 2020. (in Chinese with English abstract)

[23] 谢松成，杨荣松，周青华. 基于ANSYS Workbench的RV减速器随机振动分析[J]. 机械传动，2021，45(3)：111-116.

Xie Songcheng, Yang Rongsong, Zhou Qinghua. Random vibration analysis of RV reducer based on ANSYS Workbench[J]. Journal of Mechanical Transmission, 2021, 45(3): 111-116. (in Chinese with English abstract)

[24] 石慧荣，程艳霞，李宗刚，等. 机车辐板式直齿轮啮合刚度计算及传动优化[J]. 铁道学报，2021，43(1)：49-55.

Shi Huirong, Cheng Yanxia, Li Zonggang, et al. Meshing stiffness calculation and transmission optimization of webbed spur gears in locomotive[J]. Journal of the China Railway Society, 43(1): 49-55. (in Chinese with English abstract)

[25] 蒋进科，刘钊，彭先龙. Ease-Off修形准双曲面齿轮减振优化设计[J]. 华南理工大学学报：自然科学版，2020，48(5)：134-141,148.

Jiang Jinke, Liu Zhao, Peng Xianlong. PID position control of pneumatic muscle actuator based on RBF neural network[J]. Journal of South China University of Technology: Natural Science Edition, 2020, 48(5): 134-141,148. (in Chinese with English abstract)

[26] 耿令新，李康，庞靖，等. 基于时频和功率谱密度的移栽机振动特性测试与分析[J]. 农业工程学报，2021，37(11)：23-30.

Geng Lingxin, Li Kang, Pang Jing, et al. Test and analysis of vibration characteristics of transplanting machine based on time frequency and power spectral density[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(11): 23-30. (in Chinese with English abstract)

[27] 徐立章，李耀明，孙朋朋，等. 履带式全喂入水稻联合收获机振动测试与分析[J]. 农业工程学报，2014，30(8)：49-55.

Xu Lizhang, Li Yaoming, Sun Pengpeng, et al. Vibration measurement and analysis of tracked-whole feeding rice combine harvester[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(8): 49-55. (in Chinese with English abstract)

[28] 高珍，侯天柱，刘渊，等. 船舶齿轮箱振动测试分析及优化研究[J]. 推进技术，2020，41(11)：2587-2595.

Gao Zhen, Hou Tianzhu, Liu Yuan, et al. Vibration test analysis and optimization research of ship gearbox[J]. Journal of Propulsion Technology, 2020, 41(11): 2587-2595. (in Chinese with English abstract)

[29] 左曙光，刘敬芳，吴旭东，等. 车用离心风机转子系统振动特性分析[J]. 农业工程学报，2016，32(4)：84-90.

Zuo Shuguang, Liu Jingfang, Wu Xudong, et al. Analysis on vibration characteristics of vehicle centrifugal fan rotor system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(4): 84-90. (in Chinese with English abstract)

Dynamic characteristics analysis of the gear reducer of ring mold granulators

Na Risu1,2, Jia Kaifa1, Li Xin1, Li Shuai1, Zhang Weiguo1

(1.,,010051,;2.,,010051,)

Serious vibration in most mechanical equipment has posed a great impact on the production efficiency of agricultural goods and the service life of key parts. Many efforts have been made on the influence of external excitation on the vibration generation, transmission, and even reduction at present. However, there are only a few studies on the influence of internal excitation on vibration in the ring mold granulator, such as the ring mold and pressing roller. Taking the gear reducer of the 420 ring mold granulator as the research object, this study aims to analyze the dynamic characteristics of the complex transmission, large vibration, and short service life of key parts. The time-varying meshing stiffness and meshing error of helical gears were attributed to the internal excitation of transmission system. A cumulative integral potential energy was used to calculate the time-varying meshing stiffness of gear reducer in a ring mold granulator, thereby determineing the variation of meshing stiffness. Then, a six degree of freedom (DOF) dynamic model was established to determine some parameters for the helical gear transmission system in a ring mold granulator. Since the dynamic response clearly reflected the gear vibration, a modal analysis of transmission was made to effectively avoid the nonlinear dynamic resonance. At the same time, a systematic evaluation was carried out to explore the effects of meshing stiffness and comprehensive meshing error on the dynamic response of helical gear transmission. More importantly, the obtained meshing stiffness of helical gear was utilized to optimize the dynamic response of system for a higher installation accuracy in regular maintenance. Furthermore, a finite element (FE) software was used to verify the accuracy of natural frequency in the dynamic model. A spindle torque test of granulator was also carried out to measure the torque time-domain curve. Fourier transform (FT) was then utilized to transformed into the power spectrum curve. A spectrum analysis demonstrated that there was no resonance of main motor with the transmission system, although the complex internal excitation of a granulator from the torque fluctuation. Additionally, an acceleration vibration test was performed on the whole machine and helical gear transmission. The curve of vibration time domain was measured to transform into the vibration frequency domain. The vibration characteristics of helical gear transmission were analyzed to verify the internal excitation in the whole granulator. Finally, the curve of vibration time-domain was integrated to obtain the displacement fluctuation. The test and theoretical calculation of dynamic response indicated that the internal excitation was an important reason for the vibration of the whole machine.

vibration; modal analysis; helical gear; gear dynamics; dynamic response

那日苏，贾开发，李鑫，等. 环模制粒机齿轮减速器动力学特性分析[J]. 农业工程学报，2021，37(16)：15-23.doi：10.11975/j.issn.1002-6819.2021.16.003 http://www.tcsae.org

Na Risu, Jia Kaifa, Li Xin, et al. Dynamic characteristics analysis of the gear reducer of ring mold granulators[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(16): 15-23. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.16.003 http://www.tcsae.org

2021-06-30

2021-08-12

国家自然科学基金资助项目（52065050）

那日苏，博士，副教授，研究方向为机械系统动力学。Email：nrs3000@163.com

10.11975/j.issn.1002-6819.2021.16.003

TH132.4

A

1002-6819(2021)-16-0015-09