山地城市干线交通控制子区划分方法研究

谭景元，钟添翼，闫建华，蔡晓禹

(1.重庆市市政设计研究院, 重庆 400020；2.重庆市公安局交通巡逻警察总队，重庆 400055；3.重庆交通大学交通运输学院，重庆 400074)

山地城市干线的不均衡性对交通管控提出了新要求，单一固定的管控方法难以满足日益增长的交通需求。交通控制子区作为协调控制的重要单元，是指在对路网进行协调管控时，将交通特征相似的相邻节点或路段划分为同一控制区域，将交通特征差异性较大的节点或路段划分为不同的控制区域，以此将路网分为多个控制区域，针对不同控制区域实行适合该控制区域交通特性的管控方案，交通控制子区划分结果将直接影响管控方式及其实施效果。

Walinchus[1]首先提出交通控制子区的概念，建议将行政区划、路网条件、交通流特性等影响因素作为交通控制子区的划分依据。目前，交通控制子区研究集中在静态交通控制子区划分和动态交通控制子区划分方法。本文通过总结静态划分方法和动态划分方法领域中关联度指标计算与子区划分算法部分，分析山地城市干线多维不均衡性，提出相应算法思路和关键技术，并结合交通领域相关研究前沿，对未来交通控制子区划分方法领域发展方向进行展望。

1 现有交通控制子区划分方法

1.1 静态交通控制子区划分方法

静态交通控制子区划分研究主要通过分析不同影响因素，如道路几何条件、历史交通流参数等，对交通子区进行划分，当子区划分方案确定后，原则上不再进行改动。TRANSYT(定时式脱机操作交通信号控制系统)[2]与Robertson模型[3]是典型的运用静态子区划分方法的控制系统，结合路网条件、交通流量、信号控制方案等影响因素，实现了对控制子区最原始的静态划分。Stockfisch[4]提出了典型静态交通控制子区影响因素，包括交叉口间距、交通流特性、交通流离散程度和信号方案等。

Whitson等[5]和Chang[6]以及Synchro软件内的协调系数[7]明确了控制子区划分算法模型中关联度计算指标以及交叉口间合并阈值等关键技术，进一步量化了路网条件、交通流特征、信号控制方案等影响因素对子区划分的影响。静态控制子区划分方法大多依靠经验主观确定各因素对控制子区划分的影响程度。在前人研究基础上，别一鸣等[8]总结并提出了交通控制子区划分方法的3个重要原则：

(1)周期原则：交叉口信号周期差异性过大，一定程度上会影响交通状态的差异。因此，同一个子区内的信号周期建议保持一致。

(2)距离原则：交叉口间距是影响车队离散性的重要因素，故同一子区内相邻交叉口距离不能过大，否则车辆过于离散。

(3)流量原则：相邻交叉口间流量相似，表示交叉口交通状态相似，同时存在紧密联系，可以划入同一控制子区。

1.2 动态交通控制子区划分方法

1.2.1 关联度指标计算

关联度指标计算可以量化相邻节点划入同一交通控制子区的适宜程度，为子区划分奠定基础。Yagoda等[9]提出交叉口关联度概念和计算方法，建议将关联度>0.5的交叉口划为同一控制子区进行协调控制。Chang[10]充分考虑道路交通状态时变性和交通流离散性等动态交通因素，以交叉口合并阈值0.35，建立了交叉口关联度模型，实现了动态交通控制子区划分。Park[11]通过研究交叉口服务水平与各交叉口间的交通流量关系，提出了基于分布式车路协同的控制理论，并以分离阈值0和1，确定交叉口间的关联度,该阈值由专家经验法得出。高云峰[12]以下游交叉口排队长度为影响因素建立了最大流量与各路径总流量比的路径关联度指标。马万经等[13]综合交叉口间距、信号相位、排队和路径流量的不均衡性，建立了路径关联度模型指标。杨晓光等[14]和卢凯[15]建立了基于绿信比优化的相邻交叉口关联度计算模型，在提高过饱和路网通行能力的基础上进行控制子区划分。梁杰[16]和别一鸣等[8]结合国内交通状况，基于车队离散程度建立了量化模型，提出了分层控制子区划分思想策略，并在考虑周期差异性条件下提升了交叉口关联度计算精度，为交通控制子区划分提供依据。

1.2.2 子区划分算法

交通控制子区划分算法是在计算得到交叉口关联度的基础上，将各个交叉口划入不同控制子区。Moore等[17]提出了利用聚类方法，分析交叉口进口道流量比，进而划分子区，该方法相比最初仅用交叉口关联度划分的方法更加全面。Lin[18]建立了交通控制子区影响因素的定量模型和基于搜索算法的控制子区方法，实现了交通控制子区的全动态划分。Tian等[19]建立了基于启发式算法的交通控制子区划分方法，证明了3～5个交叉口组成1个协调控制子区时，协调控制效果最佳，实现了绿波带宽最大化。莫汉康等[20]基于诱导条件提出了控制子区的自动划分方法，基于距离、周期、流量三大划分原则分别建立了控制子区自动划分方法，提升了交通系统整体运行效率。李瑞敏等[21]基于协调程度系数对定周期的区域进行控制子区划分。段后利等[22]提出了基于超图模型的动态子区划分方法，在保证控制子区划分实时性的基础上能够有效对超大规模路网进行处理。陈宁宁[23]基于三大划分原则，以协调控制为目标，提出了一种基于关联度由大到小的路网搜索算法，建立了考虑交通流状态变化和控制效果的子区划分方法。卢凯等[24]采用遗传算法和降维算法快速优化控制子区，解决了在最优方案计算中维数过高的问题，实现了交通协调控制子区的快速动态划分。

1.3 现有研究评述

通过静态控制子区划分方法，可以简单快速得到子区划分方案，但由于对影响因素定量分析相对缺乏，难以量化影响因素对子区划分的影响程度。道路交通状态复杂多变，仅凭静态子区划分方法，难以获得最佳的子区划分方案。

动态控制子区划分方法利用实时交通流数据，根据道路交通状态的变化自动调整划分方案，使协调控制区域始终保持着最佳的子区划分状态。当前研究成果多为关联度指标计算与子区划分算法，在一定程度上为交通管控提供了支持。

动态控制子区划分中，关联度模型算法在科学性、客观性方面存在不足，过多依赖主观性的关联度阈值确定，缺少系统性理论支持，在实际交通问题中难以直接应用，亟须建立一种科学、客观、精准的交通控制子区划分方法。

2 山地城市干线多维不均衡性分析

2.1 道路标准条件

相较于平原城市地形平坦、规则，山地城市道路条件复杂多变，山川曲折，沟壑纵深，地形地貌均不规则。山地城市道路的修建受到复杂地形限制，城市往往被山水分隔，城市结构整体呈自由式组团分布，组团间联系不畅，需要靠大量桥梁隧道相连，瓶颈路段和立交节点不均衡。

重庆典型干线机场路，作为城市快速路，承担组团之间交通衔接，但由于地形条件等限制，道路标准不统一，干线车道标准不统一,造成路段瓶颈。山地城市道路瓶颈示意如图1所示。在桥隧路段连接处，车道数不统一会导致通行能力不同，饱和流量存在差异。机场路全线长26 km，穿越多个城市组团，共有9处立交桥，间距较小的仅为1 km，间距较大的超过3 km，且立交桥等级不一，如人和立交桥为等级较高的全互通立交桥，石盘河立交桥等级较低。道路位置条件标准不统一，则要求协调管控之前必须进行子区划分，划分结果将影响管控方案实施效果。

图1 山地城市道路瓶颈示意

2.2 交通运行状态

山地城市干线的交通运行状态在时空分布上存在较大差异性。机场路干线及沿线早高峰交通状态时空分布如图2所示。

(a)8：00

由图2可知，早晚高峰交通状态较拥堵，其余时间为缓行或者畅通；在道路条件较好、车道宽且车道数多、饱和度不高的路段，交通状态通常为畅通；在立交匝道交织区及桥隧连接处等瓶颈路段，交通状态通常呈现为拥堵；通常状况下，城市道路交通状态呈现为缓行。不同的交通状态应对应不同的管控措施，畅通状态，通常不会采取管控措施，多以情报板发布警示信息为主；缓行状态，通常进行诱导防止拥堵；拥堵状态，根据实际需要采用外围路网协调管控等方案。山地城市干线的交通状态分布通常较为复杂，且交通事故、施工占道等突发性因素会改变交通状态，单一固定的管控方式已不适合当前需求，交通现状对交通控制子区划分提出了更高要求。

2.3 出行需求分布

山地城市干线全线的交通出行需求并不均衡，城市地形和发展原因会导致某些区域、路段、节点承担大量交通出行需求。以重庆市内环快速路与学府大道相交的四公里立交桥为例，主城区由南向北交通出行必须途经四公里立交桥，此处承担南岸区、巴南区、九龙坡区由南向北方向的交通需求，导致四公里立交桥及周边的交通量巨大，常年处于拥堵状态，而内环快速路与学府大道其他路段，出行路径可替代，交通状态运行良好。

2.4 管控要求

山地城市干线全线重要程度存在差异，重要程度决定着管控要求。从人和立交桥至金渝立交桥方向，由于承载大量交通需求，机场路的重要程度和管控需求较高，某些路段管控需求相对较低。同时城市干线承担着警保卫等特殊任务，不同位置的管控措施也不相同。

相较于平原城市，山地城市的交通环境更为复杂，道路开口数量较多，通勤干线数量较少，桥隧瓶颈流量冲击性较大，交通控制子区划分难度将更大。因此，更加高效、精细化的交通协同管控十分必要。

3 面向实时调控的干线子区划分关键技术分析

以缓解山地城市实际交通问题为出发点，综合考虑山地城市地形地貌、交通特性，面向实时调控进行干线交通控制子区划分，即建立一套根据干线交通状态自动将干线划分为最适宜管控的若干控制子区的方法。技术路线如图3所示，主要分为数据库构建、节点关联度建模、干线子区划分和模型优化4个部分。

图3 技术路线

3.1 数据库构建

构建完备的数据库是后续开展节点关联度建模和干线子区划分的基础。数据库由交通静态数据和交通动态数据构成，交通静态数据主要描述干线道路结构，是干线道路结构组成的关键因素，同时对相邻节点间关联度产生重要影响，主要包含相邻立交节点间距、立交节点等级、路段车道数、车道宽度等；交通动态数据主要表征干线交通流特性，主要包含流量、速度、排队长度、行程时间、通行能力等。将上述数据清洗后，采用多源数据融合处理，包括不同数据格式的归一化、数据清洗筛选等，得到适用子区划分的交通参数，为后续研究工作奠定基础。

3.2 节点关联度建模

交通控制子区划分最终为协调管控服务，可以用干线路段、立交节点是否需要进行协调管控，来表示将其划入同一子区的必要程度，利用协调系数(coordinatability factor, CF)表示相邻节点间需要进行协调控制的必要程度[21]。CF值越大，表示节点越有必要进行协调控制，即越需要将相邻节点划入同一个交通控制子区；CF值越小，则表示没有越必要进行协调控制。考虑到山地城市道路标准条件、交通运行状态、出行需求分布和管控需求在整条干线上的不均衡性，本试验选取距离d、交通流量q、交通流构成o共3个影响因子，其影响系数分别为距离影响系数DF、交通流量影响系数QF和交通流构成影响系数OF，基于多影响因素权重法计算协调系数。

3.2.1 距离影响系数(DF)

山地城市干线存在多维不均衡性，相邻立交节点间距差异性突出，节点间距对协调控制影响显著，相邻节点间距小，一般认为节点间关联度大，需要进行协调控制，将其划入同一子区的必要性大；相邻节点间距大，车辆离散性会随之增大，导致车辆交通特征不稳定，协调控制必要性也较小。

利用距离影响系数DF表征节点间距对干线协调控制必要性的影响，计算公式见式(1)。

(1)

式中，d为相邻节点间距，m；dmin为最小关联间距，m，相邻节点间距小于最小关联间距时，距离影响系数DF为1，则相邻节点间进行协调控制必要性大，需要划入同一个交通控制子区；dmax为最大关联间距，m，相邻节点间距大于最大关联间距时，则距离影响系数DF为0，相邻节点间没必要进行协调控制，不需要划入同一个交通控制子区。

3.2.2 交通流量影响系数(QF)

山地城市干线主线承载交通流量较大，且差异性较小，但相交道路等级不一样，包括高速公路、快速路、主干路和次干路等，相交道路流量对干线流量存在冲击，流量越大，冲击越强。外部干扰较小时，干线适合进行协调控制；外部干扰较大时，干线协调控制必要性反而较低。利用交通流量影响系数QF表征相交道路流量对干线协调控制的必要性，计算公式见式(2)。

(2)

式中，q为相交道路流量，pcu/h；qmin为最小干扰流量，pcu/h，相交道路流量小于最小干扰流量时，则交通流量影响系数QF为1，节点进行协调控制必要性大；qmax为最大干扰流量，pcu/h，相交道路流量大于最大干扰流量时，则距离影响系数DF为0，相邻节点间没必要进行协调控制。

3.2.3 交通流构成影响系数(OF)

交通流构成影响系数OF表示通过连续节点车队中，非直行车辆数所占比例。直行通过下游节点的车辆数所占直行通过相邻上游节点车辆数的比例o表示协调控制的必要性，同时在一定程度上反映了干线车队的离散性，用交通流构成影响系数OF表示，计算公式见式(3)。

OF=1-o

(3)

式中，OF值越大，则表示干线协调控制的必要性越大，反之则必要性越小。

3.3 子区划分算法

利用多影响因素权重的计算方法，计算协调系数CF，计算公式见式(4)。

CF=α·DF+β·QF+γ·OF

(4)

式中，α、β、γ分别为DF、QF、OF的影响权重，根据实际路网情况而定。交通控制子区划分方案如表1所示。

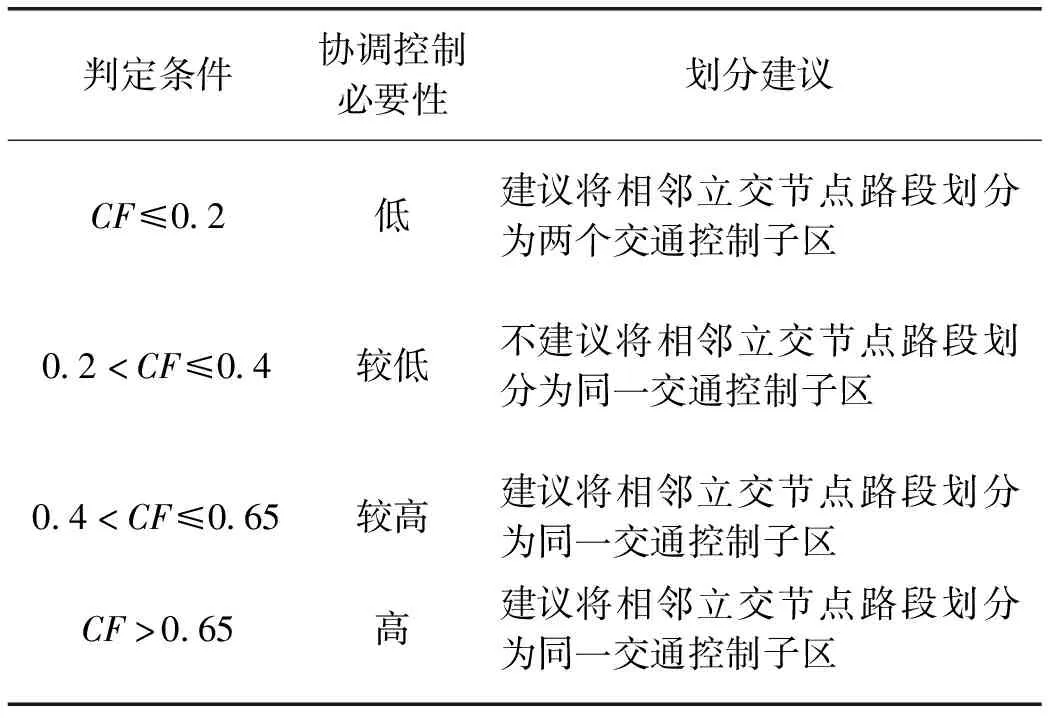
表1 交通控制子区划分方案

注：某个影响系数较大或较小可能会影响CF值，此类情况需要根据实际交通情况决定控制子区划分。

3.4 干线子区划分和模型优化

交通控制子区划分以利于交通协调控制方案的实施为目标，确定相邻节点是否为同一子区只是干线交通控制子区的初步划分，进而确定各交通控制子区的边界。车辆运行情况在干线可以用交通状态表征，交通状态一般分为畅通、缓行和拥堵。每一个控制子区都应该包含至少一个控制节点，优化节点关联度模型，以各节点的交通状态为依据调整子区边界，优化控制子区划分。控制子区划分方案的优劣最终需要根据管控的效果来检验，对管控后的干线交通状态进行评价，并采用反馈优化干线交通控制分区模型。

4 总结

交通控制子区划分方法已存在五十余年，从最初依照行政边界、道路几何条件、交通管理者经验等较主观、粗犷的静态划分方法，经过对节点关联度指标计算、子区划分算法的研究，发展到当前可根据交通实时状态的改变而改变的动态划分方法，建立了相对成熟的子区划分理论体系，更能满足当前精细化交通管控的需求。

交通控制子区划分结果将直接影响交通管控效果，传统的节点关联度阈值确定缺乏理论支持，无法避免子区划分结果带有主观性。本文通过分析山地城市干线的多维不均衡性，提出了面向实时调控的干线子区划分方法思路，为交通管理提供理论支持。山地城市交通环境复杂，以缓解实际交通问题为目标导向，基于交通大数据并配合交通管控系统，建立客观、准确的交通控制子区划分方法体系将成为未来研究重点。