一种单目无反射的头戴式三维视线跟踪系统
2021-11-24曹师好闫立兵秦贝贝张宝尚赵歆波
曹师好,闫立兵,秦贝贝,张宝尚,赵歆波,
(1.西北工业大学 计算机学院,西安 710129;2.陆装驻洛阳地区航空军事代表室,洛阳 471009;3.光电控制技术重点实验室,洛阳 471009)
0 引言
头戴式视线跟踪系统近年来已经成为市场研究、心理学研究[1]、人机交互[2-3]、智能教育[4]等领域被广泛使用的研究工具。最近,视线跟踪也被应用于虚拟现实和增强现实设备,用于控制[5]和全景渲染[6]。目前,市面上的头戴式眼动仪价格昂贵(例如,Tobii和Google Glasses)。因此,设计一套硬件结构简单、成本低的头戴式眼动跟踪系统对相关领域的研究有着很大意义。
当前,头戴式视线跟踪系统的方法可以分为二维和三维。二维的方法相对三维的方法在硬件结构要简单一些。二维的方法是将二维的眼动特征作为输入构建映射模型来获取人眼注视点位置,文献[7-8]利用一个相机和一个红外光源获取瞳孔中心和光斑形成瞳孔-角膜向量,通过多项式拟合来获取注视位置。该方法具有较好的准确性且硬件结构相对简单,因此成为头戴式的视线跟踪系统中最常见的方法。但这种方法在非标定点的精度并不理想。Arar等[9]利用固定的五个红外灯提取瞳孔中心以及四个光斑,根据几何学上的交比不变性原理获得注视点的位置。这种方法为了获取角膜光斑的反射位置需要较多的红外光源,使得硬件结构复杂,实用性较差。二维方法使用的二维特征并不能充分利用视线变换的信息,因此在非标定点精度较差。
与二维方法相比,三维方法根据眼球的结构特点,直接获取视线方向并计算与场景的交叉以估计注视点位置。但多数的三维方法依赖提前校准的测量信息:光源位置坐标、摄像机位置坐标、屏幕位置坐标等信息,对视线跟踪系统的使用造成了很大的不便。Shih等[10]利用两个相机和两个光源直接计算人眼光轴方向,避免了系统校准过程和校准误差。但此方法需要对多个相机进行标定且发光二极管的位置需预先设置。Roma等[11]通过将瞳孔和眼球半径视为已知量来构建三维眼球模型,将眼球中心到瞳孔中心的连线方向视为视线方向,此方法忽略了不同使用者之间的生理差异。满毅等[12]提出了一种基于双眼模型的三维视线估计方法,利用两个安装有红外灯组的摄像机组成立体视觉系统来获取双眼瞳孔坐标,并利用左右眼光轴与屏幕交点连线的中点做为注视点。但此方法在相机距人眼很近时,双眼数据容易丢失,所以在头戴式系统上的应用会有很大的限制。
综上所述,对于头戴式视线跟踪系统,现有的方法通常是使用瞳孔-角膜向量做插值的二维方法或者是使用三维眼球模型的三维方法。二维方法的问题在于瞳孔-角膜向量作为特征并不能充分利用视线变化的信息,造成在非标定上精度较差。三维方法的问题在于它通常需要对相机、红外光源的位置关系进行提前的校准或者是忽略个体差异对眼球进行统一建模,硬件结构复杂且制作成本高。目前还没有一种头戴式视线跟踪方法能在只有一个眼部相机且不使用眼球固定参数的情况下进行三维的视线估计。Swirski等[13]提出了一种单目的三维眼球重建方法,但是他们只是对仿真环境中合成的人眼图像进行了模型评估,从眼部相机到场景相机的映射精度的真实性能并没有被量化。因此,为了解决现有头戴式视线跟踪系统存在的问题,本文提出了一种头戴式单目无反射光斑的三维视线跟踪方法。与现有的方法相比,本文方法仅需要一个眼部相机,不使用眼睛的平均生理参数,且能够提高在非标点的精度。
本文的贡献主要有以下三个方面。首先,在分析Swirski[13]眼球模型的基础上,提出了一种计算眼球中心位置的优化算法;其次,优化眼球半径的算法并建立三维眼球模型,在此基础上重新计算瞳孔位置获取三维视线方向。最后,本文设计一套低成本、硬件结构简单的头戴式眼动跟踪系统,为相关领域的研究提供了很大便利。
1 三维眼球数学模型
1.1 眼球中心计算模型
Swirski等[13]提出的模型基于两个假设:①二维眼睛图像中的瞳孔椭圆轮廓是三维瞳孔圆P的透视投影,该圆形瞳孔中心与固定半径R的眼球相切;②眼球中心随着时间的推移相对相机是静止的。在他们的模型中,注视方向随着三维瞳孔圆P在眼球表面的运动而变化。在每一个时间点,眼球模型的状态由眼球中心c和三维瞳孔圆P来决定。
通过眼部相机在一段时间内收集到一组眼部图像,通过瞳孔检测算法[14]可以从每一张眼部图像中提取出瞳孔轮廓。Swirski等[13]通过迭代优化算法估计出眼球中心c和一组三维瞳孔Pi的参数(如位置和半径)。需要注意的是这种方法假设眼球中心在采集眼部图像时相对于眼部相机是静止的。

(1)
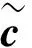
Swirski的模型在仿真环境下的合成图像上提取瞳孔轮廓边缘,然后根据这些边缘拟合的椭圆逆投影得到三维空间圆,并在此基础上估计眼球中心以及眼球半径,最后得到三维视线方向。该方法的局限性在于只在合成图像序列上进行了眼球模型的拟合,而实时视频中情况相比合成图像会更复杂。
在眼部相机拍摄的视频帧上进行瞳孔检测与在合成图像上进行瞳孔检测有以下两点区别。第一,合成图像上的瞳孔边缘都是清晰的,但在眼部相机的视频中,可能会出现运动模糊等现象。第二,合成图像的瞳孔的轮廓是完整的,此时拟合的椭圆的精确度要高。而眼部相机拍摄的视频帧,可能会遇到眨眼、睫毛遮挡或者眼球转动角度过大等情况。在这种情况下,瞳孔轮廓可能会被部分遮挡甚至完全遮挡,从而导致在视频帧上拟合的椭圆与瞳孔轮廓的误差较大。
在Swirski的模型中,为了消除圆的歧义性,通过将法向量投影到图像空间中,然后使用最小二乘法求解直线簇的交点做为眼球中心在图像空间中的投影。但此时是将所有瞳孔的法向量投影直线都计算在内,当遇到转动角度过大或者瞳孔轮廓不完整时,拟合出来的椭圆其法向量在图像空间的投影与眼球中心理论位置的投影的距离较大,如图1中的橙线和绿点。因此,本文提出优化算法来计算眼球中心c的位置。

图1 三维瞳孔圆的凝视向量相交
首先,通过逆投影可以从N个图像中计算得到N条直线,表示为LN,如式(2)。从中随机选取M条直线LM,此时公式(1)可改写为(3):
(2)
{M}=random({N})
(3)
(4)
(5)

1.2 三维眼球半径的计算
ni·(pi-c)>0
(6)
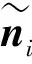
(7)

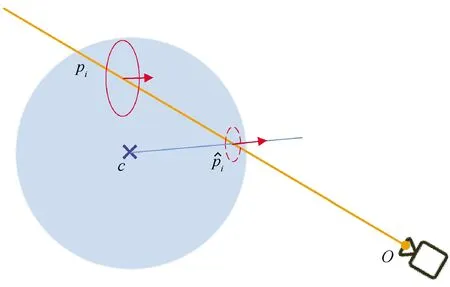
图2 瞳孔空间位置计算示意图
(8)
1.3 获取视线方向

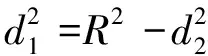
(9)
(10)
通过图3可以看出正常情况下,直线o-pi与眼球(c,R)会有两个交点,这里选择最近的交点。
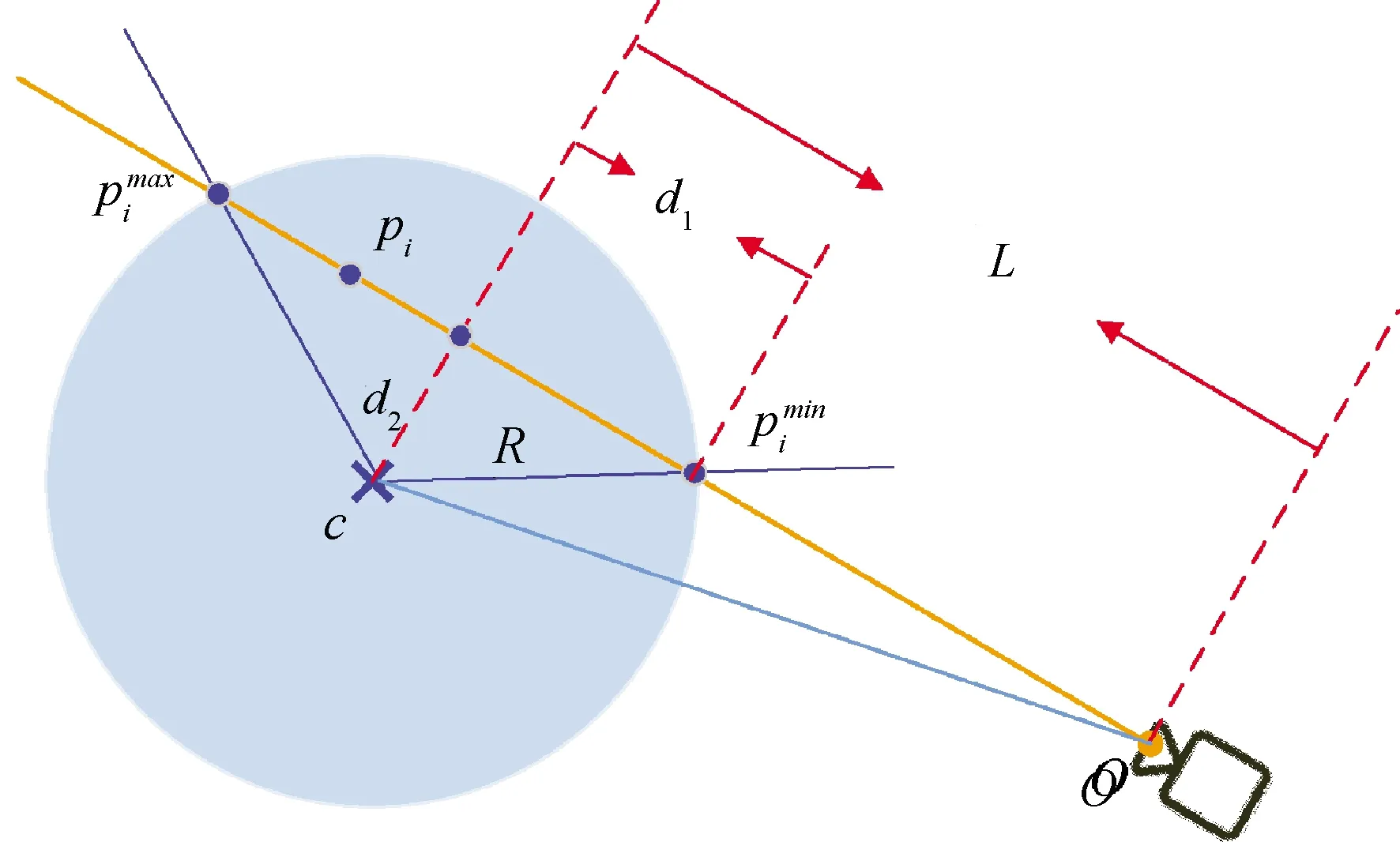
图3 瞳孔空间位置示意图
dmin=L-d1
(11)
(12)
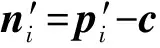
2 系统的设计和实现
2.1 系统设计
以第1节中眼球模型为基础,综合考虑头戴式眼动仪的需求。本文构建了一套使用单目相机的眼动跟踪系统,通过使用眼部相机收集眼部图像,检测出瞳孔轮廓的轨迹建立眼球模型。利用眼球模型获取视线方向,与标定点建立映射关系,得到注视点的位置。系统的算法流程如图4所示。

图4 系统算法流程图
2.2 系统实现
假设头戴设备相对头部保持固定,则设备上的近红外光源在角膜上形成的反射光斑位置固定,不随着眼球的转动而改变,故瞳孔角膜向量PCCR(Pupil center-corneal reflection)[21]只随瞳孔中心的变化而改变。然后通过插值公式将眼部相机图像中的瞳孔角膜向量(x,y)与场景图像或者屏幕上的像素点(X,Y)建立映射关系。
(13)
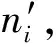
(14)
(15)
(16)
然后通过多项式建立注视方向角度(α,β)和二维平面坐标(X,Y)之间的映射模型。则(13)式可改写为:
(17)
从式(17)与式(13)的对比可以看出,本文设计的系统与传统瞳孔-角膜向量法使用的参数数量相同。本文提出的系统相对于瞳孔-角膜向量法,使用三维视线方向的角度去代替瞳孔-角膜向量,以此来提高对于视线信息变化的利用程度。使用三维到二维的映射模型来避免相机和头戴式设备间的提前标定,降低硬件结构的要求。
3 实验过程及结果
3.1 实验设备
本次实验使用实验室自制的头戴式眼动跟踪设备,其中场景相机、眼部红外相机的图像分辨率都为640×480 pixel,采集帧率为60 FPS。开发环境为Qt Creator 4.7+OpenCV 3.0。为了保证实验结果的公平性,本次实验使用相同的头戴式设备来测试PCCR方法和本文所提出方法的实验结果。
3.2 标定
在本次实验过程中,我们对本文方法和PCCR方法分别使用九点标定,然后各自注视标定点和非标定点并收集各自的注视点分布。其中标定过程使用的多项式为Cerrolaza等[16]提出的二阶多项式:
X=a0+a1x+a2x2+a3y+
a4y2+a5xy
(18)
Y=b0+b1x+b2x2+b3y+
b4y2+b5xy
(19)
在对本文方法进行标定前,我们要对眼球进行拟合。首先,要对眼睛图像进行收集,保持眼动仪对头部的相对位置不变,眼球转动1~2 s即可收集完毕。然后系统会利用第1、2节中的方法对视线角度进行计算,计算完成的结果如图5所示。

图5 眼球模型计算结果
其中,蓝点是眼球中心,红点是瞳孔中心,从蓝点开始穿过红点的绿色直线为视线。得到视线方向之后,根据公式(16),将方向转换为角度然后进行标定。
3.3 数据收集
测试者坐首先坐在屏幕前方0.7 m左右的位置,调整头部姿态保证屏幕上的所有标定点都在场景图像中出现,标定的过程中保持头部姿态固定,依次注视屏幕上的标记点,同时记录注视每个标定点时视线角度或者瞳孔-角膜向量。标定完成后测试人员注视标定靶上的一组点,每个点收集连续20帧的数据作为实验结果。剔除眼睛不自主地运动(如眼球震颤)等因素造成的显著偏移,本文所提出的方法和传统的PCCR方法注视标定点时在标靶上分布的可视化效果如图6和图7所示。
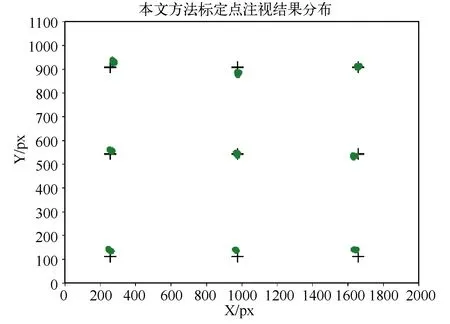
图6 本文方法注视标定点时结果分布图

图7 PCCR方法注视标定点时结果分布图
为了进一步对本文所提出的方法与PCCR方法在非标定点的精度进行评估,实验在标靶上固定了16个不同于标定点的测试点。本文方法和PCCR方法注视测试点时的视线分布结果如图8和图9所示。

图8 本文方法注视测试点时结果分布图

图9 PCCR方法注视测试点时结果分布图
其中,图6到图9中的十字代表标定靶上的标定点,点群代表实验中收集的真实注视点。在收集到注视点的数据后,利用式(25)来计算角度误差:
(20)
其中,N为合格的样本数量,(xij,yij)为收集的第i个注视点对应的第j个数据的位置,(Xi,Yi)为第i个参考注视点的位置。图10和图11给出了本文方法和PCCR方法在观察标定点和非标定点时每个点的角度误差。

图10 标定点结果

图11 测试点结果
根据图10和图11的实验数据可以得到,本文方法和PCCR方法在注视标定点时的平均误差分别为0.56°和0.60°,在注视非标定点时的平均误差分别为0.63°和0.94°。实验结果表明两种方法在标定点的误差接近,本文方法在非标定点上的精度得到了提升。从图9和图10可以看出,使用视线角度代替瞳孔-角膜向量作为特征能更充分利用视线变化的信息,整体提高系统的精度特别是在非标定点的精度。在仅使用单个相机且不使用眼球平均参数的条件下,本文方法相较于其他三维方法的精度并保持在同一水平。

表1 不同三维方法结果对比
4 结束语
根据瞳孔的运动轨迹特性,本文提出了一种单相机的头戴式三维眼动跟踪系统。通过分析瞳孔运动轨迹得到三维视线方向,降低了相机的数量。通过使用视线方向到场景的映射模型,避免了硬件结构的提前标定。而且结果表明,本文方法在使用相同的硬件设备时,相对于PCCR方法在非标定点上精度更好。在保证精度的同时,极大的降低了硬件结构的复杂度。当然,方法同样存在着标定过程繁琐的问题,这是因为本文想要验证本文方法相比PCCR方法在非标定点上效果更好。在实际应用的过程,可以通过使用Santini等[17]提出的CalibMe方法来简化标定过程,提高系统的实用性。
