基于遗传算法的铁路列车图像配准研究
2021-11-24赵歆波曹师好张宝尚
向 征,赵歆波,曹师好,张宝尚
(1.西北工业大学 软件学院,西安 710129;2.西北工业大学 计算机学院,西安 710129;3.光电控制技术重点实验室,洛阳 471009)
0 引言
近年来,铁路运输在世界范围内呈现高速发展的趋势。由于铁路运输存在一定的危险性,一旦列车存在潜在的安全风险,引起后果将不堪设想[1-3]。为了确保列车的行车安全,一系列保证列车行车安全的技术手段应运而生[4-5]。列车视频监控就是其中之一,如图1所示。列车视频监控借助于多个摄像头的协作拍摄,能够有效捕捉整个车身的实时视觉信息。但由于多个摄像头的镜头存在一定的拍摄误差,难以判断多个摄像头之间的差异和联系,借助人力判断费事、费力且存在较大的误差,易引起安全隐患[6]。因此,有效配准多个摄像头的信息,形成完整的列车图像,对于列车的安全监控是十分有意义的[7-8]。

图1 列车图像采集示意图
图像配准是一种解决摄像头信息整合问题的有效手段。图像配准(Image registration)即将不同时间、不同传感器(成像设备)或不同摄像条件下获取的两张及以上图像进行匹配,叠加的过程[9-10]。图像配准是许多应用问题的基本预处理步骤,如多源图像信息融合[11]。图像配准也被广泛应用于军事、医学、航空等多项重要科研领域。通过使用图像配准技术,我们能够获得质量更高、清晰度更好、信息更准确的图像信息。
对于不同类型的图像数据,配准方法也不相同。常见的图像配准方法分为两类:基于图像灰度的配准方法和基于图像特征的配准方法。基于灰度的配准方法直接利用图像的灰度信息,通过搜索方法确定使某种相似度取得最大或最小时的变换模型参数,该方法具有较大的精度和鲁棒性,但计算量较大,无法保证实时性。基于特征的匹配算法先提取图像的某种特征,然后对特征进行匹配,最后求变换模型参数并通过坐标变换完成配准,速度较快但精度不高。为了解决上述问题,我们尝试使用基于最大互信息的图像配准方法[12-14],即基于遗传算法优化的配准方法对列车图像进行配准[15]。遗传算法是一种模拟达尔文生物进化论中的自然选择机理和遗传学机理的计算模型,是通过模拟自然进化过程搜索问题最优解的方法[16]。遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。实验表明,基于最大互信息和遗传算法的图像配准算法能够准确、高效地完成图像配准任务。
1 研究背景
1.1 基于特征点匹配的图像配准
基于特征点匹配的图像配准算法需要经历特征提取、特征匹配、求解变换模型参数以及图像变换配准等步骤。具体流程如图2所示。其中,特征提取主要以SIFT,SURF特征为主,为了方便变换模型参数的求解,特征提取的数量需要满足一定的大小。同时,在求出待匹配图像的特征点后,特征之间需要进行相似度匹配,匹配过程首先是粗匹配过程,此过程会产生大量的误匹配对,随后是进行精匹配过程,进而剔除错误的匹配对。经历了特征匹配过程后,便可通过计算变换模型参数,然后对匹配图像进行空间变换,完成图像配准。

图2 基于特征点匹配的图像配准执行过程
SIFT点的特征提取需要大量的时间且匹配过程复杂度较高,因此存在实时性差的问题;同时,SIFT点特征提取方法对于较为光滑的物体特征提取能力有限,后期也会存在误匹配的问题。因此,为了解决如上问题,需要引入新的图像匹配算法。
1.2 基于互信息的图像配准
互信息作为一种相似性准则,描述了两幅图像的“相像”程度,互信息越大两幅图像越像,反之亦然。互信息最早被应用到医学图像的配准,取得了很好的效果。
互信息的定义为:
MI(A,B)=H(A)+H(B)-H(A,B)
(1)
式中,H(A)、H(B)分别为图像A、B的香农熵,H(A,B)为两个图像的联合熵。
基于互信息的图像配准就是要找到空间变换T0,使配准的两个图像的互信息达到最大,即:
T0= argmaxMI(A,T(B))
(2)
1.3 遗传算法
Holland于1975年首次提出遗传算法,该算法是模仿生物进化中的基因遗传和优胜劣汰等过程的一种仿生学优化搜索算法。遗传算法通过模拟一个人工种群进化过程,通过选择(Selection)、交叉(Crossover)以及变异(Mutation)等机制,不断迭代搜索出近似最优解,进而达到求解的目的。
遗传算法进行搜索时首先要对种群进行初始化,其中包括确定种群数量、确定迭代次数以及对染色体进行编码等步骤。算法需要确定问题求解的编码和解码过程,一般情况下采取实数编码或二进制编码,具体情况需要根据具体的问题求解进行设计。遗传算法的种群由种群数量个个体所组成,其中一个个体以一串变量特征描述,即基因描述,种群的初始化也就是初代种群根据规则生成的过程。
对于每一次迭代过程,遗传算法需要计算个体的适应度,也就是个体对于问题的匹配程度。适应度的值越大,解的质量就越高。
每一次迭代,种群需要经历选择、交叉、变异三个步骤。选择即从种群中选出适应性较好的个体,淘汰适应性较差的个体传入下一代种群。交叉即对个体对中的基因序列进行交换,通过交叉,遗传算法对解的搜索能力得到有效提高。变异即对个体基因序列中的基因值进行变动,变异操作使得遗传算法具有局部的随机搜索能力,并能够维持群体的多样性,防止算法出现过早收敛的情况。
在迭代次数或者种群中最优个体的适应度达到一定阈值后算法终止。种群中适应度最高的个体就是求得的相对最优解。
2 问题描述及方法
2.1 问题描述
列车图像配准的关键,就是使用具体的变换模型(例如,刚体变换,仿射变换等)将配准图像A在空间范围下进行线性变换,使其与参考图像B能够在位置上相匹配。计算机描述下的图像一般是堆叠的二维矩阵,设图像A与B在空间中的位置信息描述分别为I1(x,y)以及I2(x,y),其中x和y分别表示图像坐标系下的横纵坐标,则两个位置信息的关系可以表示为:
I1(x,y)=I2(f(x,y))
(3)
式中,f表示二维空间中的坐标变换方程。
2.2 遗传算法设计
遗传算法在解决特定问题的设计过程主要分为三部分:基因串的编码、适应度函数的设计以及终止条件的确定。
2.2.1 编码方法
为了有效表示水平、垂直偏移量以及旋转偏移量,并有效对解空间进行搜索,实验选择二进制编码表示配准的变换参数。如图3所示,其中ΔX表示水平方向偏移量,ΔY表示垂直方向偏移量,Θ表示旋转偏移量。

图3 基因编码方式
2.2.2 适应度函数设计
遗传算法的适应度主要用于评估个体对于环境的适应性。对于该算法,我们选择配准图像之间的互信息作为适应度函数,即:
F(t)=MI(A,B)
(4)
式中,MI(A,B)表示配准图像B和参考图像A之间的互信息。两张图片之间的互信息越大,配准的效果越好,个体的适应性越强。故我们将配准问题有效转化为多参数优化使F(t)达到最大的过程。如图4所示,使用互信息作为适应度函数,对同一摄像头捕获的不同时间的图像进行水平配准。
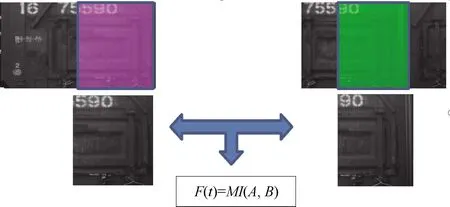
图4 基于互信息的图像配准
2.2.3 终止条件
遗传算法的终止可以通过固定迭代次数,或者根据种群个体信息进行判断。实验中我们通过固定迭代次数终止算法的执行。
2.3 算法执行过程
算法的大致流程如图5所示,其具体操作步骤细节如下:
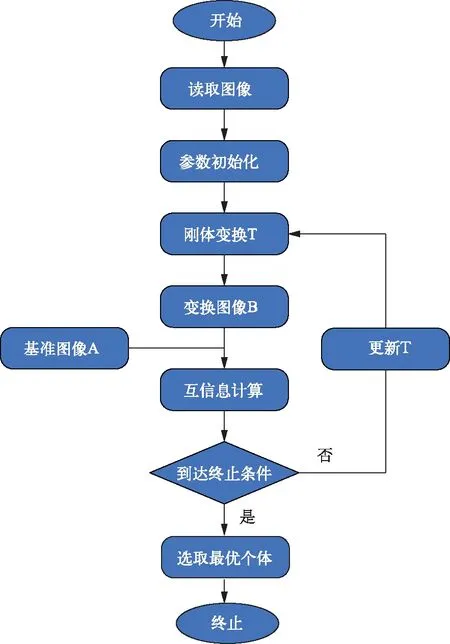
图5 基于遗传算法的图像配准求解过程
• 读取待配准图像A与B;
• 设置种群大小,种群数量过大,算法执行效率较低;种群数量过小,算法难以获得较优解,实验中我们设置种群大小为30;
• 对基因进行编码,初始化种群;
• 计算个体的适应度函数,实验中使用图片互信息作为适应度参数;
• 选择操作,选择操作的目的就是从当前种群中选择适应度较高的个体,并淘汰适应度较差的个体,实验中采用轮盘赌方法;
• 交叉操作,选择父代中的个体并对其基因序列进行部分交换,如果交换产生的子代适应度比父代更好,则替代父代个体,否则不进行替代;
• 变异操作,交叉操作后各种个体容易失去多样性,算法易整体落入局部最优,因此,需要对二进制位进行翻转操作以保证种群多样性,变异的概率我们设置为0.0.2;
• 反复进行选择、变异、交叉操作,直到达到算法迭代总次数。
3 实验及对比
为了体现遗传算法在解决图像配准问题上的优势,我们选择了数张按次序排列的配准列车图像进行实验,并以传统基于SIFT特征点的图像配准方法和基于模板匹配的方法进行比较[17-18]。实验主要硬件为i5 CPU,编程语言为C++。
3.1 算法对比
为了证明提出的方法的有效性,我们将本文提出的方法与基于特征点匹配的配准方法和基于模板匹配的配准方法进行处理时间对比。经过反复人工测量,实际水平偏移量为338像素。

表1 不同算法时间效率对比
实验结果表明,基于特征点匹配的配准方法使用SIFT算法提取特征进行特征匹配,最终计算变换参数。在特征提取与特征匹配过程会花费大量时间,因此所需的时间较长,但像素误差较低。基于模板匹配的配准方法不需要特征提取的过程,因此时间效率上优于基于特征点匹配的方法,但仍然需要遍历所有的搜索空间,获取最优解。我们提出的算法,省略了全局搜索与特征提取的过程,所以时间效率更优且像素误差更小。
相比于基于特征点匹配的配准方法,我们的算法也具有空间效率的优越性。基于特征点匹配的配准方法需要同时加载基准图像和目标图像。图像质量越高,图像越大,其提取的特征点更加稳定,但是需要耗费更大的空间资源。基于模板匹配的配准方法与我们提出的算法所需空间资源大小接近,但本文方法的时效性更优。
3.2 算法鲁棒性分析
通过调整算法参数并在多张图片上进行实验分析,实验的结果为多次运算取平均值。传统基于SIFT特征点的图像配准计算的偏移量为339像素。我们使用不同的迭代次数以及种群数量进行了10次试验,使用遗传算法对水平方向的偏移量进行求解。计算结果如表2所示。

表2 遗传算法最优解偏移量
实验结果表明,在迭代次数较少且种群数量较小的情况下,算法的稳定性略低且解的偏移存在误差;随着迭代次数与种群数量的逐渐增加,算法能够逐渐稳定并趋紧较优解,由表2明显可知最优解的标准差逐渐减小。
3.3 算法性能比较
对于传统算法,由于其需要经历较为费时的特征点提取、特征点匹配以及特征点筛选步骤,如果减少这些步骤的复杂度则算法的质量将无法保证。对于遗传算法,由于其具有较强的全局搜索能力,通过调整算法超参数,算法能够在较短时间内获得可行解。在不同条件下的系统耗费的运算时间如表3所示。
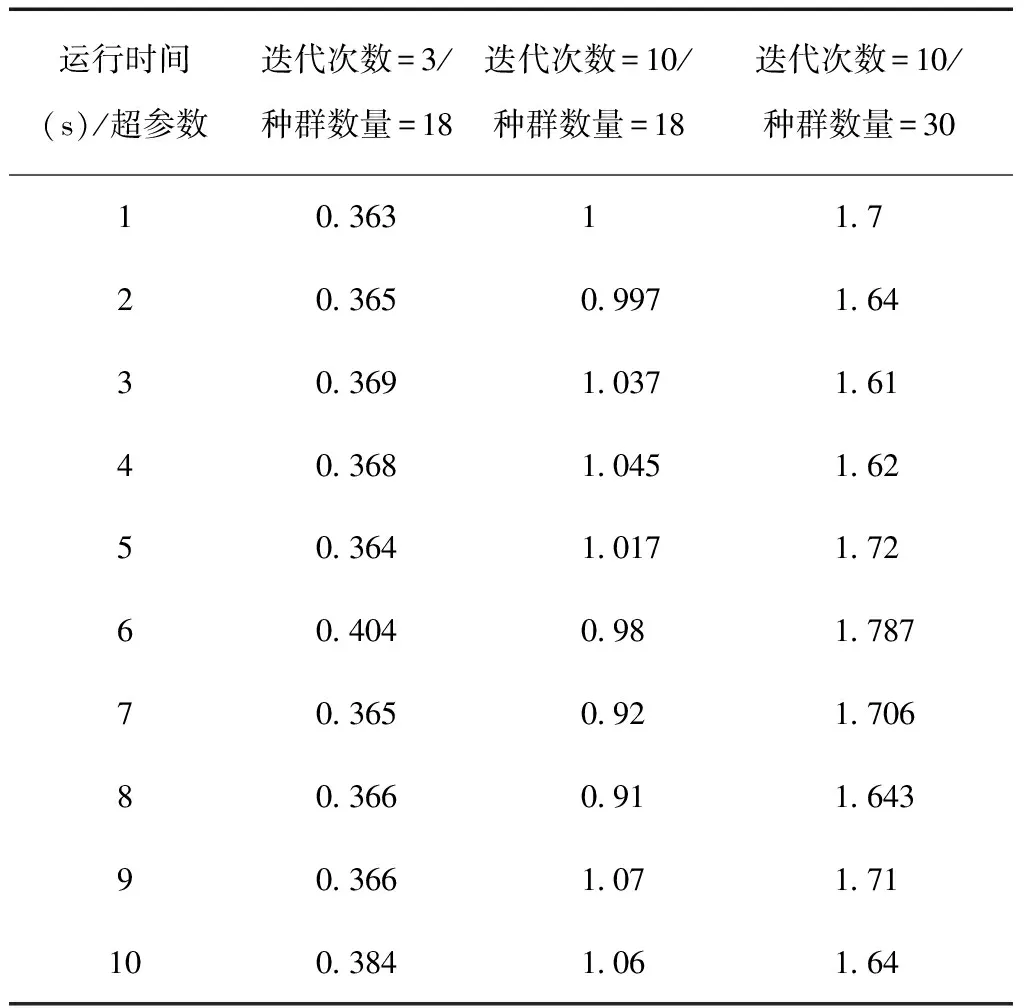
表3 遗传算法运行时间
由表3可知,在种群数量以及迭代次数较少的情况下,算法的运行时间较短,但解的质量较低;当算法的迭代次数以及种群数量较大的情况下,尽管解的质量较高但运行的时间有明显上升。通过对算法参数调整,在迭代次数为10,种群数量为18的情况下,算法的求解效率能够达到接近1秒/次匹配。
同时,对比传统的特征点算法,在获得相对稳定的偏移量解的情况下,需要的时间接近4 s,遗传算法在该情形下的求解能力明显优于传统方法,更加适用于实时列车图像匹配。
3.4 实验效果
为了更进一步说明本文算法的有效性,我们对比了列车图像配准前后的效果。图6表示单一摄像头采集的列车图像序列;图7表示使用本文提出的算法进行配准并完成拼接的列车图像。实验效果表明,我们的算法适用于铁路列车图像配准任务。

图6 采集的列车图像序列

图7 配准拼接后的列车图像
4 结论
本文提出了使用遗传算法解决图像配准问题的算法,实验表明,算法能够有效地校正多摄像头拍摄造成的偏移,并且具有较好的稳定性和效率,具有较强的实际使用价值。
