一种适用于单胎动物多品种选择的基因组关系矩阵

张洪志，任端阳，安丽霞，乔利英，刘文忠

(山西农业大学动物科学学院，太谷030801)

最佳线性无偏预测(best linear unbiased prediction, BLUP)使用系谱信息构建分子血缘相关矩阵(A阵)，结合表型信息计算常规估计育种值(estimated breeding value, EBV)[1]。对于易测量、中高遗传力的性状，BLUP取得了较好的应用效果[2-3]；但是对于低遗传力性状、限性性状、难以测定及生命晚期才能测定的性状等，其应用效果较差[4-5]。

单核苷酸多态性(single nucleotide polymorphism, SNP)芯片可提供生物个体全基因组范围的基因型信息。随着SNP芯片技术的发展及其制作成本的降低[6]，SNP芯片正被广泛应用于基因组选择(genomic selection, GS)[7-8]。GS是一种全基因组范围的标记辅助选择[9]，用来计算畜禽个体的基因组估计育种值(genomic estimated breeding value, GEBV)。最初实施GS使用“多步”法[10]，包括基因组最佳线性无偏预测(genomic BLUP, GBLUP)和贝叶斯及其改进方法[11-12]。多步法使用EBV[13]或逆回归育种值[14-15]作为伪表型值，通过伪表型值和基因组信息预测GEBV，从而用于选种[16]。由于使用伪表型值及一些参数估值有偏，多步法的可靠性较低[17]。一步法(single-step GBLUP, ssGBLUP)将基因组信息添加到由系谱信息构建的A阵中构建基因组关系矩阵(H阵)，结合表型信息直接预测未基因分型个体的EBV及基因分型个体的GEBV。ssGBLUP的计算步骤较简单且准确性不比多步法低[17-18]，已在奶牛育种中广泛应用[19-20]，这得益于在奶牛中可以组建足够规模的参考群体[21]。

对于肉牛、绵羊等家畜，通常群体规模较小，实施单品种GS(within-breed GS, wbGS)效果较差[22]。针对这一科学问题，提出并逐渐开始研究多品种GS(across-breeds GS, abGS)[23-24]。但是，目前缺少针对abGS的统计方法，使得abGS的应用效果较差[25]。

本研究旨在提出一种针对abGS的基因组关系矩阵构建方法，并通过模拟研究对该方法的使用效果进行评估，为abGS的实际应用提供新思路。

1 材料与方法

1.1 数据模拟

1.1.1 群体结构 使用QMsim软件[26]模拟数据。模拟4个数量性状基因座(quantitative trait loci, QTL)数水平(50、100、500、1 000)及3个遗传力(heritability,h2)水平(0.1、0.3、0.5)，共产生12个 性状。模拟牛的29对常染色体的50K SNP标记信息。对整个模拟过程重复10次，以减少抽样误差。模拟的群体结构和基因组参数见表1和表2。

表1 群体结构模拟参数

表2 基因组模拟参数

第一步，模拟历史群体。起始群体规模为3 000头，至500代时，群体规模递增到40 000头，至800代时，群体规模递减到30 000头，以得到与实际肉牛群体相似的连锁不平衡(linkage disequilibrium, LD)程度和突变-漂变平衡[27]。整个历史群体创建阶段，公母数目保持一致，采用随机交配。

第二步，模拟5个当代群体，每个群体模拟13个世代，视为5个品种。5个当代群体相互独立，分别从历史群体最后一代随机选择10头公牛，100头母牛作为当代群体的初始群体。模拟群体的前9代作为扩繁群体，公牛的淘汰率为60%，公、母牛的增长率为35%；10～13代公、母牛淘汰率分别为60%和20%，公母牛数量不再增长。公、母牛随机交配，每头母牛每年生产1头后裔，公、母后裔各半。选择估计育种值(estimated breeding value, EBV)高的个体留种。

使用Henderson动物模型[28]BLUP估计EBV。模拟性状表型方差标准化为1，个体的真实育种值为所有QTL加性遗传效应之和，个体的表型值为真实育种值与随机残差之和。模拟数据不考虑固定效应。

1.1.2 基因组 基于牛的真实基因组信息[29-30]，模拟29对常染色体，总长2 333 cM。为了模拟接近真实情况的SNP-QTL的LD，依据真实染色体长度及数目模拟基因组信息。模拟50 000个SNPs标记，假定SNP标记均匀分布在全基因组范围内，标记无效应。对QTL数设(50、100、500、1 000)4个水平，QTL的最小等位基因频率(minor allele frequency, MAF)为0.1。假定QTL在全基因组范围内随机分布，QTL效应值服从伽马分布(形状参数为0.4)。为了创建突变-漂变平衡，设置历史群体中QTL和SNP标记的回复突变率为10-5。

1.1.3 参考群体和候选群体 选择5个品种的第8～12代个体作为联合参考群体，5个品种的第13代作为联合候选群体。5个群体中挑选10～12代 有后裔的个体保留基因型信息，第13代随机选择250个个体(每个品种50个)保留基因型信息。对于基因分型个体，对其模拟不同比例(20%、40%、60%、100%)的系谱缺失，即个体的父号或母号未知。之前大部分GS的模拟研究只将无表型有基因分型的个体作为候选群体，Christensen用真实数据进行交叉验证发现[31]，ssGBLUP模型对候选群体中基因分型和未进行分型的个体均能提高GEBV的准确性，在GS实施阶段，可以对部分候选群体进行基因分型就能整体提高GEBV的准确性。本研究只对部分候选群体进行基因分型，更有实践意义。

1.2 统计模型

使用ssGBLUP模型：

y=Xb+Zu+e

其中，y为表型值向量；b为固定效应向量；u为育种值向量；e为随机残差效应向量。X和Z分别为固定效应和育种值向量的关联矩阵。

混合模型方程组为：

H阵为：

H=

H阵的逆表示为：

其中，Gw=(1-w)G+wA22，A阵为基于系谱构建的分子血缘相关矩阵，A22阵为基因分型个体对应的分子血缘相关矩阵，G为利用标记信息构建的基因组关系矩阵，w为对A22的加权系数，本研究中，w取值0和0.05(其中：newGw=0.95newG+0.05A22，Gw=0.95G+0.05A22)。使用两种G阵构建H阵：

(1)常规/标准G阵：

(2)新型G阵(newG)：

其中，M阵的维度为m行n列，m为基因分型个体数，n为标记数。标记位点基因型用(0，1，2)表示，0和2代表两种纯合基因型，1代表杂合基因型。P阵中的元素为标记的第二等位基因频率，Q阵的元素为标记的第二纯合基因型频率，pj为第j个标记的第二等位基因频率。

对于联合群体中符合哈代-温伯格平衡(Hardy-Weinberg equilibrium, HWE)的位点，若Q0为该位点的第二纯合基因型频率，p0为第二等位基因频率，则：

对于联合群体的非HWE(Hardy-Weinberg disequilibrium, HWDE)位点，若Q1为第二纯合基因型频率，p1为第二等位基因频率，则：

1.3 GEBV的预测准确性

使用Gmatrix软件[32]构建常规G阵，使用R语言自编程序构建新型G阵，使用DMU软件[33]计算GEBV。

在不同h2、QTL数及基因分型个体系谱不同缺失比例下，通过候选群体GEBV与真实育种值(true breeding value, TBV)的相关性(correlation coefficient,cor)来衡量应用不同G阵的预测准确性：

其中，Cov为协方差(covariance)，Var为方差(variance)。

2 结 果

2.1 参考群体和候选群体

本研究模拟了从相同的历史群体得到的5个独立的当代群体(品种)，群体结构模拟结果见表3。使用5个品种的第8～12代作为联合参考群体，个体数为31 935，其中10～12代中共有5 865个个体有基因型信息。将5个群体的第13代作为联合候选群体。候选群体共有7 445个个体，共有250个个体有基因型信息。

表3 模拟数据的当代群体结构

2.2 基因分型个体系谱无缺失时各模型的预测准确性

基因分型个体系谱无缺失时，QTL数和h2变化时各模型的预测准确性见表4。可见，QTL数为50，h2为0.3和0.5，及QTL数为100、500和1 000，各种h2时，newGw阵和Gw阵准确性相同，且较newG阵高0.0%～0.2%。QTL数为50，h2为0.1时，newG阵较newGw阵和Gw阵准确性高0.1%。在各QTL数及h2情况下，G阵准确性最低。

表4 基因分型个体系谱无缺失时不同QTL数和遗传力下各模型的预测准确性(10次重复的均值)

2.3 基因分型个体系谱部分缺失时各模型的预测准确性

基因分型个体系谱不同比例缺失(20%、40%、60%)时，QTL数和h2变化时各模型的预测准确性见表5。可见，各QTL数和h2情况下，newG阵的准确性最高，newGw阵与Gw阵准确性有略微差异(-0.4%～0.3%)，G阵准确性最低。随着基因分型个体系谱缺失比例增加，在各QTL数及h2情况下，除G阵外，其他3种G阵准确性逐渐下降，相对于newG阵，newGw阵和Gw阵准确性降低幅度较大。系谱缺失对G阵无明显影响，随着缺失比例增加，G阵准确性甚至会增加。

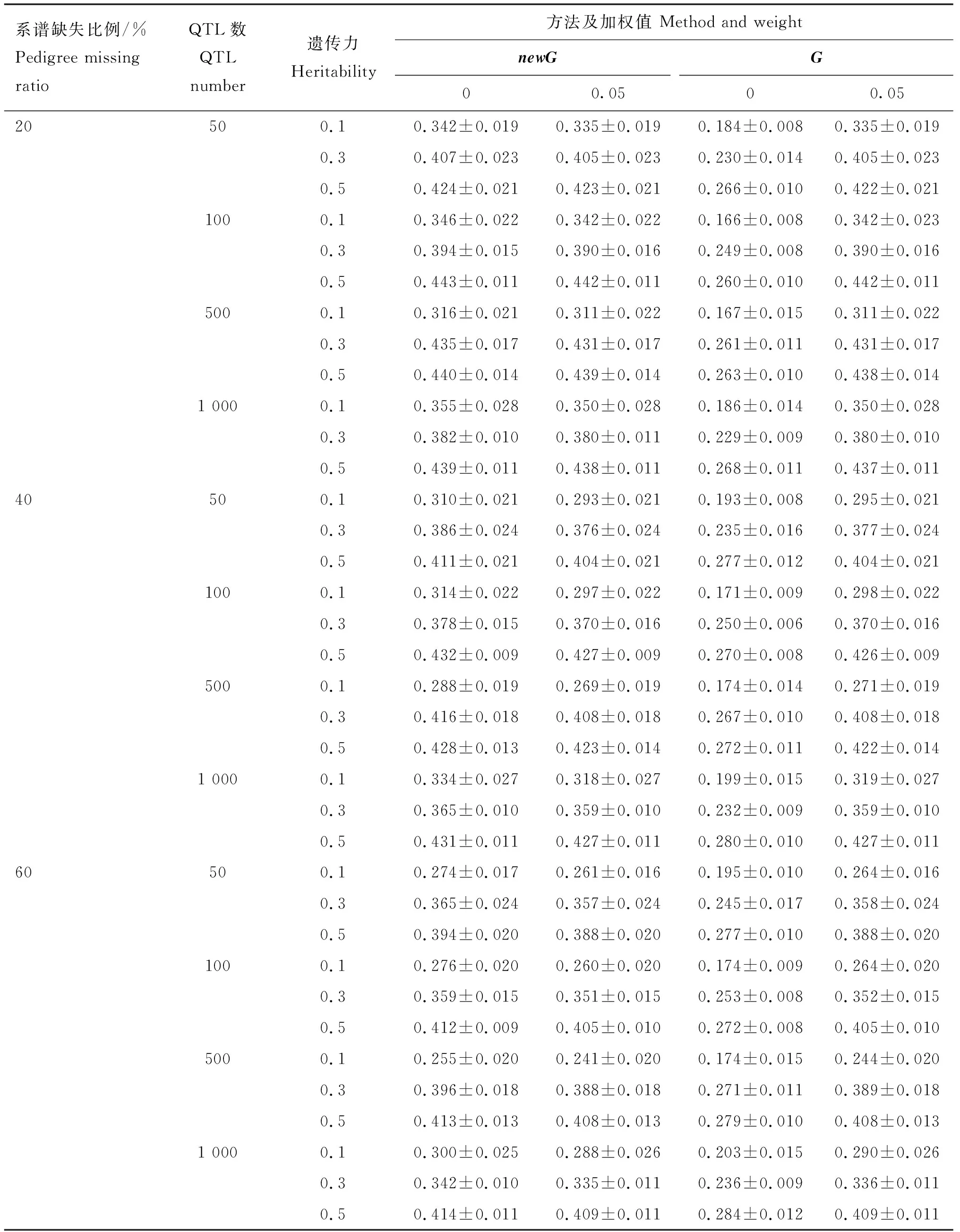
表5 基因分型个体系谱不同缺失比例下不同QTL数和遗传力下各模型的预测准确性(10次重复的均值)

不同基因分型个体系谱缺失比例下，newG阵较Gw阵的优势(预测准确性差值)变化见图1。可见，对于所有QTL数，随着h2降低，newG阵优势逐渐增加。这表明，在基因分型个体系谱部分缺失时，newG阵较Gw阵在低遗传力时优势更明显。

图1 基因分型个体系谱缺失(20%(A)，40%(B)，60%(C))时newG阵与Gw阵GEBV准确性差值

2.4 基因分型个体系谱全部缺失时各模型的预测准确性

基因分型个体系谱全部缺失，QTL数和h2变化时各模型的预测准确性见表6。可见，各QTL数及h2情况下，newG阵、newGw阵、Gw阵的准确性有轻微差异(±0.1%)，且均较G阵高。

表6 基因分型个体系谱完全缺失时不同QTL数和遗传力下各模型的预测准确性(10次重复的均值)

结合表3～表6可见，在不同比例的基因分型个体系谱缺失情况下，对于所有G阵，随着h2增加，预测准确性增加，而预测准确性随QTL数并没有明显变化规律。

3 讨 论

GS方法的模拟研究是其发展的重要过程，新方法实际应用之前，需要使用模拟数据对其电脑程序、算法及可靠性进行评估，为其实际应用提供参考。然而，数据模拟软件的设计及运行软件时的参数设置与真实情况往往有一定差异，使得模拟研究与实际应用的结果有偏差，如：在模拟研究中，非线性模型明显优于GBLUP法[34]，然而使用真实数据验证时，非线性模型较GBLUP只有轻微或没有优势[35]。本研究中，newG阵在模拟研究中显示出一些优势，而其还需要在实际数据中进一步验证。本研究模拟肉牛的多品种联合群体，对于其他单胎动物的多品种或同品种不同地区、不同国家的联合群体理论上仍然适用。

试验结果显示，不同模型的准确性随着h2的增大而提高，Luan等[36]使用实际数据应用GBLUP及Bayes模型时显示出了相似的结果，由此推测，低遗传力性状需要更多的表型来提高GEBV预测准确性。本试验中，不同模型的准确性随QTL数的变化无明显变化，在Daetwyler等[37]的模拟研究中，BayesB模型随着QTL数减少而准确性增高，GBLUP在不同QTL数时，准确性基本无变化。由此可以推测，这可能是由于GBLUP及ssGBLUP假设所有标记解释相同的效应方差，且无主效基因[16]，造成了本试验中应用G阵和newG阵时对QTL数的变化不敏感。

阻碍肉牛、绵羊等畜种实施GS的因素有：1)参考群体规模少；2)群体中同品种个体较少，群体中多品种混杂[40]；3)信息记录系统不完善，如：系谱记录，表型记录等[41]。因此，研究多品种联合或同品种不同地区联合实施GS是未来的趋势[25]。对于abGS，各品种间等位基因频率的差异会造成多品种联合群体出现大量HWDE位点[42]，目前还没有将HWDE考虑入GS的方法，本研究考虑HWDE因素构建基因组关系矩阵，在系谱部分缺失情况下具有优势，然而，HWDE对abGS的影响还有待进一步研究。

4 结 论

本研究针对abGS的G阵构建进行了探索，提出了一种G阵构建方法。结果表明，新型G阵在不需要加权的情况下就能达到常规G阵加权时的GEBV预测准确性，在系谱部分缺失时，应用新型G阵较加权常规G阵的GEBV准确性有一些提高。