变化环境下洪峰-洪量组合设计值计算方法研究

胡义明，梁忠民，姚 轶，罗序义，王 军，李彬权

(河海大学水文水资源学院，江苏 南京 210098)

工程水文计算是水利工程规划和建设的基础，国内外现行的工程水文计算理论与方法都要求水文极值系列具有平稳性。但受到气候变化及人类活动的影响，流域降雨时空分配模式、产汇流规律[1]及河道洪水的天然过程发生了改变，进而导致诸多站点水文系列呈现非平稳性变异[2-3]。理论上，现行的基于平稳性假定的工程水文计算理论与方法已不再适用于变化环境下的非平稳性情形[4-7]。

变化环境下非平稳性水文频率分析根据研究变量数目可以分为非平稳性单变量频率分析和非平稳性多变量频率分析。目前的研究主要集中在单变量方面，而关于非平稳性多变量洪水频率分析的研究还较少[7-9]。由于水文事件(过程)通常包含多个特征属性，如一场洪水过程包含洪峰和不同时段洪量特征等，采用单一水文变量(如洪峰或时段洪量)通常很难描述水文事件(过程)的真实特征，为此，进行变化环境下多变量洪水频率分析更具有现实意义。相较于平稳性多变量频率分析问题而言，非平稳性多变量频率分析问题要复杂得多。在平稳性条件下，洪峰-洪量联合分布函数被假定是唯一且不随时间变化的，指定重现期对应洪峰-洪量组合设计值易于求解。然而在非平稳性条件下，不同水文变量间的相关关系随着时间变化，即不同变量间的联合分布函数在不同年份是不同的，这导致了指定重现期对应的洪峰-洪量组合设计值求解困难[9-10]。目前基于非平稳性多维极值统计理论开展变化环境下多变量水文频率分析的研究正在兴起，但主要还是集中在描述不同变量间的相关结构、联合分布规律、极值事件对应重现期等特征随时间的变化过程[11-14]。而从设计洪水角度(指定设计标准对应唯一的洪水设计值)，在非平稳性多变量条件下推求指定标准的洪峰-洪量组合设计值的研究还较为缺乏[9，15]。

本文基于时变Copula函数构建了可综合考虑洪峰-洪量边缘分布非平稳性和变量间相关结构非平稳性的时变动态Copula多维联合分布模型，在此基础上，提出采用等可靠度法和条件期望组合法推求变化环境下指定标准的洪峰-洪量组合设计值，并以黄龙滩站洪峰和年最大7 d洪量系列为例进行了示例研究。

1 理论与方法

1.1 时变Copula模型

变化环境下多变量水文频率分析中的非平稳性包括各极值变量自身分布规律的非平稳性和不同变量间结构关系的非平稳性，而基于多维极值分布理论的时变Copula模型多被应用于描述变量边缘分布和结构关系的非平稳性中。在时变Copula模型中，各变量边缘分布中的参数及模型的结构参数不再是常数，其随协变量因子(如时间)而变化。通过时变Copula模型可构建综合考虑边缘分布非平稳性和变量间相依结构非平稳性的时变动态Copula多维联合分布函数，进而描述不同年份多变量联合分布规律的演变特征。

以变量X和Y分别表示洪峰和洪量，假定其对应的时变分布函数分别为Fx(x|θxt) 和Fy(y|θyt)，即：

xt～Fx(x|θxt)

(1)

yt～Fy(y|θyt)

(2)

式中：θxt、θyt——t时刻变量X和Y分布函数的参数集，其随时间变化，如对于具有3个参数的皮尔逊Ⅲ型分布而言，θxt={αxt,βxt,γxt}。

时变Copula模型的结构参数θc假定为时间的线性函数，即：

θct=b0+b1t

(3)

则时变Copula模型可表示为[16]

Fxy(x,y|θxt,θyt,θct)=C(Fx(x|θxt)Fy(y|θyt)|θct)=C(μt,vt|θct)

(4)

其中μt=Fx(xt|θxt)vt=Fy(yt|θyt)

式中：C(·)——联合累计分布函数；θct——t时刻的时变Copula模型结构参数；μt、vt——t时刻变量xt和yt对应的概率值；b——系数。

由于Gumbel Copula函数适用于变量间存在正相关的情形，且可较好地描述变量间上尾部相关性等优点[16]，为此基于Gumbel Copula函数构建描述非平稳性洪峰-洪量联合分布的时变Gumbel Copula多维联合分布模型：

C(μt,vt|θct)=exp{-[(-lnμt)θct+(-lnvt)θct]1/θct}θct≥1

(5)

式中：θct——t时刻Gumbel Copula模型的结构参数。

相应的联合概率密度函数c可表示为

c(μt,vt|θct)=C(μt,vt|θct)μt-1vt-1[(-lnμt)θct+(-lnvt)θct](-2+2/θct)·

[lnμtlnvt]θct-1{1+(θct-1)[(-lnμt)θct+(-lnvt)θct]1/θct}

(6)

在给定X=xp条件下，变量Y的条件概率密度函数fY|X(·)可表示如下：

fY|X(Y|X=xp,θyt,θct)=C(μp,vt|θct)μp-1vt-1[(-lnμp)θct+(-lnvt)θct](-2+2/θct)

(lnμplnvt)θct-1{1+(θct-1)[(-lnμp)θct+(-lnvt)θct]1/θct}fy(y|θyt)

(7)

其中μp=fx(xp|θxt)

公式中参数的估计采用分步法思想，即首先估计边缘分布函数中的参数，然后再估计时变Copula函数中的结构参数。

由式(5)可以看出，当采用时变Gumbel Copula模型描述洪峰-洪量联合分布规律随时间演变的非平稳性特征时，会导致洪峰-洪量联合分布在不同年份是不同的。对于给定的X=xp，Y对应的条件概率分布fY|X(Y|X=xp,θyt,θct)在不同时刻也是不同的。因此，本文研究的核心问题为在给定某一标准洪峰设计值X=xT条件下，计算X对应Y的设计值y相应，进而获得洪峰-洪量的组合设计值(xT，y相应)。

1.2 等可靠度法

等可靠度法是一种变化环境下单变量水文设计值估计方法。该方法认为虽然环境变化导致了水文极值的非一致性，但根据非一致性水文极值系列推求的水文设计值所具有的水文设计可靠度不应该被降低，至少应与现行一致性条件下频率计算方法提供的设计值具有相同的可靠度，进而通过可靠度指标将设计值估计与工程使用年限联系起来，一定程度上降低了时变概率分布模型随时间外延而给设计值估计带来的不确定性[17]。

以RS表示一致性条件下，工程设计年限L和设计重现期T对应的水文设计可靠度，则有：

(8)

以RNS表示非一致性条件下，工程设计年限L和设计重现期T对应的水文设计可靠度，则有：

(9)

式中：Ft(x)——第t年水文极值的概率分布函数。

根据等可靠度方法，令RNS=RS，即：

(10)

通过求解式(10)，即可获得非一致性条件下的设计值XT,NS。

1.3 条件期望组合法

根据洪峰-洪量联合分布的概率密度函数，可以推求给定X=xp条件下Y的条件概率密度函数(式(7))。假定主控变量为X，其对应的流量值为xp，则可采用式(11)推求xp对应Y的条件期望值yt,E，(xp，yt,E) 即为X和Y的条件期望组合：

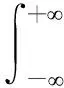
(11)

需要注意的是，由于式(11)中条件概率密度函数fY|X(·)是随时间变化的(式(7))，因此，在不同时刻计算得到的期望值yt,E是不同的。

1.4 基于等可靠度法和条件期望组合法的洪峰-洪量组合设计值

由于主控变量X的分布函数Fx(x|θxt)是时变的，为此，对于指定的不超过概率p，主控变量X对应的分位点xp随着时间也是变化的，即：

(12)

根据式(12)计算获得不同时刻主控变量X对应的分位点xt,p后，再结合式(12)可计算得任一时刻xt,p对应的变量Y的期望值yt,p。即获得标准p条件下，任一时刻主控变量X与次要变量Y的条件期望组合为(xt,p,yt,E)。

根据期望组合(xt,p,yt,E)样本系列，可获得p条件下xp和yE间的统计关系，即:

yE=f(xp)

(13)

对于指定设计标准(重现期T)，T=1/p。采用等可靠度法计算主控变量X的设计值xT，随后通过条件期望组合关系(式(14))，获得给定设计值xT条件下次要变量Y对应的条件期望值yT,E。计算获得的组合设计值(xT,yT,E) 即为非一致性条件下，重现期T对应的主控变量X和次要变量Y的期望组合设计值。

yT,E=f(xT)

(14)

2 实例分析

以黄龙滩站1956—2014 年共 59 年的洪峰和年最大7 d洪量系列为对象进行实例分析。黄龙滩站位于汉江支流堵河的下游，控制流域面积为11 140 km2，占整个堵河流域面积的95%左右。由于该流域的竹溪河水库及潘口、松树岭等水电站的运用，导致不同时期洪水形成条件发生变化。图1为洪峰系列和年最大7 d洪量系列，从图1可以看出洪峰系列和年最大7 d洪量系列存在明显的下降趋势，在0.05显著性水平下，Mann-Kendall统计量的计算值分别为-3.35和-2.72，其绝对值均大于0.05显著性水平下对应的阈值1.96。

图1 洪峰和年最大7 d洪量系列Fig.1 Time series of flood peak and 7-day flood volume

为了描述非平稳性洪峰和年最大7 d洪量的分布特征，构建了基于广义极值分布函数(GEV)的变参数概率分布函数模型。在该模型中，GEV分布函数的位置参数或尺度参数随时间变化，而形状参数为常数。模型参数采用贝叶斯方法并结合MCMC抽样技术进行估计，以最大后验估计作为模型使用参数。在抽样过程中，平行运行5条链，每条链上抽取10 000个样本(每条链都已满足收敛要求)，去掉预热的9 900个样本，每条链上仅采用最后的100个样本，5条链共计500个样本值，其中使参数后验密度值达到最大的即参数的最大后验估计[18]。采用赤诚信息准则(AIC)指标对模型的拟合效果进行评估，结果见表1。从表1可以看出，对于洪峰系列，GEV2模型的AIC值最小；而对于年最大7 d洪量系列，GEV1模型的AIC值最小。因此，洪峰和年最大7 d洪量系列对应的最优模型分别为GEV2和GEV1。

表1 AIC指标值计算结果

进一步采用Wormplot指标对基于广义极值分布函数的变参数概率分布函数模型的拟合效果进行评估，结果见图2。从图2可以看出，无论是洪峰系列还是年最大7 d洪量系列，偏差点据基本都落在90%置信限组成的区域内，表明该模型的拟合效果较好。

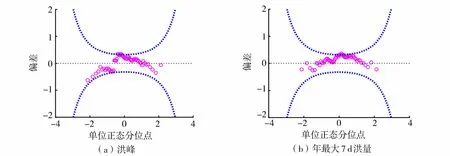
图2 变参数概率分布函数模型的拟合效果Fig.2 Fitting performance of probability density distribution function with variable parameter

图3为在0.02、0.05和0.1超过概率Ep下，洪峰和年最大7 d洪量分位数随时间的演变特征。从图3可以看出，无论是洪峰还是7 d洪量，不同超过概率条件下分位点估计值都随时间不断减小，这与实测系列呈减小趋势相吻合。

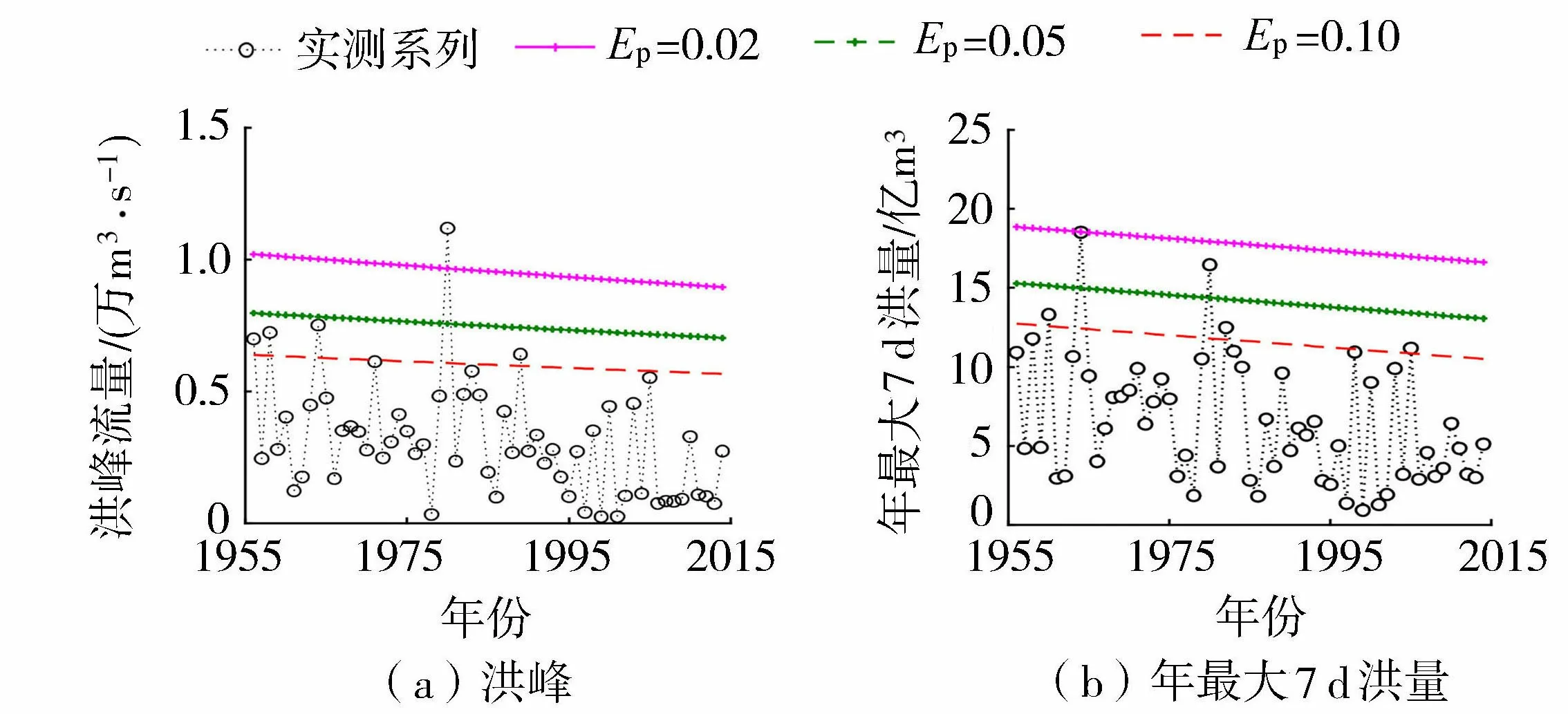
图3 不同超过概率下洪峰和年最大7 d洪量分位数随时间演变特征Fig.3 Evolution characteristics of flood peak and maximum 7-day flood volume over time with different exceedance probability

图4为洪峰和年最大7 d洪量对应的分布函数中参数的时变过程及Copula模型结构参数的时变过程。其中Copula模型结构参数的估计同样也采用了贝叶斯方法并结合MCMC抽样技术，与各变量分布函数中的参数估计类似。

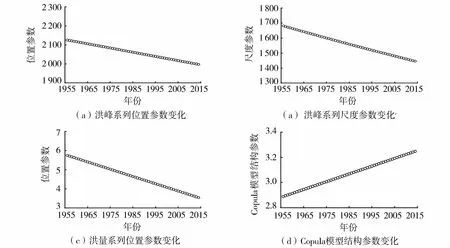
图4 洪峰、洪量边际分布参数及Copula模型结构参数的时变过程Fig.4 Time-varying process of marginal distribution parameters of flood peak/ flood volume and time-varying process of Copula dependence parameters

图5为1956—2014年不同联合概率(0.2、0.4、0.6、0.8和0.95)条件下，洪峰和年最大7 d洪量联合分布规律随时间演变特征。从图5可以看出，对于指定联合概率(如0.95)而言，其对应的洪峰-洪量联合分布规律从1956年开始随时间发生左移，即同一概率对应的洪峰-洪量联合分布特征随时间是变化的。

图5 1956—2014年洪峰和年最大7 d洪量联合分布随时间的演变特征Fig.5 Evolution characteristics of joint distribution of flood peak and maximum 7-day flood volume over time from 1956 to 2014

以年最大7 d洪量为主控变量，根据其对应的变参数概率分布函数模型，可计算任一时刻t指定超过概率Ep对应的分位数xt,p。本文计算了t为1956—2014年，在超过概率0.02、0.05和0.10条件下，不同年份年最大7 d洪量的分位数值xt,p(图3)。根据式(12)，计算任一年份洪量分位数xt,p对应的洪峰的期望值yt,E，进而获得了指定Ep条件下年最大7 d洪量和洪峰的条件期望组合系列(xt,p,yt,E)。通过拟合洪峰-洪量期望组合系列，可获得Ep对应的洪峰-洪量期望组合关系曲线。图6为超过概率0.02和0.05(对应重现期分别为50 a和20 a)条件下，洪峰和年最大7 d洪量的期望组合关系曲线。从图6可以看出，不同重现期下拟定的洪峰-洪量期望组合关系曲线均能很好地拟合期望组合点据。

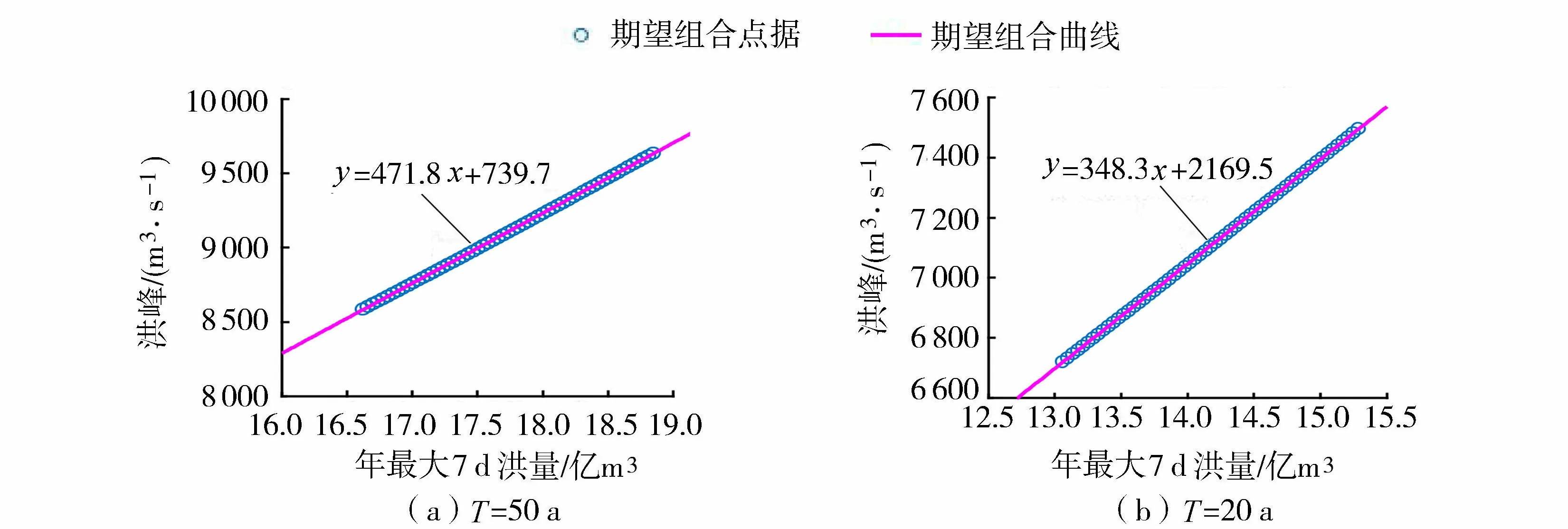
图6 指定重现期条件下的洪峰-洪量期望组合关系曲线Fig.6 Expected combination relationship curve of flood peak and flood volume corresponding to specified return periods

基于等可靠度方法，计算年最大7 d洪量(主控变量)在不同工程设计年限L(20 a、30 a、40 a和50 a)和不同设计重现期T(10 a、20 a和50 a)条件下的设计值，并结合指定重现期条件下的洪峰-洪量期望组合关系曲线，计算不同工程设计年限和不同设计重现期条件下，洪量设计值对应的洪峰条件期望值，得到了指定重现期和工程设计年限对应的洪峰-洪量设计值的期望组合结果如表2所示。

表2 不同设计标准及工程设计年限条件下洪峰-洪量设计值的期望组合结果

从表2可以看出，随着工程设计年限的增加，指定重现期对应的主控变量(年最大7 d洪量)设计值呈减小变化，这与年最大7 d洪量系列呈减小趋势的实际情况符吻合。同样，随着工程设计年限的增加，指定重现期下洪量设计值对应的洪峰条件期望值也呈减小变化，这也与洪峰系列呈减小趋势的实际情况相吻合。总体来看，指定重现期对应的洪峰-洪量设计值期望组合随着工程使用年限的增加而呈减小趋势，这是由于洪峰和洪量系列本身呈减小趋势导致。

3 结 论

a.针对变化环境下洪峰和洪量系列的非平稳性，基于Copula函数，构建了可综合考虑洪峰和洪量边缘分布非平稳性及洪峰-洪量相关结构非平稳性的时变动态Copula模型，分析了洪峰-洪量联合分布特征随时间的非平稳性演变规律。黄龙滩站实例研究结果表明，在相同的联合概率条件下，洪峰和年最大 7 d洪量联合分布特征在不同年份是不同的，其随时间变化显著。

b.为了解决平稳性条件下多变量组合设计值计算方法不适用于变化环境下非平稳性情形的难题，提出基于等可靠度法和条件期望组合法的变化环境下洪峰-洪量组合设计值计算方法。黄龙滩站实例研究结果表明，指定重现期对应的洪峰和年最大 7 d洪量设计值的期望组合随着工程使用年限的增加而呈减小趋势，与洪峰和洪量系列本身呈减小趋势吻合，同时也表明非平稳性条件下设计洪水计算需要考虑工程使用年限的影响。

c.作为示例性研究，本文在非一致性洪峰和洪量的边缘分布函数构建中，选用了具有较好拟合效果的基于广义极值分布函数的时变概率分布模型。在该时变模型中，仅考虑了时间因子对分布函数中参数的影响，而没有考虑其他因子(如降雨、下垫面变化等)的影响。在非一致性洪峰-洪量联合分布规律描述方面，鉴于Gumbel Copula函数可较好地描述变量间上尾部的正相关性优点，构建了基于Gumbel Copula函数的时变动态Copula模型，而没有综合分析其他不同Copula函数。在以后的研究中，将进一步考虑基于不同类型分布函数、分布函数中参数的不同驱动关系及不同类型Copula函数，通过对比优选的方式确定优势边缘分布和联合分布模型。