智能反射面辅助的上行NOMA系统低功耗传输方案研究

马昊淳，王 鸿

（南京邮电大学通信与信息工程学院，江苏南京 210003）

随着5G在全球范围内的部署，后5G（B5G）以及6G的研究引起了学术界与工业界的广泛关注。未来的通信业务要求更高的通信速率、更多的连接密度以及更低的时延，很多新兴技术［1］被认为是未来通信系统的潜在技术方向，例如非正交多址接入（NOMA）技术［2－3］、massive MIMO［4］技术等。 此外，为了满足未来更高的频谱效率与能量效率需求，众多研究机构的6G白皮书都将智能反射面（IRS）视为潜在的关键技术［5－7］。

IRS是一种由大量低成本的无源反射元件组成的二维平面，置于基站与用户（发送方与接收方）之间，每个无源反射元件都可以独立地改变入射信号的相位和幅度，使用户能够更好地接收来自基站的信号，同时也能更好地向基站发送信号。IRS使得原本随机的通信信道变得可控，打破传统意义上信道对通信链路起负作用的认知。并且，IRS技术具有很强的兼容性，可以与很多技术融合使用［8］。

鉴于IRS与NOMA都是未来通信的关键技术，两者的结合可进一步提升系统频谱与功率效率，进而通过联合优化基站的有源波束和IRS的反射波束可以提升系统的性能，如最大限度地提升NOMA用户的最低速率，提升NOMA用户的能效，降低基站或者终端的发射功率等。文献［9］表明，相比于传统的正交多址接入（OMA）系统，IRS辅助的NOMA系统不管在系统吞吐量还是在发射功耗方面都能够获得更好的性能。

在已有的NOMA系统中，一般都是利用已知的信道状态信息被动地进行收发机设计，在IRS辅助NOMA系统中，IRS的引入增加了系统优化的自由度，将传统的被动设计模式转变为主动设计模式，构建出收发机与无线环境联合优化新模式。文献［10］研究了IRS辅助的下行NOMA系统，其目标是在每个用户的最小信干噪比（SINR）的约束下，将基站的发射功率降到最小，并提出序列旋转算法用于确定相移变量。仿真结果表明，与IRS辅助的OMA系统相比，IRS辅助的下行NOMA系统可以显著降低基站的发射功率。与文献［10］不同，文献［11］所研究的是IRS辅助的上行NOMA系统，且基站与用户之间不存在视距路径（LoS），其目标是在最大发射功率的约束下，最大化所有用户的和速率。通过在用户处进行联合功率控制，在IRS处进行波束成形设计，并采用半定松弛法得到该问题的次优解。仿真结果表明，与IRS辅助的OMA系统相比，基于IRS辅助的NOMA系统可以达到更高的和速率。此外，文献［12］使用差分凸规划（DC）算法有效地解决了非凸二次规划问题，该算法通过交替优化求解，其仿真结果表明，IRS辅助的NOMA系统在同等条件下能够使基站的发射功率更小。文献［13］研究的是IRS辅助的下行NOMA系统，目标是在速率最大化和发射功率最小化之间作一个平衡，从而提高信号传输的能量效率，通过联合优化基站处的波束成形与IRS处的相移变量使得系统的能效达到最大。仿真结果表明，与传统的IRS辅助OMA系统相比，IRS辅助的NOMA系统具有更好的性能。文献［14］针对双小区 IRS辅助NOMA场景，研究目标是使两个小区边缘的用户以及小区内部用户的发射功率之和最小化，该文献将功率分配和相移的联合优化问题转化为纯相移问题，提出一种低复杂度的封闭式求解方法来解决问题。仿真结果表明，该算法下所得到的功耗小于各种基准测试方案的功耗。文献［15］研究了IRS辅助NOMA系统的上行链路的中断性能，考虑所有用户都有LoS路径和非LoS路径，并且所有路径都经历 Nakagami⁃m衰落，通过矩匹配将NOMA用户的接收功率近似为伽马随机变量。仿真结果表明，在特定条件下IRS可能会降低具有LoS路径用户的性能，而使非LoS路径用户的性能得以提升。

综上所述，IRS与NOMA技术都是未来通信系统的潜在技术，将两者的深度融合更是研究的热门。目前的研究涵盖了上行和下行系统，包含很多种目标函数，其中能效问题、速率最大化问题和功率最小化问题最为常见。已有研究中解决问题的关键是通过交替优化基站处的波束成型以及IRS处的相移变量，实现不同的研究目标。然而，在现有研究中，未能充分发挥IRS与NOMA在功率效率方面的优势，低功耗传输仍将是未来无线通信不懈追求的指标。本文针对已有文献的不足，深入研究IRS辅助的NOMA系统的低功耗传输方案。本文的创新之处在于：在用户差异化服务质量（QoS）约束条件下，建立IRS辅助的NOMA系统上行总发射功率最小化问题。进一步地，利用优化问题的特性，推导出功率分配系数与相移矩阵之间的关系，将原功率分配与相移的联合优化问题转化为纯相移优化问题。最后，求解Max⁃Min优化问题得到系统的最优相移。仿真结果表明，提出的联合优化方案可以显著降低IRS辅助NOMA系统的上行发射功率，且功耗降低值随着发射单元数目的增加而增加。

1 系统模型

如图1所示，本文考虑IRS辅助的上行NOMA系统，包含1个基站、K个用户、1个IRS。基站位于小区的中心，其覆盖范围是半径为R的圆形区域。为了避免近场效应，所有用户随机地分布在覆盖半径从Rn到R范围内，基站和用户均配备1根天线，其与用户k之间的距离为dB，k。 IRS位于基站覆盖范围内，拥有的反射单元数目为N，其与基站之间的距离为dB，I。 智能反射面通过改变入射信号的延时，来操控入射信号的相位偏移。由于无线信道中复杂的传播环境，包括反射、折射等，入射到反射面的电磁波可能包括来自多条路径、多个方向。智能反射面的作用就是改变这些信号相位，从而在基站接收端实现信号的增加或干扰的削弱。

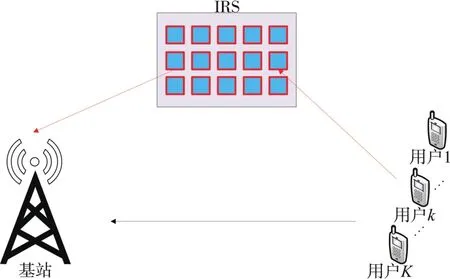
图1 系统模型框图

用户随机分布在基站的覆盖区域内，假设基站⁃用户的连线与基站⁃反射面的连线之间的夹角为ξ，可知：∈ ［0，2π）。 由余弦定理知，用户k与反射面之间的距离为

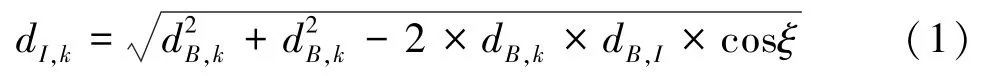
那么，用户k⁃反射面连线与基站⁃反射面连线之间的角度ω可以求解为

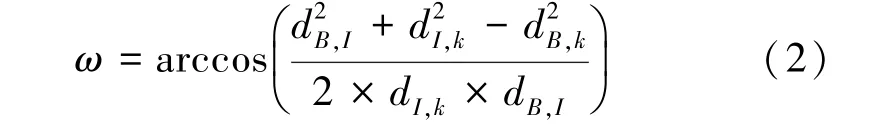
不失一般性，将用户按照初始化信道增益降序排列。

由于较大的路径损耗，被IRS反射两次及两次以上的信号忽略不计。因此，基站处所接收到的信号可以表示为

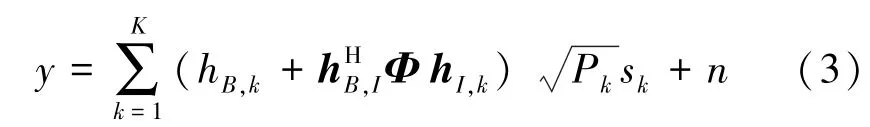
其中，hB，k为基站与用户 k之间的信道增益，hB，I∈CN×1为基站与 IRS 之间的信道增益， hI，k∈ CN×1为用户k与IRS之间的信道增益，Pk为用户k的发射功率，sk为归一化的功率信号，n表示噪声，其服从均值为0、方差为σ2的复高斯分布，IRS相移矩阵表示为 Φ ＝ diag｛λ1ejφ1，…，λNejφN｝， 是一个对角矩阵。 其中λn≤1，φn∈［0，2π），考虑系统实施的复杂度，本文只考虑IRS相移改变的情况，因此，λn＝1，即相移矩阵可以简化为

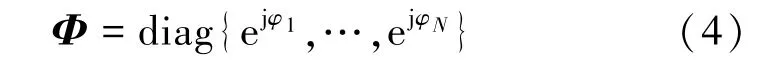
无线信道包含路径损耗和小尺度衰落，信道增益可以建模为：h＝d－β／2g，其中，d为发送方和接收方之间的传播距离，β为路径损耗指数，g为小尺度衰落系数。因此，基站与用户k之间的信道增益可以表示为：其中， gB，k服从均值为0、方差为1的复高斯分布，即 CN（0，1）；IRS与用户 k 之间的信道增益可以表示为：其中，gI，k服从 CN（0，1）； 由于基站与IRS 之间存在LoS，其信道增益建模为莱斯衰落模型，即 hB，I＝， 其中 g0表示 LoS 分量的信道增益，gB，I表示非LoS多径导致的小尺度衰落，服从 CN（0，1）。 于是，信道增益可以分别表示为

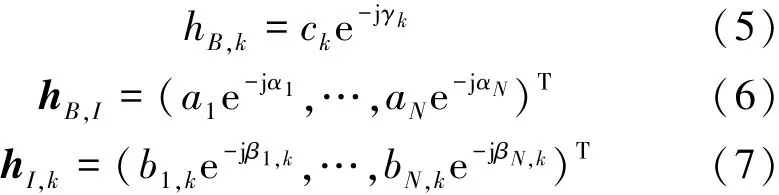
为保证NOMA解调次序不变，所设计相移变量Φ仍需满足用户的信道增益按照降序排列，即

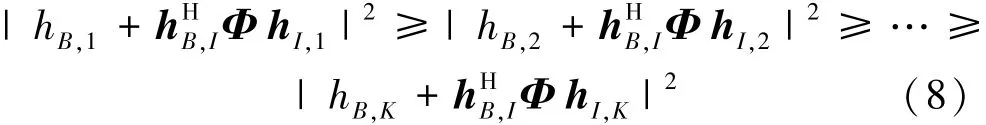
根据NOMA系统的工作原理，基站先解调信号强的用户，解调完成后删除已调用户信号，依此类推，直到所有用户信号都被解调。那么，用户k处的SINR可以表示为

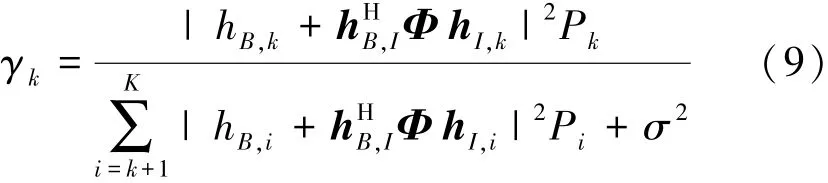
其中，当k＝K时，无NOMA用户干扰。即

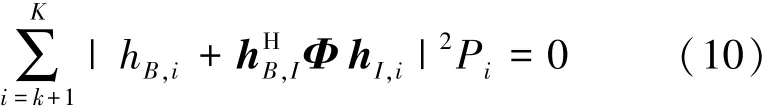
2 问题建立及其解决方法

在本节中，首先在用户差异化QoS约束条件下，建立IRS辅助的上行NOMA系统功率最小化问题，然后推导出各个用户发射功率与IRS处相移变量之间的关系式，并将原始的优化问题转化为纯IRS的相移优化问题，进而提出一种Max⁃Min算法解决IRS的相移优化问题。

2.1 问题描述

本文旨在解决的问题是通过联合设计IRS处的波束成形与用户的功率控制，最小化系统的总发射功率，因此优化问题可以表示为

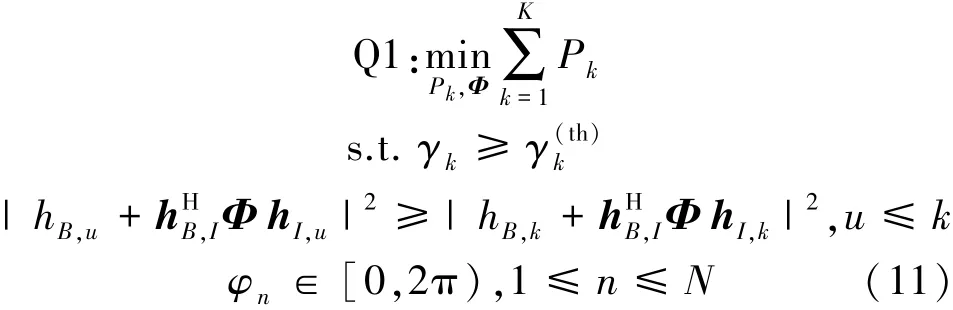
2.2 原始问题转化

当原始优化问题取得最优解时，约束条件γk≥等式成立，即

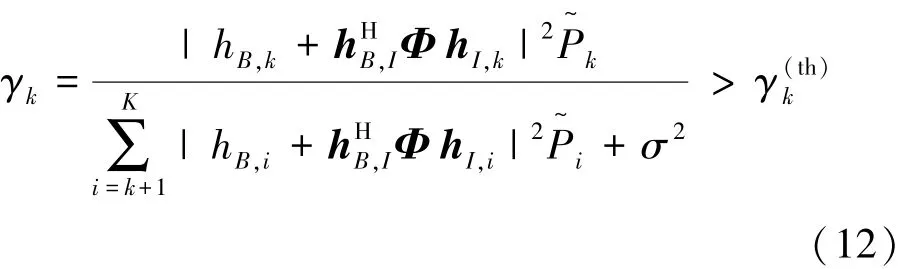
由上述证明可以得到

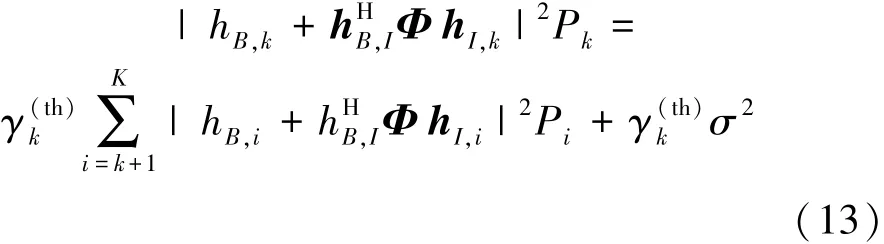
为了将式（13）写成更加压缩的形式，分别定义了相位偏移向量

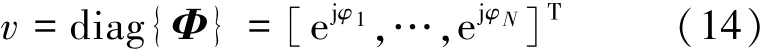
级联信道信息

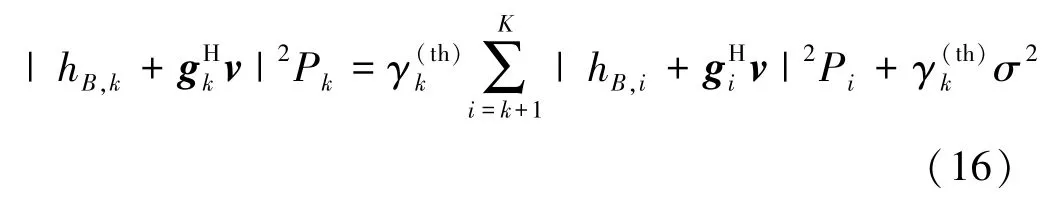
为了将式（16）写成更加压缩的形式，令

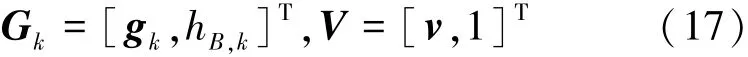
进而等式（13）可以转化为

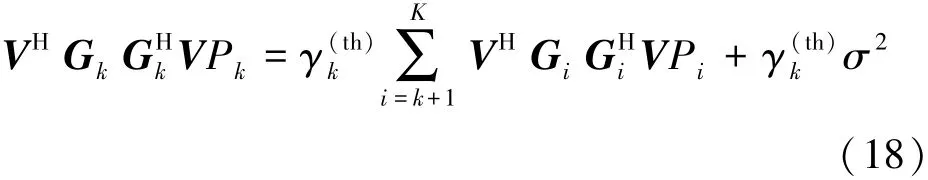
因此，第K个解调用户所需发射功率可以表示为

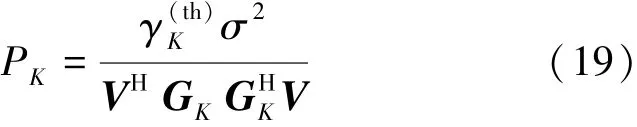
于是，第k个解调用户所需发射功率可表示为

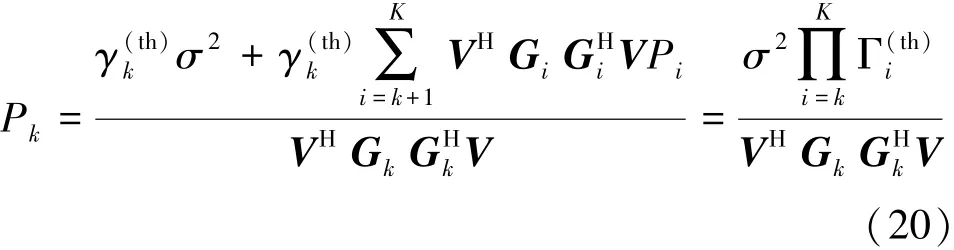
将式（19）、式（20）代入问题Q1中，则优化问题可以转化为

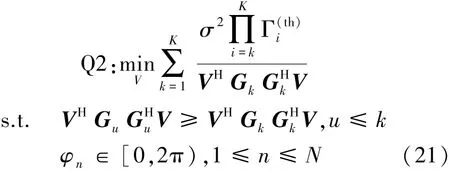
可以看出，问题Q2中的优化变量只含相移矩阵V。

2.3 问题Q2的解决方法

由于优化问题Q2中的目标函数和约束条件均为非凸，所以优化问题Q2为非凸问题，很难求出该问题的最优解，因此本节提出一种Max⁃Min算法，将目标函数进行转化，通过迭代求出最优解。

将式（20）转化为

由于式（22）等式右边是一个常数，因此，若想使功耗 Pk最小化，只需要使 VHGkGHkV最大化即可。

建立优化问题

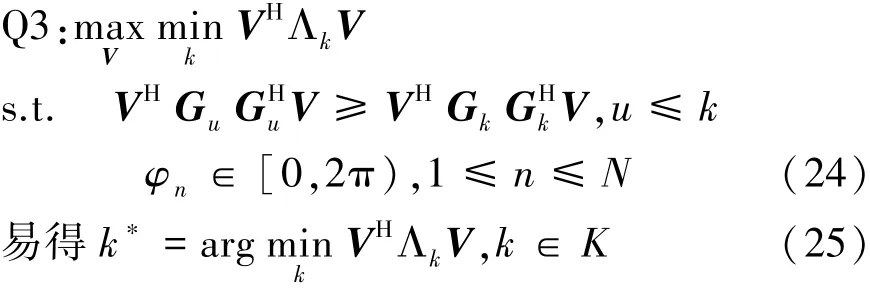
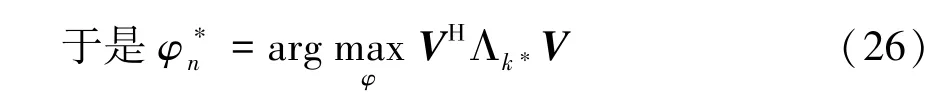
将式（5），（6），（7）代入 Q3的目标函数中，可得

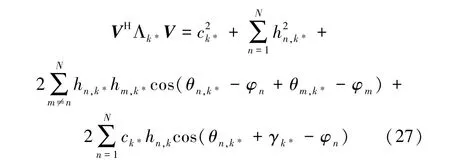
当最优相位设计完成时，将其代入式（20）中，便可得到每个用户的发射功率。

3 仿真结果分析

本节分别在零相移与随机相移的情况下，验证本文所提出的算法对系统总发射功率的影响，并与以下多种方案进行对比：零相位IRS辅助NOMA系统，随机相位 IRS辅助 NOMA系统，无 IRS辅助NOMA系统。本文所使用仿真参数如表1所示。

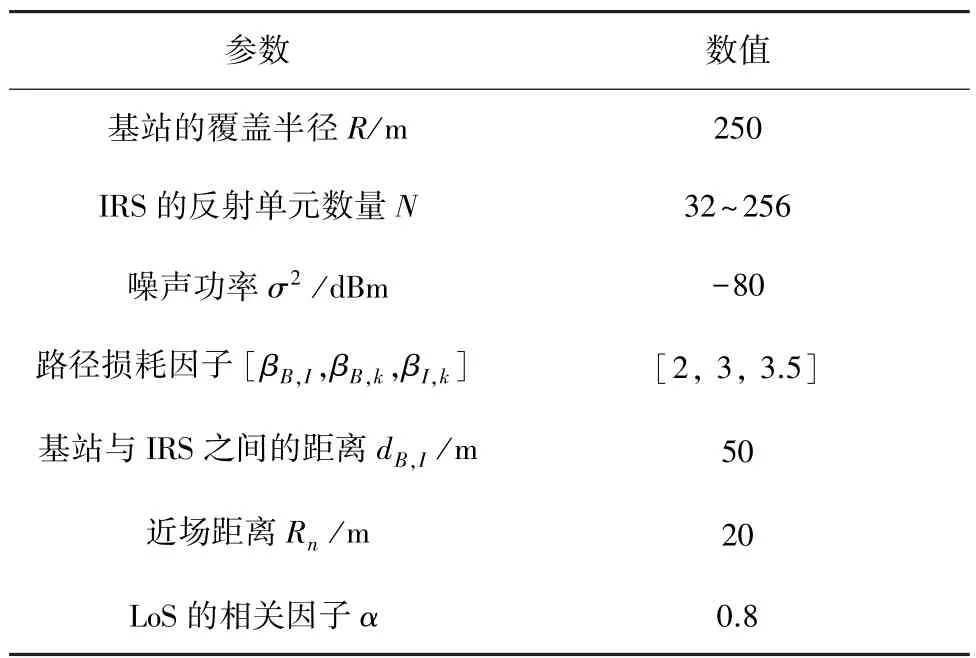
表1 仿真参数

图2画出了反射单元数N为128的条件下，不同SINR阈值时3个用户系统所需的发射功率。从图2中可以看出，使用 IRS辅助的上行NOMA系统的总发射功率比没有IRS辅助的上行NOMA系统的总发射功率要小，其原因是 IRS具有增强有用信号、抑制干扰信号的功能。同时，与没有IRS辅助的系统相比，本文所采用的相移优化算法可以降低总发射功率约8 dBm；与使用随机相位和零相位的IRS辅助系统相比，本文所采用的Max⁃Min相移优化算法可以降低总发射功率约5 dBm。此外，从图2中还可以看出，对于随机相位的IRS与零相位的IRS辅助系统来说，两者的总发射功率十分接近。在给定两种不同的初始相位时，采用Max⁃Min相位优化算法得到的发射功耗是相等的。

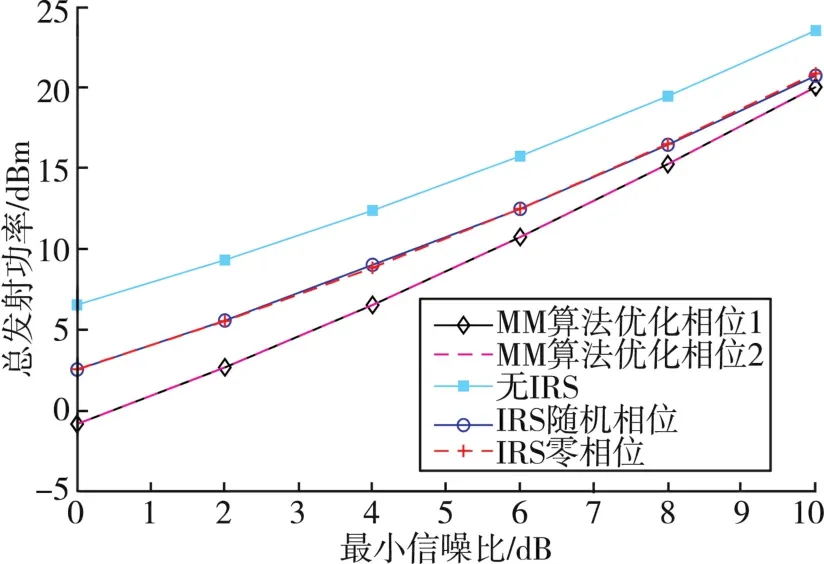
图2 K＝3，N＝128下，不同SINR时功耗比较

图3对比了在不同的SINR需求下，OMA系统与NOMA系统的总发射功率，其中用户数为3，反射单元数为128。从图3中可以看出，无论是OMA系统，还是NOMA系统，在使用IRS辅助传输时都比未使用IRS辅助传输消耗的功率低，进一步说明IRS可以增强有用信号的强度。本文中OMA系统采用频分多址接入（FDMA）技术，在满足用户的差异化QoS的前提下，IRS辅助的NOMA的发射功耗低于IRS辅助的OMA系统。

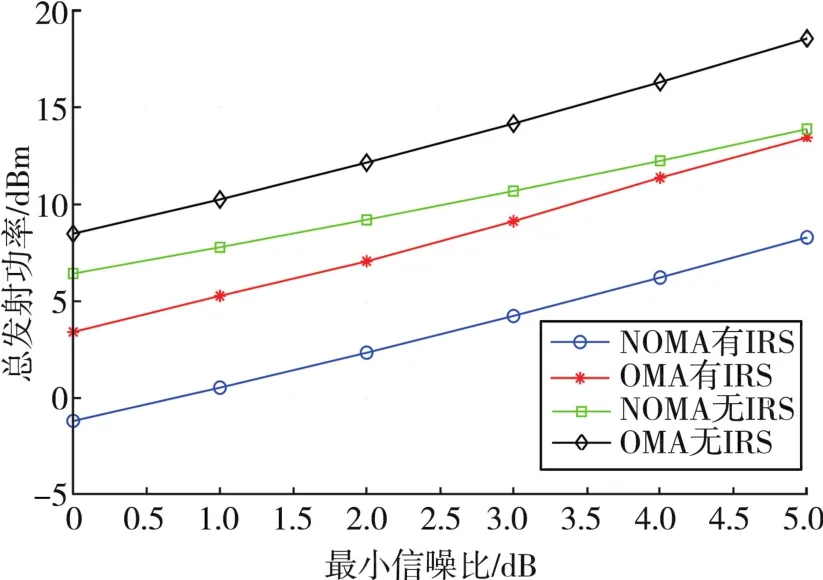
图3 K＝3，N＝128下，OMA与NOMA系统的功率比较

图4画出了在给定用户最小SINR的前提下，IRS反射单元数量与系统发射功耗之间的关系，用户数量K为3，最小SINR阈值为5 dB。可以看出，系统的发射功耗随着IRS反射单元数量的增加而减少，这是由于IRS可以增强有用信号的强度。从图4中还可以观察到在无IRS辅助的NOMA系统中，发射功耗并不会随着IRS反射单元的增加而有所改变，这也是显而易见的。另外，在发射功耗方面，本文提出的方案要明显优于其他基准方案。

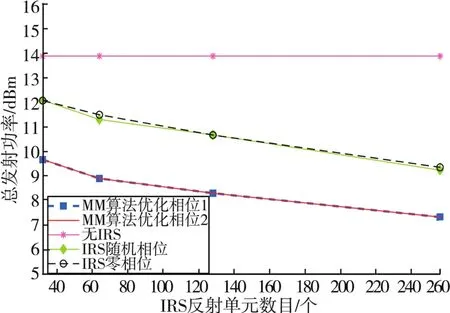
图4 K＝3，＝5 dB下，反射单元数N与功耗的关系

4 结束语

本文在满足各个用户差异化QoS的前提下，通过对用户的功率控制和IRS的相移联合优化，使得IRS辅助的NOMA系统的上行发射功耗最小化。由于原始问题及约束条件均为非凸的，很难直接求解，利用优化问题的特性，推导功率分配系数与相移矩阵之间的关系，将原问题转化为纯相移优化问题，进而采用Max⁃Min算法对IRS处的相移变量进行优化。仿真结果表明，与多种基准方案相比，本文提出的联合优化方法可以有效地降低系统的发射功耗，且随着反射单元数目的增加，发射功耗逐渐降低。