基于故障数据的重庆地铁车辆检修排班计划优化研究

刘 杰

（重庆工程职业技术学院 智能制造与交通学院，重庆 402260）

随着重庆地铁车辆检修进入智能化运维时代，利用车辆智能运维系统采集和处理的数据信息来提高安全水平和生产效率成为车辆检修发展的主要目标。Wildeman等[1]从节省成本角度提出了一种将系统长期维修计划和短期维修计划综合考虑的动态成组维修策略。Do等[2]以可靠度为约束建立了多系统的动态维修策略优化模型。Shafiee等[3]提出了一种基于役龄相关的多系统成组维修优化模型，并将其应用到轴承预防维修方面。戈春珍[4]利用故障数据对车辆预防检修周期和临检策略2方面进行优化研究。徐万宝[5]针对车辆门系统提出了相应的故障预测和健康管理框架。王茂正等[6]利用车辆基地智能综合管理系统对车辆检修日计划进行编制。龙翔宇[7]建立了车辆检修与运用计划的协同优化模型。现有研究多集中在车辆维修策略优化、故障预测、车辆检修日计划编制和车辆运用计划等方面，鲜有对车辆检修工班组排班计划优化的研究。在车辆故障处理数据基础上，综合运用统计学和优化理论构建车辆检修工班组排班计划模型并设计算法求解，以重庆6号线为例进行验算和分析。

1 车辆检修排班计划参数与故障处理时间分析

1.1 排班计划参数设定

重庆地铁6号线车辆检修工班组根据修程的要求分为列检、均衡修和专项修3种类型。在工班组数量配置方面，列检工班共有4组，分别为列检A班、B班、C班、D班；均衡修工班共有3组，分别为均衡修A班、B班、C班；专项修有1个工班组。所有工班组排班计划按两班制模式，即将1个工作日24 h分为白班和夜班，其中白班工作时间为9 : 00—17 : 30，夜班工作时间为17 : 30至次 日9 : 00。列检工班组排班计划采用“白夜休休”模式，即上1个白班和1个夜班后连续休息2个工作日，如此重复。均衡修和专项修工班组均采用“长白班”模式，即连续上5个白班后休息2个工作日，如此重复。在利用各工班组故障处理时间数据信息基础上，综合考虑故障处理时间表示、修程类别、企业要求和员工休息时间保障等约束条件对已有排班计划进行优化调整。为了简化研究，假设故障发生情况已知，给出部分变量符号进行说明。xijm表示指派工班组m在工作日i时段j当班；yijnk表示修程k中故障n在工作日i时段j发生数量，个；zijmn表示指派工班组m在工作日i时段j处理故障n数量，个；tmn表示工班组m处理故障n的时间，s。

根据重庆6号线实际情况，确定部分下标变量取值为m= 1，2，…，8，其中m= 1，2，3，4分别表示列检A班、B班、C班、D班；m= 5，6，7分别表示均衡修A班、B班、C班；m= 8表示专项修1个工班组；k= 1，2，3分别表示列检修程、均衡修修程和专项修修程；j =1，2分别表示白班时段和夜班时段。

1.2 故障处理时间分析

将工班组在一段时间内对故障的处理时间看作随机，根据其非负连续的特点选用相位分布对数据进行拟合，从而得到故障处理时间分布函数F如公式⑴所示。

式中：α= （α1，α2，…，αQ），α为系数向量且满足，其中Q为PH分布的阶数；R为Q阶方阵，即R= （ruv）Q×Q，满足Rw≤0，ryv＜0和ruv≥0，u≠v；w为元素均为1的列向量，且w= （1，1，…，1）Q×1；N为故障数量。

相位分布模型在理论上可无限逼近任意非负随机变量的真实分布，然而，由于需要确定的参数过多，不便于实际应用。Weerstra[8]给出了一种简化的计算方法来确定相位分布参数，具体步骤如下。

（1）计算随机变量tmn样本数据的均值和方差，再计算变异系数，如公式⑵所示。

式中：c2为故障处理时间变异系数（c2中2表示平方）；VAR（tmn）为故障处理时间样本方差；E-（tmn）为故障处理时间样本均值。

（2）当c2≤1时，，[ ]为四舍五入取整符号，α= （1，0，…，0）1×Q，矩阵R为

（3）当c2＞ 1时，Q= 2，α= （p，1 -p），p=，矩阵R为

（4）根据矩阵R的不同取值，计算tmn最终 取值。

2 车辆检修排班计划优化模型及求解

2.1 构建排班计划优化模型

从企业的角度出发，以提高工作效率为目标，即故障处理时间最少；从员工的角度出发，期望各工班组工作时间尽量均衡。综合企业与员工要求确定目标，以一个月排班计划时间为最小单位，构建排班优化模型。

公式 ⑹ 为企业目标函数，表示所有工班组故障处理时间总和最小；公式 ⑺ 和公式 ⑻ 分别表示列检和均衡修工班组间工作量尽量平衡目标，用方差最小来表示。公式 ⑼ 至公式 ⑿ 为企业相关要求约束，其中公式 ⑼ 表示1个工作日内白班和夜班只有1个列检工班组当班，I为排班天数；公式⑽ 表示均衡修和专项修至少有1个在白班当班，但上限不超过3个；公式 ⑾ 表示均衡修和专项修不安排夜班；公式 ⑿ 表示所有工班组连续休息时间不超过2个工作日。公式 ⒀ 至公式 ⒄ 为员工休息时间保证约束，其中公式 ⒀ 表示不允许列检白班和夜班连续工作；公式 ⒁ 表示列检工班组的工作时间范围；公式 ⒂ 表示均衡修或专项修工班组的工作时间范围；公式 ⒃ 表示列检上完夜班后需要连续休息2个工作日；公式⒄表示如果工班组连续工作5个白班需要连续休息2个工作日。公式 ⒅ 至公式 ⒇ 为修程类别约束，其中公式 ⒅ 表示将列检修程中发生的故障安排给列检工班组；公式 ⒆ 表示将均衡修修程中发生的故障安排给均衡修工班组；公式 ⒇ 表示将专项修修程中发生的故障安排给专项修工班组。在以上模型中xijm，yijnk和zijmn为决策变量，其中xijm为0-1决策变量，当xijm= 1时表示指派班组m在第i个工作日时段j当班，否则xijm= 0；yijnk和zijmn取值范围均为正整数。

根据公式 ⑹ 至公式 ⒇ 构建的模型为多目标非线性混合整数规划模型[9]，需要将多目标转化为单目标整数规划问题求解。考虑到G1的量纲为时间，而G2和G3的量纲为时间的平方，因而将G2和G3转化为均方差表示来统一3个目标函数的量纲，考虑各目标权重关系得到总目标为G=ω1G1+ω2G2+ω3G3，其中ω1+ω2+ω3= 1；转化后的模型为单目标非线性混合整数规划模型，能够直接进行求解，输出排班计划决策变量xijm和zijmn。

2.2 模型验证

2.2.1 基础数据

以重庆地铁6号线智能运维系统采集的2019年12月1日至2020年12月31日共396 d数据为基础，经统计发现此时间段车辆检修10个子系统中处理故障种类168种，系统和故障分类统计如表1所示。为了计算和验证方便，将396天数据分为2部分：一部分为训练数据，时间范围为2019年12月1日至2020年11月30日，共365 d；另一部分为测试数据，时间范围为2020年12月1日至2020年12月31日，共31 d。利用相位分布均值方法计算，安全辅助设备系统故障处理时间统计结果如表2所示，车门系统故障处理时间统计结果如表3所示，车体结构系统故障处理时间统计结果如表4所示。限于篇幅其他数据未列出。

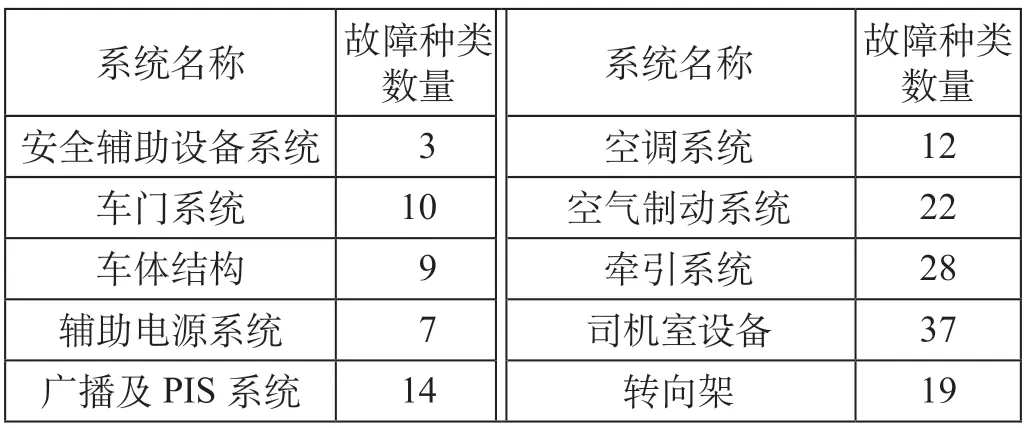
表1 系统和故障分类统计 个Tab.1 System and fault classification

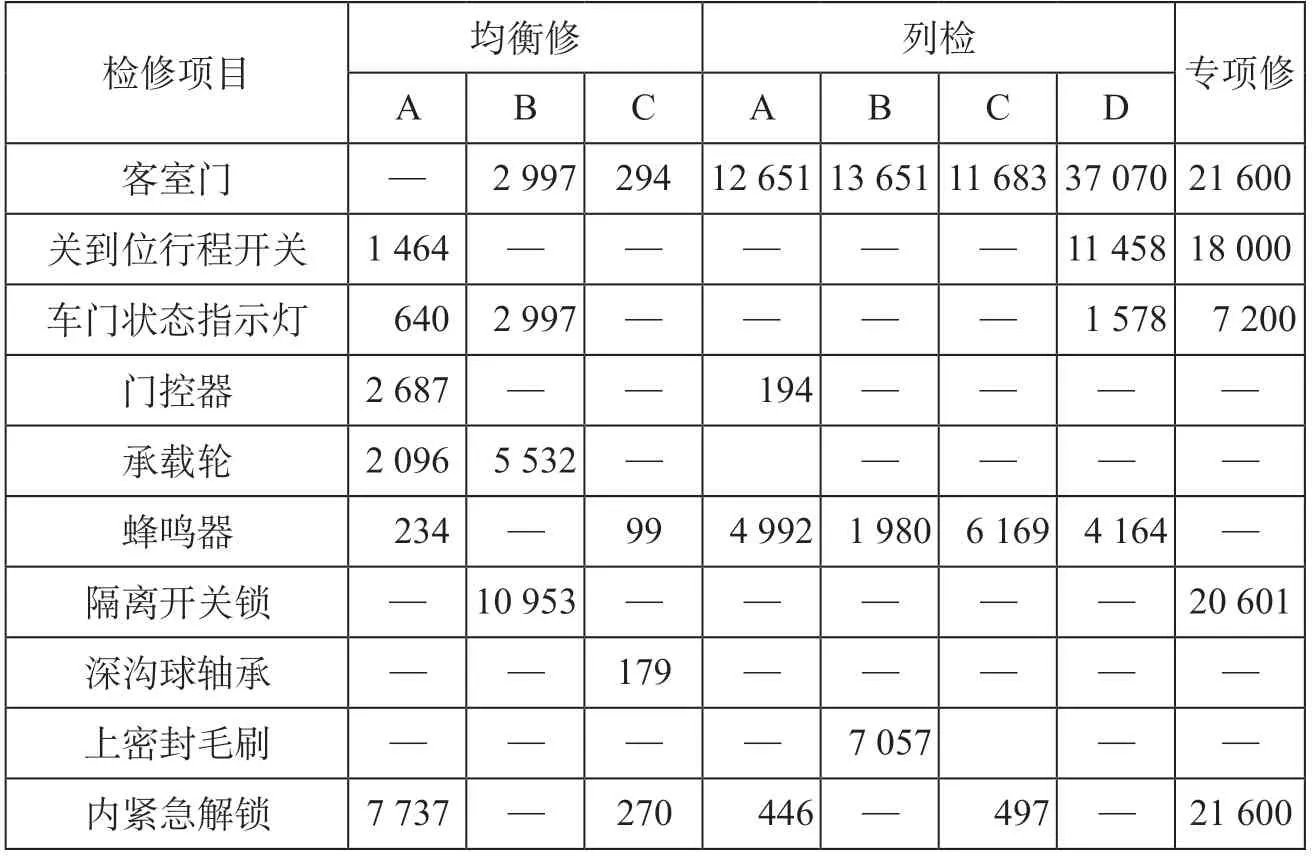
表3 车门系统故障处理时间统计结果 sTab.3 Statistical results of fault handling time of door system

由表2至表4可知，在历史数据记录中各工班组只处理过部分故障，以车门系统“关到位行程开关故障”为例，在数据中只有均衡修A班、列检D班和专项修工班处理过该故障，其他工班组没有处理过，因而数据为空，这种处理方式不会对模型计算准确性产生影响。

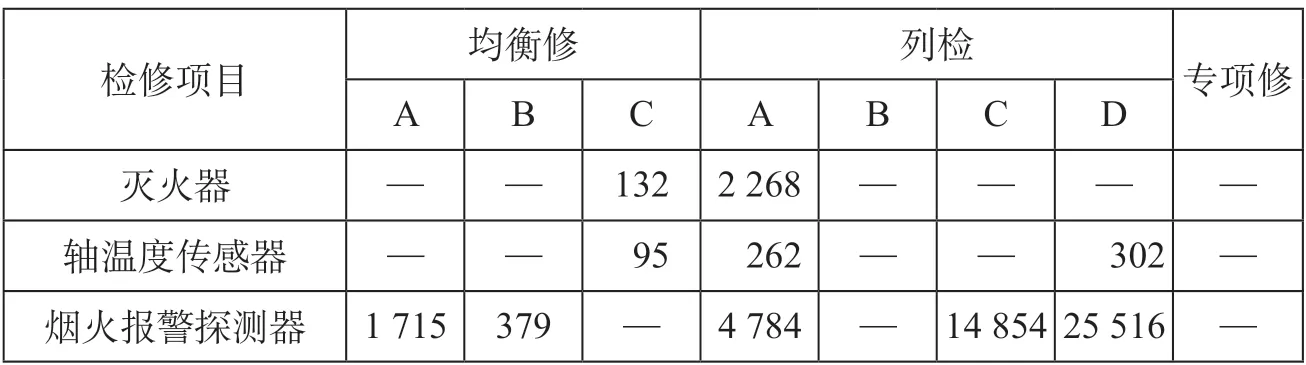
表2 安全辅助设备系统故障处理时间统计结果 sTab.2 Statistical results of fault handling time of auxiliary equipment system for safety

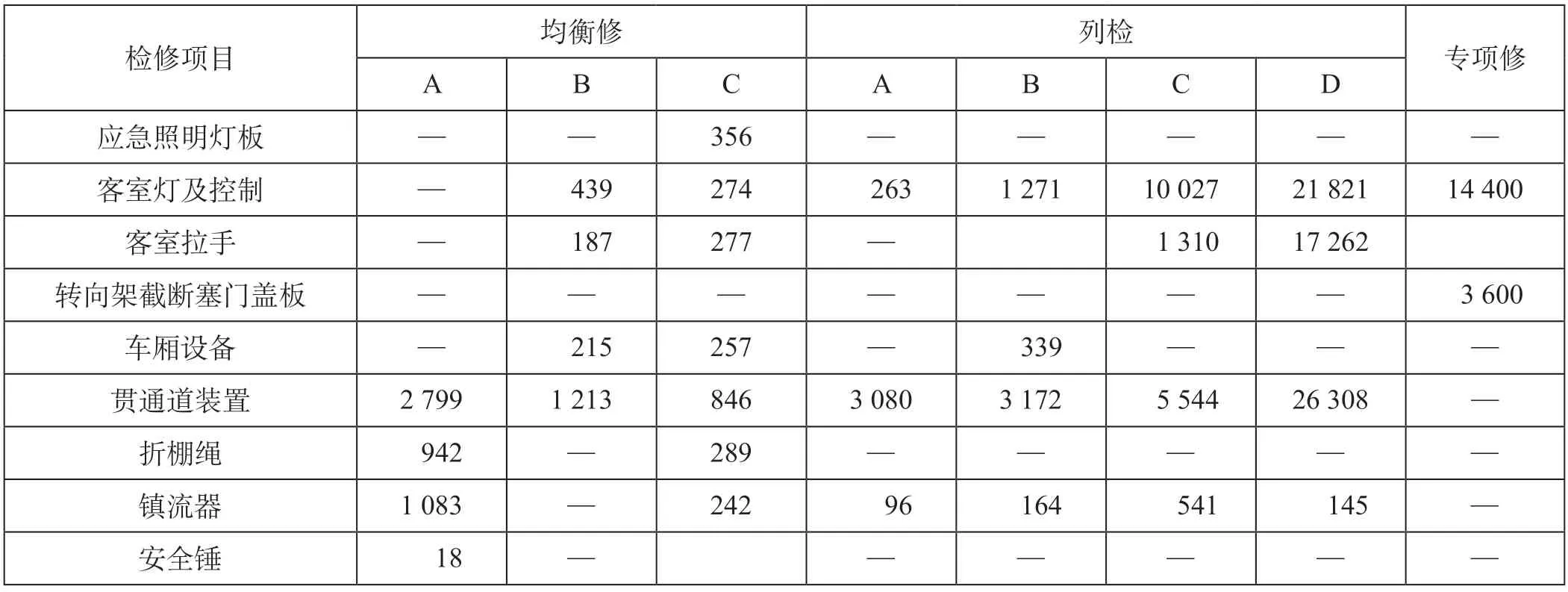
表4 车体结构系统故障处理时间统计结果 sTab.4 Statistical results of fault handling time of vehicle structure system

2.2.2 结果验证

将根据基础数据统计和计算得到的tmn和yijnk数值代入排班优化模型，取ω1= 0.6，ω2=ω3= 0.2。通过编程求解可得到2020年12月份排班计划表[10-12]。 对结果进行统计分析，列检A班、B班、C班、D班，均衡修A班、B班、C班和专项修工班组在1个月内上班时间分别为15 d，15 d，16 d，16 d，21 d，22 d，21 d，21 d。对于列检工班而言，白班和夜班的情况为列检A班有8个白班和7个夜班，列检B班有7个白班和8个夜班，列检C班有7个白班和9个夜班，列检D班有9个白班和7个夜班，白班和夜班的数量基本平衡。

优化前后工班组故障处理时间对比如表5所示，结果显示，列检4个工班进行优化后，列检A班、B班时间增加，C班、D班时间减少，说明新的排班计划将列检C班、D班部分故障处理任务安排给了效率更高的A班、B班。均衡修的3个工班情况为均衡修C班的大多数任务安排给了A班、B班。由于专项修只有1个工班组，因而时间不变。优化前后目标函数数值对比如表6所示，结果显示，对于目标1，优化后比优化前故障处理总时间降低了36.63%，优化效果明显。对于目标2，列检4个工班组优化前后故障处理时间均衡性提高了286%。对于目标3，均衡修3个工班组优化前后故障处理均衡性提高了119%，2类工班组间故障处理时间均衡性均有提高。总目标优化后比优化前提高了40%。

表5 优化前后工班组故障处理时间对比 sTab.5 Comparison of fault handling time before and after optimization

表6 优化前后目标函数数值对比 sTab.6 Numerical comparison of objective function before and after optimization

3 结束语

通过调整排班计划降低故障处理总时长，进而提高地铁车辆维修效率是一种行之有效的方法。利用足够的车辆检修数据，通过模型的计算能够发现检修薄弱环节，优化配置工班组资源。此外，还需要进一步加强维修作业标准化力度和先进维修技术的投入。下一步的研究工作主要有2方面：一是对故障预测技术做更加深入研究，从而提高车辆智能运维系统故障预测精度，使排班计划更准确；二是进一步深入研究求解大规模问题的算法，以期应对由城市轨道交通规模的扩大和工班组数量的增加，所造成的模型求解时间呈指数级增长带来的问题。