货车车辆段调车模型与求解

邱建东，任 伟，祁育栋，张 飞

（兰州交通大学 机电工程学院，甘肃 兰州 730070）

0 引言

货车车辆段主要承担铁路货车的段修任务，在整个段修过程中，调车作业是车辆段组织货车检修工作的关键步骤，也是比较复杂的作业内容。目前在实际的调车作业中，依旧采用人工或半人工作业方式，在车辆段检修能力及场地规模有限的前提下，随着货车检修数量增加，调车作业亦越来越复杂。因此，利用计算机编制和优化调车作业计划是一个亟需解决的理论和技术难题[1-2]。

许多学者将研究的重点投入到高速铁路动车所客车调车作业中，而铁路货车在进行检修作业时同样需要大量甚至更多的调车。动车所的调车作业跟货车车辆段的调车作业有相似之处。王忠凯等[3]将调车作业视作是有时空约束条件的车间调度问题，并以减少动车无效占用时间和调车路径费用为目标，利用改进的MAX-MIN蚁群系统求解；张惟皎等[4]考虑列位条件，目的在于提高存车线利用率和减少调车走行距离，并基于极大存车线方案，设计模拟退火算法并取得良好效果；王家喜[5]则以调车钩数最小为目标，优化调车钩数以提高调车效率，并设计粒子群算法对构建的整数模型求解；童佳楠等[6]在考虑列位约束条件的基础上，将调车作业视作是具有约束性质工艺的混合flow-shop调度问题，提出利用遗传算法解决该问题；殷迪等[7]则将调车作业视为带有不定加工时长的job-shop调度问题，以实现存车线上的总预留时间最大化，构建调车作业计划优化模型，利用启发式算法求解 模型。

在铁路车辆检修调车作业的研究中，无论是从问题自身出发，还是将问题转化为其他形式的问题，对于车辆在检修工序的顺序要求上都没有进行考虑，对于铁路货车而言，由于必要的检修步骤具有严格的顺序要求，这个问题也更加突出。因此，从这个角度出发，以货车线路占用时间及车辆转线时间和最小为目标构建模型，并运用改进的遗传算法求解。

1 车辆段线区布局

车辆段货车检修作业可视作一个整体，包括出入段作业和检修计划规定的若干项检修作业。各部分检修作业均需一定的时间完成，检修作业在具备条件的检修区内进行，货车在车辆段转线和停留，须满足股道与股道之间的连通和空间占用条件。

以兰州西车辆段段内线路布置为例，说明货车车辆段的功能分区，大部分车辆段只进行段修，少数车辆段在设备及场地条件允许的情况下会分担一部分站修任务。兰州西车辆段段内布局如图1所示，该车辆段内布置多个功能线区，其中D1—D4为段 修作业区，主要完成货车段修作业任务；Z1—Z3为 站修作业区，主要完成货车站修任务；T为调梁区，主要功能是为货车调梁；X为罐车清洗作业区，主要是在罐车检修前对其进行清洗作业，避免有毒、易燃、易爆气体或液体残留；P为抛丸、喷漆作业区，主要是进行货车车厢的抛丸、喷漆作业；R为预修作业区，主要对进入车辆段的所有货车进行预修作业；S1—S7为存车区，主要进行货车在段内的 中转、停留和整备等作业；E为车辆段进出线。

2 货车车辆段调车模型及求解

货车车辆段的调车作业基本包括所有货车在段内有向移动的全部内容，是将货车检修任务和车辆段检修资源调动起来的关键所在。

2.1 货车车辆段调车模型

2.1.1 模型建立

根据我国货车车辆段实际情况，货车的检修调车作业均依靠调车机车牵引完成，大多数车辆段仅配置2台牵引机车，日常调车作业中只运用1台机车，另1台为备用机车，因而调车机车的数量对模型的建立与求解不会造成冲突，调车方案的建立均以1台牵引机车为准。车辆段为实现检修效率的提高，根据检修计划及车辆段各个检修作业区检修台位的数量要求，同一类型检修项目的货车被推送至检修作业区进行同一作业，如兰州西车辆段段修作业区设有4条检修股道，每条检修股道可容纳7辆货车同时进行同一作业。建立模型时，由于同一类型检修项目的货车由调车机车一次性推入，检修完毕之后，由调车机车一次性牵出，可将这类货车视作一个整体。检修结束之后，货车将被牵引至存车线，次日成批交付。考虑到以上因素，在车辆段检修作业符合《铁路技术管理规程》及各检修规程的前提下，以货车检修时占线时间及车辆转线时间和Z最小为目标，建立以下调车作业模型。

式中：T为货车检修作业时间，h；F为调车作业中货车转线时间，h；e为车辆段内任意检修车辆；d为检修线区编号；l为检修线区内股道编号；D为车辆段线区集合；E为货车集合；W为转线路径集合；Ld为股道集合；m1，m2为分别表示T和F的权重系数，根据车辆段调车作业设备的配置情况，m1，m2的取值也不同，但都满足两者之和为1；xedl为 0-1变量，货车e在任意线区d的股道l上停留并进行检修作业为1，否则为0；为0-1变量，表示货车转线路径选择，当任意货车e按照其转线顺序，从线区d的股道l上转至另一检修线区d′的股道h上，选择W中的第k条调车路径时，为1，否则为0；为任意货车e进入线区d的股道l的时刻；为任意货车e离开线区d的l股道的时刻。

2.1.2 初始条件

（1）检修作业约束：如果货车需要在某线区进行检修作业，指定车辆须在指定线区选择一条股道进行停留，完成计划作业。

（2）路径约束：货车在两线区之间转线时只能选一条通路。

（3）检修作业时间约束：货车在指定股道检修作业时，必须在规定的时间内完成，否则视为不可检修，须离开检修股道。

式中：Te为货车检修最小用时，h。

（4）股道相容性约束：当某一股道上有货车进行检修作业或占用时，该股道不可停靠2辆及以上货车。

式中：zdlec为0-1变量，表示货车在股道的占用次序，当任意货车e优先货车c至股道l时，zdlec为1，否则为0；xcdl为0-1变量，表示任意货车c在任意线区d的股道l上停留并进行检修作业为1，否则为0。

2.2 模型求解

2.2.1 遗传算法

货车车辆段检修调车作业是一个NP-hard问题，这类问题随着车辆段检修货车、检修股道数量及检修作业工序的增加，其组合量会以指数级增加，很难用传统的数学规划方法从其中找到最优解。遗传算法在解决调度问题时，其优势在于一方面可以随机从一个目标转向下一个目标，不易陷入局部搜索的困境之中，另一方面搜索时具有较高效率，通过以下设置以实现对模型的求解[8]。

（1）编码设计。将货车需要进行的若干项检修项目视为具有遗传性质的染色体，并且将其分配到不同股道，研究采用自然数向量表示的编码方式，将货车需要进行的检修项目进行自然数排列，向量τ= {r1，r2，…，rn}代表一个完整检修作业，从r1到r2，…，rn-1到rn，再从rn返回到r1。例 如，向 量τ为{1，2，3，4，5，6，7，8，9，10}的排列，表示一个完整的检修作业集合有10个工序，则对于集合R= {1，2，3，4，5，6，7，8，9，10}，如果有一个体的向量为{5，4，9，10，8，1，2，7，6，3}，则表示的检修顺序为5→4→9→10→8→1→2→7→6→3→5。

（2）适应度函数。在遗传算法中，依靠适应度函数值来衡量群体中个体适应环境的能力，适应度函数通常是由目标函数转换而成，函数值越大的个体将有机会获得更大的机会繁衍下一代。根据调车作业优化模型，货车占线及转线的时间越大，则表明所产生的方案越不理想，也就意味着被淘汰的可能性越大。由目标函数变换得到的适应度函数计算公式为

式中：Ti表示进行第i道检修工序的最小检修时间，h；Fi表示转线至第i道检修工序所在股道的最小时间，h。

（3）选择。研究采用随机竞争选择方式，假设群体大小为Ni，首先采用轮盘赌的形式选择1对个体i，j，则任意个体i的适应度为fi，j的适应度为fj，然后2个个体间进行竞争，适应度值高的被选中，如此反复操作直到选满，个体被首先选中的概率为

（4）遗传操作。在整个遗传算法的运算过程中，遗传操作是其中重要的步骤之一，交叉运算将遗传算法跟其他的元启发式算法区别开来，是遗传算法中关键之处，是产生新个体的主要方法。研究中采用比较广泛的两点交叉，两点交叉运算示意图如图2所示。

①将生成的新个体融入下一代形成新的种群，并判断新种群的规模，如果达不到初始种群的规模，则重复交叉操作直至达到要求，然后终止交叉操作。交叉概率Pc拟给定为0.9。

②变异采用启发式变异方法。随机产生2个变异位置i和j，交换位置i和j上的基因。变异概率Pm拟给定为0.08。启发式变异示意图如图3所示。

（5）算法终止。设置迭代次数，达到最大次数时运算结束并输出结果。

2.2.2 算法求解

求解步骤如下。

步骤1：依据货车参数信息，分析货车故障类型并制定合理检修计划。

步骤2：算法相关参数设置。

步骤3：利用合理的编码形式将实际问题转换，并且生成初始种群。

步骤4：设计适应度函数，利用遗传操作过程选取适应度比较高的个体，并且遗传给下一代。

步骤5：求最优解至符合遗传终止条件。

步骤6：输出最优结果并进行分析。

3 实例分析

为了验证研究提出的考虑货车检修顺序的情况及模型的有效性，以兰州西车辆段实际检修作业为例，对其调车作业进行分析，以该车辆段日常检修的敞车、平车、棚车、罐车4种车型作为检修实例，并根据实际作业数据对模型进行解算。

（1）各车型检修作业占线时间如表1所示。

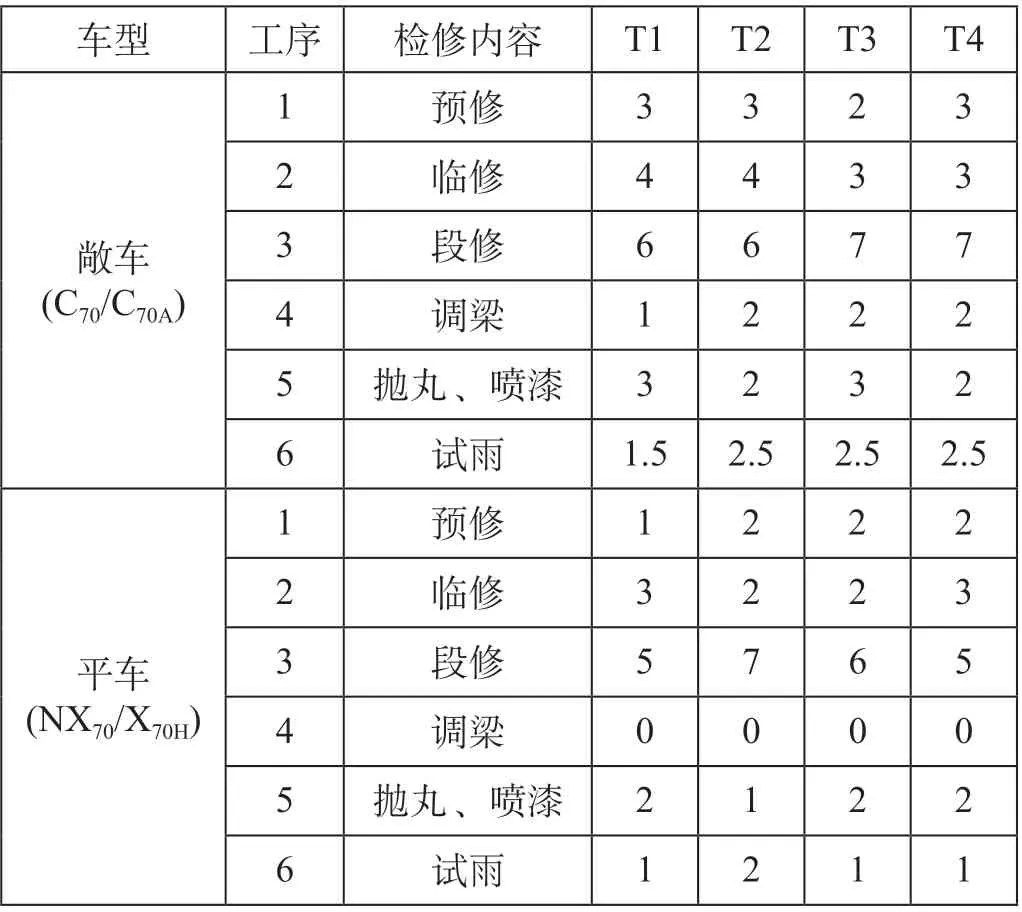
表1 检修作业占线时间 hTab.1 Busy time of maintenance operation

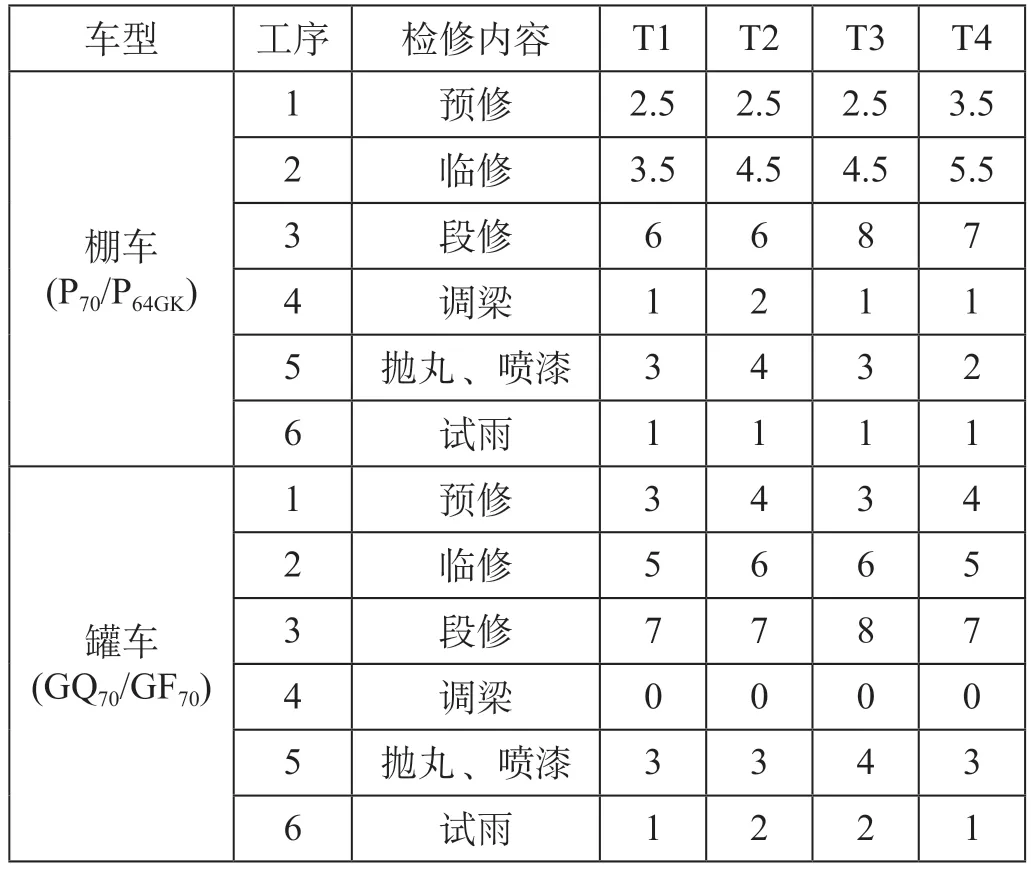
续表

（2）货车检修转线时间如表2所示。

表2 检修转线时间表 hTab.2 Maintenance transfer schedule

（3）遗传参数设置如表3所示。

表3 遗传参数设置Tab.3 Genetic parameter setting

设计编码形式为4×6 = 24 bit，随机选取4辆车的父代染色体 （1 1 5 3 4，2 2 6 5 1，2 1 3 3 6 4 ，1 3 4 5 2 1），每条染色体上的编码字符顺序从左至右依次表示货车检修项目所在股道号排列，字符本身表示各检修项目下工序序号。例如，第一染色体（1 1 5 3 4）中“5”表示该敞车执行第5道检修工序时在第3股道；“3”则表示该敞车执行第3道检修工序时在第4股道。相应地，第2、第3、第4条染色体依次表示平车、棚车、罐车，其字符串含义同上。取m1为0.4，m2为0.6，经编程实现选择、交叉、变异和筛选，算法求解完成，目标函数收敛图如图4所示。由图4可以看出，当迭代次数达到 48次时得到最优解（3 3 2 3 3 1，4 3 1 0 2 6，2 2 2 3 4 1，4 4 1 0 2 4），其中“0”表示该类车型不进行此项检修作业。对应的得到目标函数值为27.64 h， 占用总时间为65.5 h，调车时间为2.4 h，小于车辆段规定维修时间72 h。每道工序在相应股道进行检修作业甘特图如图5所示。同样，在迭代至48次时，适应度函数呈收敛状态，适应度收敛图如图6所示。由此可以看出遗传算法实现了检修时间及转线时间的缩减，在一定意义上实现了优化的目的，为货车调车作业实现自动化提供了理论帮助。

4 结论

根据现行车辆段货车检修制度及车辆段调车作业的特点，在货车检修数量逐年增长、车辆段调车作业日益复杂、调车作业计划编制水平低下的背景下，提高货车车辆段调车作业质量及实际检修能力具有重要意义。考虑到车辆段货车检修台位及股道利用，建立货车车辆段调车作业优化模型，并设计基于货车检修作业顺序的改进遗传算法进行求解，结合兰州西车辆段实例对其进行验证，得到以下结论。

（1）通过遗传算法的反复迭代，进而逐步获得问题的优化解，与目前车辆段采取的人工调度方式相比，可以充分地考虑到货车检修台位及调车股道的适用性，进而提高车辆段检修效率。

（2）合理地考虑车辆段车辆检修作业顺序，可以提高调车作业计划的编制质量。

针对不同类型的货车车辆段，调车计划是保证调车作业的具体行动计划，不仅仅要保证其质量，计划编制的效率也是关键，调车计划编制方法将是下一步研究的方向。